数学建模算法汇总(全网最全,含matlab案例代码)
数学建模常用的算法分类
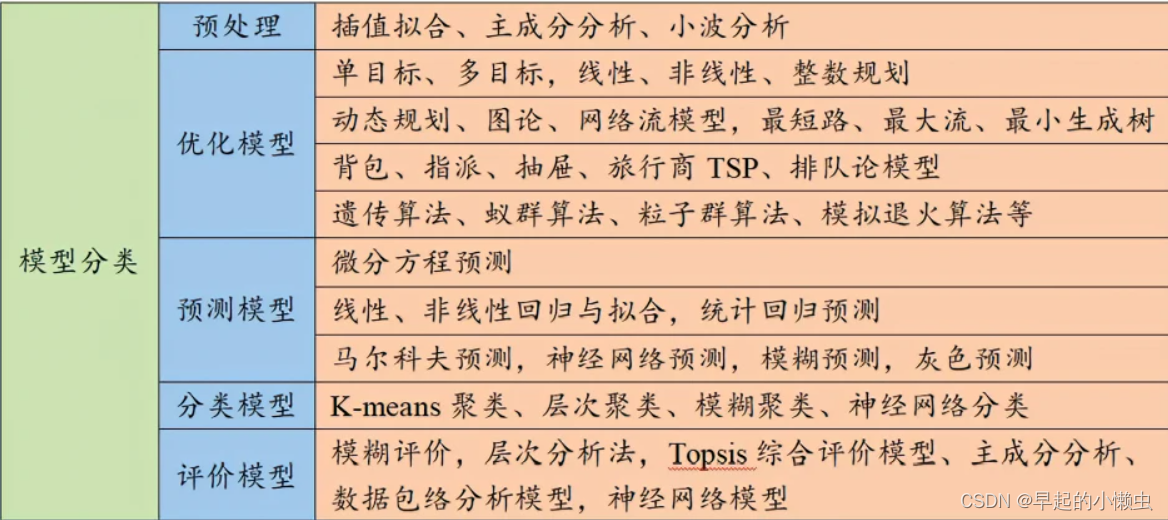
全国大学生数学建模竞赛中,常见的算法模型有以下30种:
- 最小二乘法
- 数值分析方法
- 图论算法
- 线性规划
- 整数规划
- 动态规划
- 贪心算法
- 分支定界法
- 蒙特卡洛方法
- 随机游走算法
- 遗传算法
- 粒子群算法
- 神经网络算法
- 人工智能算法
- 模糊数学
- 时间序列分析
- 马尔可夫链
- 决策树
- 支持向量机
- 朴素贝叶斯算法
- KNN算法
- AdaBoost算法
- 集成学习算法
- 梯度下降算法
- 主成分分析
- 回归分析
- 聚类分析
- 关联分析
- 非线性优化
- 深度学习算法
一、线性回归:用于预测一个连续的输出变量。
线性回归是一种基本的统计学方法,用于建立一个自变量(或多个自变量)和一个因变量之间的线性关系模型,以预测一个连续的输出变量。这个模型的形式可以表示为:
y = β0 + β1x1 + β2x2 + ... + βpxp + ε
其中,y 是因变量(也称为响应变量),x1, x2, ..., xp 是自变量(也称为特征变量),β0, β1, β2, ..., βp 是线性回归模型的系数,ε 是误差项
线性回归的目标是找到最优的系数 β0, β1, β2, ..., βp,使得模型预测的值与真实值之间的误差最小。这个误差通常用残差平方和来表示:
RSS = Σ (yi - ŷi)^2
其中,yi 是真实的因变量值,ŷi 是通过线性回归模型预测的因变量值。线性回归模型的最小二乘估计法就是要找到一组系数,使得残差平方和最小。
线性回归可以通过多种方法来求解,其中最常用的方法是最小二乘法。最小二乘法就是要找到一组系数,使得残差平方和最小。最小二乘法可以通过矩阵运算来实现,具体地,系数的解可以表示为:
β = (X'X)^(-1)X'y
其中,X 是自变量的矩阵,包括一个截距项和所有自变量的值,y 是因变量的向量。
线性回归在实际中的应用非常广泛,比如在金融、医学、工程、社会科学等领域中,都可以使用线性回归来预测和分析数据。
下面是一个简单的 Python 代码实现线性回归
import numpy as np
from sklearn.linear_model import LinearRegression# 创建一个随机数据集
np.random.seed(0)
X = np.random.rand(100, 1)
y = 2 + 3 * X + np.random.rand(100, 1)# 创建线性回归模型并拟合数据
model = LinearRegression()
model.fit(X, y)# 打印模型的系数和截距项
print('Coefficients:', model.coef_)
print('Intercept:', model.intercept_)# 预测新数据
X_new = np.array([[0.5], [1.0]])
y_new = model.predict(X_new)# 打印预测结果
print('Predictions:', y_new)
这个代码使用了 Numpy 库生成了一个包含 100 个样本的随机数据集,并使用 Scikit-learn 库的 LinearRegression 类创建了一个线性回归模型。模型通过 fit() 方法拟合数据,并通过 coef_ 和 intercept_ 属性访问模型的系数和截距项。最后,代码使用 predict() 方法预测了两个新数据点的结果,并打印出了预测结果。
二、逻辑回归:用于预测一个离散的输出变量,比如二元分类问题。
逻辑回归是一种常见的分类算法,用于将一个或多个自变量与一个二元或多元离散的因变量之间的关系建模。它的名字"逻辑"来源于它的模型本质上是一个逻辑函数,用于将输入值转换为一个概率值。逻辑回归通常用于二元分类问题,但也可以扩展到多元分类问题。
逻辑回归模型的基本形式如下:
p(y=1|x) = 1 / (1 + exp(-(b0 + b1x1 + b2x2 + ... + bpxp)))
其中,p(y=1|x) 是给定自变量 x 下因变量 y 取值为 1 的概率,exp() 是指数函数,b0, b1, b2, ..., bp 是模型的系数。
逻辑回归的目标是找到最优的系数 b0, b1, b2, ..., bp,以最大化似然函数,从而使模型预测的结果尽可能地接近真实值。通常,我们会使用极大似然估计法来估计模型的系数。
在训练过程中,逻辑回归模型使用一个称为逻辑损失函数的代价函数来衡量预测结果与真实值之间的误差。逻辑损失函数如下:
J(b) = (-1/m) * Σ[yi*log(p(xi)) + (1-yi)*log(1-p(xi))]
其中,m 是样本数量,yi 是真实的分类标签(0 或 1),p(xi) 是模型预测的分类概率。
逻辑回归可以使用梯度下降法或牛顿法等优化算法来最小化逻辑损失函数,从而得到最优的模型参数。最后,模型将自变量输入到逻辑函数中,得到分类概率,并使用阈值将概率转化为分类标签,通常取阈值为 0.5。
逻辑回归在实际中的应用非常广泛,比如在金融、医学、社会科学等领域中,都可以使用逻辑回归来预测和分析数据。
下面是一个简单的 Python 代码实现逻辑回归:
import numpy as np
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 创建一个随机数据集
np.random.seed(0)
X = np.random.rand(100, 3)
y = np.random.randint(0, 2, 100)# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)# 创建逻辑回归模型并拟合数据
model = LogisticRegression()
model.fit(X_train, y_train)# 预测测试集的结果
y_pred = model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print('Accuracy:', accuracy)
这个代码使用了 Numpy 库生成了一个包含 100 个样本的随机数据集,并使用 Scikit-learn 库的 LogisticRegression 类创建了一个逻辑回归模型。模型通过 fit() 方法拟合数据,并通过 predict() 方法预测测试集的结果。最后,代码使用 accuracy_score() 方法计算模型的准确率,并打印出结果。
三、决策树:用于分类和回归问题,通过构建一个树状结构来做出决策。
决策树是一种常见的机器学习算法,用于解决分类和回归问题。它的基本思想是将数据集分成多个子集,每个子集对应一个决策树节点,最终形成一棵树形结构。决策树的每个节点表示一个特征,分支表示特征的取值,叶子节点表示分类或回归的结果。
决策树的构建过程一般分为两个阶段:树的生成和剪枝。树的生成过程是从根节点开始,依次选择最优的特征进行划分,直到所有叶子节点都属于同一类别或满足某个停止条件。最常用的特征选择方法是信息增益或信息增益比。信息增益是指在划分前后,数据集中不确定性减少的程度,信息增益越大,意味着特征对于分类的影响越大。
剪枝过程是为了避免过拟合,即在训练集上表现良好但在测试集上表现差的情况。剪枝的目的是去除一些决策树节点,从而使决策树更加简单、泛化能力更强。剪枝方法通常包括预剪枝和后剪枝。预剪枝是在树的生成过程中,当某个节点无法继续划分时,停止划分。后剪枝是在树的生成过程结束后,对生成的树进行剪枝。剪枝的具体方法包括交叉验证剪枝和错误率降低剪枝等。
决策树在分类和回归问题中都有广泛的应用,它的优点包括易于理解和解释、处理缺失数据、对异常值不敏感、适用于多分类和回归问题等。但是决策树也有一些缺点,如容易过拟合、对输入数据的细微变化敏感等。
以下是一个示例代码,使用 Scikit-learn 库中的 DecisionTreeClassifier 类构建并训练一个决策树分类器:
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split# 载入数据集
iris = load_iris()# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)# 创建决策树分类器并拟合数据
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)# 预测测试集的结果
y_pred =
在此示例中,我们使用 Iris 数据集,将数据集分为训练集和测试集
四、支持向量机:用于分类和回归问题,通过找到一个最优的分离超平面来进行分类。
支持向量机(Support Vector Machine,简称 SVM)是一种常用的监督学习算法,常用于分类和回归问题。SVM 基于将数据映射到高维空间,并在该空间中寻找最大间隔超平面来进行分类或回归。
SVM 的目标是找到一个最大间隔超平面,它将不同类别的数据分开,使得同一类别的数据点尽可能地靠近这个超平面。具体来说,对于二分类问题,SVM 将数据映射到高维空间,并找到一个超平面,它能够将两类数据分开,并且距离两类数据点最近的点到该超平面的距离最大。
在实现 SVM 时,需要选择一个核函数来对数据进行映射,常用的核函数有线性核、多项式核和径向基函数(Radial Basis Function,简称 RBF)核等。
下面是一个使用 Scikit-learn 库中的 SVM 类(SVC)实现分类问题的示例代码:
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split# 载入数据集
iris = load_iris()# 划分数据集为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=42)# 创建 SVM 分类器并拟合数据
clf = SVC(kernel='linear', C=1.0, random_state=42)
clf.fit(X_train, y_train)# 预测测试集的结果
y_pred = clf.predict(X_test)# 计算分类器在测试集上的准确率
accuracy = clf.score(X_test, y_test)
print("Accuracy: {:.2f}%".format(accuracy*100))
五、聚类:用于将数据集中的数据分为不同的组。
聚类是一种无监督学习算法,用于将数据集中的对象分成几个相似的组或类别。聚类算法的目标是找到一些相似的数据点,并将它们分成不同的类别或簇,使得同一类别的数据点尽可能地相似,而不同类别的数据点尽可能地不同。
常见的聚类算法包括 K-Means 算法、层次聚类算法和 DBSCAN 算法等。其中,K-Means 算法是最常见的聚类算法之一,它将数据点分为 K 个簇,并将每个数据点分配到最近的簇中,
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans# 生成模拟数据
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)# 创建 KMeans 聚类器并拟合数据
kmeans = KMeans(n_clusters=4, random_state=0)
kmeans.fit(X)# 预测数据的簇标签
y_pred = kmeans.predict(X)# 绘制聚类结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5);
六、神经网络:用于分类和回归问题,通过构建一个多层的神经网络来进行计算。
神经网络是一种模仿人类大脑神经网络结构和工作方式的算法模型。它由许多简单的单元或神经元组成,每个神经元接收来自其它神经元的输入,并将这些输入组合成一个输出。神经网络通常由多个层组成,包括输入层、隐藏层和输出层,每层由若干个神经元组成。
神经网络可以用于分类、回归和聚类等任务,其中最常见的是分类任务。神经网络分类器的训练通常采用反向传播算法,它通过计算误差梯度来更新神经网络权重,以使神经网络的输出尽可能接近真实标签。
以下是一个使用 Scikit-learn 库中的 MLPClassifier 类实现分类问题的示例代码:
from sklearn.datasets import make_classification
from sklearn.neural_network import MLPClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 生成模拟数据
X, y = make_classification(n_samples=1000, n_features=10, n_classes=2, random_state=1)# 将数据集划分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)# 创建 MLPClassifier 分类器并拟合数据
mlp = MLPClassifier(hidden_layer_sizes=(10, 5), max_iter=1000, random_state=1)
mlp.fit(X_train, y_train)# 预测测试集的标签
y_pred = mlp.predict(X_test)# 计算分类器的准确率
acc = accuracy_score(y_test, y_pred)
print(f"Accuracy: {acc}")
七、遗传算法:用于寻找优化问题的最优解。
遗传算法是一种模仿自然选择和遗传机制的优化算法,主要用于求解最优化问题。它模拟了生物进化过程中的遗传、交叉和变异过程,通过不断地进化优秀的个体,逐渐搜索到全局最优解。
遗传算法的基本流程如下:
- 初始化种群:随机生成一组个体作为种群。
- 评价适应度:对每个个体进行适应度评价,通常使用目标函数计算个体的适应度。
- 选择操作:根据每个个体的适应度,选择一部分个体作为父代,用于产生下一代。
- 交叉操作:对父代个体进行交叉操作,产生新的个体。
- 变异操作:对新的个体进行变异操作,产生更多的多样性。
- 评价新个体:对新的个体进行适应度评价。
- 判断终止条件:如果满足终止条件,则输出最优解;否则返回第3步。
以下是一个使用 Python 实现遗传算法求解一元函数最小值问题的示例代码:
import random# 目标函数:f(x) = x^2
def objective_function(x):return x ** 2# 生成随机个体
def generate_individual():return random.uniform(-10, 10)# 计算个体适应度
def calculate_fitness(individual):return 1 / (1 + objective_function(individual))# 选择操作
def selection(population):fitnesses = [calculate_fitness(individual) for individual in population]total_fitness = sum(fitnesses)probabilities = [fitness / total_fitness for fitness in fitnesses]selected = random.choices(population, weights=probabilities, k=len(population))return selected# 交叉操作
def crossover(individual1, individual2):alpha = random.uniform(0, 1)new_individual1 = alpha * individual1 + (1 - alpha) * individual2new_individual2 = alpha * individual2 + (1 - alpha) * individual1return new_individual1, new_individual2# 变异操作
def mutation(individual):new_individual = individual + random.uniform(-1, 1)return new_individual# 遗传算法求解最小值问题
population_size = 100
population = [generate_individual() for i in range(population_size)]
num_generations = 1000
for generation in range(num_generations):# 选择操作selected_population = selection(population)# 交叉操作offspring_population = []for i in range(population_size):offspring1, offspring2 = crossover(selected_population[i], selected_population[(i+1) % population_size])offspring_population.append(offspring1)offspring_population.append(offspring2)# 变异操作for i in range(population_size):if random.uniform(0, 1) < 0.1:offspring_population[i] = mutation(offspring_population[i])#
八、粒子群算法:用于寻找优化问题的最优解。
粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,通过模拟群体中粒子的移动和群体的信息交流来实现优化目标的搜索。每个粒子在搜索空间中移动,并记录自己的最优位置和群体的最优位置,通过不断地调整自己的位置和速度,逐渐接近最优解。
粒子群算法的基本流程如下:
- 初始化粒子群:随机生成一组粒子的位置和速度。
- 计算适应度值:对每个粒子进行适应度计算,通常使用目标函数计算粒子的适应度。
- 更新个体最优值:将每个粒子的当前位置作为个体最优位置,如果该位置优于个体历史最优位置,则更新个体历史最优位置。
- 更新群体最优值:将所有粒子的个体最优位置作为群体最优位置。
- 更新速度和位置:根据粒子当前位置、速度和群体最优位置,计算新的速度和位置。
- 判断终止条件:如果满足终止条件,则输出最优解;否则返回第2步。
以下是一个使用 Python 实现粒子群算法求解一元函数最小值问题的示例代码:
import random# 目标函数:f(x) = x^2
def objective_function(x):return x ** 2# 生成随机粒子
def generate_particle():position = random.uniform(-10, 10)velocity = random.uniform(-1, 1)return {'position': position, 'velocity': velocity, 'personal_best_position': position, 'personal_best_fitness': objective_function(position)}# 更新个体最优值
def update_personal_best(particle):fitness = objective_function(particle['position'])if fitness < particle['personal_best_fitness']:particle['personal_best_position'] = particle['position']particle['personal_best_fitness'] = fitness# 更新群体最优值
def update_global_best(particles):global_best_position = particles[0]['personal_best_position']global_best_fitness = particles[0]['personal_best_fitness']for particle in particles:if particle['personal_best_fitness'] < global_best_fitness:global_best_position = particle['personal_best_position']global_best_fitness = particle['personal_best_fitness']return global_best_position, global_best_fitness# 更新速度和位置
def update_velocity_and_position(particle, global_best_position):w = 0.5 # 惯性权重c1 = 0.5 # 个体学习因子c2 = 0.5 # 群体学习因子r1 = random.uniform(0, 1)r2 = random.uniform(0, 1)new_velocity = w * particle['velocity'] + c1 * r1 * (particle['personal_best_position'] - particle['position']) + c2 * r2 * (global_best_position - particle['position'])new
九、蚁群算法:用于解决组合优化问题。
蚁群算法(Ant Colony Optimization,ACO)是一种模拟蚂蚁在寻找食物时的行为和信息交流的启发式优化算法。该算法通过模拟蚂蚁的觅食行为,以信息素作为引导信息,通过搜寻路径上信息素的累积来实现最优路径的搜索。
蚁群算法的基本流程如下:
- 初始化信息素:对每条路径初始化一定量的信息素。
- 初始化蚂蚁位置:随机分配蚂蚁的起点位置。
- 选择下一步位置:根据当前位置和信息素分布选择下一步的位置。
- 更新信息素:根据蚂蚁经过的路径更新信息素。
- 判断终止条件:如果满足终止条件,则输出最优解;否则返回第3步。
以下是一个使用 Python 实现蚁群算法求解旅行商问题(TSP)的示例代码
import random# 旅行商问题:求解城市之间的最短路径
class TSP:def __init__(self, num_cities, distance_matrix):self.num_cities = num_citiesself.distance_matrix = distance_matrix# 计算路径长度def path_length(self, path):length = 0for i in range(len(path)-1):length += self.distance_matrix[path[i]][path[i+1]]length += self.distance_matrix[path[-1]][path[0]]return length# 生成随机解def random_solution(self):path = list(range(self.num_cities))random.shuffle(path)return path# 蚂蚁类
class Ant:def __init__(self, tsp, alpha, beta, rho):self.tsp = tspself.alpha = alpha # 信息素重要程度因子self.beta = beta # 启发式因子self.rho = rho # 信息素挥发因子self.current_city = random.randint(0, tsp.num_cities-1) # 当前所在城市self.visited_cities = [self.current_city] # 已访问过的城市self.path_length = 0 # 路径长度# 选择下一步城市def choose_next_city(self, pheromone_matrix):unvisited_cities = list(set(range(self.tsp.num_cities)) - set(self.visited_cities))probabilities = [0] * len(unvisited_cities)total_pheromone = 0for i, city in enumerate(unvisited_cities):probabilities[i] = pheromone_matrix[self.current_city][city] ** self.alpha * ((1 / self.tsp.distance_matrix[self.current_city][city]) ** self.beta)total_pheromone += probabilities[i]if total_pheromone == 0:return random.choice(unvisited_cities)probabilities = [p / total_pheromone for p in probabilities]next_city = random.choices(unvisited_cities, weights=probabilities)[0]
十、模拟退火算法:用于在一个大的搜索空间中找到一个最优解。
模拟退火算法(Simulation Annealing,SA)是一种基于概率的全局优化算法,其灵感来源于固体材料在退火过程中的微观状态变化过程。该算法通过一定的概率接受一个劣解以避免陷入局部最优解,并在迭代过程中逐渐降低概率,最终达到全局最优解的目的。
模拟退火算法的基本流程如下:
- 初始化温度T、初始解x、终止温度Tmin和降温速率α。
- 迭代直至温度降至Tmin:在当前解x的邻域中随机生成一个新解y。
- 判断接受概率:计算当前解x和新解y的差值ΔE,如果ΔE<0,则接受新解y;否则以一定概率接受新解y,概率为e^(-ΔE/T)。
- 降温:通过降温速率α逐渐降低温度T。
- 返回第2步。
以下是一个使用 Python 实现模拟退火算法求解旅行商问题(TSP)的示例代码:
import math
import random# 旅行商问题:求解城市之间的最短路径
class TSP:def __init__(self, num_cities, distance_matrix):self.num_cities = num_citiesself.distance_matrix = distance_matrix# 计算路径长度def path_length(self, path):length = 0for i in range(len(path)-1):length += self.distance_matrix[path[i]][path[i+1]]length += self.distance_matrix[path[-1]][path[0]]return length# 生成随机解def random_solution(self):path = list(range(self.num_cities))random.shuffle(path)return path# 模拟退火类
class SimulatedAnnealing:def __init__(self, tsp, T, Tmin, alpha):self.tsp = tspself.T = T # 初始温度self.Tmin = Tmin # 终止温度self.alpha = alpha # 降温速率# 计算接受概率def acceptance_probability(self, old_cost, new_cost, T):if new_cost < old_cost:return 1else:return math.exp(-(new_cost - old_cost) / T)# 迭代求解def solve(self):current_solution = self.tsp.random_solution()current_cost = self.tsp.path_length(current_solution)while self.T > self.Tmin:new_solution = self.tsp.random_solution()new_cost = self.tsp.path_length(new_solution)if self.acceptance_probability(current_cost, new_cost, self.T) > random.random():current_solution = new_solutioncurrent_cost = new_costself.T *= self.alphareturn current_solution, current_cost
30+种算法模型及案例代码知识分享(纯干货):
链接:https://pan.baidu.com/s/1Pg_PgPJ8-EJ0RMjZ6_dF3Q?pwd=fid3
提取码:fid3
20+个matlab算法代码集合分享:
链接:https://pan.baidu.com/s/1HvGCIFK4zu5K3kZeJghy9A
提取码:ly5o
相关文章:

数学建模算法汇总(全网最全,含matlab案例代码)
数学建模常用的算法分类 全国大学生数学建模竞赛中,常见的算法模型有以下30种: 最小二乘法数值分析方法图论算法线性规划整数规划动态规划贪心算法分支定界法蒙特卡洛方法随机游走算法遗传算法粒子群算法神经网络算法人工智能算法模糊数学时间序列分析马…...
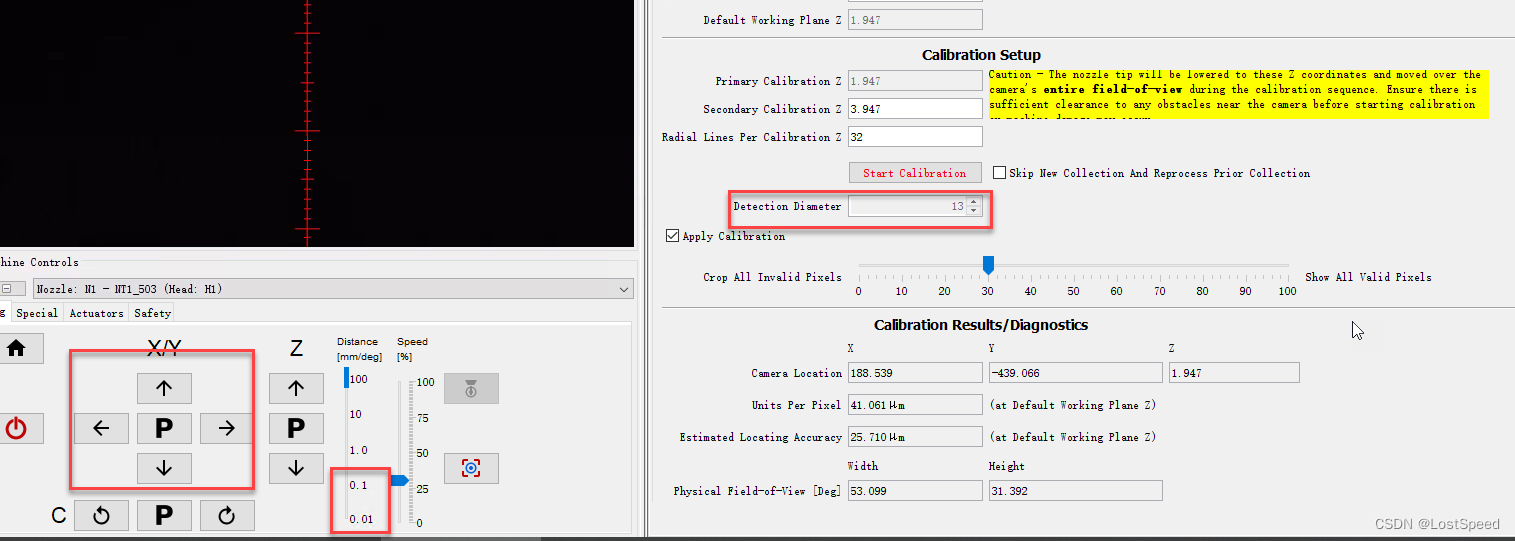
openpnp - 底部相机高级矫正后,底部相机看不清吸嘴的解决方法
文章目录 openpnp - 底部相机高级矫正后,底部相机看不清吸嘴的解决方法概述解决思路备注补充 - 新问题 - N1吸嘴到底部相机十字中心的位置差了很多END openpnp - 底部相机高级矫正后,底部相机看不清吸嘴的解决方法 概述 自从用openpnp后, 无论版本(dev/test), 都发现一个大概…...

怎么提高自己当众讲话的能力?
当众讲话是一项重要的沟通技能,它可以帮助你在各种场合中表达自己的观点、影响他人,并建立自信。虽然对很多人来说,当众讲话可能是一项挑战,但通过一些实践和技巧,你可以提高自己的当众讲话能力。下面是一些方法&#…...

孙哥Spring源码第20集
第20集 refresh()-invokeBeanFactoryPostProcessor 四-处理Configuration下的Bean生成代理对象 【视频来源于:B站up主孙帅suns Spring源码视频】【微信号:suns45】 1、二行InvokeBeanFactoryPostProcessors的作用 registryProcessors:处理的…...

【计算机网络】HTTP(上)
文章目录 1.HTTP概念2. URLurlencode 和 urldecode转义规则 3. HTTP的宏观理解HTTP的请求HTTP的响应 4. 见一见HTTP请求和响应请求报头 1. 模拟一个简单的响应response响应报头 2. 从路径中获取内容ReadFile函数的实现 3.不同资源进行区分反序列化的实现ReadOneLine函数的实现P…...
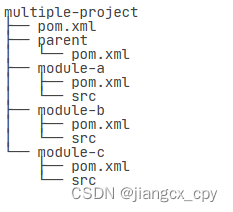
Maven学习记录
一、Maven是什么 简单来说Maven是一个标准化的java管理和构建工具,它提供了一系列规范,包括项目结构,构建流程(编译,测试,打包,发布……),依赖管理等。 标准化就是定下…...

H5游戏开发H5休闲小游戏定制H5软件定制
H5游戏是一种运行在网页浏览器中的HTML5技术开发的游戏。H5休闲小游戏通常具有简单的玩法,易于上手,适合快速的娱乐。以下是开发H5休闲小游戏的一般步骤: 1. 制定游戏开发概念: 确定H5游戏开发的主题和玩法。休闲小游戏通常应该…...
Spring基础及IoC容器的理解
Spring概念: 通常所说的Spring指的是Spring Framewprk(Spring框架),它是一个开源的框架。用一句话概括就是:Spring是包含了众多工具方法的IoC容器。 什么是容器? 容器是用来容纳某种物品的装置,在之前的学习中&…...

护网行动为什么给的钱那么多
因为护网行动是国家应对网络安全问题所做的重要布局之一。 随着大数据、物联网、云计算的快速发展,愈演愈烈的网络攻击已经成为国家安全的新挑战。国家关键信息基础设施可能时刻受到来自网络攻击的威胁。网络安全的态势之严峻,迫切需要我们在网络安全领…...

软考知识汇总-计算机系统
文章目录 1 计算器 1 计算器 算术逻辑单元(ALU):运算器重要组成部件,负责处理数据,实现对数据的算数运算和逻辑运算。累加寄存器(AC):简称累加器,为ALU提供数据并暂存运…...

OpenCV 11(图像金字塔)
一、 图像金字塔 **图像金字塔**是图像中多尺度表达的一种,最主要用于图像的分割,是一种以多分辨率来解释图像的有效但概念简单的结构。简单来说, 图像金字塔是同一图像不同分辨率的子图集合. 图像金字塔最初用于机器视觉和图像压缩。其通过梯次向下采…...

Linux学习笔记-Ubuntu系统用户、群组、权限管理
一、概述 本文记录Ubuntu系统下通过命令操作用户账户进行管理。 Ubuntu系统版本: Linux ubuntu 5.15.0-1034-raspi #37-Ubuntu SMP PREEMPT Mon Jul 17 10:02:14 UTC 2023 aarch64 aarch64 aarch64 GNU/Linux 注:查看系统版本号的指令如下 uname -…...

文章预览 安防监控/视频存储/视频汇聚平台EasyCVR播放优化小tips
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。为了便于用户二次开发、调用与集成,…...
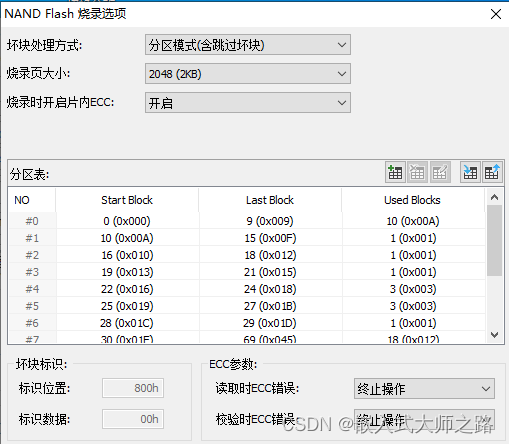
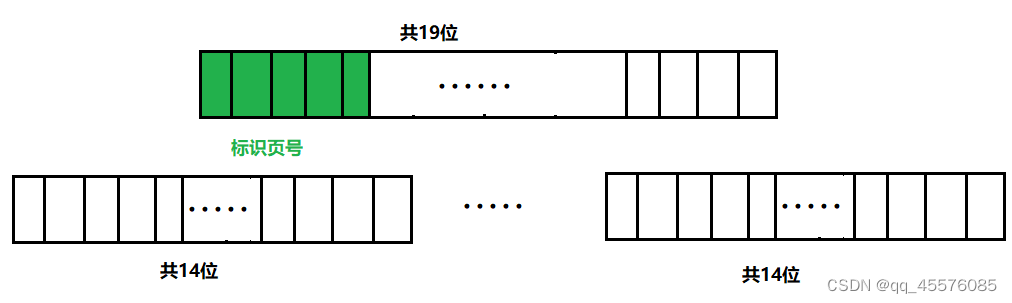
Nand Flash的特性及烧录问题
目录 前言 一 Nand flash的特性 1 存储结构 2 OOB区域 3 位翻转 4 坏块及ECC 二 Nand系统裸片量产烧录 1 坏块处理策略 2 分区(Partition) 3 纠错码(Error Correction Codes,ECC) 4. 擦除坏块 🎈个人主页🎈:linux_嵌入式…...

【React 】useLayoutEffect 和 useEffect的区别
useLayoutEffect和useEffect是React中常用的两个Hook,它们的主要区别在于触发时机。 useEffect会在渲染完成后异步执行,不会阻塞浏览器的绘制操作。它适用于需要在组件渲染后执行副作用的情况,例如数据的获取、订阅事件等。它不会阻止屏幕更新…...

oracle数据库常见的优化步骤与脚本
要优化 Oracle 数据库的性能,可以按照以下步骤进行: 1. 性能分析和诊断:首先,使用 Oracle 提供的性能分析工具(如 AWR 报告、ASH 报告)对数据库进行分析和诊断。这些报告可以帮助您确定数据库的性能瓶颈和潜在问题。 2. 优化 SQL 查询语句:针对频繁执行的 SQL 查询语句…...
并发内存池(C++)
项目简介 这个项目是实现了一个高效的并发内存池。它的原型的goggle的一个开源项目tcmalloc,即thread-cache malloc(线程缓存的malloc),实现了高效多线程的内存管理,可实现对系统提供的内存分配函数malloc和free的替代…...

本地起一个VUE 前端项目
#安装 安装 Vue CLI 3: Vue CLI是一个用于创建和管理Vue项目的命令行工具 npm install -g vue/cli#查看更详细的告警信息 npm install -g vue/cli --verbose#检查项目的依赖关系 ,保持项目的依赖关系最新和安全 npm audit npm audit fix#查看版本 vue --version#创建…...

Python爬虫:Selenium的介绍及简单示例
Selenium是一个用于自动化Web应用程序测试的开源工具。它允许开发人员模拟用户在浏览器中的交互行为,以便自动执行各种测试任务,包括功能测试、性能测试和回归测试等。Selenium最初是为Web应用程序测试而创建的,但它也可用于Web数据抓取和其他…...

每日刷题|回溯法解决全排列问题第二弹之解决字符串、字母大小排列问题
食用指南:本文为作者刷题中认为有必要记录的题目 前置知识:回溯法经典问题之全排列 ♈️今日夜电波:带我去找夜生活—告五人 0:49 ━━━━━━️💟──────── 4:59 …...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...
