[学习笔记]CS224W
资料:
课程网址
斯坦福CS224W图机器学习、图神经网络、知识图谱【同济子豪兄】
斯坦福大学CS224W图机器学习公开课-同济子豪兄中文精讲
图的基本表示
图是描述各种关联现象的通用语言。与传统数据分析中的样本服从独立同分布假设不一样,图数据自带关联结构,数据和数据,样本和样本之间有联系。
图神经网络是端到端的表示学习,无需人工特征工程,可以自动学习特征(类似CNN)。
图神经网络的目标是实现图嵌入,即将一个节点映射成d维向量,同时保证网络中相似的节点有相近的向量表示。这个d维向量应该包含节点在原图中的结构信息,语意信息,以方便后续的数据挖掘。
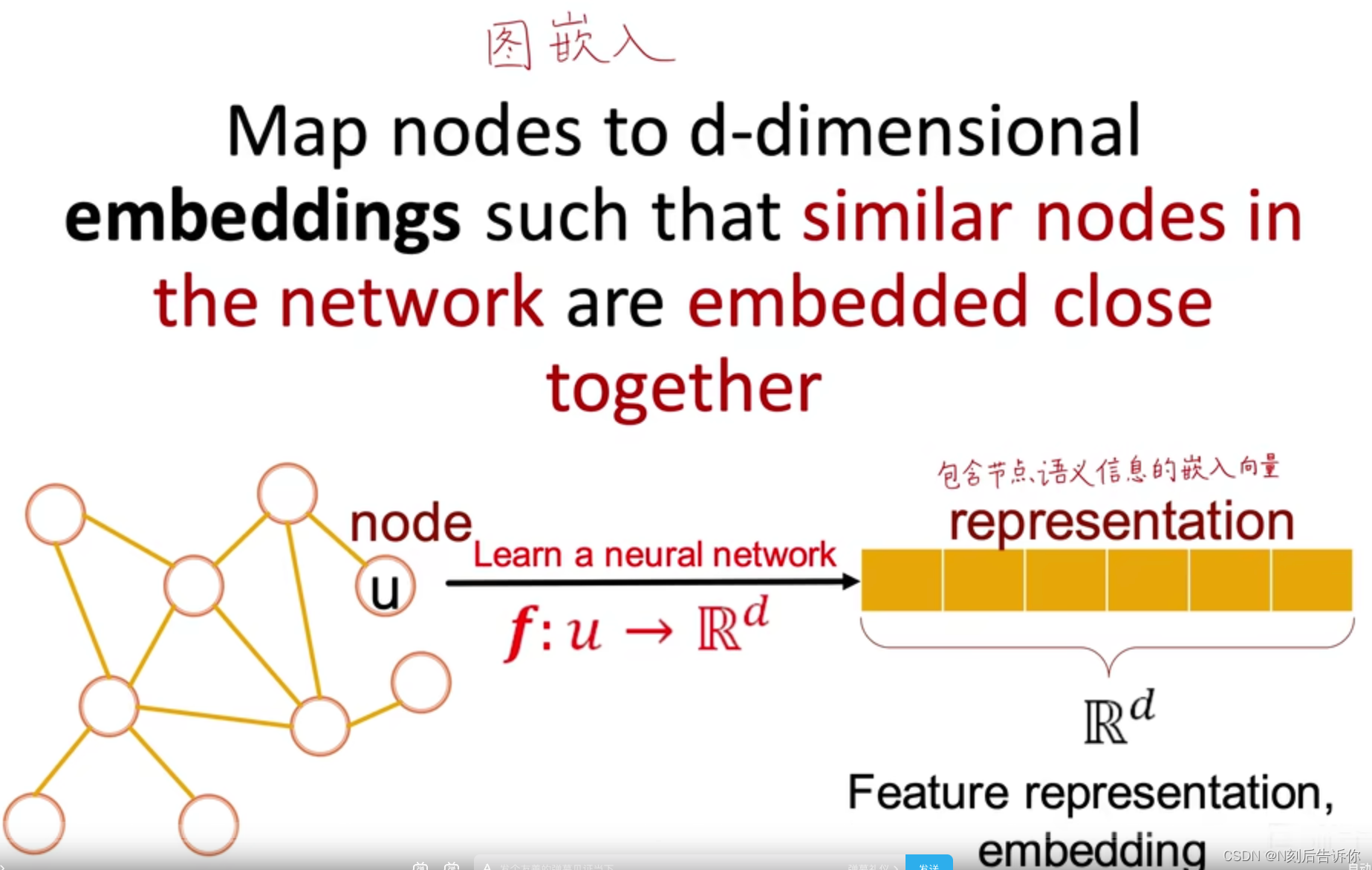
节点、连接、子图、全图都可以带有特征
不同的任务
在节点、连接、子图、全图层面,都可以进行图数据挖掘
- 节点层面的案例:如信用卡欺诈
- 连接层面的案例:如推荐可能认识的人
- 子图层面的案例:如用户聚类
- 全图层面的案例:全图层面的预测,如分子是否有毒;全图层面的生成,如生成新的分子结构
图的本体设计
图(network/graph)由节点(nodes/vertices)和连接(links/edges)组成。
节点的集合用
N表示,连接的集合用E表示,整个图用G(N,E)表示。
本体图
图的设计牵涉到一个概念,本体图(Ontology)。本体图应该显示节点可能的类型,以及各类型节点(包括节点类型到其自身)之间可能存在的关系。如下图,是一个医疗领域的知识图谱的本体图。
如何设计本体图,取决于要解决的问题。如下图,例如要解决的问题是,什么疾病可以吃什么,那么疾病和食物就需要设计成节点。可以吃,不可以吃, 不推荐吃就应该设计成节点之间的关系
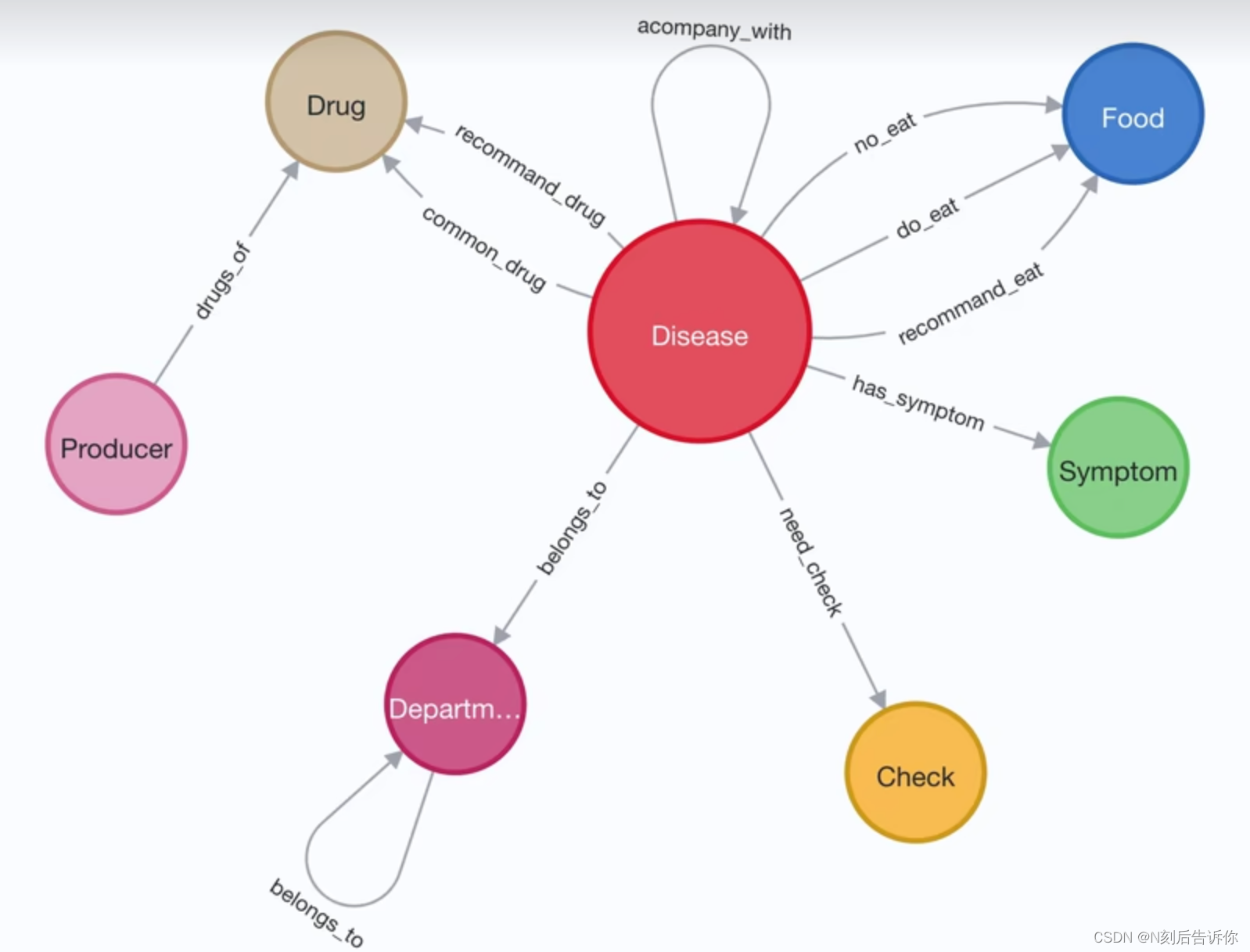
有时本体图是唯一、无歧义的,如社交网络
有时本体图不唯一,取决于你要研究的问题,如考虑红楼梦的家族,地点,事件等
图的种类(有向、无向、异质、二分、连接带权重)
图可以分为无向图、有向图、异质图(heterogeneous graph)、二分图。
- 无向图:对称的、双向的图。如合作关系,facebook上的好友关系
- 有向图:单向的图。如电话,Twitter上的关注
- 异质图:节点和连接可能有不同的类型,是很多论文研究的重点
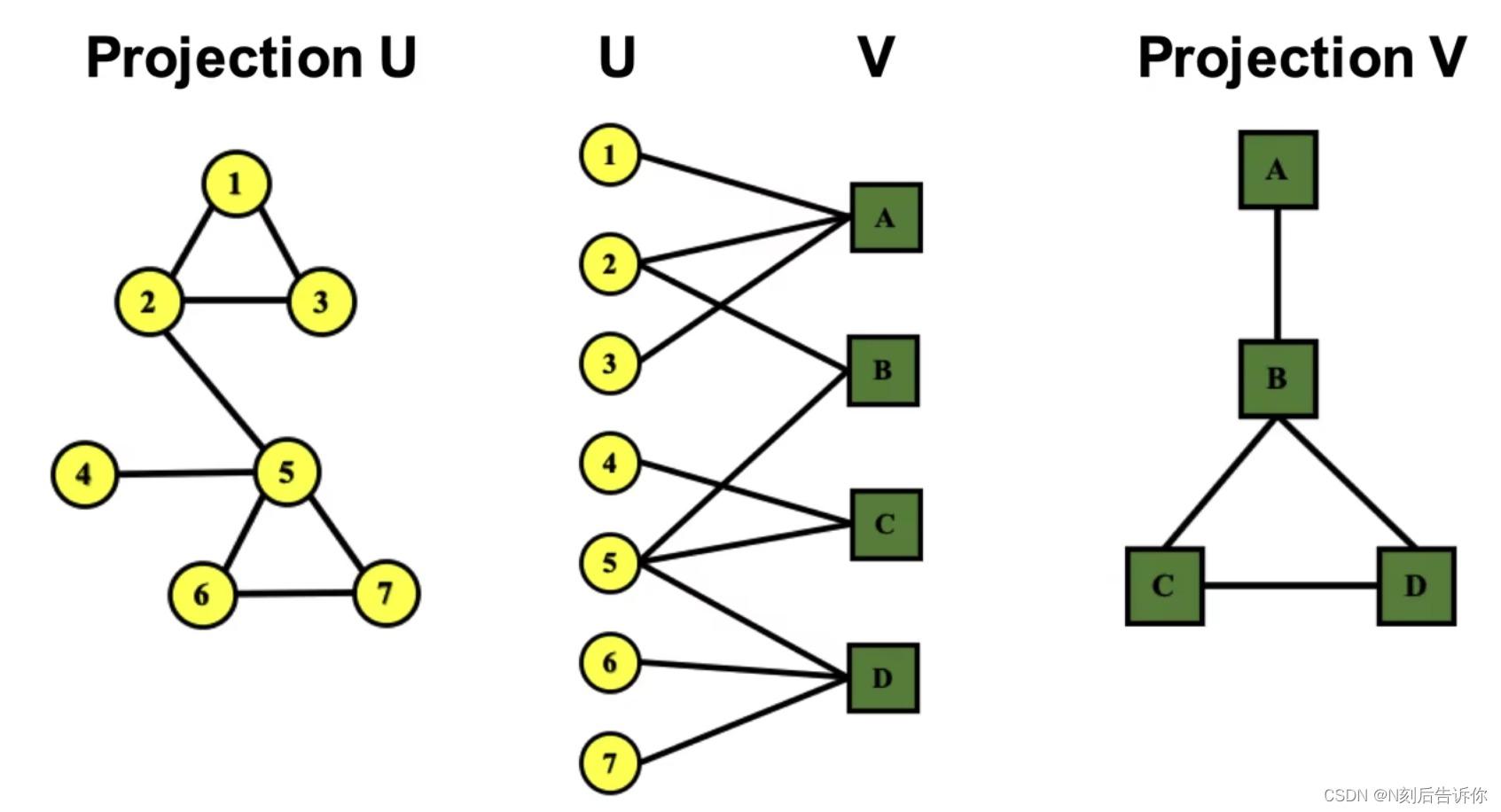
- 二分图(Bipartite Graph):节点种类是2的异质图被称为二分图。如论文作者和论文的关系、用户和商品之间的关系
二分图可以展开,如下图,在节点集U中,如果两个节点都连接到V中的同一个节点,则在图
Projection U中添加一条连接。
这样就可以将二分图转化为两张各自只有一类节点的图。
节点的度(Node degree)
-
对于无向图
-
- 第
i个节点的度:记为 k i k_i ki,表示与第i个节点邻接的边的数量
- 第
-
- 图的平均度: k ˉ = ⟨ k ⟩ = 1 N ∑ i = 1 N k i = 2 E N \bar{k}=\langle k\rangle=\frac{1}{N} \sum_{i=1}^N k_i=\frac{2 E}{N} kˉ=⟨k⟩=N1∑i=1Nki=N2E
-
对于有向图
-
- 入度:从别的节点指向当前节点的边的总数
-
- 出度:从当前节点指向别的节点的边的总数
-
- 节点的度=入度+出度
-
- 图的平均度: k ˉ = E N \bar{k}=\frac{E}{N} kˉ=NE
平均入度=平均出度,因为一个出度对应的边必然对应一个入度对应的边
入度为0的节点称为Source,出度为0的节点称为Sink
- 图的平均度: k ˉ = E N \bar{k}=\frac{E}{N} kˉ=NE
节点的度可以一定程度上反应节点的重要程度
图的基本表示-邻接矩阵
- 无向图
如果第i个节点和第j个节点之间存在边,则邻接矩阵A的 A i j A_{ij} Aij和 A j i A_{ji} Aji对应的值为1
无向图对应的邻接矩阵是对称阵
如果没有自身到自身的环,则主对角线全为0
- 有向图
如果第i个节点存在指向第j个节点之间的边,则邻接矩阵A的 A i j A_{ij} Aij对应的值为1
有向图对应的邻接矩阵是非对称阵
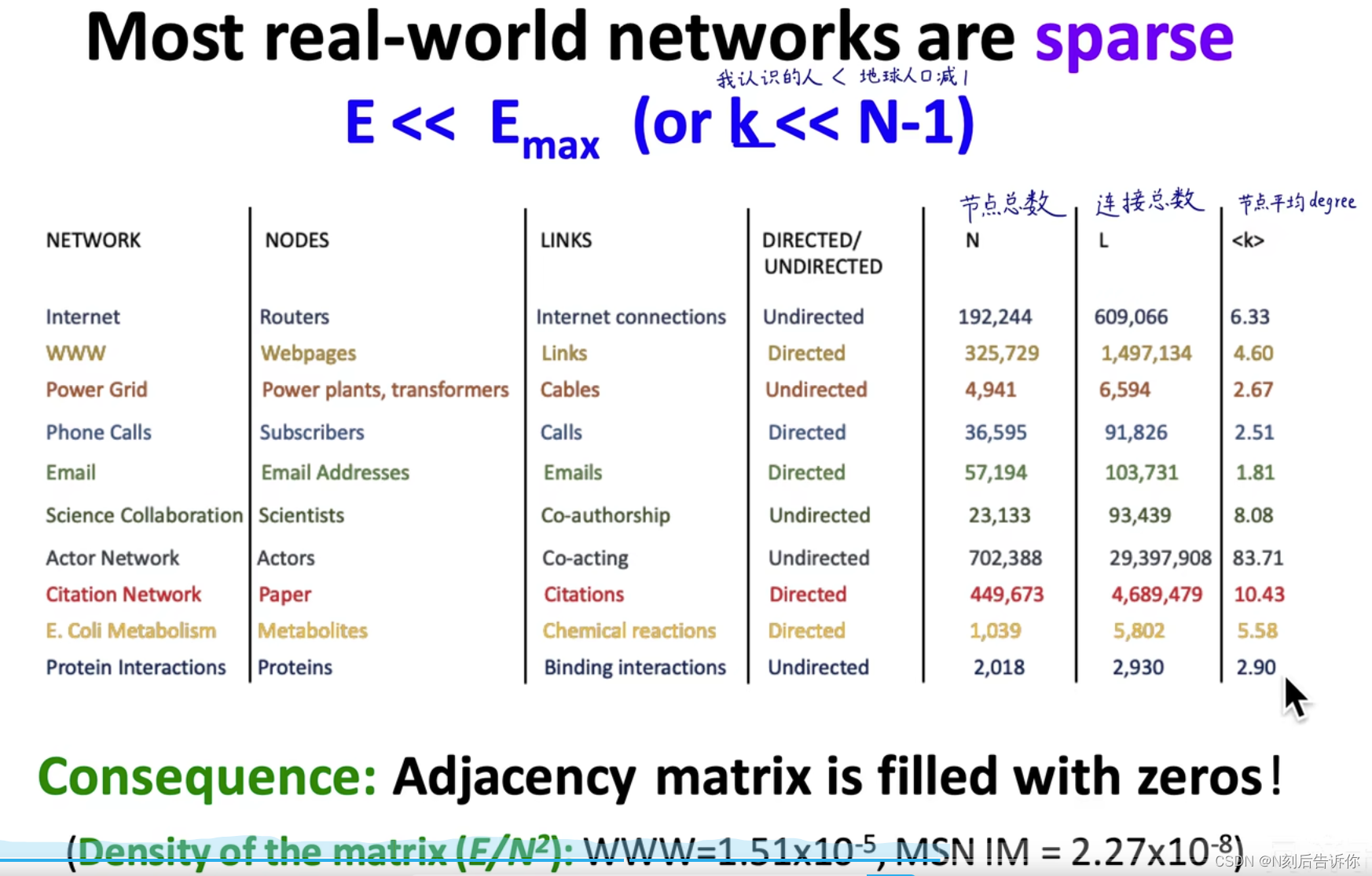
邻接矩阵是稀疏的,如社交网络
图的基本表示-连接列表和邻接列表
如上面所示,用邻接矩阵来表示图,存在稀疏性问题,造成存储空间的浪费。
- 连接列表:只记录存在连接的边和节点

- 邻接列表:对于一个给定节点,只记录他指向的节点和对应的边

上述图是无权图,在邻接矩阵中的值非1即0,如果是带权图,则可以在邻接矩阵中将1改成权重。
图的连通性
-
无向图中
连通图(Connected graph):任意两个点都有一条路径可达,则称为连通图。
不连通图虽然本身不连通,但是可以划分得到多个连通分支(connected components)。最大的连通分支被称为Giant Component
孤立的节点称为Isolated node。
不连通矩阵的邻接矩阵呈现出分块对角的形式
如果存在一个节点将不连通图的两个连通分支连接上了,那么它会打破分块对角形式 -
有向图中
强连通的有向图:如果任意两个节点存在有向路径可达,则称为强连通的有向图。
弱连通的有向图:如果忽略边的方向,即将它看成无向图,此时如果图是连通的,那么这个有向图称为弱连通的。对于有向图,可能整体不是强连通的,但其中的某个子图是强连通的,称为强连通分支(Strongly connected components(SCC))
E和G指向SCC,称为In-componet、D和F是由SCC出发的,称为Out-component。
传统图机器学习的特征工程-节点
-
总的思路
本节用传统机器学习方法,做特征工程,人工设计一些特征,把节点,边,全图特征编码成d维向量,再用该向量进行后续机器学习预测。 -
1.特征工程
抽取d个特征,编码为d维向量。本节只考虑连接特征,不考虑属性特征。节点自己的特征,称为属性特征(Attributes)
节点和图中其他节点的连接关系,称为连接特征。 -
2.训练一个机器学习模型
利用RF、SVM、NN等进行训练。 -
3.应用模型
给定一个新的节点/链接/图,获得图她的特征并做预测。
本节主要聚焦无向图,并针对节点、边、图层面做特征工程。
节点层面的特征工程
目标:区分节点在图中的结构和位置,可考虑的(连接)特征有:节点的度(Node degree)、节点的重要度(Node centrality)、聚类系数(Clustering coefficient)、子图模式(Graphlets)
聚合系数是指,与当前节点邻接的节点是否有联系。
Node degree
Node degree只考虑了邻接节点的数量,不能反应节点的质量
Node centrality
Node centrality考虑了节点在图中的重要度。有不同的方式来对此进行建模:
-
特征向量重要度(Eigenvector centrality)
思想:如果一个节点的邻接节点很重要,那么这个节点也很重要
建模:
c v = 1 λ ∑ u ∈ N ( v ) c u c_v=\frac{1}{\lambda}\sum_{u \in N(v)} c_u cv=λ1u∈N(v)∑cuλ \lambda λ是归一化系数,往往是A的最大特征值
实现:这是一个递归问题,如何解决?
上面公式等价于求解 λ c = A c \lambda \boldsymbol{c}=\boldsymbol{A c} λc=Ac可以发现, c \boldsymbol{c} c向量就是 A \boldsymbol{A} A的最大特征值对应的特征向量
根据perron-frobenius定理,最大特征值 λ m a x \lambda_{max} λmax一定为正且唯一 -
Betweenness centrality
思想:如果在任意两个节点间的最短路径中,有一个节点频繁出现,那么这个节点可以被认为是重要的
建模:
c v = ∑ s ≠ v ≠ t # ( shortest paths betwen s and t that contain v ) # ( shortest paths between s and t ) c_v=\sum_{s \neq v \neq t} \frac{\#(\text { shortest paths betwen } s \text { and } t \text { that contain } v)}{\#(\text { shortest paths between } s \text { and } t)} cv=s=v=t∑#( shortest paths between s and t)#( shortest paths betwen s and t that contain v)

-
Closeness centrality
思想:如果一个节点到其他所有节点的路径都很短,那么这个节点可以被认为是重要的
建模:
c v = 1 ∑ u ≠ v shortest path length between u and v c_v=\frac{1}{\sum_{u \neq v} \text { shortest path length between } u \text { and } v} cv=∑u=v shortest path length between u and v1
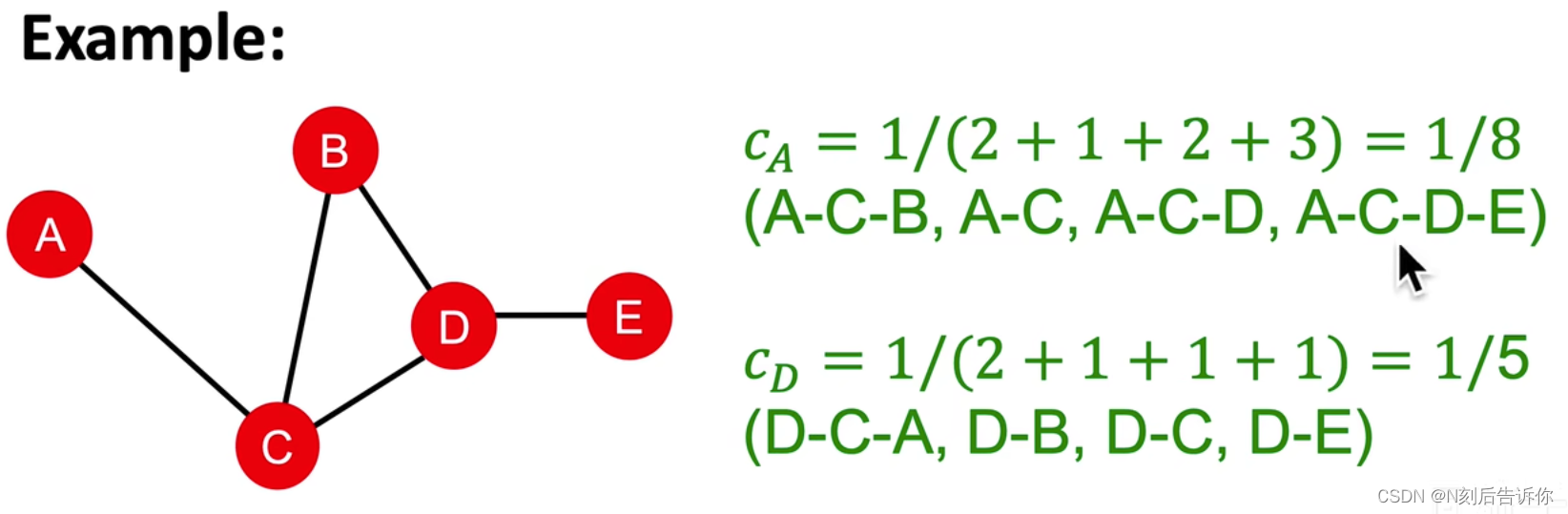
Clustering Coefficient
聚类系数(Clustering Coefficient),衡量一个节点的邻接节点的连接有多紧密。
建模:
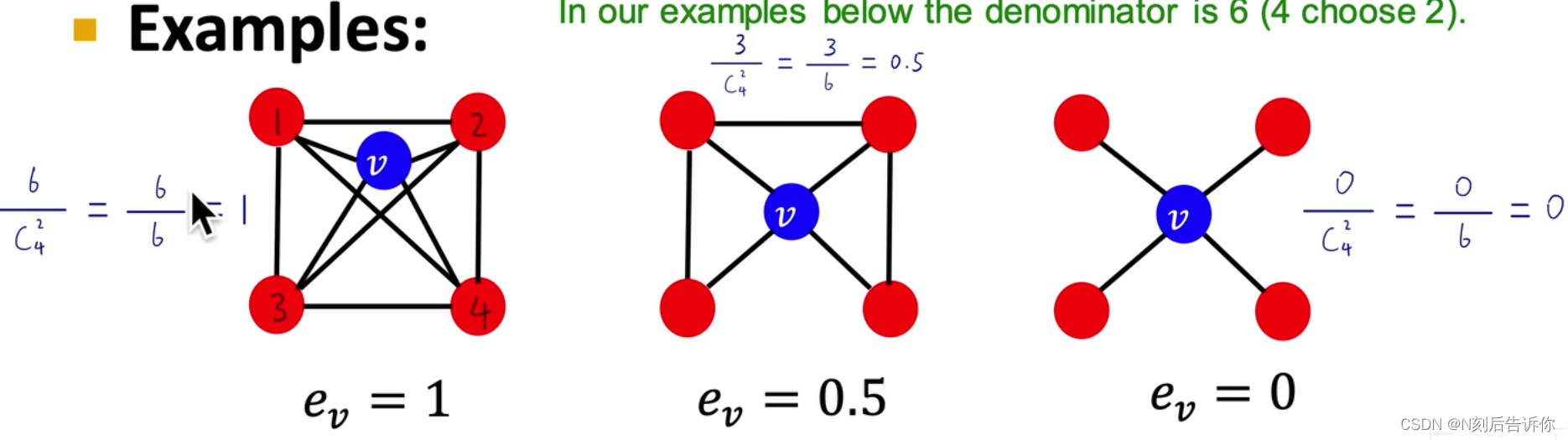
e v = # ( edges among neighboring nodes ) ( k v 2 ) ∈ [ 0 , 1 ] e_v=\frac{\#(\text{edges among neighboring nodes})}{\binom{k_v}{2}}\in [0, 1] ev=(2kv)#(edges among neighboring nodes)∈[0,1]
v节点相邻节点两两组成的节点对计入分母
如果节点对中的两个节点相邻,那么这对节点对计入分子
Graphlets
一个节点的自我网络(ego-network)是指以一个节点为中心,只包含他和他邻接节点,以及这些节点之间的边的图。
可以发现,节点v的聚类系数本质上就是计数了节点v的自我网络中以v为顶点的三角形的个数。
这个三角形可以理解为我们预先定义的一类子图。
那么如果修改这个预定义的子图类型,就可以得到新的计数特征,这个预定义的子图类型,就是我们下面要提到的graphlets。
先看看子图、生成子图、导出子图的概念:
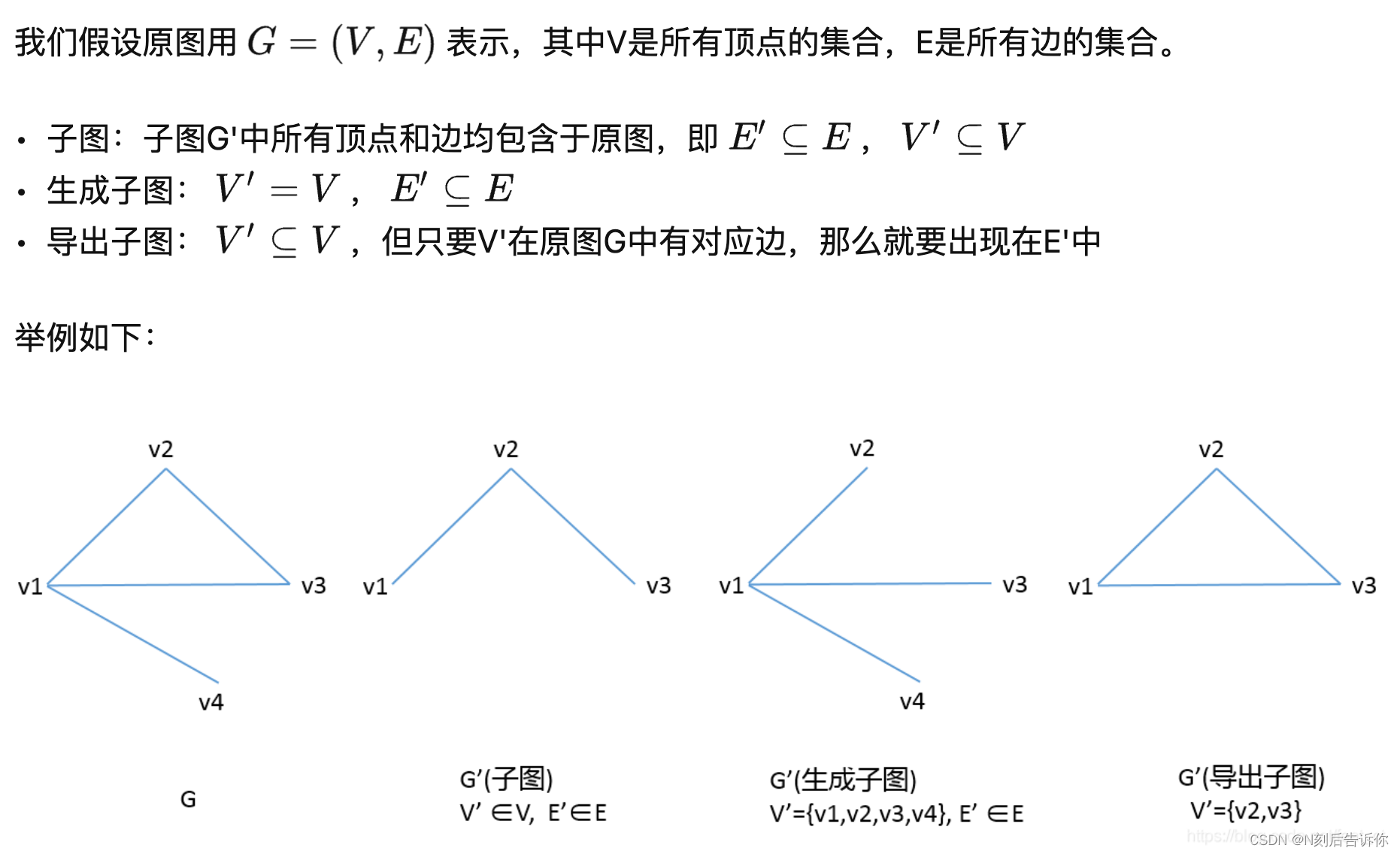
可以看到,从原图中取一些节点,并取这些节点所有出现的边可以构成导出子图。
下面给出Graphlets的精确定义,即有根连通导出异构子图(Rooted connected induced non-isomorphic subgraphs)
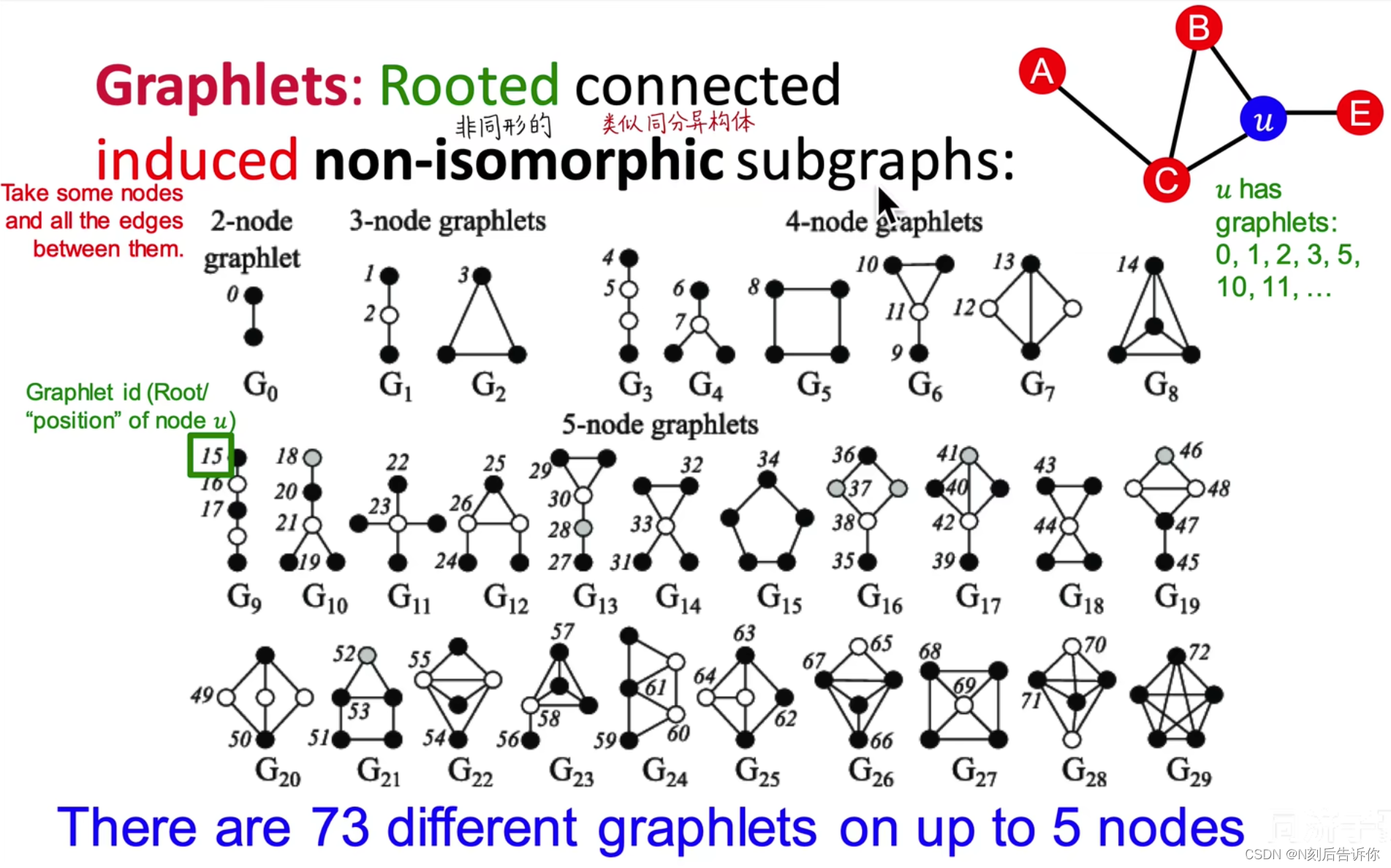
上图分别展示了2节点、3节点、4节点和5节点的graphlets,共有73种。
2个节点构成的子图中,可以定义1种类型的graphlet
3个节点构成的子图中,可以定义3种类型的graphlets
…
在右上角的例子中,节点u对应的graphlets类型有0、1、2、3、5、10、11、…
聚类系数中的三角形其实就是G2对应的graphlet。
下面引入Graphlets相关的特征向量:Graphlets Degree Vector(GDV),它一个基于给定节点,以它为根的各类graphlets的实例个数组成向量,如下面的例子。
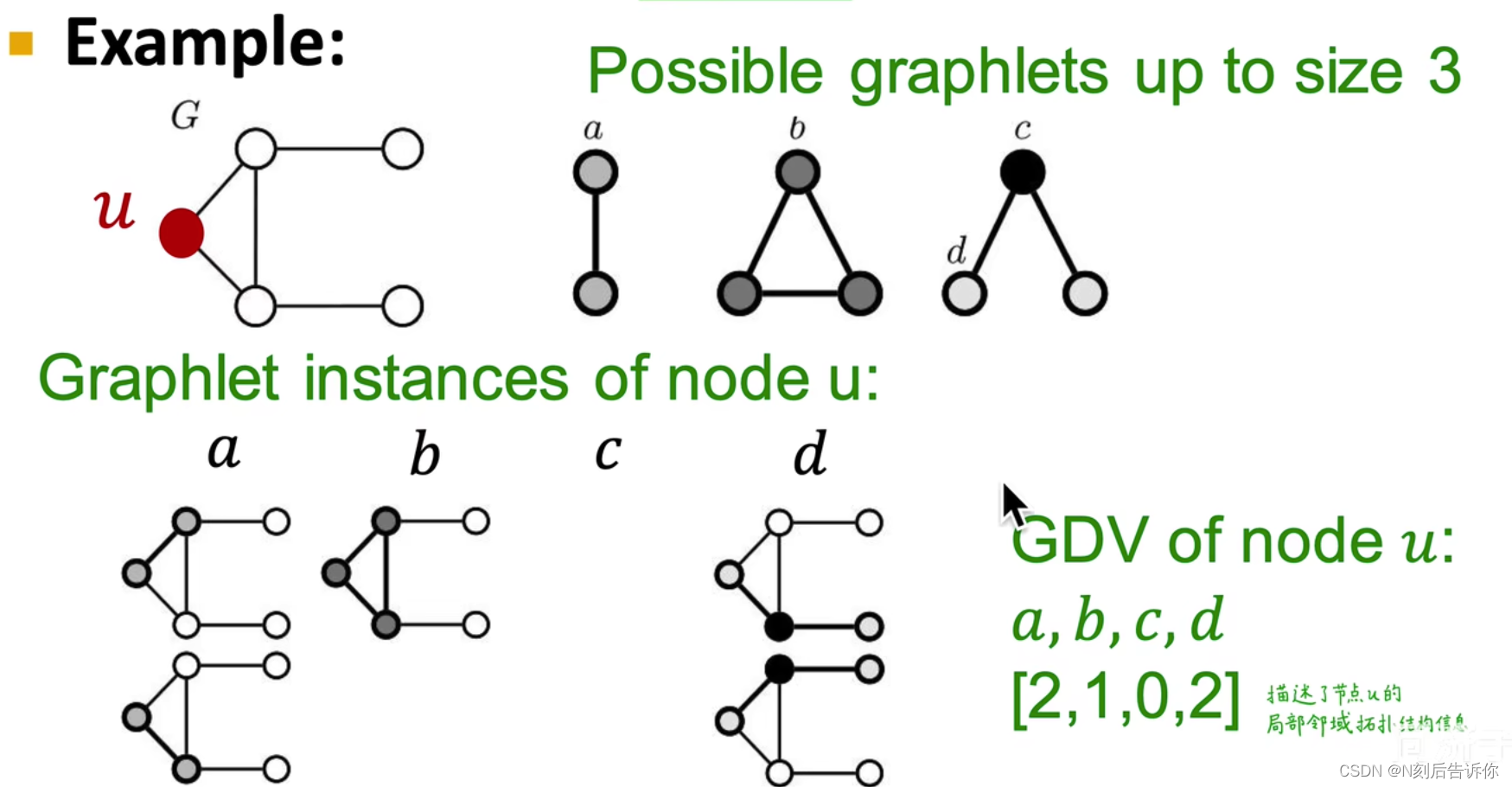
注意,原图中没有以c为根结点的导出子图。
GDV描述了节点局部领域的拓扑结构信息,用一些已经定义好的子图模式去匹配,并计数每种模式下的数量。
比较两个节点的GDV向量,可以计算距离和相似度。
在NetworkX中,子图模式Graphlets被称为Atlas
总结
介绍的结构特征可以分为:
基于重要度的特征(描述节点中心度/重要度):
- 节点的度
- 不同节点的重要度度量
可用于预测有影响力的节点
基于结构的特征(描述节点的邻域拓扑连接结构):
- 节点的度
- 聚类系数
- GDV
可用于预测节点在图中的功能,桥接、枢纽、中心
传统图机器学习的特征工程-连接
连接层面的预测任务:基于已知连接去预测(补全)未知连接。
在模型训练阶段,节点对被排序,top K节点对被预测。
关键是如何设计节点对的特征。
思路1:直接提取link的特征,变成d维向量。
思路2:把link两端的d维向量拼在一起,但是这会丢失link本身连接结构信息。
link prediction task有两种情况:
-
随机丢失连接:
对于客观静态图,如蛋白质,分子,我们可以通过随机移除一些连接,并尝试预测它们 -
随时间变化的连接:
对于如论文引用、社交网络、微信好友、学术合作等图,给定一段时间 [ t 0 , t 0 ′ ] [t_0, t_0^{'}] [t0,t0′]的图,预测下一个时间段 [ t 1 , t 1 ′ ] [t_1, t_1^{'}] [t1,t1′]的一个关于边的ranked list L。
评估的方式:先计算得到 [ t 1 , t 1 ′ ] [t_1, t_1^{'}] [t1,t1′]内真实出现的边的数量,记为 n = ∣ E n e w ∣ n=|E_{new}| n=∣Enew∣,然后从上面预测的列表中选出top n条边,然后计算预测的n个连接的准确率。
准确率 = 预测的 t o p n 个连接中正确的数量 n 准确率 = \frac{预测的top\ n个连接中正确的数量}{n} 准确率=n预测的top n个连接中正确的数量
连接层面的特征
连接的特征可以分为三类:基于距离的特征、基于两节点局部邻域信息的特征、基于两节点全局领域信息的特征
两节点的最短路径长度
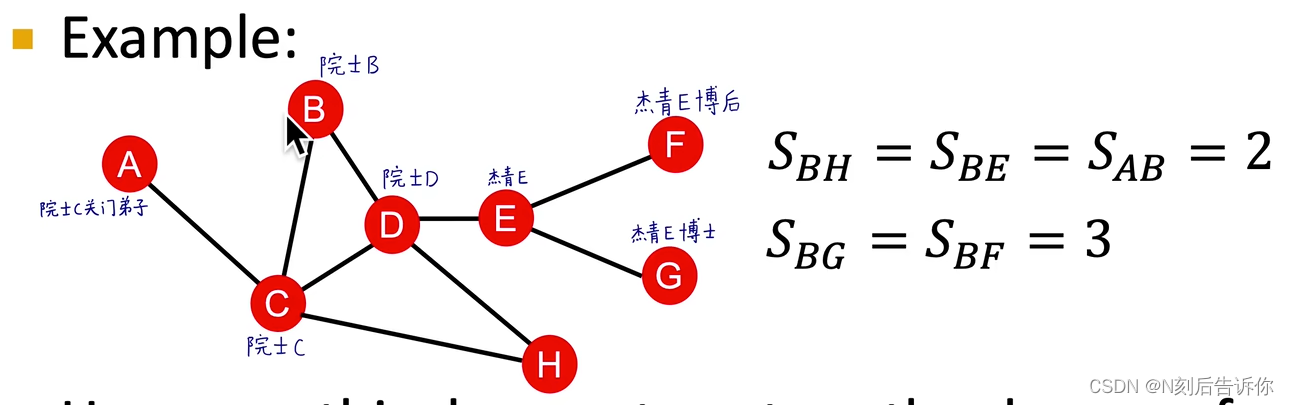
但仅考虑最短路径长度,会忽略连接的质量。如同样最短路径长度是2,A和B只有一条通路,而B和H有两条。
基于两节点局部邻域的信息
考虑两个节点v1和v2的邻接节点。
-
Common neighbors:
思路:记录共同好友个数
公式:
∣ N ( v 1 ) ∩ N ( v 2 ) ∣ \left|N\left(v_1\right) \cap N\left(v_2\right)\right| ∣N(v1)∩N(v2)∣ -
Jaccard’s coefficient:
思路:共同好友个数/两节点邻接节点的并集
公式:
∣ N ( v 1 ) ∩ N ( v 2 ) ∣ ∣ N ( v 1 ) ∪ N ( v 2 ) ∣ \frac{\left|N\left(v_1\right) \cap N\left(v_2\right)\right|}{\left|N\left(v_1\right) \cup N\left(v_2\right)\right|} ∣N(v1)∪N(v2)∣∣N(v1)∩N(v2)∣ -
Adamic-Adar index:
思路:共同好友是不是社牛,如果v1和v2的共同好友是社牛,那么v1和v2的联系就很廉价。
公式:
∑ u ∈ N ( v 1 ) ∩ N ( v 2 ) 1 log ( k u ) \sum_{u \in N\left(v_1\right) \cap N\left(v_2\right)} \frac{1}{\log \left(k_u\right)} u∈N(v1)∩N(v2)∑log(ku)1
基于两节点的局部邻域信息的特征的缺点是:对于没有共同好友的两节点,他们的上述度量都是0。
但事实上,他们在未来可能会有连接。
而全局领域的信息度量可以解决这个缺陷。
基于两节点全局领域的信息
Katz index:
思路:计数节点u和v之间所有长度路径的加权和
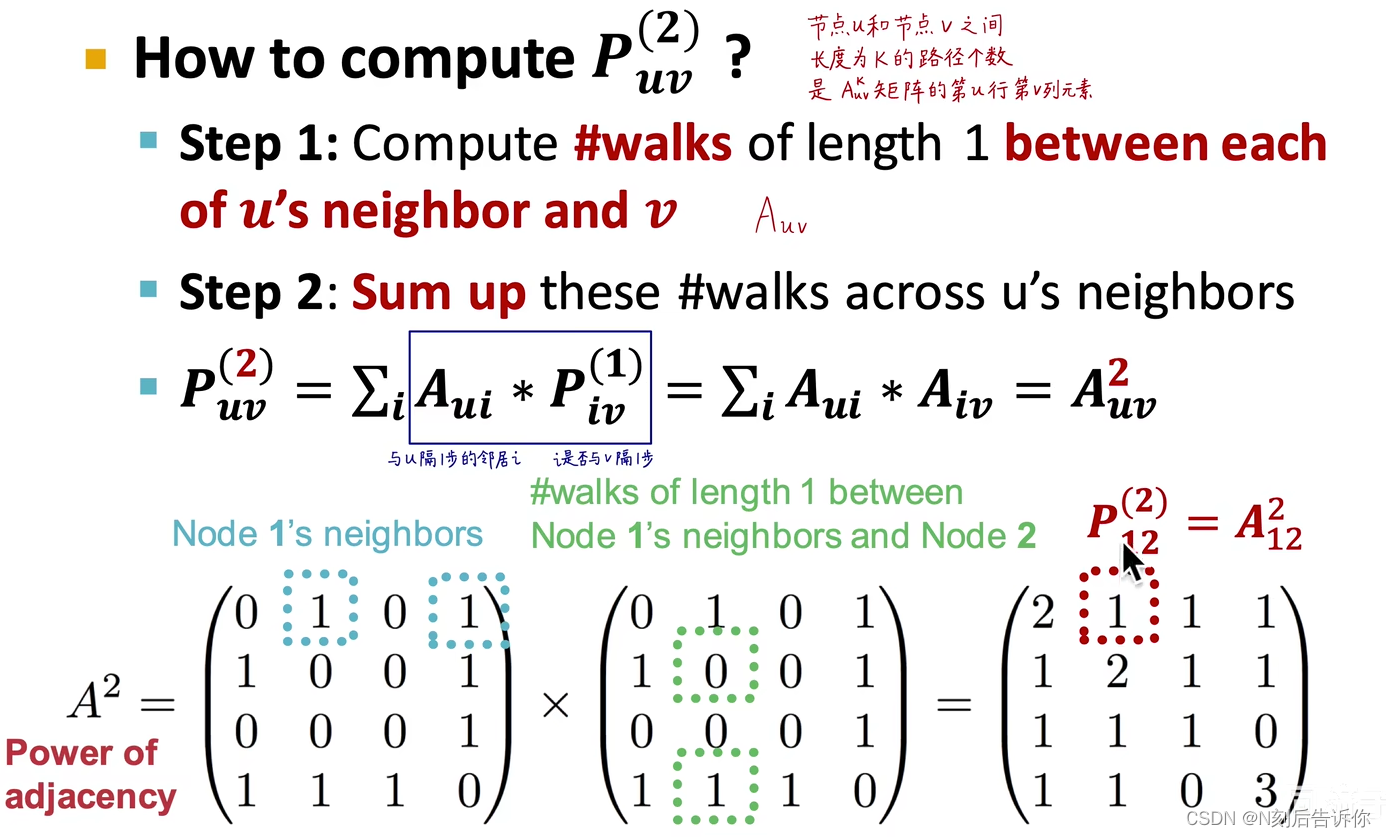
可以使用图邻接矩阵的幂可以结算长度为k的路径个数
结合下图,利用数学归纳法,可以推导出 A u v l A_{u v}^l Auvl表示节点u和v之间长度为l的路径个数。
公式:
S v 1 v 2 = ∑ l = 1 ∞ β l A v 1 v 2 l S_{v_1 v_2}=\sum_{l=1}^{\infty} \beta^{l} A_{v_1 v_2}^l Sv1v2=l=1∑∞βlAv1v2l
其中, 0 < β < 1 0<\beta<1 0<β<1表示折减系数
它的等价矩阵形式是(类比等比数列求和,并求无穷级数可得):
( I − β A ) − 1 − I (\boldsymbol{I}-\beta \boldsymbol{A})^{-1}-\boldsymbol{I} (I−βA)−1−I
一般可以将最大特征值的倒数作为折减系数 β \beta β
传统图机器学习的特征工程-全图
目标:将全图 G G G的结构特点表示为一个d维特征向量 ϕ ( G ) \phi(G) ϕ(G)。
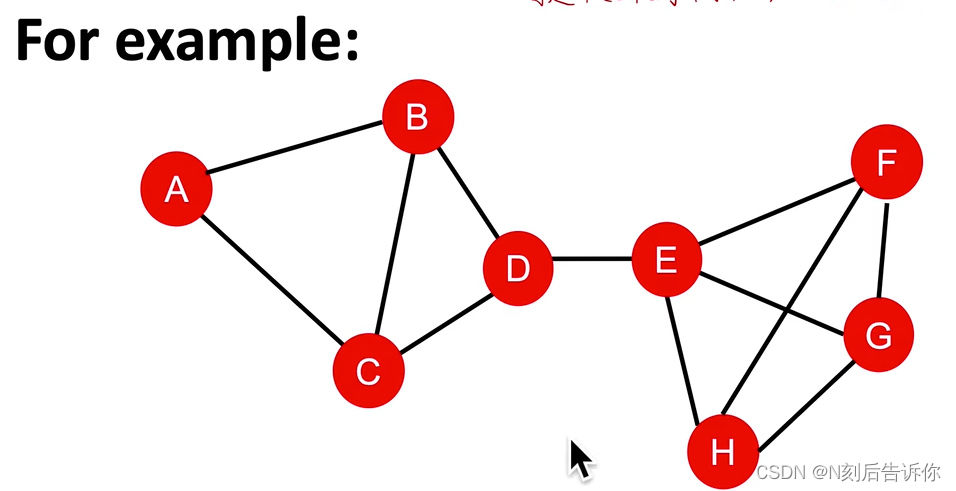
Bag-of-*
思路:类比NLP中的Bag-of-Words,
Bag-of-nodes.
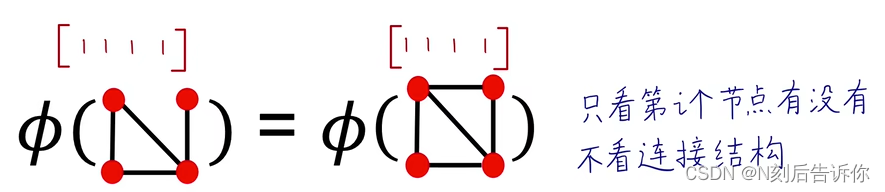
Bag-of-node degrees
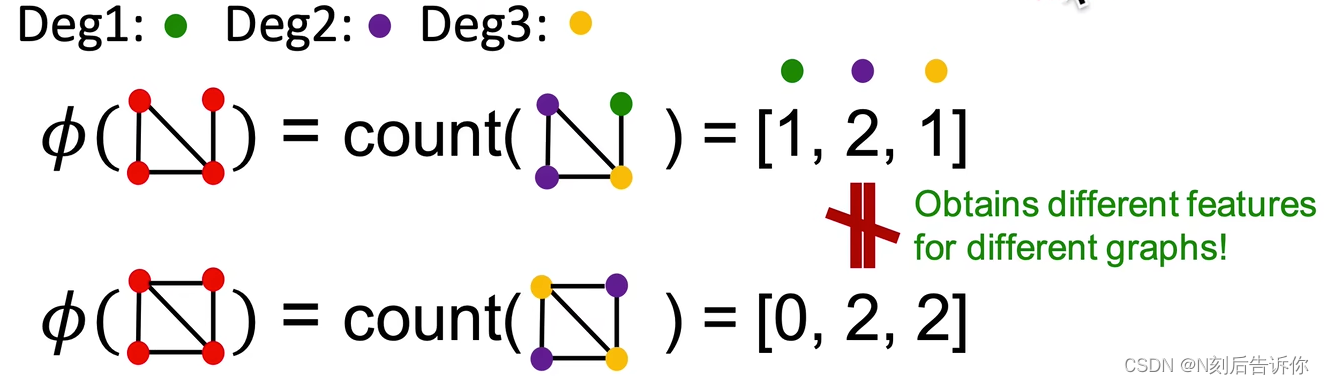
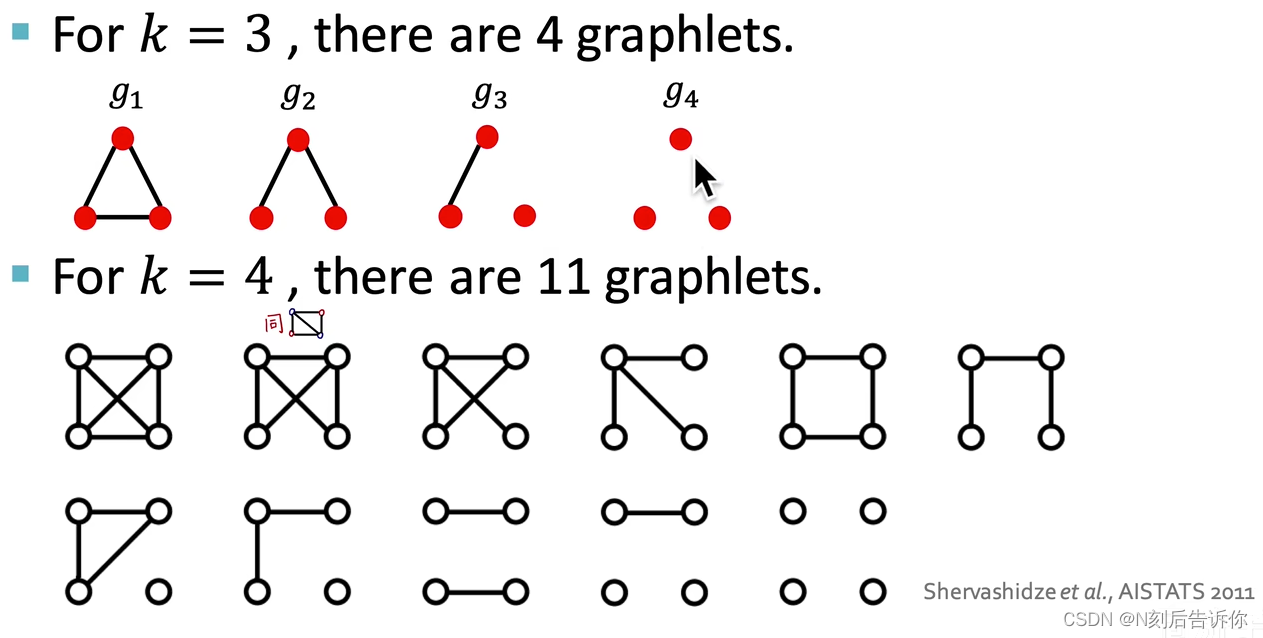
Bag-of-graphlets
注意,这里是从全图的视角去分析,所以这里的graphlets和前面在节点特征工程中提到的graphlets有两点不同:
可以存在孤立节点的graphlets
graphlets不区分根,如下图,g2对应一个graphlets,而不是两个(如果考虑根,是两个)
Graphlet Count Vector:给定一个图G,和graphlets列表 G k = ( g 1 , g 2 , . . . g n k ) G_k=(g_1,g_2, ... g_{n_k}) Gk=(g1,g2,...gnk),Graphlet Count Vector可以定义为(向量的第i个分量可以定义为第i个graphlet在全图中的个数):
( f G ) i = # ( g i ⊆ G ) for i = 1 , 2 , … , n k \left(f_G\right)_i=\#\left(g_i \subseteq G\right) \text { for } i=1,2, \ldots, n_k (fG)i=#(gi⊆G) for i=1,2,…,nk
例子:
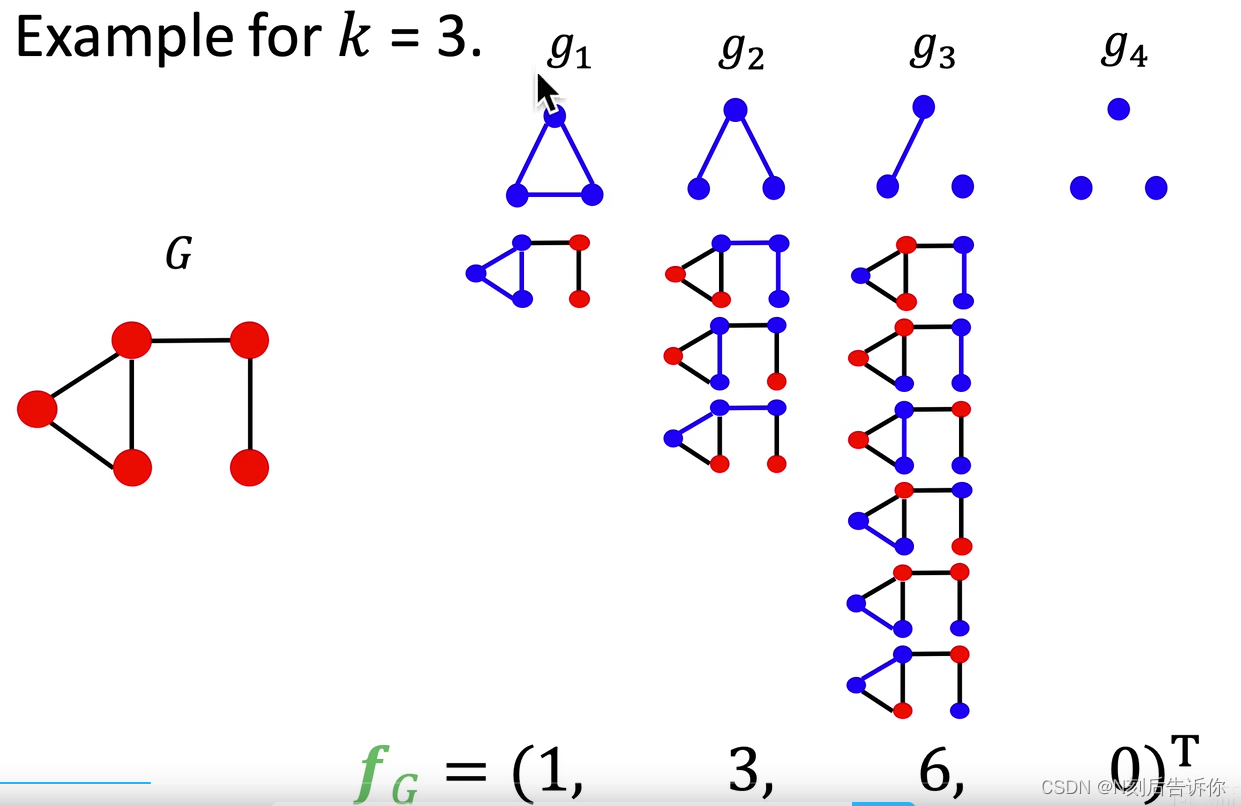
给定两个图, G G G和 G ′ G' G′,且有了它们对应的GCV,进一步,可以计算Graphlet Kernel:
K ( G , G ′ ) = f G T f G ′ K\left(G, G^{\prime}\right)=\boldsymbol{f}_G^{\mathrm{T}} \boldsymbol{f}_{G^{\prime}} K(G,G′)=fGTfG′
它可以反应这两张图的关系。
如果两个GCV的数量级悬殊,那么则需要先对这两个特征向量作归一化: h G = f G Sum ( f G ) \boldsymbol{h}_G=\frac{\boldsymbol{f}_G}{\operatorname{Sum}\left(\boldsymbol{f}_G\right)} hG=Sum(fG)fG,再计算Graphlet Kernel: K ( G , G ′ ) = h G T h G ′ K\left(G, G^{\prime}\right)=\boldsymbol{h}_G{ }^{\mathrm{T}} \boldsymbol{h}_{G^{\prime}} K(G,G′)=hGThG′
获取GCV在算力上是很昂贵的,在大小为n的图上对大小为k的graphlet作子图匹配,需要的时间复杂度是多项式复杂度: O ( n k ) O(n^k) O(nk)。
即使图节点的度被限制为 d d d,复杂度也仍有 O ( n d k − 1 ) O(nd^{k-1}) O(ndk−1)
Weisfeiler-Lehman Kernel
由于Graphlets Kernel不够高效,下面引入更高效的Weisfeiler-Lehman Kernel。
目标:设计一个更高效的特征编码。
思路:使用邻域结构迭代式地丰富节点词库
算法实现:颜色微调
主要的步骤是:
- 1.初始化颜色
- 2.聚合邻域的颜色+对聚合后的颜色进行哈希映射:
c ( k + 1 ) ( v ) = HASH ( { c ( k ) ( v ) , { c ( k ) ( u ) } u ∈ N ( v ) } ) c^{(k+1)}(v)=\operatorname{HASH}\left(\left\{c^{(k)}(v),\left\{c^{(k)}(u)\right\}_{u \in N(v)}\right\}\right) c(k+1)(v)=HASH({c(k)(v),{c(k)(u)}u∈N(v)})
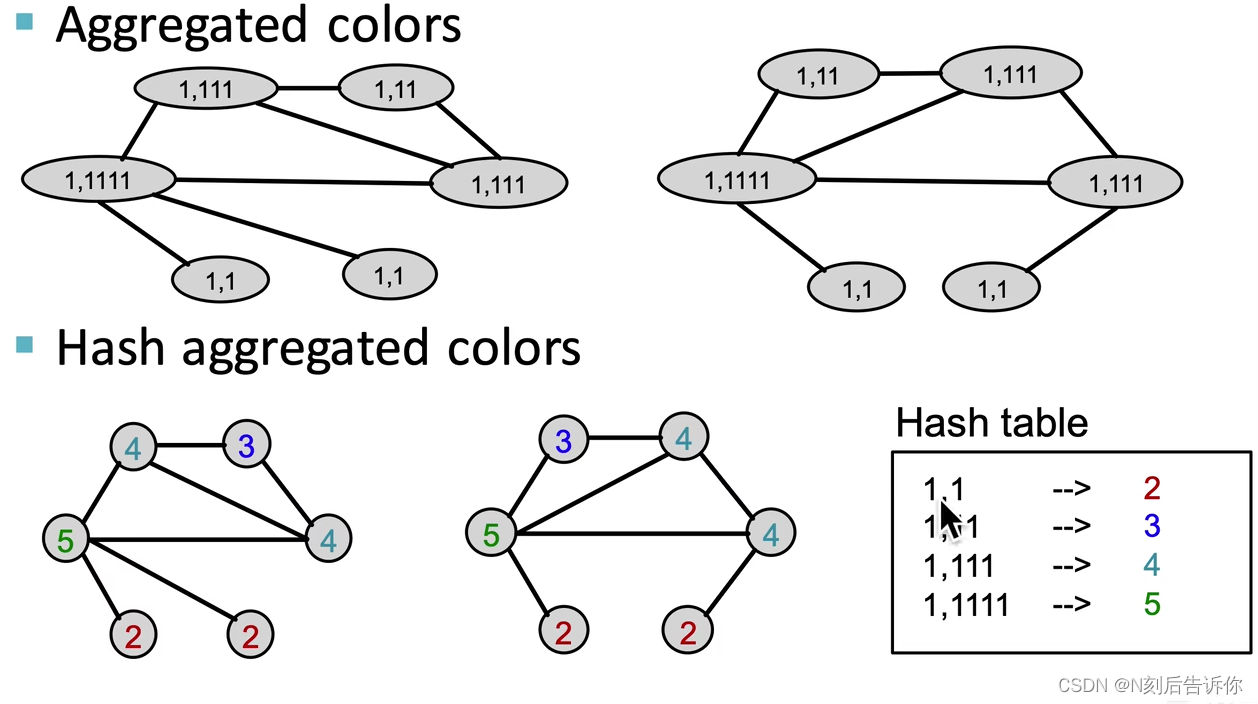
哈希表由两张图共同贡献
- 3.重复执行k次2的操作,获得 c ( K ) ( v ) c^{(K)}(v) c(K)(v),根据所有出现过的颜色,统计次数,得到 ϕ ( G ) \phi(G) ϕ(G)
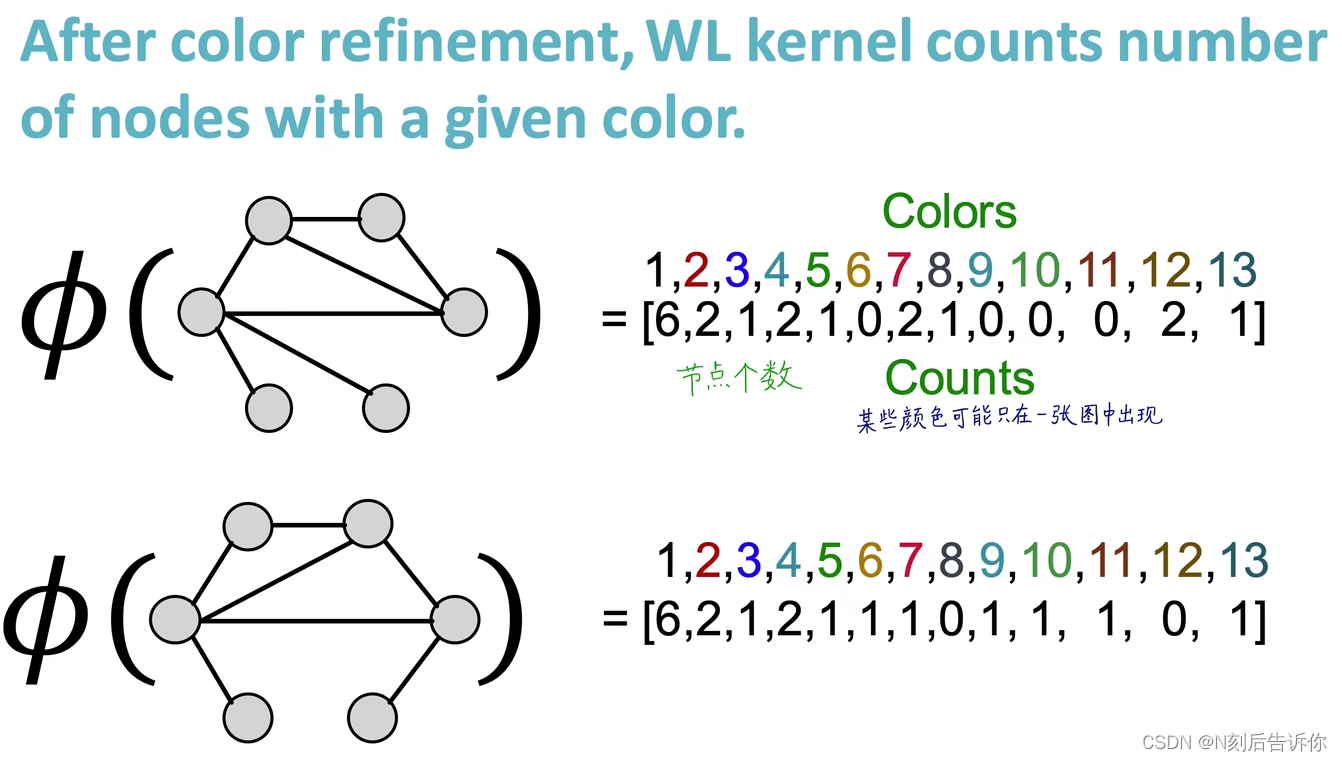
c ( K ) ( v ) c^{(K)}(v) c(K)(v)中包含了K跳邻域的信息。
- 4.计算WL Kernel: ϕ ( G ) T ϕ ( G ) \phi(G)^T\phi(G) ϕ(G)Tϕ(G)
总体而言,WL Kernel的时间复杂度是O(#(edges))。
kernel methods
核方法是传统技巧学习在图层面的预测的常用方法。它的核心是如何设计Kernel而非特征向量。
Kernel K ( G , G ′ ) K(G, G') K(G,G′)是标量,描述了数据间的相似度
核矩阵 K = ( K ( G , G ′ ) ) G , G ′ \boldsymbol{K}=\left(K\left(G, G^{\prime}\right)\right)_{G, G^{\prime}} K=(K(G,G′))G,G′永远半正定,即有正的特征值。
存在特征表示 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)使得 K ( G , G ′ ) = ϕ ( G ) T ϕ ( G ′ ) K\left(G, G^{\prime}\right)=\phi(G)^{\mathrm{T}} \phi\left(G^{\prime}\right) K(G,G′)=ϕ(G)Tϕ(G′)
一定kernel确定了,现成的机器学习模型,如Kernel SVM就可以用来预测。
Node Embeddings-图嵌入表示学习
图表示学习减轻了做特征工程的工作。
映射得到的向量具有低维(向量维度远小于节点数)、连续(每个元素都是实数)、稠密(每个元素都不为0)的特点。
图嵌入-基本框架:编码器-解码器
假设:G是图,V是节点集,A是无权图,本节仍仅考虑连接信息,不考虑节点信息。
目标是:节点编码后,两节点在嵌入空间中的向量的(余弦)相似度可以反应(近似)两节点在图中的相似度。即
s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v)\approx \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u similarity(u,v)≈zvTzu
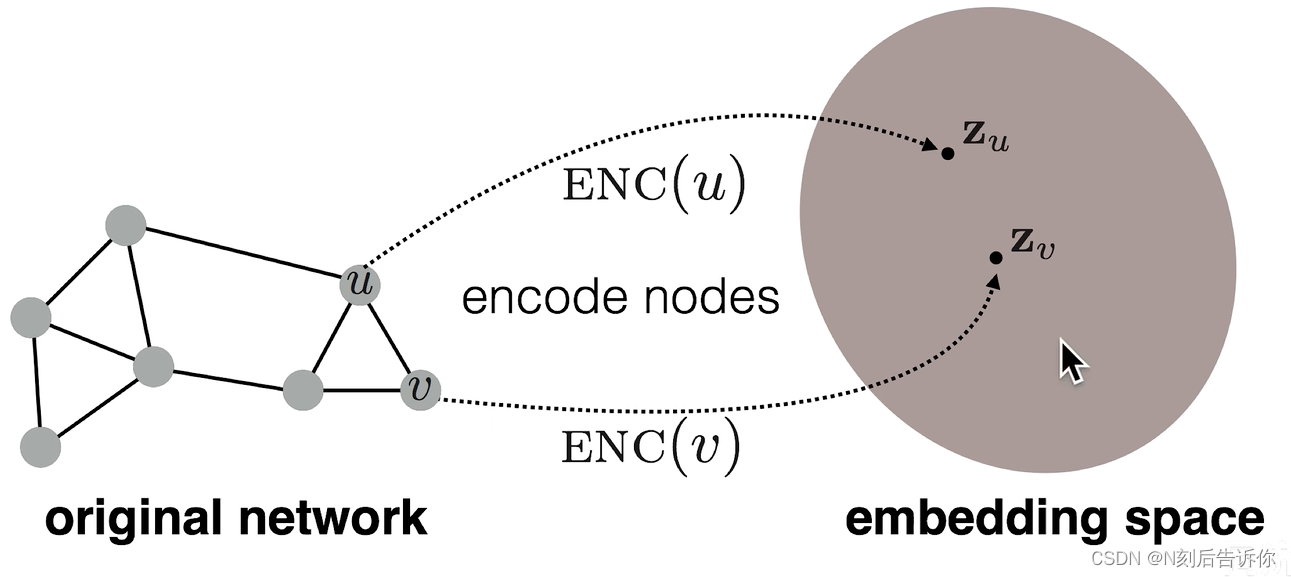
关键:如何定义节点的相似度。
步骤:
- 编码器:节点-》d维向量
- 定义节点在图中的相似度函数: s i m i l a r i t y ( u , v ) similarity(u,v) similarity(u,v)
- 解码器:计算两个节点向量的相似度:如 z v T z u \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u zvTzu
- 迭代优化编码器的参数使得图中相似节点的向量数量积大,不相似节点向量数量积小: s i m i l a r i t y ( u , v ) ≈ z v T z u similarity(u,v)\approx \mathbf{z}_v^{\mathrm{T}} \mathbf{z}_u similarity(u,v)≈zvTzu
node embeddings方法是无监督/自监督的,且与下游任务无关。
浅编码器
最简单的编码器-查表
只需要直接优化Z矩阵
对应方法有:DeepWalk,node2vec

基于随机游走的方法
图机器学习的很多概念可以类比NLP的很多概念
[暂时跳过这里去看DeepWalk论文精读]
相关文章:

[学习笔记]CS224W
资料: 课程网址 斯坦福CS224W图机器学习、图神经网络、知识图谱【同济子豪兄】 斯坦福大学CS224W图机器学习公开课-同济子豪兄中文精讲 图的基本表示 图是描述各种关联现象的通用语言。与传统数据分析中的样本服从独立同分布假设不一样,图数据自带关联…...
华为云API对话机器人CBS的魅力—实现简单的对话操作
云服务、API、SDK,调试,查看,我都行 阅读短文您可以学习到:人工智能AI智能的问答管理、全面的对话管理、高效训练部署 1.IntelliJ IDEA 之API插件介绍 API插件支持 VS Code IDE、IntelliJ IDEA等平台、以及华为云自研 CodeArts …...

精益制造、质量管控,盛虹百世慧共同启动MOM(制造运营管理)
百世慧科技依托在电池智能制造行业中的丰富经验,与盛虹动能达成合作,为其提供MOM制造运营管理平台,并以此为起点,全面提升盛虹动能的制造管理水平与运营体系。 行业困境 中国动力电池已然发展为全球最大的电池产业,但…...
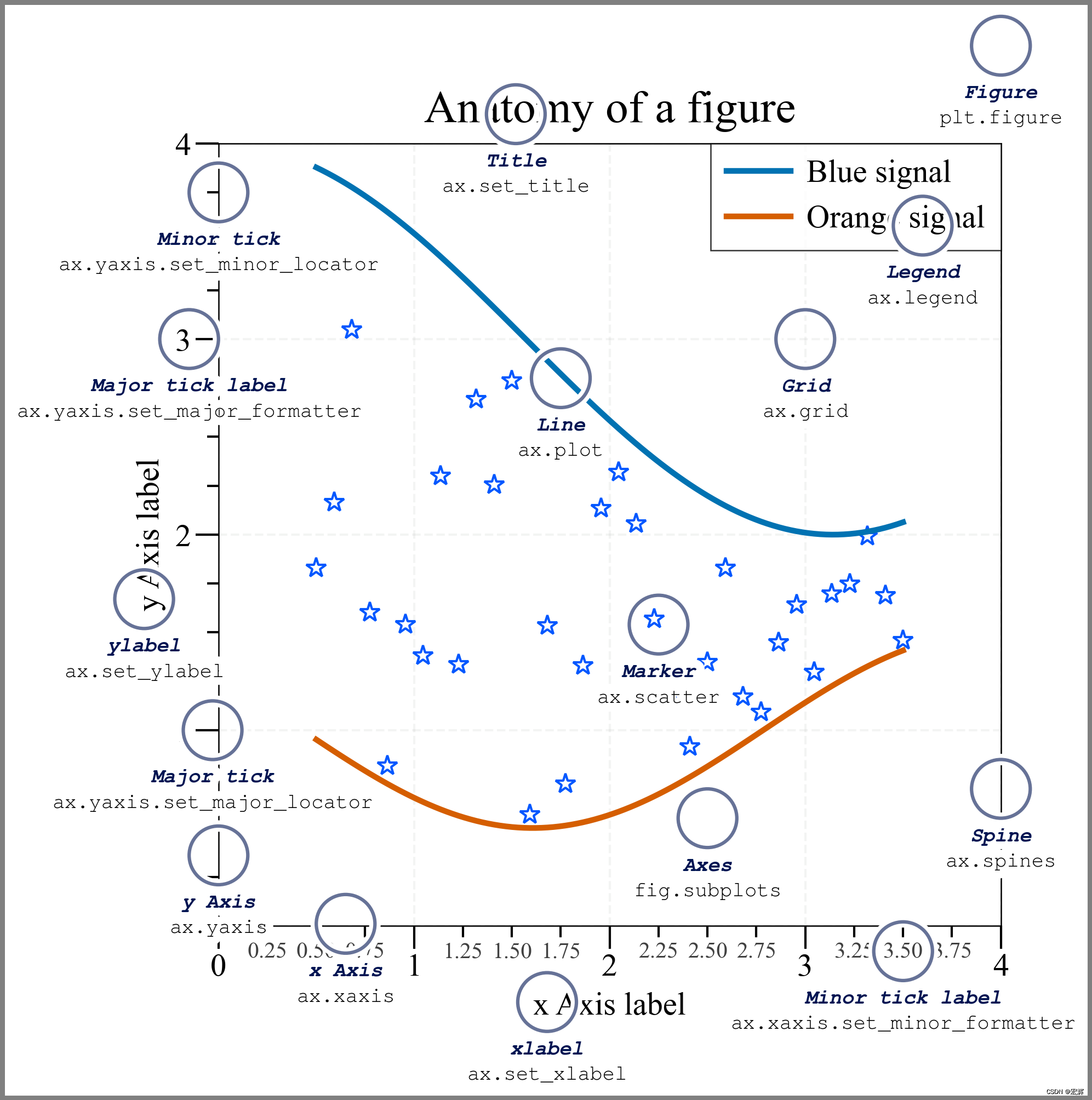
【科研论文配图绘制】task7密度图绘制
【科研论文配图绘制】task7密度图绘制 task7 了解密度图的定义,清楚密度图是常用使用常见,掌握密度图绘制。 1.什么是密度图 密度图(Density Plot)是一种用于可视化数据分布的图表类型。它通过在数据中创建平滑的概率密度曲线…...

Python3 集合
Python3 集合 集合(set)是一个无序的不重复元素序列。 可以使用大括号 { } 或者 set() 函数创建集合,注意:创建一个空集合必须用 set() 而不是 { },因为 { } 是用来创建一个空字典。 创建格式: parame …...

【山河送书第十期】:《Python 自动化办公应用大全》参与活动,送书两本!!
【山河送书第十期】:《Python 自动化办公应用大全》参与活动,送书两本!! 前言一书籍亮点二作者简介三内容简介四购买链接五参与方式六往期赠书回顾 前言 在过去的 5 年里,Python 已经 3 次获得 TIOBE 指数年度大奖&am…...

Java多线程——同步
同步是什么? 当两个线程同时对一个变量进行修改时,不同的访问顺序会造成不一样的结果,这时候就需要同步保证结果的唯一性。 未同步时 新建Bank类,transfer()用于在两个账户之间转账金额 class Bank {private double[] account…...
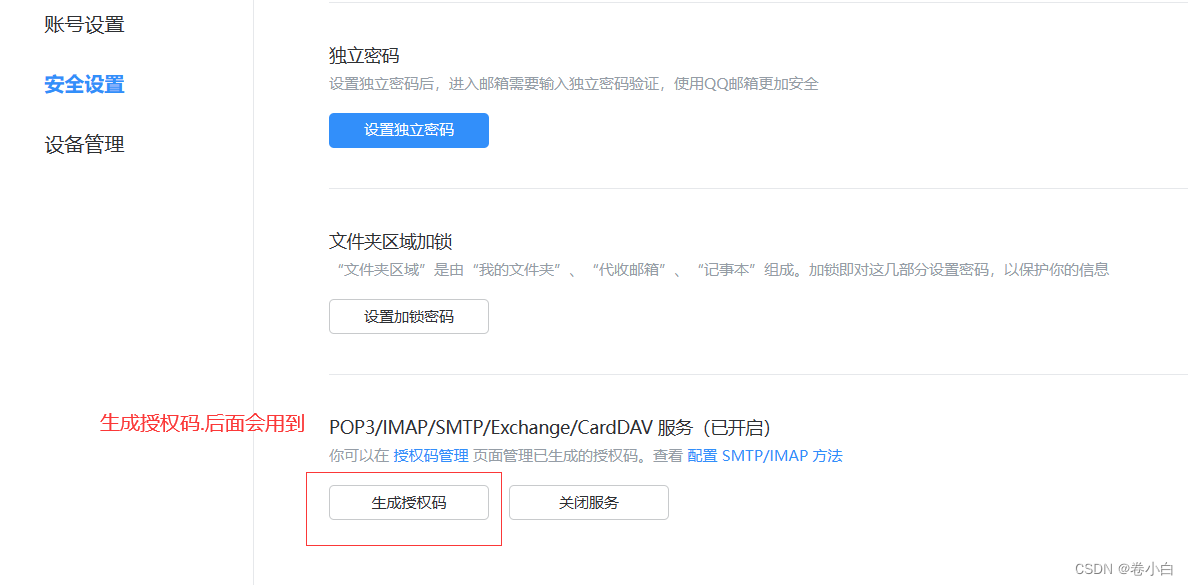
Vue+NodeJS实现邮件发送
一.邮箱配置 这里以QQ邮箱为例,网易邮箱类似. 设置->账号 二.后端服务搭建 index.js const express require(express) const router require(./router); const app express()// 使用路由文件 app.use(/,router);app.listen(3000, () > {console.log(server…...
TCP粘包)
Go语言网络编程(socket编程)TCP粘包
1、TCP粘包 服务端代码如下: // socket_stick/server/main.gofunc process(conn net.Conn) {defer conn.Close()reader : bufio.NewReader(conn)var buf [1024]bytefor {n, err : reader.Read(buf[:])if err io.EOF {break}if err ! nil {fmt.Println("read…...
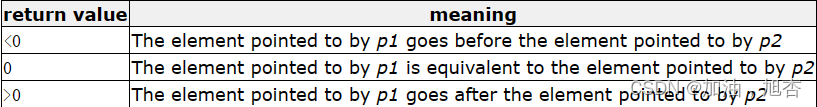
【再识C进阶2(中)】详细介绍指针的进阶——函数指针数组、回调函数、qsort函数
前言 💓作者简介: 加油,旭杏,目前大二,正在学习C,数据结构等👀 💓作者主页:加油,旭杏的主页👀 ⏩本文收录在:再识C进阶的专栏…...
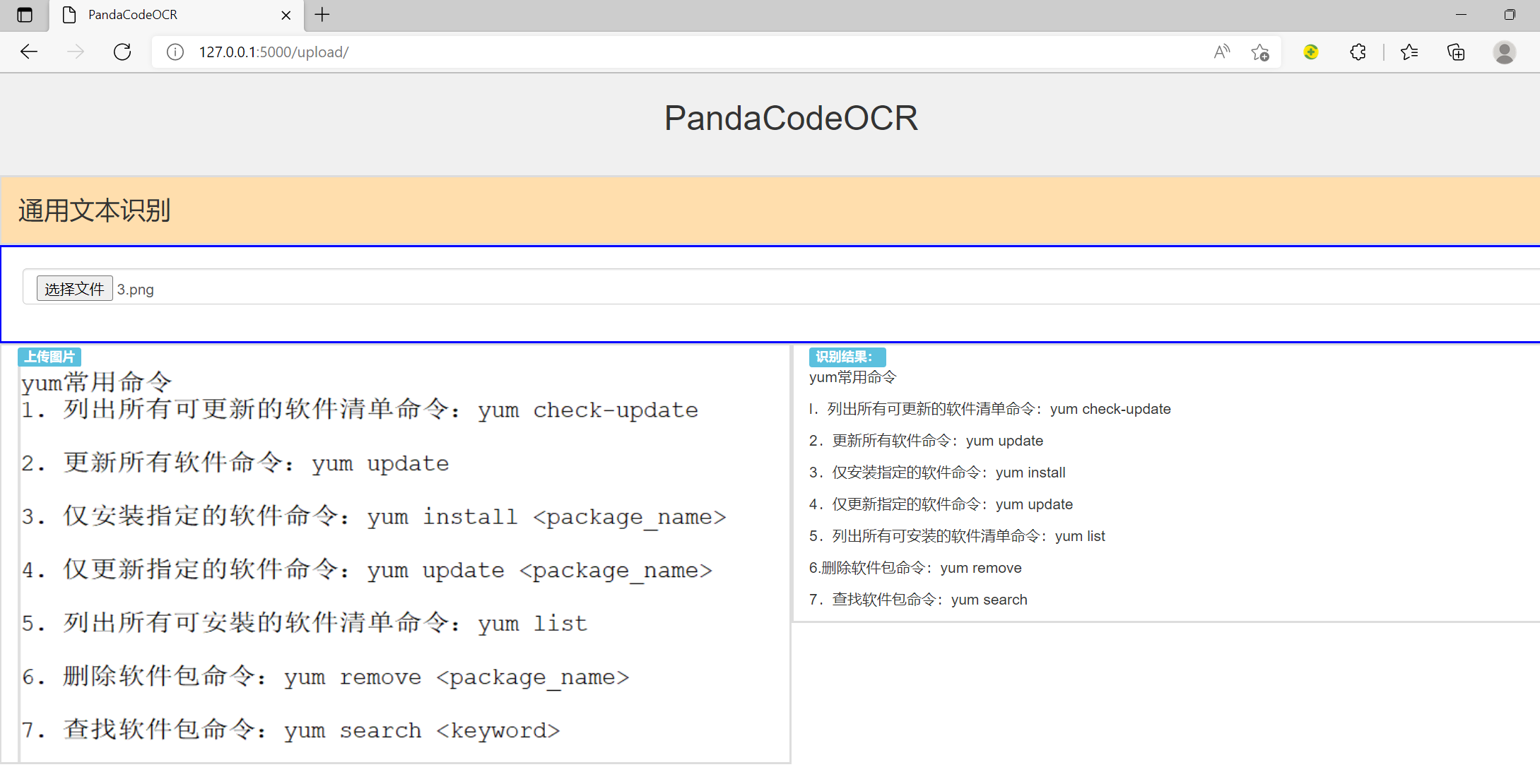
PaddleOCR学习笔记3-通用识别服务
今天优化了下之前的初步识别服务的python代码和html代码。 采用flask paddleocr bootstrap快速搭建OCR识别服务。 代码结构如下: 模板页面代码文件如下: upload.html : <!DOCTYPE html> <html> <meta charset"utf-8"> …...

9.8 校招 实习 内推 面经
绿泡*泡: neituijunsir 交流裙 ,内推/实习/校招汇总表格 1、校招 | 长安福特2024校园招聘正式启动 校招 | 长安福特2024校园招聘正式启动 2、2023校招总结--SLAM岗位 - 5 2023校招总结--SLAM岗位 - 5 3、校招&实习 | 格灵深瞳2024秋季校园招聘启…...

web前段与后端的区别优漫动游
要了解web前后端的区别,首先必须得清楚什么是web前端和web后端。 web前段与后端的区别 首先:web的本意是蜘蛛网和网的意思,在网页设计中我们称为网页的意思。现广泛译作网络、互联网等技术领域。表现为三种形式,即超文本(hyp…...
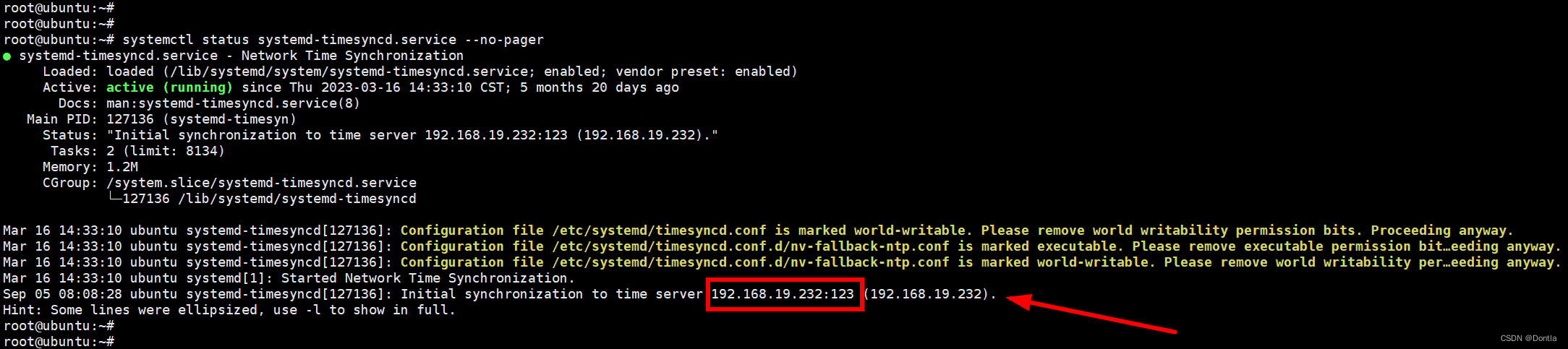
局域网ntp服务器设置(windows时间同步服务器NetTime)(ubuntu systemd-timesyncd ntp客户端)123端口、ntp校时
文章目录 背景windows如何配置ntp服务器手动配置配置参数AnnounceFlags和Enabled含义 使用软件配置(NetTime)实操相关疑问:0.nettime.pool.ntp.org是什么? 注意事项请务必检查windows主机123端口是否已被占用,方法请参…...

【个人博客系统网站】我的博客列表页 · 增删改我的博文 · 退出登录 · 博客详情页 · 多线程应用
【JavaEE】进阶 个人博客系统(4) 文章目录 【JavaEE】进阶 个人博客系统(4)1. 增加博文1.1 预期效果1.1 约定前后端交互接口1.2 后端代码1.3 前端代码1.4 测试 2. 我的博客列表页2.1 期待效果2.2 显示用户信息以及博客信息2.2.1…...

安全狗陈奋:数据安全需要建立在传统网络安全基础之上
8月22日-23日,由创业邦主办的“2023 DEMO WORLD 企业开放式创新大会”在上海顺利举行。 作为国内云原生安全领导厂商,安全狗受邀出席此次活动。 本次大会以“拥抱开放”为主题,聚焦开放式创新,通过演讲分享、专场对接、需求发布…...
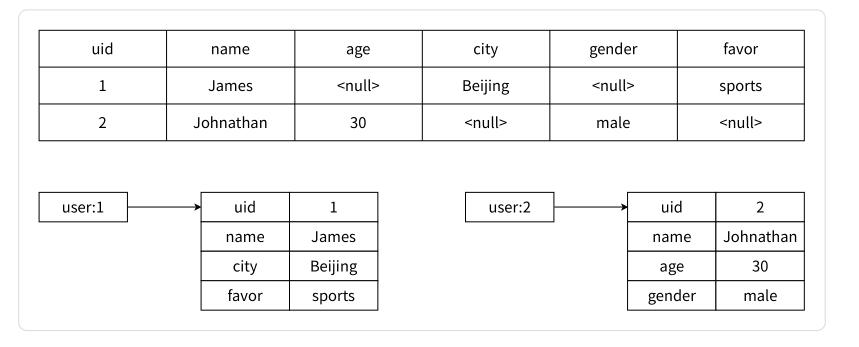
【Redis】深入探索 Redis 的数据类型 —— 哈希表 hash
文章目录 前言一、hash 类型相关命令1.1 HSET 和 HSETNX1.2 HGET 和 HMGET1.3 HKEYS、HVALS 和 HGETALL1.4 HEXISTS 和 HDEL1.5 HLEN1.6 HINCRBY 和 HINCRBYFLOAT1.7 哈希相关命令总结 二、hash 类型内部编码三、hash 类型的应用场景四、原生,序列化,哈希…...
)
网络安全应急响应典型案例-(DDOS类、僵尸网络类、数据泄露类)
一、DDOS类事件典型案例 DDOS攻击,即分布式拒绝服务攻击,其目的在于使目标电脑的网络或系统资源耗尽,使服务暂时中断或停止,导致其正常用户无法访问。CC攻击使用代理服务器向受害服务器发送大量貌似合法的请求(通常…...

【测试开发】Mq消息重复如何测试?
本篇文章主要讲述重复消费的原因,以及如何去测试这个场景,最后也会告诉大家,目前互联网项目关于如何避免重复消费的解决方案。 Mq为什么会有重复消费的问题? Mq 常见的缺点之一就是消息重复消费问题,产生这种问题的原因是什么呢…...

C++和C#程序语言的区别
一直学习C++和C#,两者之间的区别总结一下 目录 一、两种语言概述 C++语言 C#语言 二、两种语言对比 2.1运行依赖...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

MySQL 索引底层结构揭秘:B-Tree 与 B+Tree 的区别与应用
文章目录 一、背景知识:什么是 B-Tree 和 BTree? B-Tree(平衡多路查找树) BTree(B-Tree 的变种) 二、结构对比:一张图看懂 三、为什么 MySQL InnoDB 选择 BTree? 1. 范围查询更快 2…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...