王道数据结构编程题 查找
二叉树定义
以下为本文解题代码的二叉树定义。
struct TreeNode {int val;TreeNode* left, *right;TreeNode(int val = 0, TreeNode* left = nullptr, TreeNode* right = nullptr): val(val), left(left), right(right) {}
};
递归二分查找
题目描述
写出二分查找的递归算法。初始调用时,left 为1,right 为 n.
解题代码
bool recurBS(vector<int>& nums, int target, int left, int right) {if (left > right) return false;int mid = (left + right) / 2;if (nums[mid] == target) return true;else if (nums[mid] > target) {return recurBS(nums, target, left, mid - 1);}else {return recurBS(nums, target, mid + 1, right);}
}
优化顺序查找
题目描述
线性表中各结点的检索概率不等时,可用如下策略提高顺序检索的效率:若找到指定的结点,则将该结点和其前驱节点(若存在)交换,使得经常被检索的结点尽量位于表的前端。试设计在顺序结构和链式结构的线性表上实现上述策略的顺序检索算法。
解题代码
顺序表
bool optimisedSS(vector<int>& nums, int target) {for (int i = 0; i < nums.size(); ++i) {if (nums[i] == target) {if (i > 0) {swap(nums[i - 1], nums[i]);}return true;}}return false;
}
链表
bool optimisedSS(ListNode* head, int target) {if (head == nullptr) return false;ListNode* dummy = new ListNode(-1, head); // 哨兵结点if (dummy->next->val == target) return true;while (dummy->next->next != nullptr) {if (dummy->next->next->val == target) {ListNode* pre = dummy;ListNode* node1 = dummy->next;ListNode* node2 = dummy->next->next;pre->next = node2;node1->next = node2->next;node2->next = node1;return true;}dummy = dummy->next;}return false;
}
判定二叉搜索树
题目描述
试编写一个算法,判断给定的二叉树是否是二叉搜索树。
解题代码
bool dfs(TreeNode* root, int preVal) {if (root == nullptr) return true;if (!dfs(root->left, preVal) || root->val <= preVal) {return false;}preVal = root->val;return dfs(root->right, preVal);
}bool isBST(TreeNode* root) {int lastVal = INT32_MIN;return dfs(root, lastVal);
}
计算某结点层次
题目描述
设计一个算法,求出指定结点在给定二叉排序树中的层次。
解题代码
int dfs(TreeNode* root, TreeNode* node, int depth) {if (root == nullptr) return 0;if (root->val == node->val) {return depth;}else if (root->val < node->val) {return dfs(root->right, node, depth + 1);}else {return dfs(root->left, node, depth + 1);}
}int calNodeDepth(TreeNode* root, TreeNode* node) {return dfs(root, node, 1);
}
判定平衡二叉树
题目描述
利用二叉树遍历的遍历的思想,编写一个判断二叉树是否是平衡二叉树的算法。
解题代码
O(n^2)
int calDepth(TreeNode* root) {if (root == nullptr) return 0;return 1 + max(calDepth(root->left), calDepth(root->right));
}bool isBalanced(TreeNode* root) {if (root == nullptr) return true;int lDepth = calDepth(root->left);int rDepth = calDepth(root->right);return abs(lDepth - rDepth) <= 1 && isBalanced(root->left) && isBalanced(root->right);
}
在每次递归判断左右子树是否平衡时,需要重新计算其高度,因此引入了大量不必要的计算。而如果某棵树的子树之一已经是非平衡树,那么这棵树一定是非平衡树,根据该性质,可将对平衡的判断改为自底向上进行。以下为自底向上判断平衡的方式,可将时间复杂度优化至 O(n).
O(n)
int calDepth(TreeNode* root) {if (root == nullptr) return 0;int lDepth = calDepth(root->left);int rDepth = calDepth(root->right);if (lDepth == -1 || rDepth == -1 || abs(lDepth - rDepth) >= 2) {return -1;}return 1 + max(lDepth, rDepth);
}bool isBalanced(TreeNode* root) {return calDepth(root) >= 0;
}
二叉搜索树最大和最小结点
题目描述
设计一个算法,求出给定二叉搜索树中最小和最大的关键字。
解题代码
int calMaxVal(TreeNode* root) {if (root->right == nullptr) return root->val;return calMaxVal(root->right);
}int calMinVal(TreeNode* root) {if (root->left == nullptr) return root->val;return calMinVal(root->left);
}pair<int, int> calMaxMin(TreeNode* root) {int minVal = root->left == nullptr ? root->val : calMinVal(root->left);int maxVal = root->right == nullptr ? root->val : calMaxVal(root->right);return make_pair(minVal, maxVal);
}
二叉搜索树值不小于 k 的元素
题目描述
设计一个算法,从大到小输出二叉搜索树中所有值不小于 k 的元素。
解题代码
void printNotSmallerK(TreeNode* root, int k) {if (root == nullptr) return;printNotSmallerK(root->right, k);if (root->val >= k) {cout << root->val << " ";}else return;printNotSmallerK(root->left, k);
}
查找第k小的元素
题目描述
编写一个递归算法,在一棵有 n 个结点的,随机建立起来的二叉搜索树上查找第 k (1 <= k <= n)小的元素,并返回指向该结点的指针,要求算法的平均时间复杂度为 O(logn)。二叉搜索树中的每个结点除 data, lchild, rchild 等数据成员外,增加一个 count 成员,保存以该结点为根的子树上的结点个数。
解题代码
TreeNode* findKthNode(TreeNode* root, int& k) {if (root == nullptr) return nullptr;TreeNode* left = findKthNode(root->left, k);if (left != nullptr) return left;if (--k == 0) return root;return findKthNode(root->right, k);
}
相关文章:

王道数据结构编程题 查找
二叉树定义 以下为本文解题代码的二叉树定义。 struct TreeNode {int val;TreeNode* left, *right;TreeNode(int val 0, TreeNode* left nullptr, TreeNode* right nullptr): val(val), left(left), right(right) {} };递归二分查找 题目描述 写出二分查找的递归算法。初…...

vue 部分知识点总结
计算属性和方法有什么区别,怎么选择? 在编程中,计算属性和方法都是用于处理数据的工具,但它们有一些区别。以下是它们的区别和如何选择的几个因素: 执行方式:计算属性是基于依赖的响应式系统,在…...

谷粒商城----ES篇
一、product-es准备 P128 ES在内存中,所以在检索中优于mysql。ES也支持集群,数据分片存储。 需求: 上架的商品才可以在网站展示。上架的商品需要可以被检索。 分析sku在es中如何存储 商品mapping 分析:商品上架在es中是存s…...
Redis3.2.1如何设置远程连接?允许局域网访问
背景: 电脑A的redis需要开放给电脑B使用,二者处于同一局域网 【后面会补充更详细的踩坑历程,先发出来作为记录】 过程: 在你查了很多方法后,如果还是没有解决, 尝试考虑一下你的redis配置文件是不是修…...

网络原理(二)TCP的可靠传输
网络原理(一)目录 网络原理应用层传输层先说UDP(不可靠传输)重点说明TCP(可靠传输)一、确认应答二、超时重传三、链接管理建立连接断开链接 四、滑动窗口五、流量控制&am…...

Chat GPT 使用教学,文字创作、学习
目录 文章长篇文章学习任何东西文章 大纲、目录、标题、内容 写出10个即将被AI取代的工作的文章标题 当然,以下是一些可能会被AI取代的工作的文章标题:"未来十年,AI将如何改变传统制造业的就业格局?" "智能客服崛起:人工智能如何重塑客户服务行业?"…...

Android之 Canvas绘制
一 Canvas介绍 1.1 Canvas 是绘制图形的重要类之一,它可以在 View 或 SurfaceView 上绘制各种图形和文本. 1.2 要创建 Canvas,首先需要有一个 View 或 SurfaceView 对象,在 View 或 SurfaceView 的绘制方法中,可以通过 Canvas 的…...
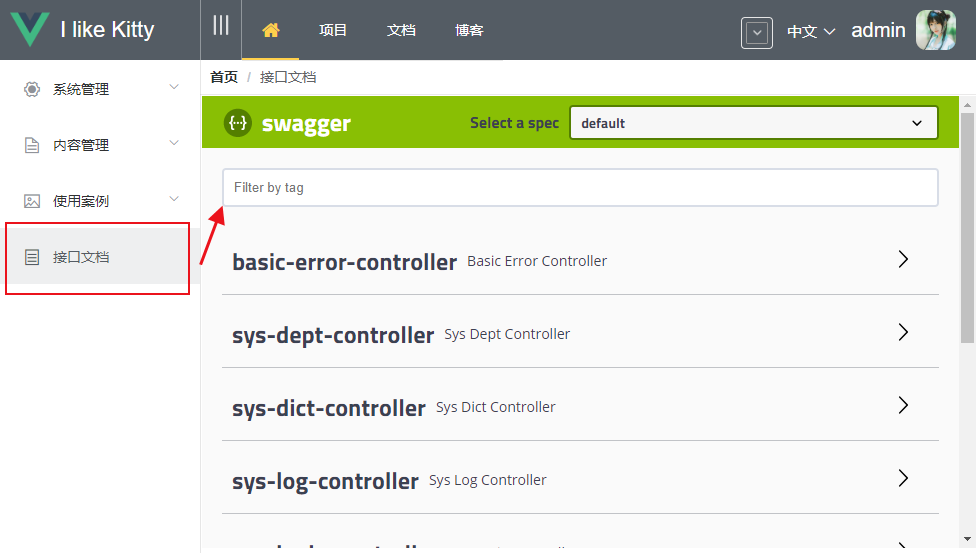
Vue + Element UI 前端篇(十五):嵌套外部网页
Vue Element UI 实现权限管理系统 前端篇(十五):嵌套外部网页 嵌套外部网页 在有些时候,我们需要在我们的内容栏主区域显示外部网页。如查看服务端提供的SQL监控页面,接口文档页面等。 这个时候就要求我们的导航菜…...
)
Jabbi的Rust学习日记(二)
特征: 就目前我学习到的rust知识来看,我认为rust有以下几个特征: 链式调用表达式强类型 use 使用use导入包,我觉得rust的导包和python的很像 main main函数是rust可执行程序最先执行的代码,可以说是程序的入口&…...
【杂】环形时钟配色笔记
配色网站笔记 coolorsflatuicolorscolordrophttps://www.webdesignrankings.com/resources/lolcolors/ 配色2...

会话跟踪技术学习笔记(Cookie+Session)+ HTTP学习笔记
一、核心知识点(重点): 1.1 Cookie 1. Cookie:是一种客户端会话技术,数据会被保存在客户端,Cookie会携带数据访问服务器,用以完成一次会话内多次请求间的数据共享 2. 过程:浏览器…...

分类预测 | MATLAB实现PCA-BiLSTM(主成分双向长短期记忆神经网络)分类预测
分类预测 | MATLAB实现PCA-BiLSTM(主成分双向长短期记忆神经网络)分类预测 目录 分类预测 | MATLAB实现PCA-BiLSTM(主成分双向长短期记忆神经网络)分类预测预测效果基本介绍程序设计参考资料致谢 预测效果 基本介绍 分类预测 | MATLAB实现PCA-BiLSTM(主成分双向长短期记忆神经网…...

Yarn 和 npm 的区别
Yarn 和 npm 都是 JavaScript 的包管理工具,它们的主要区别在于以下几个方面: 性能:Yarn 的安装速度和包的下载速度通常比 npm 更快,这是因为 Yarn 使用本地缓存和并行下载等技术来提高性能。 可靠性:Yarn 具有更好的…...

第20章 原子操作实验(iTOP-RK3568开发板驱动开发指南 )
在上一章节的实验中,对并发与竞争进行了实验,两个app应用程序之间对共享资源的竞争访问引起了数据传输错误,而在Linux内核中,提供了四种处理并发与竞争的常见方法,分别是原子操作、自旋锁、信号量、互斥体,…...

Android 开机自启动
APP需要开机自启动,要通过开机广播实现。 1,在AndroidManifest.xml中增加权限 <!-- .接收启动完成的广播权限 --><uses-permission android:name"android.permission.RECEIVE_BOOT_COMPLETED" /> 2,在AndroidManifes…...

01_前端css编写的三种方式
前言 CSS的引入方式共有三种:行内样式、内部样式表、外部样式表 一、内联式引入 用法: 在元素上直接通过style属性进行设置css样式设置 示例: <h1 style"color:red;">style属性的应用</h1> <p style"font-si…...

07-垃圾收集算法详解
上一篇:06-JVM对象内存回收机制深度剖析 1.分代收集理论 当前虚拟机的垃圾收集都采用分代收集算法,这种算法没有什么新的思想,只是根据对象存活周期的不同将内存分为几块。一般将java堆分为新生代和老年代,这样我们就可以根据各…...

Redis高并发分布式锁实战
高并发场景秒杀抢购超卖bug实战重现 秒杀抢购场景下实战JVM级别锁与分布式锁 大厂分布式锁Resisson框架实战 Lua脚本语言快速入门与使用注意事项 Redisson分布式锁源码剖析 Redis主从架构锁失效问题解析 从CAP角度剖析Redis与Zookeeper分布式锁区别 Redlock分布式锁原理与…...
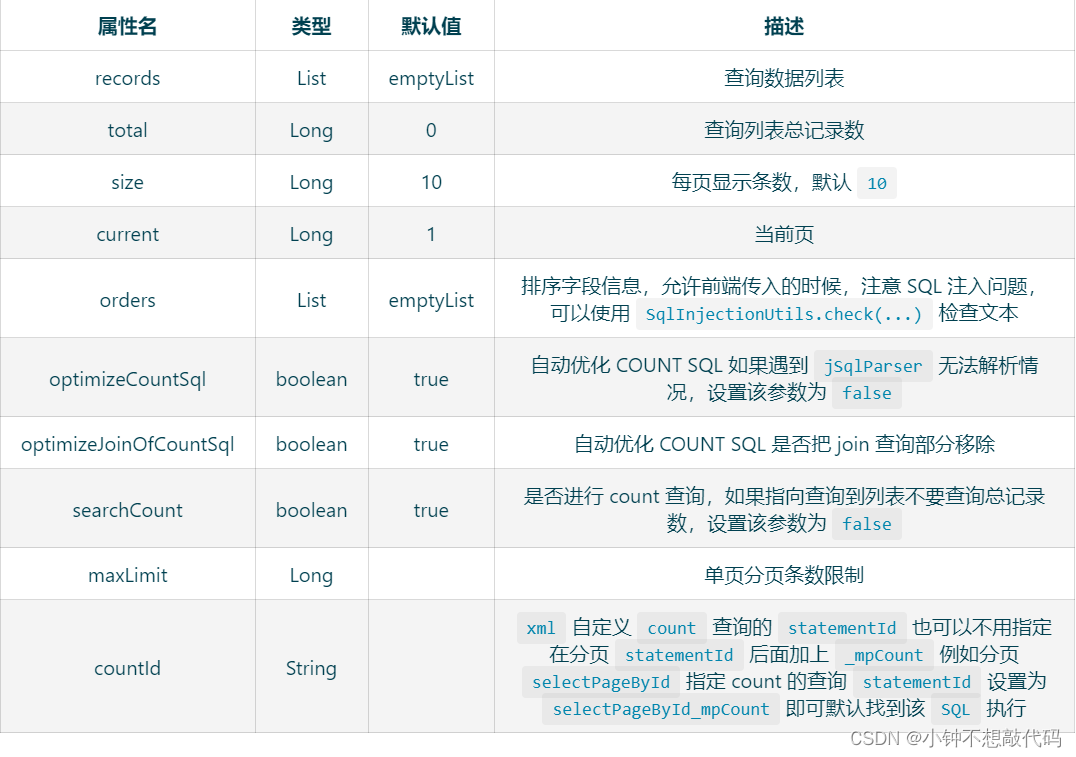
MybatisPlus分页插件使用
一. 效果展示 二. 代码编写 2.1 pom <dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-boot-starter</artifactId><version>3.4.2</version> </dependency>2.2 添加配置类 Configuration MapperScan(…...

Linux指令二【进程,权限,文件】
进程是一个具有一定独立功能的程序在一个数据集上的一次动态执行的过程,是操作系统进行 资源分配和调度的一个独立单位,是应用程序运行的载体。 一、进程基本指令 1.ps:当前的用户进程 ps 只显示隶属于自己的进程状态ps -aux 显示所有进程…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
