机器学习实战-系列教程5:手撕线性回归4之非线性回归(项目实战、原理解读、源码解读)
🌈🌈🌈机器学习 实战系列 总目录
本篇文章的代码运行界面均在Pycharm中进行
本篇文章配套的代码资源已经上传
手撕线性回归1之线性回归类的实现
手撕线性回归2之单特征线性回归
手撕线性回归3之多特征线性回归
手撕线性回归4之非线性回归
11、非线性模型
当得到一个回归方程会,得到一条直线来拟合这个数据的统计规律,但是实际中用这样的简单直线很显然并不能拟合出统计规律,所谓线性回归比如两个变量之间关系就直接用一条直线来拟合,2个变量和一个1个变量的关系就用一个平面来拟合。在数学就是一个一元一次和多元一次函数的映射。非线性就是有多次,也就是说不再是一个直线了,可能是二次或者更高,也可以用三角函数来进行非线性变换。
11.1 读入数据
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from linear_regression import LinearRegression
data = pd.read_csv('../data/non-linear-regression-x-y.csv')
x = data['x'].values.reshape((data.shape[0], 1))
y = data['y'].values.reshape((data.shape[0], 1))
data.head(10)
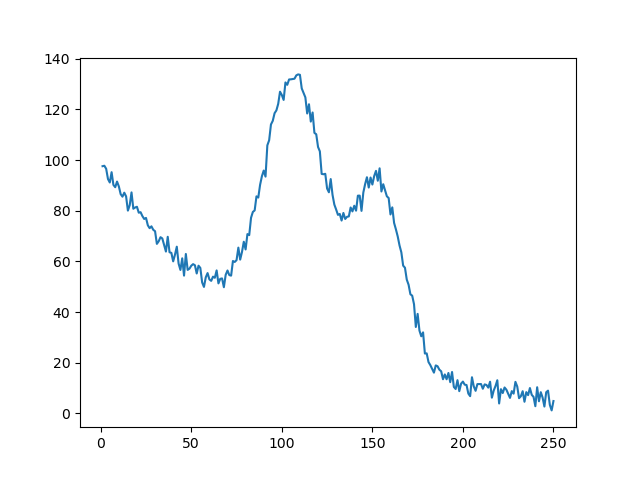
plt.plot(x, y)
plt.show()
- 导包
- 读入数据
- 得到x数据
- 得到y数据
- 取前10个
- 将x和y画图
打印结果:
11.2 多项式非线性变换函数
polynomial_degree是一个下面generate_polynomials这个多项式函数需要设置的参数
不同的参数产生的数据是怎样的呢?
如有一个数据[a,b]:
当degree=1时,kernel变换后的数据(仅为增加一个偏置项) 为:[1,a,b]
当degree=2时,kernel变换后的数据为:[1,a,b, a 2 a^2 a2,ab, b 2 b^2 b2]
当degree=3时,kernel变换后的数据为:[1,a,b, a 2 a^2 a2,ab, b 2 , a 2 b , a b 2 , a 3 , b 3 b^2,a^2b,ab^2,a^3,b^3 b2,a2b,ab2,a3,b3]
以此类推
import numpy as np
from .normalize import normalize
def generate_polynomials(dataset, polynomial_degree, normalize_data=False):features_split = np.array_split(dataset, 2, axis=1)dataset_1 = features_split[0]dataset_2 = features_split[1](num_examples_1, num_features_1) = dataset_1.shape(num_examples_2, num_features_2) = dataset_2.shapeif num_examples_1 != num_examples_2:raise ValueError('Can not generate polynomials for two sets with different number of rows')if num_features_1 == 0 and num_features_2 == 0:raise ValueError('Can not generate polynomials for two sets with no columns')if num_features_1 == 0:dataset_1 = dataset_2elif num_features_2 == 0:dataset_2 = dataset_1num_features = num_features_1 if num_features_1 < num_examples_2 else num_features_2dataset_1 = dataset_1[:, :num_features]dataset_2 = dataset_2[:, :num_features]polynomials = np.empty((num_examples_1, 0))for i in range(1, polynomial_degree + 1):for j in range(i + 1):polynomial_feature = (dataset_1 ** (i - j)) * (dataset_2 ** j)polynomials = np.concatenate((polynomials, polynomial_feature), axis=1)if normalize_data:polynomials = normalize(polynomials)[0]return polynomials
11.3 三角函数非线性变换函数
import numpy as np
def generate_sinusoids(dataset, sinusoid_degree):num_examples = dataset.shape[0]sinusoids = np.empty((num_examples, 0))for degree in range(1, sinusoid_degree + 1):sinusoid_features = np.sin(degree * dataset)sinusoids = np.concatenate((sinusoids, sinusoid_features), axis=1) return sinusoids
11.4 执行线性回归
num_iterations = 50000
learning_rate = 0.02
polynomial_degree = 15
sinusoid_degree = 15
normalize_data = True
linear_regression = LinearRegression(x, y, polynomial_degree, sinusoid_degree, normalize_data)
(theta, cost_history) = linear_regression.train( learning_rate, num_iterations)
print('开始损失: {:.2f}'.format(cost_history[0]))
print('结束损失: {:.2f}'.format(cost_history[-1]))
- 迭代次数
- 学习率
- 多项式次数
- 三角函数次数
- 类实例化成对象
- 执行train函数和之前一样
- 打印损失
打印结果:
开始损失: 2274.66
结束损失: 35.04
11.5 损失变化过程
theta_table = pd.DataFrame({'Model Parameters': theta.flatten()})plt.plot(range(num_iterations), cost_history)
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.title('Gradient Descent Progress')
plt.show()
这里和之前的过程是一样的,打印结果:
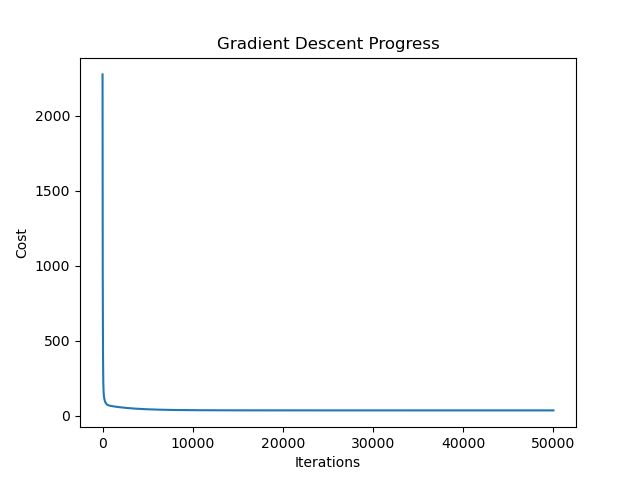
这里的损失在很早的时候就已经下降的很低了,因为次数设置的过大导致模型过拟合了
11.6 回归线
predictions_num = 1000
x_predictions = np.linspace(x.min(), x.max(), predictions_num).reshape(predictions_num, 1);
y_predictions = linear_regression.predict(x_predictions)
plt.scatter(x, y, label='Training Dataset')
plt.plot(x_predictions, y_predictions, 'r', label='Prediction')
plt.show()
这里的回归线实现过程还是和之前的一样,打印结果:
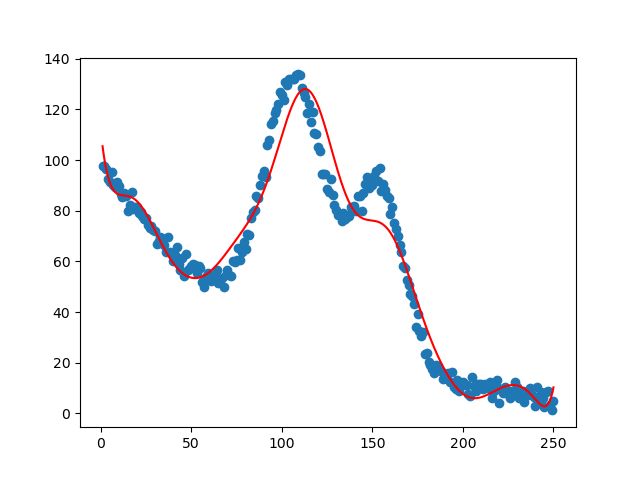
这就是用非线性回归实现的最后曲线拟合的结果
手撕线性回归1之线性回归类的实现
手撕线性回归2之单特征线性回归
手撕线性回归3之多特征线性回归
手撕线性回归4之非线性回归
相关文章:

机器学习实战-系列教程5:手撕线性回归4之非线性回归(项目实战、原理解读、源码解读)
🌈🌈🌈机器学习 实战系列 总目录 本篇文章的代码运行界面均在Pycharm中进行 本篇文章配套的代码资源已经上传 手撕线性回归1之线性回归类的实现 手撕线性回归2之单特征线性回归 手撕线性回归3之多特征线性回归 手撕线性回归4之非线性回归 1…...

【C语言基础】那些你可能不知道的C语言“潜规则”
📢:如果你也对机器人、人工智能感兴趣,看来我们志同道合✨ 📢:不妨浏览一下我的博客主页【https://blog.csdn.net/weixin_51244852】 📢:文章若有幸对你有帮助,可点赞 👍…...
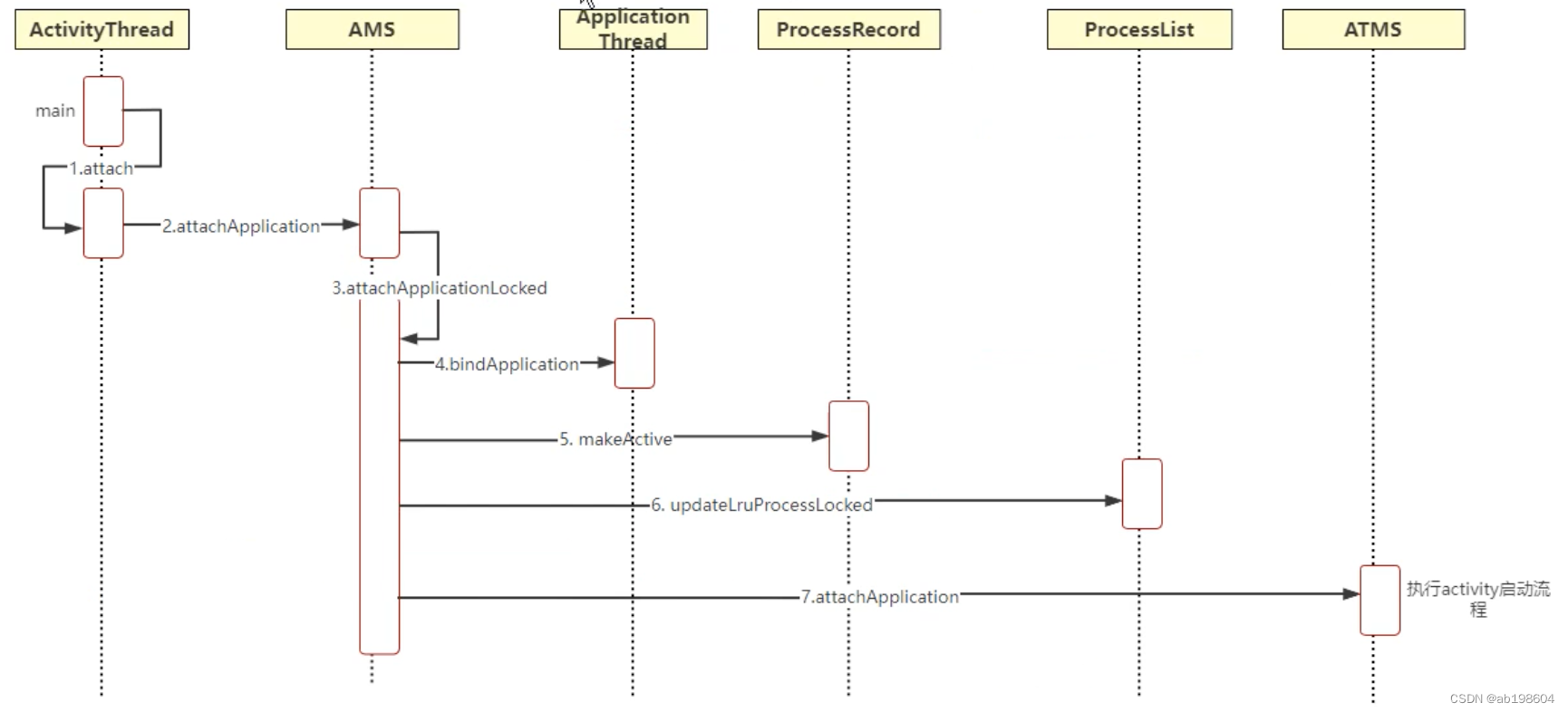
android framework之Applicataion启动流程分析(三)
现在再回顾一下Application的启动流程,总的来说,虽然进程的发起是由ATMS服务发起的,但是进程的启动还是由AMS负责,所以需要调用AMS的startProcess()接口完成进程启动流程,AMS要处理的事情很多,它将事务交给…...

使用Scrapy框架集成Selenium实现高效爬虫
引言: 在网络爬虫的开发中,有时候我们需要处理一些JavaScript动态生成的内容或进行一些复杂的操作,这时候传统的基于请求和响应的爬虫框架就显得力不从心了。为了解决这个问题,我们可以使用Scrapy框架集成Selenium来实现高效的爬…...

Maven 和 Gradle 官方文档及相关资料的网址集合
文章目录 官方MavenGradle 笔者MavenGradle 官方 Maven Maven 仓库依赖包官方查询通道:https://mvnrepository.com/ Maven 插件官方文档:https://maven.apache.org/plugins/ 安卓依赖包官方查询通道*:https://maven.google.com/web/ Gra…...
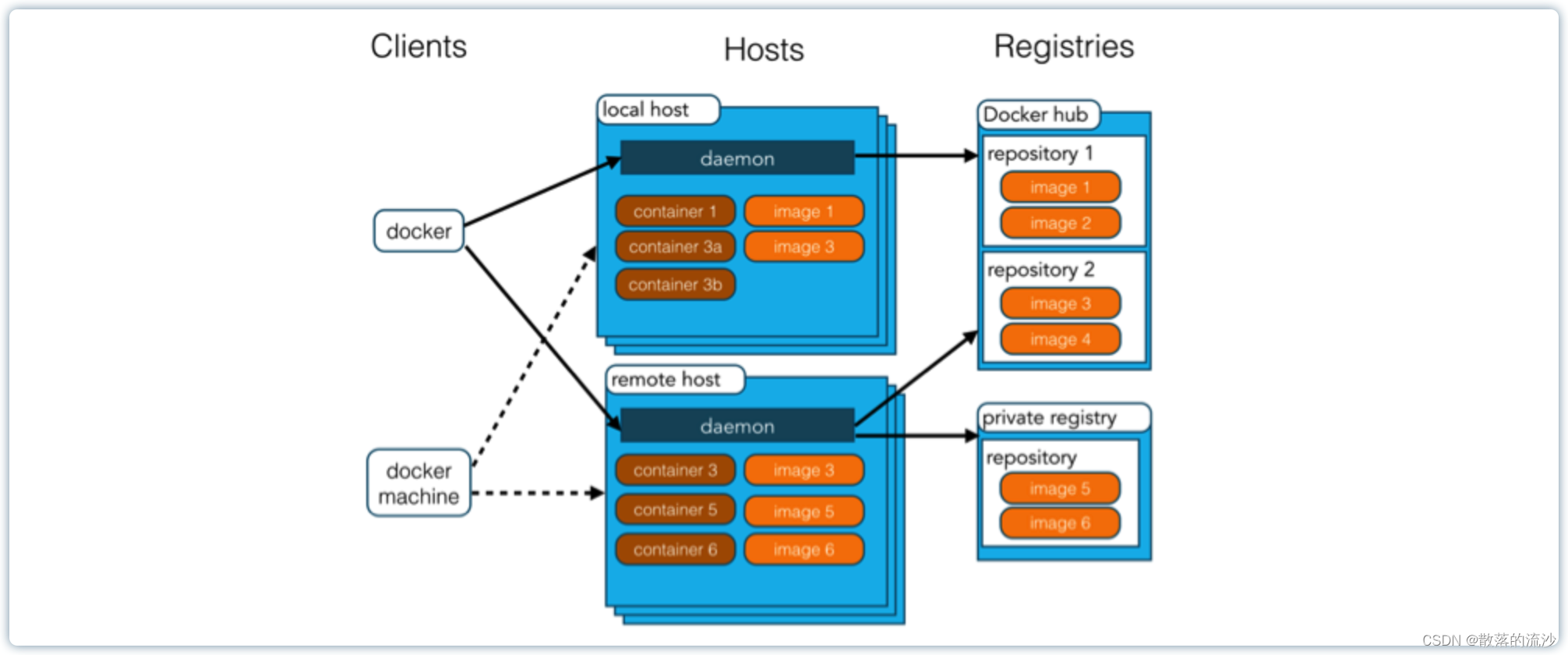
docker概念、安装与卸载
第一章 docker概念 Docker 是一个开源的应用容器引擎。 Docker 诞生于2013年初,基于 Go 语言实现,dotCloud 公司出品,后改名为 Docker Inc。 Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发…...
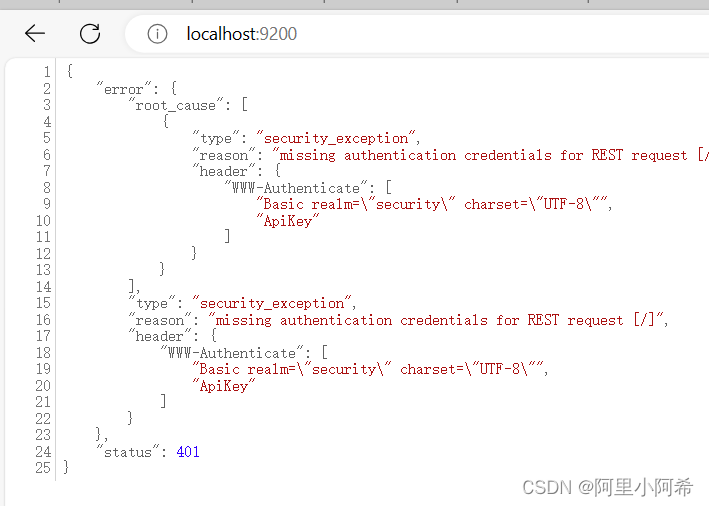
elasticsearch访问9200端口 提示需要登陆
项目场景: 提示:这里简述项目相关背景: elasticsearch访问9200端口 提示需要登陆 问题描述 提示:这里描述项目中遇到的问题: 在E:\elasticsearch-8.9.1-windows-x86_64\elasticsearch-8.9.1\bin目录下输入命令 ela…...
:Python基本数据类型:1、数字(整数、浮点数)及相关运算;2、布尔值)
【深度学习】 Python 和 NumPy 系列教程(一):Python基本数据类型:1、数字(整数、浮点数)及相关运算;2、布尔值
目录 一、前言 二、实验环境 三、Python基本数据类型 1. 数字 a. 整数(int) b. 浮点数(float) c. 运算 运算符 增强操作符 代码整合 d. 运算中的类型转换 e. 运算函数abs、max、min、int、float 2. 布尔值(…...
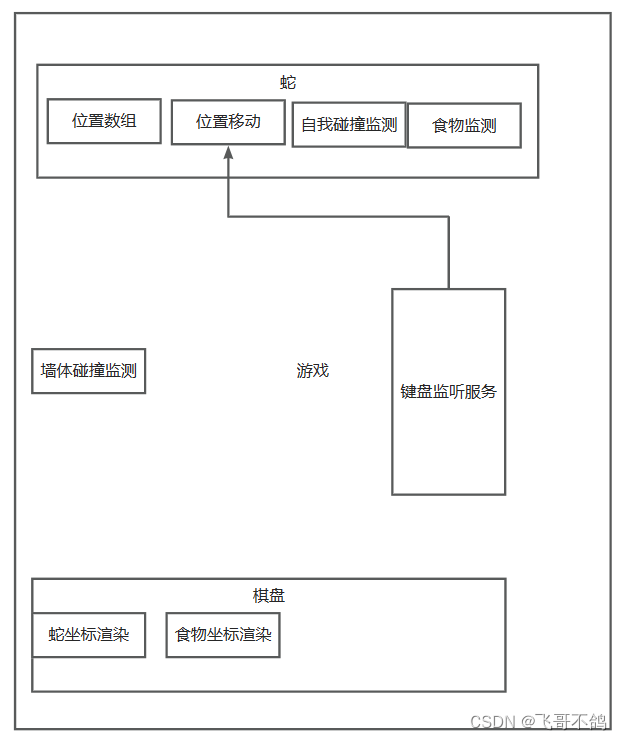
无swing,高级javaSE毕业之贪吃蛇游戏(含模块构建,多线程监听服务)
JavaSE,无框架实现贪吃蛇 文章目录 JavaSE,无框架实现贪吃蛇1.整体思考2.可能的难点思考2.1 如何表示游戏界面2.2 如何渲染游戏界面2.3 如何让游戏动起来2.4 蛇如何移动 3.流程图制作4.模块划分5.模块完善5.0常量优化5.1监听键盘服务i.输入存储ii.键盘监…...
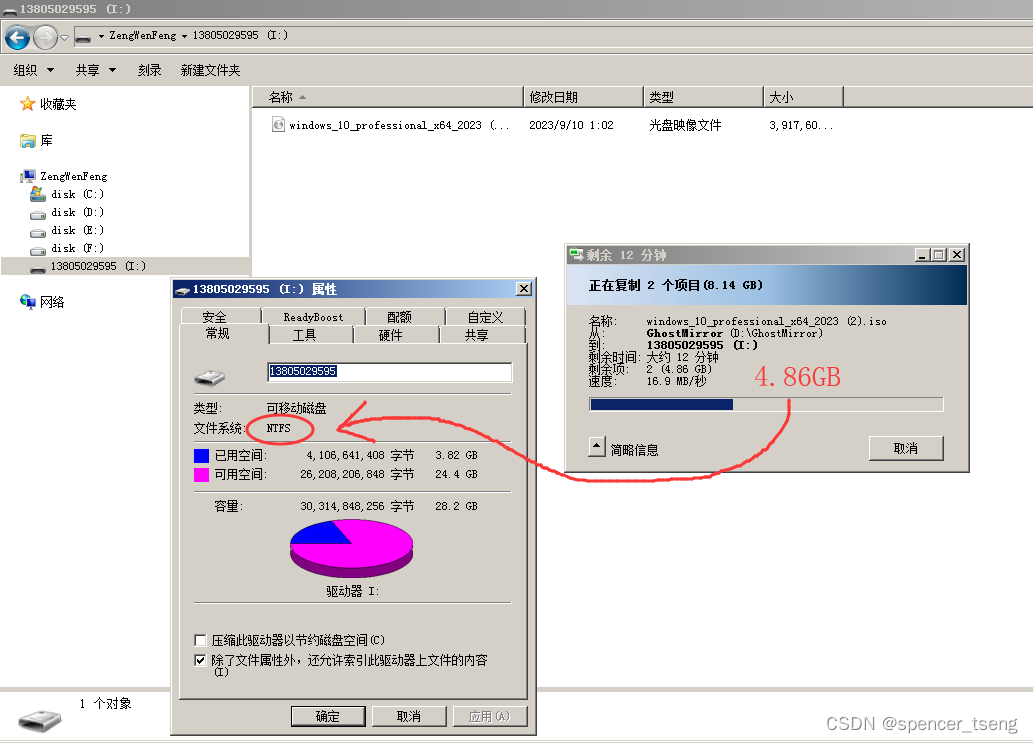
HDD-FAT32 ZIP-FAT32 HDD-FAT16 ZIP-FAT16 HDD-NTFS
FAT32、FAT16指的是分区格式, FAT16单个文件最大2G FAT32单个文件最大4G NTFS单个文件大于4G HDD是硬盘启动 ZIP是软盘启动 U盘选HDD HDD-NTFS...

王道数据结构编程题 二叉树
二叉树定义 以下为本文解题代码的二叉树定义。 struct TreeNode {int val;TreeNode* left, *right;TreeNode(int val 0, TreeNode* left nullptr, TreeNode* right nullptr): val(val), left(left), right(right) {} };非递归后序遍历 题目描述 编写后序遍历二叉树的非递…...

登录怎么实现的,密码加密了嘛?使用明文还是暗文,知道怎么加密嘛?
在Java中登录功能的实现通常包括以下步骤,其中密码应该以加密形式存储在数据库中,而不以明文形式存储,以增强安全性: 登录功能的实现步骤: 用户输入: 用户在登录页面上输入用户名和密码。 传输到服务器&a…...

Nginx和Tomcat负载均衡实现session共享
以前的项目使用Nginx作为反向代理实现了多个Tomcat的负载均衡,为了实现多个Tomcat之间的session共享,使用了开源的Memcached-Session-Manager框架。 此框架的优势: 1、支持Tomcat6和Tomcat7 2、操作粘性或不黏性Session 3、没有单点故障 4、T…...

【算法题】210. 课程表 II
题目: 现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。给你一个数组 prerequisites ,其中 prerequisites[i] [ai, bi] ,表示在选修课程 ai 前 必须 先选修 bi 。 例如,想要学习课程 0 ,…...

“数据类型不一致”会走索引吗?
分析&回答 字符串类型的索引 id_1 varchar(20) NOT NULL这样下面两条语句的结果是一样的: SELECT * FROM ix_test WHERE id_11; SELECT * FROM ix_test WHERE id_11;执行计划是不同的: mysql> explain select * from ix_test where id_11; | 1 …...

Leetcode 1572.矩阵对角线元素之和
给你一个正方形矩阵 mat,请你返回矩阵对角线元素的和。 请你返回在矩阵主对角线上的元素和副对角线上且不在主对角线上元素的和。 示例 1: 输入:mat [[1,2,3],[4,5,6],[7,8,9]] 输出:25 解释:对角线的和为ÿ…...
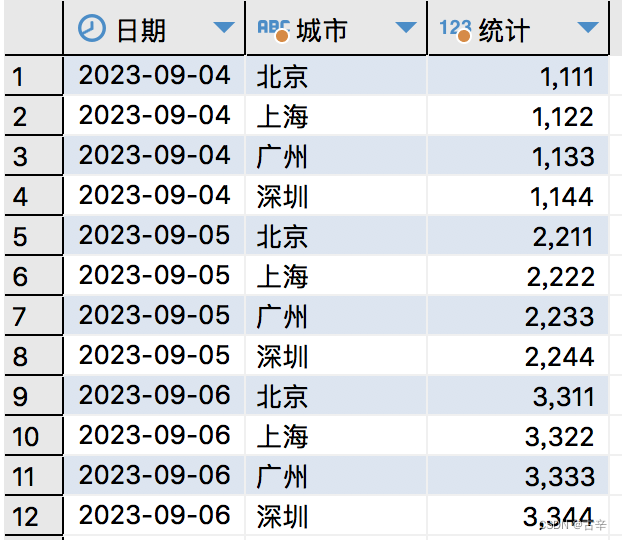
[PG]将一行数据打散成多行数据
原始数据 比如有如此表结构定义: 假如查询数据如下: select dt as "日期",bj_count as "北京", sh_count as "上海",gz_count as "广州", sz_count as "深圳" from city_stats order by dt--------------------…...

二蛋赠书一期:《快捷学习Spring》
文章目录 前言活动规则参与方式本期赠书《快捷学习Spring》关于本书作者介绍内容简介读者对象 结语 前言 大家好!我是二蛋,一个热爱技术、乐于分享的工程师。在过去的几年里,我一直通过各种渠道与大家分享技术知识和经验。我深知,…...
Threejs汽车展厅
2023-09-06-16-29-40 预览:https://9kt8fy-1234.csb.app/ 源码链接...
)
LeetCode:207. 课程表、210. 课程表 II(拓扑排序 C++)
目录 207. 课程表 题目描述: 实现代码与解析: 拓扑排序 210. 课程表 II 题目描述: 实现代码与解析: 拓扑排序 原理思路: 207. 课程表 题目描述: 你这个学期必须选修 numCourses 门课程࿰…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...
