2023高教社杯数学建模A题B题C题D题E题思路模型 国赛建模思路分享
文章目录
- 0 赛题思路
- 1 竞赛信息
- 2 竞赛时间
- 3 建模常见问题类型
- 3.1 分类问题
- 3.2 优化问题
- 3.3 预测问题
- 3.4 评价问题
- 4 建模资料
0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 竞赛信息
全国大学生数学建模竞赛(以下简称竞赛)是中国工业与应用数学学会主办的面向全国大学生 的群众性科技活动,旨在激励学生学习数学的积极性,提高学生建立数学模型和运用计算机技术解 决实际问题的综合能力,鼓励广大学生踊跃参加课外科技活动,开拓知识面,培养创造精神及合作 意识,推动大学数学教学体系、教学内容和方法的改革。
竞赛题目一般来源于科学与工程技术、人文与社会科学(含经济管理)等领域经过适当简化加工的实际问题,不要求参赛者预先掌握深入的专门知识,只需要学过高等学校的数学基础课程。题目有较大的灵活性供参赛者发挥其创造能力。参赛者应根据题目要求,完成一篇包括模型的假设、建立和求解、计算方法的设计和计算机实现、结果的分析和检验、模型的改进等方面的论文(即答卷)。竞赛评奖以假设的合理性、建模的创造性、结果的正确性和文字表述的清晰程度为主要标准。
竞赛分为本科组和专科组进行。本科学生只能参加本科组竞赛,不能参加专科组竞赛。专科(高职高专)学生一般参加专科组竞赛,也可参加本科组竞赛,无论参加何组竞赛,均必须在报名时确定,报名截止后不能再更改报名组别。同一参赛队的学生必须来自同一所学校。
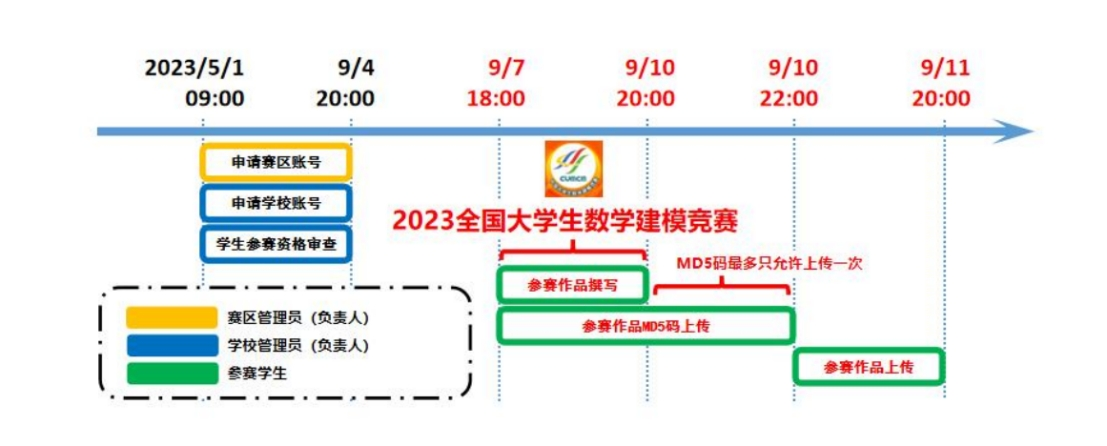
2 竞赛时间
报名结束时间:2023年9月4日20:00
比赛开始时间:2023年9月7日(周四)18:00
比赛结束时间:2023年9月10日(周日)20:00
3 建模常见问题类型
趁现在赛题还没更新,A君给大家汇总一下国赛数学建模经常使用到的数学模型,题目八九不离十基本属于一下四种问题,对应的解法A君也相应给出
分别为:
分类模型
优化模型
预测模型
评价模型
3.1 分类问题
判别分析:
又称“分辨法”,是在分类确定的条件下,根据某一研究对象的各种特征值判别其类型归属问题的一种多变量统计分析方法。
其基本原理是按照一定的判别准则,建立一个或多个判别函数;用研究对象的大量资料确定判别函数中的待定系数,并计算判别指标;据此即可确定某一样本属于何类。当得到一个新的样品数据,要确定该样品属于已知类型中哪一类,这类问题属于判别分析问题。
聚类分析:
聚类分析或聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集,这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。
聚类分析本身不是某一种特定的算法,而是一个大体上的需要解决的任务。它可以通过不同的算法来实现,这些算法在理解集群的构成以及如何有效地找到它们等方面有很大的不同。
神经网络分类:
BP 神经网络是一种神经网络学习算法。其由输入层、中间层、输出层组成的阶层型神经网络,中间层可扩展为多层。RBF(径向基)神经网络:径向基函数(RBF-Radial Basis Function)神经网络是具有单隐层的三层前馈网络。它模拟了人脑中局部调整、相互覆盖接收域的神经网络结构。感知器神经网络:是一个具有单层计算神经元的神经网络,网络的传递函数是线性阈值单元。主要用来模拟人脑的感知特征。线性神经网络:是比较简单的一种神经网络,由一个或者多个线性神经元构成。采用线性函数作为传递函数,所以输出可以是任意值。自组织神经网络:自组织神经网络包括自组织竞争网络、自组织特征映射网络、学习向量量化等网络结构形式。K近邻算法: K最近邻分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。
3.2 优化问题
线性规划:
研究线性约束条件下线性目标函数的极值问题的数学理论和方法。英文缩写LP。它是运筹学的一个重要分支,广泛应用于生产计划、物流运输、资源分配、金融投资等领域。建模方法:列出约束条件及目标函数;画出约束条件所表示的可行域;在可行域内求目标函数的最优解及最优值。
整数规划:
规划中的变量(全部或部分)限制为整数,称为整数规划。若在线性模型中,变量限制为整数,则称为整数线性规划。目前所流行的求解整数规划的方法往往只适用于整数线性规划。一类要求问题的解中的全部或一部分变量为整数的数学规划。从约束条件的构成又可细分为线性,二次和非线性的整数规划。
非线性规划:
非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。非线性规划研究一个 n元实函数在一组等式或不等式的约束条件下的极值问题,且 目标函数和约束条件至少有一个是未知量的非线性函数。目标函数和约束条件都是 线性函数的情形则属于线性规划。
动态规划:
包括背包问题、生产经营问题、资金管理问题、资源分配问题、最短路径问题和复杂系统可靠性问题等。
动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
多目标规划:
多目标规划是数学规划的一个分支。研究多于一个的目标函数在给定区域上的最优化。任何多目标规划问题,都由两个基本部分组成:
(1)两个以上的目标函数;
(2)若干个约束条件。有n个决策变量,k个目标函数, m个约束方程,则:
Z=F(X)是k维函数向量,Φ(X)是m维函数向量;G是m维常数向量;
3.3 预测问题
回归拟合预测
拟合预测是建立一个模型去逼近实际数据序列的过程,适用于发展性的体系。建立模型时,通常都要指定一个有明确意义的时间原点和时间单位。而且,当t趋向于无穷大时,模型应当仍然有意义。将拟合预测单独作为一类体系研究,其意义在于强调其唯“象”性。一个预测模型的建立,要尽可能符合实际体系,这是拟合的原则。拟合的程度可以用最小二乘方、最大拟然性、最小绝对偏差来衡量。
灰色预测
灰色预测是就灰色系统所做的预测。是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。其用等时距观测到的反映预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
马尔科夫预测:是一种可以用来进行组织的内部人力资源供给预测的方法.它的基本 思想是找出过去人事变动的 规律,以此来推测未来的人事变动趋势.转换矩阵实际上是转换概率矩阵,描述的是组织中员工流入,流出和内部流动的整体形式,可以作为预测内部劳动力供给的基础.
BP神经网络预测
BP网络(Back-ProPagation Network)又称反向传播神经网络, 通过样本数据的训练,不断修正网络权值和阈值使误差函数沿负梯度方向下降,逼近期望输出。它是一种应用较为广泛的神经网络模型,多用于函数逼近、模型识别分类、数据压缩和时间序列预测等。
支持向量机法
支持向量机(SVM)也称为支持向量网络[1],是使用分类与回归分析来分析数据的监督学习模型及其相关的学习算法。在给定一组训练样本后,每个训练样本被标记为属于两个类别中的一个或另一个。支持向量机(SVM)的训练算法会创建一个将新的样本分配给两个类别之一的模型,使其成为非概率二元线性分类器(尽管在概率分类设置中,存在像普拉托校正这样的方法使用支持向量机)。支持向量机模型将样本表示为在空间中的映射的点,这样具有单一类别的样本能尽可能明显的间隔分开出来。所有这样新的样本映射到同一空间,就可以基于它们落在间隔的哪一侧来预测属于哪一类别。
3.4 评价问题
层次分析法
是指将一个复杂的 多目标决策问题 作为一个系统,将目标分解为多个目标或准则,进而分解为多指标(或准则、约束)的若干层次,通过定性指标模糊量化方法算出层次单排序(权数)和总排序,以作为目标(多指标)、多方案优化决策的系统方法。
优劣解距离法
又称理想解法,是一种有效的多指标评价方法。这种方法通过构造评价问题的正理想解和负理想解,即各指标的最大值和最小值,通过计算每个方案到理想方案的相对贴近度,即靠近正理想解和远离负理想解的程度,来对方案进行排序,从而选出最优方案。
模糊综合评价法
是一种基于模糊数学的综合评标方法。 该综合评价法根据模糊数学的隶属度理论把定性评价转化为定量评价,即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。 它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
灰色关联分析法(灰色综合评价法)
对于两个系统之间的因素,其随时间或不同对象而变化的关联性大小的量度,称为关联度。在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
典型相关分析法:是对互协方差矩阵的一种理解,是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
主成分分析法(降维)
是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。在用统计分析方法研究多变量的课题时,变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。在很多情形,变量之间是有一定的相关关系的,当两个变量之间有一定相关关系时,可以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量,将重复的变量(关系紧密的变量)删去多余,建立尽可能少的新变量,使得这些新变量是两两不相关的,而且这些新变量在反映课题的信息方面尽可能保持原有的信息。设法将原来变量重新组合成一组新的互相无关的几个综合变量,同时根据实际需要从中可以取出几个较少的综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析,也是数学上用来降维的一种方法。
因子分析法(降维)
因子分析是指研究从变量群中提取共性因子的统计技术。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性,一科成绩好的学生,往往其他各科成绩也比较好,从而推想是否存在某些潜在的共性因子,或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子,可减少变量的数目,还可检验变量间关系的假设。
BP神经网络综合评价法
是一种按误差逆传播算法训练的多层前馈网络,是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层(input)、隐层(hide layer)和输出层(output layer)。
4 建模资料
资料分享: 最强建模资料


相关文章:

2023高教社杯数学建模A题B题C题D题E题思路模型 国赛建模思路分享
文章目录 0 赛题思路1 竞赛信息2 竞赛时间3 建模常见问题类型3.1 分类问题3.2 优化问题3.3 预测问题3.4 评价问题 4 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 竞赛信息 全国大学生数学建模…...
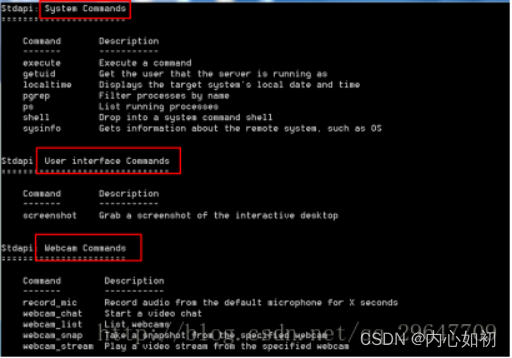
手机木马远程控制复现
目录 目录 前言 系列文章列表 渗透测试基础之永恒之蓝漏洞复现http://t.csdn.cn/EsMu2 思维导图 1,实验涉及复现环境 2,Android模拟器环境配置 2.1,首先从官网上下载雷电模拟器 2.2,安装雷电模拟器 2.3, 对模拟器网络进行配置 2.3.1,为什么要进行配置…...
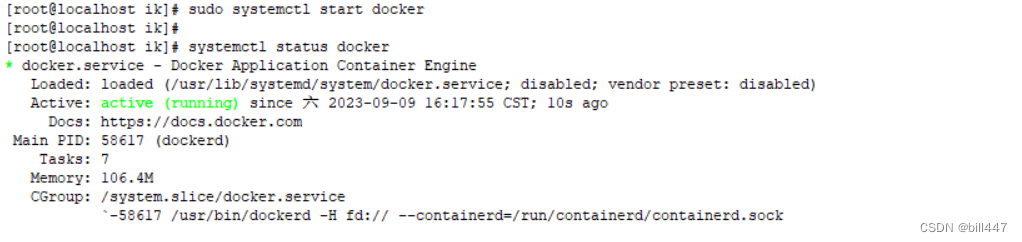
linux 安装Docker
# 1、yum 包更新到最新 yum update # 2、安装需要的软件包, yum-util 提供yum-config-manager功能,另外两个是devicemapper驱动依赖的 yum install -y yum-utils device-mapper-persistent-data lvm2 # 3、 设置yum源 yum-config-manager --add-repo h…...

Java中的值传递与引用传递 含面试题
面试题分享 点我直达 2023最新面试合集链接 2023大厂面试题PDF 面试题PDF版本 java、python面试题 项目实战:AI文本 OCR识别最佳实践 AI Gamma一键生成PPT工具直达链接 玩转cloud Studio 在线编码神器 玩转 GPU AI绘画、AI讲话、翻译,GPU点亮AI想象空间 史上最全文档…...
函数用法详解)
SQL中CONVERT()函数用法详解
SQL中CONVERT函数格式: CONVERT(data_type,expression[,style]) 参数说明: expression 是任何有效的 Microsoft SQL Server™ 表达式。。 data_type 目标系统所提供的数据类型,包括 bigint 和 sql_variant。不能使用用户定义的数据类型。 length nchar、nva…...
借助各大模型的优点生成原创视频(真人人声)Plus
【技术背景】 众所周知,组成视频的3大元素,即文本语音图片。接着小编逐一介绍生成原创视频的过程。 【文本生成】 天工AI搜索(thttp://iangong.cn) 直接手机短信验证就可以使用,该大模型已经接入互联网,…...

技能大赛物联网赛项参赛软件建设方案
一、概述 信息与通信技术的目标已经从任何时间、任何地点连接任何人,发展到连接任何物品的阶段,而万物的连接就形成了物联网。物联网的主要特征是通过条码识读设备、射频识别 (RFID)装置、红外感应器、全球定位系统、激光扫描器等信息传感设备…...
)
蓝桥杯官网练习题(凯撒加密)
题目描述 给定一个单词,请使用凯撒密码将这个单词加密。 凯撒密码是一种替换加密的技术,单词中的所有字母都在字母表上向后偏移 3 位后被替换成密文。即 a 变为 d,b 变为 e,⋯⋯,w 变为z,x 变为 a&#x…...

JavaScript 数组中常用的方法
添加 push:数组末尾添加unshift:数组首位添加splice(1, 0, ‘新增内容’):再指定位置插入,第二参数为0,表示新增;大于0,表示修改 删除 pop:删除末尾shift:删除首位slice(…...

YOLOV7改进-添加基于注意力机制的目标检测头(DYHEAD)
DYHEAD 复制到这: 1、models下新建文件 2、yolo.py中import一下 3、改IDetect这里 4、论文中说6的效果最好,但参数量不少,做一下工作量 5、在进入IDetect之前,会对RepConv做卷积 5、因为DYHEAD需要三个层输入的特征层一致&am…...

爬虫爬取mp3文件例子
相信训练模型时数据集的获取也是一个很头疼的事情,搞cv领域的可以扛着摄像头架起三脚架拍摄获取(以前干过),但是如果是nlp领域的呢,特别是chatgpt等大模型出来后对这类文本等数据的需求更大,如果没有现成的…...

说说什么是间隙锁
分析&回答 间隙锁为了解决RR(可重复读)级别下当前读导致的幻读问题,锁的对象是索引叶子节点的next指针。 快照读 在RR隔离级别下:快照读有可能读到数据的历史版本,也有可能读到数据的当前版本。所以快照读无需用…...
)
python小题库(三)
大家好呀,今天继续更新python小题库。 题11:实现学生成绩排序 # 问题:实现学生成绩排序 # 如学生的成绩是字典形式 students [{"sno": 101, "sname": "小张", "sgrade": 88},{"sno": 10…...

【前端设计模式】之单例模式
在前端开发中,单例模式是一种常见的设计模式,用于确保一个类只有一个实例,并提供全局访问点。在实现单例模式时,有一些最佳实践和高级技巧可以帮助我们编写更优雅和可维护的代码。 1. 使用闭包 使用闭包是实现单例模式的一种常见…...
常用指令(一))
Linux——(第六章)常用指令(一)
目录 一、帮助指令 1.man获取帮助信息 2.help指令 3.常用快捷键 二、文件和目录相关指令 1.pwd 指令 2.ls 指令 3.cd 指令 4.mkdir 指令 5.rmdir指令 6.touch指令 7.cp 指令 8.rm 指令 9.mv 指令 10.cat 指令 11.more 指令 12.less 指令 13.echo 指令 14.he…...

第19章_瑞萨MCU零基础入门系列教程之RTC
本教程基于韦东山百问网出的 DShanMCU-RA6M5开发板 进行编写,需要的同学可以在这里获取: https://item.taobao.com/item.htm?id728461040949 配套资料获取:https://renesas-docs.100ask.net 瑞萨MCU零基础入门系列教程汇总: ht…...
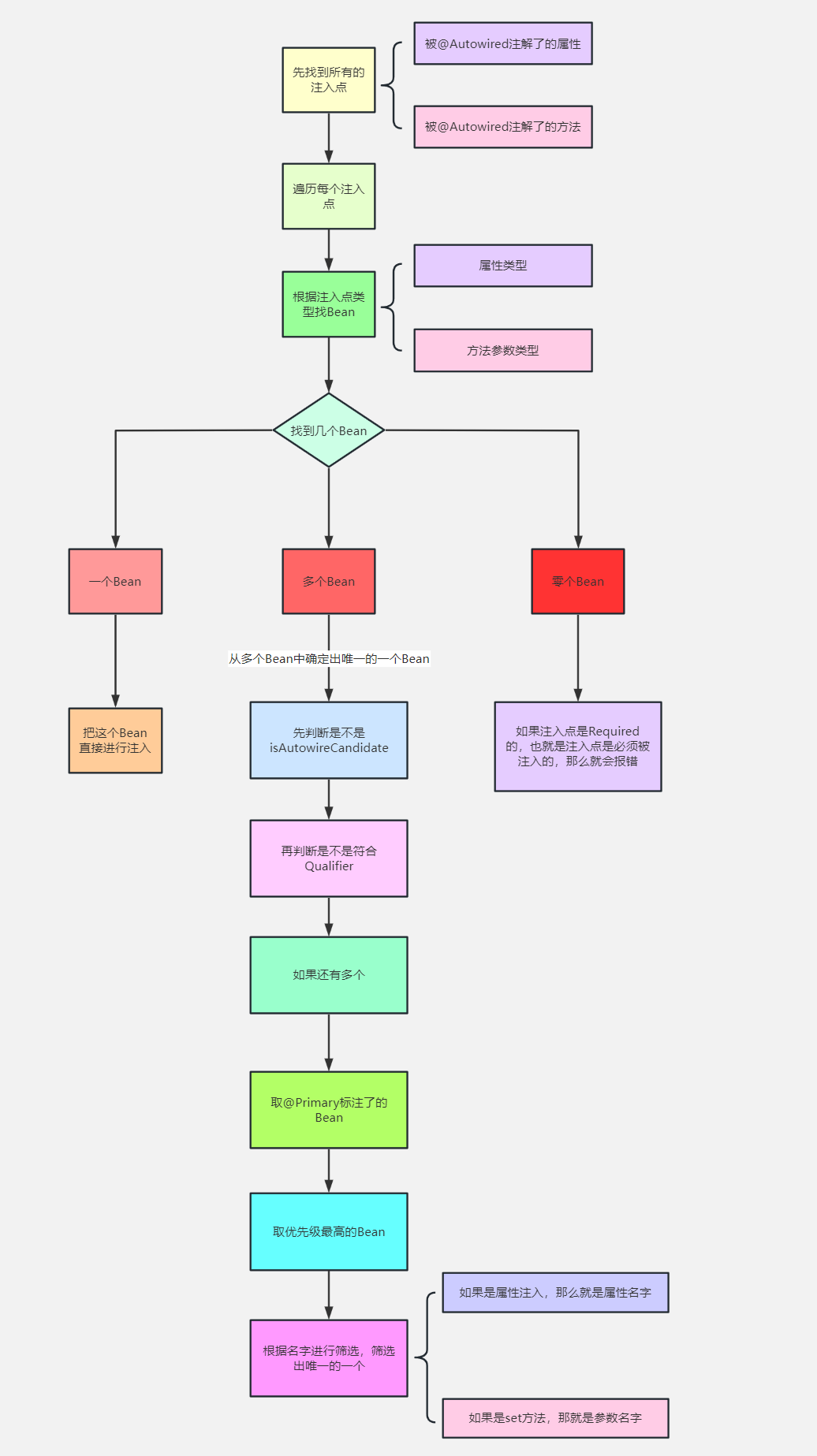
6、Spring之依赖注入源码解析(上)
依赖注入底层原理流程图: Spring中Bean的依赖注入原理| ProcessOn免费在线作图,在线流程图,在线思维导图 Spring中到底有几种依赖注入的方式? 首先分两种: 手动注入自动注入手动注入 在XML中定义Bean时,就是手动注入,因为是程序员手动给某个属性指定了值。 <bean n…...

vscode各种配置的方法
一. vscode配置 vscode 是微软公司提供的一个 代码编辑器。是做C/C常用的编辑器。 在安装后,可以根据自己需要自行安装常用的配置插件。同时,也可以在设置栏设置自己需要的功能,以方便使用。 下面学习 vscode的几种常见的设置。 二. vsco…...
)
每天几道面试题(第一天)
目录 第一幕 、第一场)某大厦楼下大门前第二场)电梯中第三场)走廊中 友情提醒 背面试题很枯燥,加入一些戏剧场景故事人物来加深记忆。PS:点击文章目录可直接跳转到文章指定位置。 第一幕 、 第一场)某大厦楼下大门前…...

[paddle]paddlepaddle官方安装命令合集
官方最新安装命令: https://www.paddlepaddle.org.cn/install/quick?docurl/documentation/docs/zh/install/pip/windows-pip.html 历史命令: V2.4 环境支持 Python 版本 3.6/3.7/3.8/3.9/3.10 PIP安装方式 Windows 安装 GPU版本支持CUDA 10.2/11.…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Redis专题-实战篇一-基于Session和Redis实现登录业务
GitHub项目地址:https://github.com/whltaoin/redisLearningProject_hm-dianping 基于Session实现登录业务功能提交版本码:e34399f 基于Redis实现登录业务提交版本码:60bf740 一、导入黑马点评后端项目 项目架构图 1. 前期阶段2. 后续阶段导…...

NLP常用工具包
✨做一次按NLP项目常见工具的使用拆解 1. tokenizer from torchtext.data.utils import get_tokenizertokenizer get_tokenizer(basic_english) text_sample "Were going on an adventure! The weather is really nice today." tokens tokenizer(text_sample) p…...

Java + Spring Boot + Mybatis 插入数据后,获取自增 id 的方法
在 MyBatis 中使用 useGeneratedKeys"true" 获取新插入记录的自增 ID 值,可通过以下步骤实现: 1. 配置 Mapper XML 在插入语句的 <insert> 标签中设置: xml 复制 下载 运行 <insert id"insertUser" para…...
