【C++杂货铺】探索stack和queue的底层实现

文章目录
- 一、stack的介绍和使用
- 1.1 stack的介绍
- 1.2 stack的使用
- 1.2.1 最小栈
- 1.2.2 栈的压入、弹出序列
- 1.2.3 逆波兰表达式求值
- 1.2.4 用栈实现队列
- 二、queue的介绍和使用
- 2.1 queue的介绍
- 2.2 queue的使用
- 2.2.1 二叉树的层序遍历
- 三、模拟实现
- 3.1 stack模拟实现
- 3.2 queue模拟实现
- 四、容器适配器
- 4.1 什么是适配器?
- 4.2 STL标准库中stack和queue的底层结构
- 4.3 deque的简单介绍
- 4.3.1 deque的原理介绍
- 4.3.2 deque的缺陷
- 4.4 为什么选择deque作为stack和queue的底层默认容器?
- 五、结语
一、stack的介绍和使用
1.1 stack的介绍
-
stack 是一种容器适配器,专门用在具有后进先出的上下文环境中。只能从容器的一端进行元素的插入与提取操作。
-
stack 是作为容器适配器被实现的,容器适配器即是对特定类封装作为其底层的容器,并提供一组特定的成员函数来访问其元素,使得元素在特定容器的尾部(栈顶)被压入和弹出。
-
stack 的底层容器可以使任何标准的容器类模板或者一些其它特定的容器类,这些容器类应该支持以下操作:
-
empty:判空操作
-
back:获取尾部元素操作
-
push_back:尾部插入元素操作
-
pop_back:尾部删除元素操作
-
-
标准容器 vector、deque、list 均符合这些需求,默认情况下,如果没有为 stack 指定特定的底层容器,默认情况下使用 deque。

1.2 stack的使用
| 函数说明 | 接口说明 |
|---|---|
| stack() | 构造空的栈 |
| empty() | 检测栈 stack 是否为空 |
| size() | 返回 stack 中元素的个数 |
| top() | 返回栈顶元素的引用 |
| push() | 将元素 val 压入 stack 中 |
| pop() | 将 stack 中尾部的元素弹出 |
1.2.1 最小栈

本题的思路是用两个栈来实现,其中一个栈 _st 用来正常存储数据,另一个栈 _minst 用来存储最小的数据。具体实现就是在往 _st 中插入数据的时候进行判断,如果当前插入的数据 val 小于等于 _minst 栈顶的数据,那就将 val 也插入到 _minst 这个栈中。否则直将数据插入 _st 中。在 pop 数据的时候,先取 _st 的栈顶元素和 _minst 的栈顶元素进行比较,如果二者相等,那就同时 pop _st 和 _minst 的栈顶元素,否则就值 pop _st 的栈顶元素。要获取堆栈中的最小元素直接返回 _minst 的栈顶元素即可。
class MinStack
{
public:MinStack() {}void push(int val) {_st.push(val);if(_minst.empty() || val <= _minst.top()){_minst.push(val);}}void pop() {if(_st.top() == _minst.top()){_minst.pop();}_st.pop();}int top() {return _st.top();}int getMin() {return _minst.top();}
private:stack<int> _st;stack<int> _minst;
};
1.2.2 栈的压入、弹出序列

本题的解题思路是用一个栈来模拟。即先定义一个栈 st 然后给栈中入一个数据,接着取栈顶的数据和出栈序列 popV 当前位置元素进行比较进行比较,如果不相等则继续从入栈序列 pushV 中拿数据往栈 st 中入,如果相等就出栈。这里需要注意,有可能需要连续多次出栈。直到最终将入栈序列 pushV 中的数据全入栈,最后判断栈 st 是否为空,如果为空,就说明该出栈序列正确。如果不空就说明该出栈序列有问题。
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {// write code herestack<int> st;size_t push_pos = 0, pop_pos = 0;while(push_pos < pushV.size()){//先入一个元素st.push(pushV[push_pos++]);if(st.top() != popV[pop_pos]){//不匹配继续入数据continue;}while(!st.empty() && st.top() == popV[pop_pos]){//匹配,出数据st.pop();pop_pos++;}}return st.empty();}
};
代码优化:我们可以发现上面代码中不匹配逻辑里面其实啥也没干,因此我们可以把这段代码给删掉,上面加上是为了使逻辑更加清晰。
class Solution {
public:/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param pushV int整型vector * @param popV int整型vector * @return bool布尔型*/bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {// write code herestack<int> st;size_t push_pos = 0, pop_pos = 0;while(push_pos < pushV.size()){//先入一个元素st.push(pushV[push_pos++]);while(!st.empty() && st.top() == popV[pop_pos]){//匹配,出数据st.pop();pop_pos++;}}return st.empty();}
};
1.2.3 逆波兰表达式求值

逆波兰表达式也被叫做后缀表达式。什么是后缀表达式呢?先来了解一下中缀表达式,中缀表达式就是我们平时最常见的,例如: 2 + 3 ∗ 1 2+3*1 2+3∗1,就是一个典型的中缀表达式。将前面的中缀表达式变成后缀表达式得到:2 1 3 * +,这就是一个后缀表达式,后缀表达式相较于中中缀表达式,操作数顺序不变,操作符按优先级重排。这道题目就是要求我们对后缀表达式进行求解。求解后缀表达式,我们可以借助一个栈,遇到操作数入栈,遇到操作符从栈中出两个元素进行运算,将运算结果继续入栈。最终栈顶的元素就是整个逆波兰表达式的结果。
class Solution {
public:int evalRPN(vector<string>& tokens) {stack<int> st;size_t pos = 0;while(pos < tokens.size()){if(tokens[pos] != "+" && tokens[pos] != "-" && tokens[pos] != "*" && tokens[pos] != "/"){//如果是数字就入栈int num = stoi(tokens[pos]);st.push(num);}else{//不是数字就从栈中取两个元素出来int val1 = st.top();st.pop();int val2 = st.top();st.pop();int ret = 0;if(tokens[pos] == "+"){ret = val2 + val1;}else if(tokens[pos] == "-"){ret = val2 - val1;}else if(tokens[pos] == "*"){ret = val2 * val1;}else if(tokens[pos] == "/"){ret = val2 / val1;}//将计算结果继续入栈st.push(ret);}pos++;}return st.top();}
};
注意:在写上面这段代码的时候有下面几点需要特别注意,首先这是一个 string 数组,会涉及到 string 转 int 。其次需要注意在从栈中取数的时候,第一次取出的是右操作数,第二次取出的是左操作数,因此 val2 应该做左操作数,val1 应该做右操作数,尤其是减法运算和除法运算,这两个操作数的顺序必须得到保证。
补充:这里补充一个小知识点:如何将中缀表达式转换成后缀表达式。主要过程分为以下几步:
-
遇到操作数就输出(这里的输出是将其存储到某种容器里)。
-
遇到操作符,根据优先级的顺序分为以下两种情况:
-
栈为空或当前操作符比栈顶的优先级高,继续入栈。
-
栈不为空且当前操作符比栈顶的优先级低或者相等,则输出栈顶操作符,继续执行第二步。
-
-
中缀表达式结束后,依次出栈里面的操作符。
小Tips:当前操作符能否计算取决于后一个操作符的优先级是否高于自己,所以每当我们遇到一个操作符的时候,先不着急将它入栈,先和栈顶的操作符进行优先级比较,如果当前操作符的优先级比栈顶操作符的优先级低或者相等,我们就可以取出栈顶这个操作符进行运算。如果遇到括号可以走一个递归。其次就是需要想办法确定符号的优先级。
1.2.4 用栈实现队列

将一个栈当做输入栈,用于压入 push 传入的数据,另一个栈当做输出栈,用于 pop 和 peek 操作。每次 pop 或 peek 时,若输出栈为空则将输入栈的全部数据依次弹并压入输出栈,这样输出栈从栈顶往栈底的顺序就是队列从队首往队尾的顺序。
class MyQueue {
public:MyQueue() {}void push(int x) {input_st.push(x);}int pop() {if(output_st.empty()){while(!input_st.empty()){output_st.push(input_st.top());input_st.pop();} }int ret = output_st.top();output_st.pop();return ret;}int peek() {if(output_st.empty()){while(!input_st.empty()){output_st.push(input_st.top());input_st.pop();}}return output_st.top();}bool empty() {return input_st.empty() && output_st.empty();}
private:stack<int> input_st;stack<int> output_st;
};
二、queue的介绍和使用
2.1 queue的介绍
-
队列是一种容器适配器,专门用于在FIFO上下文中执行先进先出操作,其中从容器的一端插入元素,另一端提取元素。
-
队列作为容器适配器实现,容器适配器即将特定的容器类封装最为其底层容器,queue 提供一组特定的成员函数来访问其元素。元素从队尾入队列,从对头出队列。
-
底层容器可以是标准容器模板之一,也可以是其他专门设计的容器类。该底层容器应至少支持以下操作:
-
empty:检查队列是否为空
-
size:返回队列中有效元素的个数
-
front:返回对头元素的引用
-
back:返回队尾元素的引用
-
push_back:在队列尾部入队列
-
pop_front:在队列头部出队列
-
-
标准容器类 deque 和 list 满足了这些要求。默认情况下,如果没有为 queue 实例化指定容器类,则使用标准容器 deque。

2.2 queue的使用
| 函数声明 | 接口说明 |
|---|---|
| queue() | 构造空队列 |
| empty() | 检测队列是否为空,是返回 true,否则返回 false |
| size() | 返回队列中有效元素个数 |
| front() | 返回队头元素的引用 |
| back() | 返回队尾元素的引用 |
| push() | 在队尾将元素 val 入队列 |
| pop() | 将队头元素出队列 |
2.2.1 二叉树的层序遍历

二叉树的层序遍历可以借助队列来实现,从根节点开始,先让父节点入队列,在出队尾节点的同时,将该节点的左孩子和右孩子依次入队列。直到队列为空,从队列中出出来的结果就是层序遍历的结果。这道题目需要将同一层的所有节点都存入一个一维数组,再将这些一维数组组合成一个二维数组返回。我们前面的这种做法会导致队列中出现两层节点混在意的情况,因此我们可以定义一个变量 levelSize 来记录每一层的节点数。具体代码如下:
class Solution
{
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> retV;queue<TreeNode*> qu;int levelSize = 0;qu.push(root);while(!qu.empty()){vector<int> tmp;levelSize = qu.size();while(levelSize != 0){TreeNode* top = qu.front();if(top != nullptr){tmp.push_back(top->val);qu.push(top->left);qu.push(top->right);} qu.pop();levelSize--;}if(!tmp.empty()){retV.push_back(tmp);}}return retV;}
};
三、模拟实现
3.1 stack模拟实现
template<class T, class Continer = vector<T>>class stack{public:stack(){}void push(const T& val){_con.push_back(val);}void pop(){_con.pop_back();}T& top(){return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}private:Continer _con;};
小Tips:stack 可以使用 vector 或者 list 来实现,效率相当。插入数据就相当于尾插,删除栈顶元素就相当于尾删。
3.2 queue模拟实现
template<class T, class Continer = std::list<T>>
class queue
{
public:queue(){}void push(const T& val){_con.push_back(val);}void pop(){_con.pop_front();//这里不再支持vector}T& front(){return _con.front();}T& back(){return _con.back();}size_t size(){return _con.size();}bool empty(){return _con.empty();}
private:Continer _con;
};
小Tips:栈不能借助 vector 来实现,因为出队列,相当于删除 vector 中的第一个元素,而对 vector 头删会涉及挪动数据,效率相较于 list 会有所下降。
四、容器适配器
4.1 什么是适配器?
适配器是一种设计模式(设计模式是一套被反复使用的、多数人知晓的、经过分类编目的、代码设计经验的总结),该种模式是将一个类的接口转换成客户希望的另外一个接口。

4.2 STL标准库中stack和queue的底层结构
虽然 stack 和 queue 中也可以存放元素,但在 STL 中并没有将其划分在容器行列,而是将其称为容器适配器,这是因为 stack 和 queue 只是对其他容器的接口进行了包装,STL 中 stack 和 queue 默认使用 deque。
4.3 deque的简单介绍
4.3.1 deque的原理介绍
deque(双端队列):是一种双开口的“连续”空间的数据结构,双开口的含义是:可以在头尾两端进行插入和删除操作,且时间复杂度为O(1),与 vector 比较,头插效率高,不需要搬移元素;与 list 比较,空间利用率比较高。

deque并不是真正连续的空间,而是由一段段连续的小空间拼接而成的,实际 deque 类似于一个动态的二维数组,其底层结构如下图所示:

双端队列底层是一段假象的连续空间,实际是分段连续的,为了维护其“整体连续”以及随机访问的假象,落在了 deque 的迭代器身上,因此 deque 的迭代器设计的就比较复杂,如下图所示:


4.3.2 deque的缺陷
-
与 vector 比较,deque 的优势是:头部插入和删除时,不需要搬移元素,效率特别高,而且在扩容时,也不需要搬移大量的元素,因此其效率是比 vector 高的。
-
与 list 比较,其底层空间是连续的,空间利用率比较高,不需要存储额外字段。
-
但是,deque 有一个致命缺陷:不适合遍历,因为在遍历时,deque 的迭代器要频繁的去检测其是否移动到某段小空间的边界,导致效率低下,而序列式场景中,可能需要经常遍历,因此在实际中,需要线性结构式,大多数情况下优先考虑 vector 和 list,deque 的应用并不多,而目前能看到的一个应用场景就是,STL 用其作为 stack 和 queue 的底层数据结构。
4.4 为什么选择deque作为stack和queue的底层默认容器?
stack 是一种后进先出的特殊线性数据结构,因此只要是具有 push_back() 和 pop_back() 操作的线性结构,都可以作为 stack 的底层容器,比如 vector 和 list 都可以;queue 是先进先出的特殊线性数据结构,只要具有 push_back() 和 pop_front() 操作的线性结构,都可以作为 queue de 底层容器,比如 list。但是 STL 中对 stack 和 queue 默认选择 deque 作为其底层容器,主要是因为:
-
stack 和 queue 不需要遍历(因此 stack 和 queue 没有迭代器),只需要在固定的一端或者两端进行操作。
-
在 stack 中元素增长时,deque 比 vector 的效率高(扩容时不需要搬移大量数据);queue 中的元素增长时,deque 不仅效率高,而且内存利用率高。
五、结语
今天的分享到这里就结束啦!如果觉得文章还不错的话,可以三连支持一下,春人的主页还有很多有趣的文章,欢迎小伙伴们前去点评,您的支持就是春人前进的动力!

相关文章:

【C++杂货铺】探索stack和queue的底层实现
文章目录 一、stack的介绍和使用1.1 stack的介绍1.2 stack的使用1.2.1 最小栈1.2.2 栈的压入、弹出序列1.2.3 逆波兰表达式求值1.2.4 用栈实现队列 二、queue的介绍和使用2.1 queue的介绍2.2 queue的使用2.2.1 二叉树的层序遍历 三、模拟实现3.1 stack模拟实现3.2 queue模拟实现…...

“系统的UI”——SystemUI
SystemUI的实现 以StatusBar为例,来分析下Android系统具体是如何实现它们的。 相关代码分为两部分,即: Service部分 代码路径:frameworks/base/services/java/com/android/server。 应用部分 代码路径:frameworks…...
类和对象:构造函数,析构函数与拷贝构造函数
1.类的6个默认成员函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,编译器…...

谈谈Java的特点和优点以及选择Java的原因
 如果面试官问你:请你说说Java的特点和优点,为什么要选择Java?你该怎么回答? 得分点 Java的特点 Java与C的区别 Java的优点标准回答 Java是一门非常纯粹的面向对象的编程语言,它吸收了C语言的各种优…...
面试)
消息队列(MQ)面试
目录 讲一讲MQ 面试官: 在你之前的项目中,你是否使用过消息队列(MQ)?能详细介绍一下你在项目中如何使用MQ吗? 在用户和用户之间的多对多聊天通信中如何使用,请具体来讲一下。 那你可以讲一下消息的确认…...

无涯教程-JavaScript - COUPNUM函数
描述 COUPNUM函数返回结算日和到期日之间应付的息票数量,四舍五入到最接近的整数。 语法 COUPNUM (settlement, maturity, frequency, [basis])争论 Argument描述Required/OptionalSettlement 证券的结算日期。 证券结算日期是指在发行日期之后将证券交易给买方的日期。 Re…...

上海控安携汽车网络安全新研产品出席AUTOSEMO“恒以致远,共创共赢”主题研讨会
8月31日,AUTOSEMO“恒以致远,共创共赢”主题研讨会在天津成功召开。本次大会由中国汽车工业协会软件分会中国汽车基础软件生态标委会(简称:AUTOSEMO)与天津市西青区人民政府联合主办。现场汇聚了100余位来自产学研政企…...

小程序引入高德/百度地图坐标系详解
小程序引入高德/百度地图坐标系详解 官网最近更新时间:最后更新时间: 2021年08月17日 高德官网之在原生小程序中使用的常见问题 链接 目前在小程序中使用 高德地图只支持以下功能 :地址描述、POI和实时天气数据 小结:从高德api中获取数…...
英诺森 “供应链智能数据平台”荣获“科技进步奖”
近日,2023年中国物流与采购联合会科学技术奖正式公布,该奖项经国家科技部批准,在国家科学技术奖励工作办公室登记备案,是我国物流行业最具影响力的奖项之一。 英诺森联合客户申报的科技项目“英诺森供应链智能数据平台”…...

kafka 3.5 主题分区的Follower创建Fetcher线程从Leader拉取数据源码
Kakfa集群有主题,每一个主题下又有很多分区,为了保证防止丢失数据,在分区下分Leader副本和Follower副本,而kafka的某个分区的Leader和Follower数据如何同步呢?下面就是讲解的这个 首先要知道,Follower的数据…...

Golang web 项目中实现自定义 recovery 中间件
为什么需要实现自定义 recovery 中间件? 在 Golang 的 Web 项目中,自定义 recovery 中间件是一种常见的做法,用于捕获并处理应用程序的运行时错误,以避免整个应用程序崩溃并返回对应格式的响应数据。 很多三方 web 框架…...
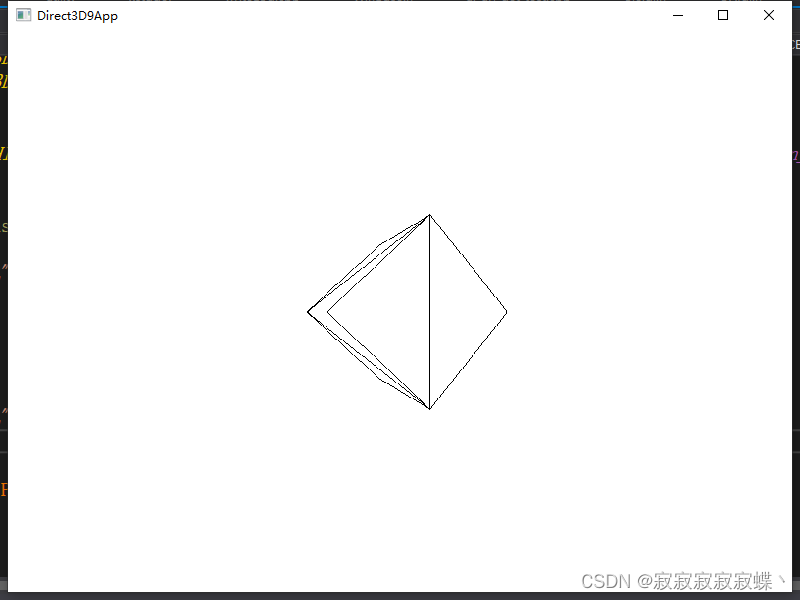
Direct3D绘制旋转立方体例程
初始化文件见Direct3D的初始化_direct3dcreate9_寂寂寂寂寂蝶丶的博客-CSDN博客 D3DPractice.cpp #include <windows.h> #include "d3dUtility.h" #include <d3dx9math.h>IDirect3DDevice9* Device NULL; IDirect3DVertexBuffer9* VB NULL; IDirect3…...

ElementUI浅尝辄止31:Tabs 标签页
选项卡组件:分隔内容上有关联但属于不同类别的数据集合。 常见于网站内容信息分类或app内容信息tab分类 1.如何使用? Tabs 组件提供了选项卡功能,默认选中第一个标签页,你也可以通过 value 属性来指定当前选中的标签页。 <temp…...

将 ChatGPT 用于数据科学项目的指南
推荐:使用 NSDT场景编辑器 快速搭建3D应用场景 我们都知道 ChatGPT 的受欢迎程度以及人们如何使用它来提高生产力。但是,如果您是新手,则值得注册ChatGPT免费演示并尝试它所能做的一切。您还应该参加我们的 ChatGPT 简介课程,学习…...

06-JVM对象内存回收机制深度剖析
上一篇:05-JVM内存分配机制深度剖析 堆中几乎放着所有的对象实例,对堆垃圾回收前的第一步就是要判断哪些对象已经死亡(即不能再被任何途径使用的对象)。 1.引用计数法 给对象中添加一个引用计数器,每当有一个地方引…...

[VSCode] 替换掉/去掉空行
VSCode中使用快捷键CtrlH,出现替换功能,在上面的“查找”框中输入正则表达式: ^\s*(?\r?$)\n然后选择右侧的“使用正则表达式”;“替换”框内为空,点击右侧的“全部替换”,即可去除所有空行。 参考 [VS…...
时序分解 | MATLAB实现ICEEMDAN+SE改进的自适应经验模态分解+样本熵重构分量
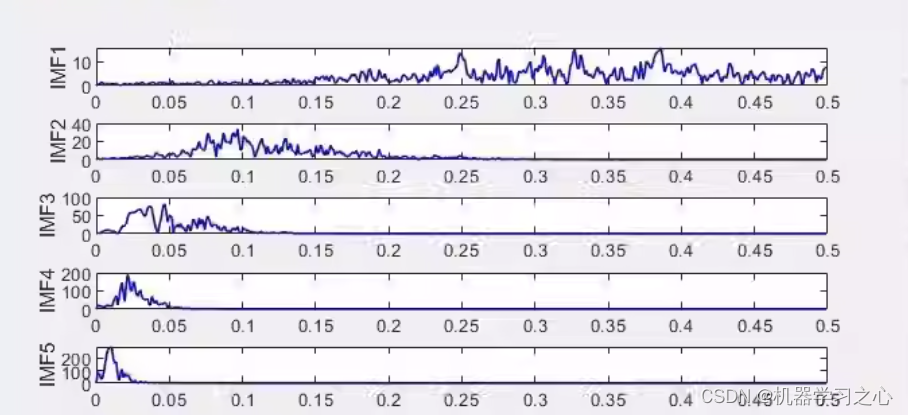
时序分解 | MATLAB实现ICEEMDANSE改进的自适应经验模态分解样本熵重构分量 目录 时序分解 | MATLAB实现ICEEMDANSE改进的自适应经验模态分解样本熵重构分量效果一览基本介绍程序设计参考资料 效果一览 基本介绍 ICEEMDANSE改进的自适应经验模态分解样本熵重构分量 包括频谱图 避…...

python内网环境安装第三方包【内网搭建开发环境】
文章目录 一、问题二、解决方法三、代码实现一、问题 内网安装第三方包的应用场景,一般是一些需要在没网的环境下进行开发的情况。这些环境一般仅支持本地局域网访问,所以只能在不下载任何第三方包的情况下艰难开发。 二、解决方法 将当前应用依赖的第三方包提前下载到本地…...

7.13 在SpringBoot中 正确使用Validation实现参数效验
文章目录 前言引入Maven依赖一、POST/PUT RequestBody参数校验1.1 Valid或Validated注解配合constraints注解1.2 测试运行 二、GET/DELETE RequestParam参数校验2.1 Validated注解配合constraints注解2.2 测试运行 三、GET 无注解参数校验3.1 Valid或Validated注解配合constrai…...

Matlab图像处理之Lee滤波器
目录 一、前言:二、LEE滤波器2.1 LEE滤波器原理2.2 LEE滤波器实现步骤三、MATLAB代码示例一、前言: LEE滤波器是一种常用于合成孔径雷达(SAR)图像去噪的滤波器。它能增强图像的局部对比度。今天我们将通过MATLAB来实现这种滤波器。 二、LEE滤波器 2.1 LEE滤波器原理 LEE滤…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...
