代码随想录训练营第五十六天| 583. 两个字符串的删除操作 、72. 编辑距离
583. 两个字符串的删除操作
题目链接/文章讲解/视频讲解:代码随想录
1.代码展示
//583.两个字符串的删除操作
int minDistance(string word1, string word2) {//step1 构建dp数组,dp[i][j]的含义是要使以i-1为结尾的word1和以j-1为结尾的word2//删除其元素后相同所需最小的删除步数vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));//step2 状态转移方程//if (word1[i - 1] == word[j - 1]) 此时不需要删除,dp[i][j] = dp[i - 1][j - 1];//else ,dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2);//对应着三种情况,删除word1[i - 1]或者word2[j - 1]或者同时删除//step3 初始化for (int i = 0; i <= word1.size(); i++) {dp[i][0] = i;}for (int j = 0; j <= word2.size(); j++) {dp[0][j] = j;}//step4 开始遍历for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min({ dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 2 });}}}return dp[word1.size()][word2.size()];
}2.本题小节
思考: 首先明确dp[i][j]的含义是下标以i-1为结尾的word1和以下标为j-1结尾的word2删除元素相等所需的最少步骤。当word1[i - 1] == word2[j - 1]时,此时不需要删除元素,因此dp[i][j] = dp[i - 1][j - 1];当不相等时,此时既可以删除word1下标i-1处的元素,对应的是dp[i - 1][j] + 1,也可以删除word2下标j-1处的元素,对应的是dp[i][j-1] + 1,也可以是同时删除掉,对应的是dp[i - 1][j - 1] + 2,因此dp[i][j]从上面三种情况中选择最小的。初始化时要注意,dp[i][0]对应的位置初始化为i,dp[0][j]对应位置初始化为j,这个很好想。
步骤:注意思考的内容,按照步骤来即可。
72. 编辑距离
题目链接/文章讲解/视频讲解:代码随想录
1.代码展示
//72.编辑距离
int minDistance(string word1, string word2) {//step1 构建dp数组,dp[i][j]的含义是要使以i-1为结尾的word1和以j-1为结尾的word2//相同需要操作(增加、删减、替换)的次数vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));//step2 状态转移方程//if (word1[i - 1] == word[j - 1]) 此时不需要处理,dp[i][j] = dp[i - 1][j - 1];//else ,dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1);//对应着三种情况,删掉word1[i - 1](删除),删掉word2[j - 1](增加),替换//step3 初始化for (int i = 0; i <= word1.size(); i++) {dp[i][0] = i;}for (int j = 0; j <= word2.size(); j++) {dp[0][j] = j;}//step4 开始遍历for (int i = 1; i <= word1.size(); i++) {for (int j = 1; j <= word2.size(); j++) {if (word1[i - 1] == word2[j - 1]) {dp[i][j] = dp[i - 1][j - 1];}else {dp[i][j] = min({ dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1 });}}}return dp[word1.size()][word2.size()];
}2.本题小节
思考:dp[i][j]的含义是以下标i-1为结尾的word1通过增加,删除,替换能够变成以下标j-1为结尾的word2所需要的最小步骤。当word1[i - 1] == word2[j - 1]时,此时不需要操作,则dp[i][j] = dp[i - 1][j - 1];当不相等时,可以通过删除(删除word1[i - 1])、增加(删除word2[j - 1])、和替换(word1[i - 1]替换为word[j - 1])来操作,分别对应的时dp[i - 1][j] + 1、dp[i][j - 1] + 1、dp[i - 1][j - 1] + 1,选择最小情况,初始化和上题一样。
基本步骤:根据思考和动态规划的步骤来即可。
编辑距离总结:代码随想录
相关文章:

代码随想录训练营第五十六天| 583. 两个字符串的删除操作 、72. 编辑距离
583. 两个字符串的删除操作 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //583.两个字符串的删除操作 int minDistance(string word1, string word2) {//step1 构建dp数组,dp[i][j]的含义是要使以i-1为结尾的word1和以j-1为结尾的word2//删除其元…...

hive解决了什么问题
hive出现的原因 Hive 出现的原因主要有以下几个: 传统数据仓库无法处理大规模数据:传统的数据仓库通常采用关系型数据库作为底层存储,这种数据库在处理大规模数据时效率较低。MapReduce 难以使用:MapReduce 是一种分布式计算框架…...

Lumion 和 Enscape 应该选择怎样的笔记本电脑?
Lumion 和 Enscape实时渲染对配置要求高,本地配置不够,如何快速解决: 本地普通电脑可一键申请高性能工作站,资产安全保障,供软件中心,各种软件插件一键获取,且即开即用,使用灵活&am…...
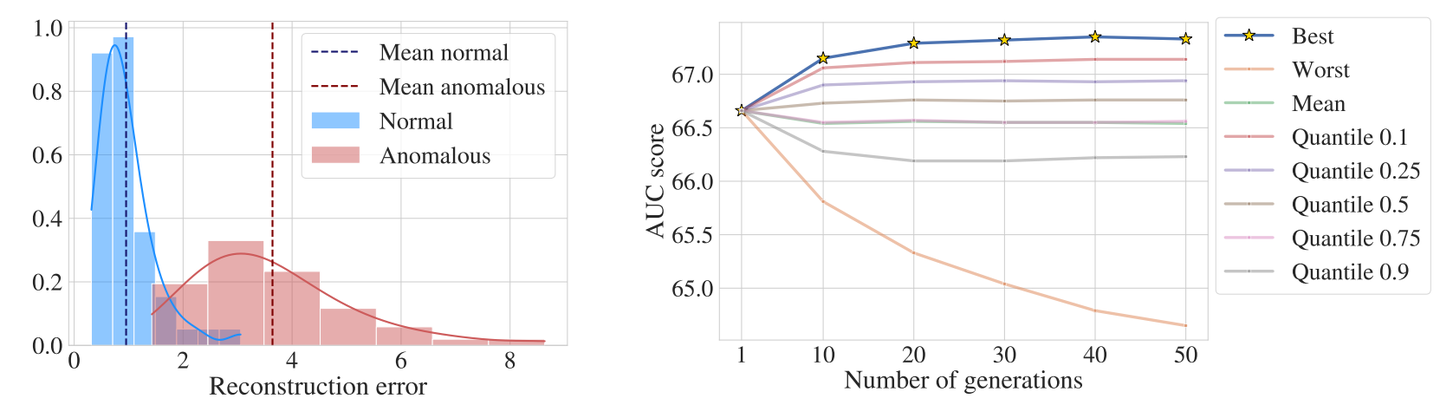
ICCV 2023 | MoCoDAD:一种基于人体骨架的运动条件扩散模型,实现高效视频异常检测
论文链接: https://arxiv.org/abs/2307.07205 视频异常检测(Video Anomaly Detection,VAD)扩展自经典的异常检测任务,由于异常情况样本非常少见,因此经典的异常检测通常被定义为一类分类问题(On…...
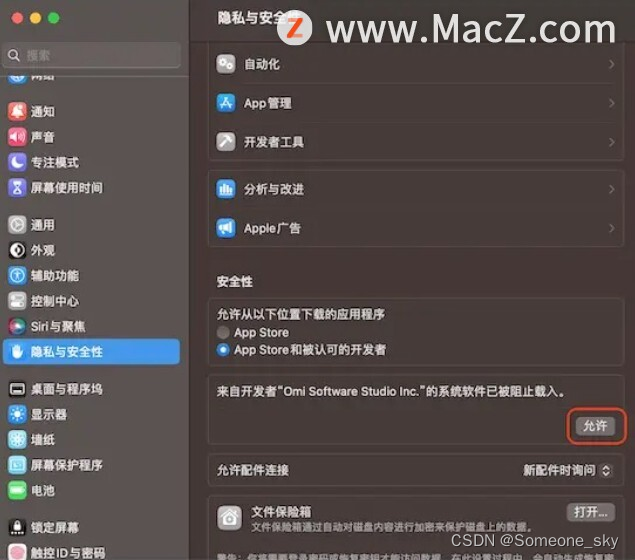
Mac电脑怎么使用NTFS磁盘管理器 NTFS磁盘详细使用教程
Mac是可以识别NTFS硬盘的,但是macOS系统虽然能够正确识别NTFS硬盘,但只支持读取,不支持写入。换句话说,Mac不支持对NTFS硬盘进行编辑、创建、删除等写入操作,比如将Mac里的文件拖入NTFS硬盘,在NTFS硬盘里新…...
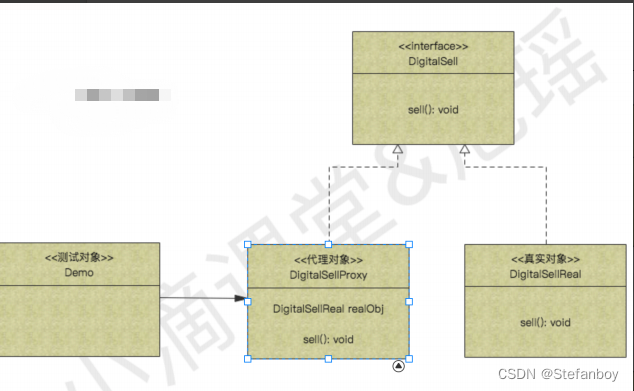
Java设计模式-结构性设计模式(代理设计模式)
简介 为其他对象提供⼀种代理以控制对这个对象的访问,属于结构型模式。客户端并不直接调⽤实际的对象,⽽是通过调⽤代理,来间接的调⽤实际的对象应用场景 各⼤数码专营店,代理⼚商进⾏销售对应的产品,代理商持有真正的…...

线性空间、子空间、基、基坐标、过渡矩阵
线性空间的定义 满足加法和数乘封闭。也就是该空间的所有向量都满足乘一个常数后或者和其它向量相加后仍然在这个空间里。进一步可以理解为该空间中的所有向量满足加法和数乘的组合封闭。即若 V 是一个线性空间,则首先需满足: 注:线性空间里面…...
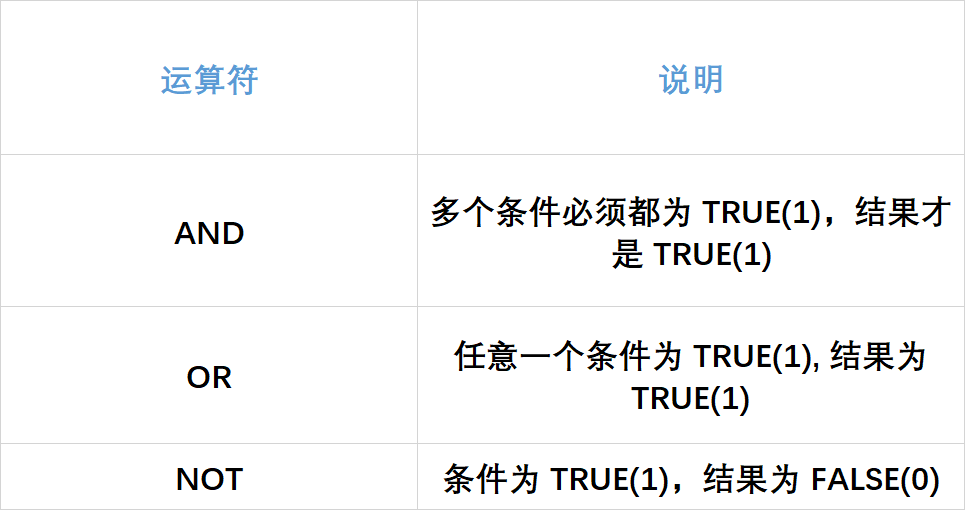
【MySQL】CRUD (增删改查) 基础
CRUD(增删改查)基础 一. CRUD二. 新增 (Create)1. 单行数据 全列插入2. 多行数据 指定列插入 三. 查询(Retrieve)1. 全列查询2. 指定列查询3. 查询字段为表达式4. 别名5. 去重:DISTINCT6. 排序…...

Socks5代理IP:保障跨境电商的网络安全
在数字化时代,跨境电商已成为全球商业的重要一环。然而,随着其发展壮大,网络安全问题也逐渐浮出水面。为了确保跨境电商的安全和隐私,Socks5代理IP技术成为了一项不可或缺的工具。本文将深入探讨Socks5代理IP在跨境电商中的应用&a…...
macOS通过钥匙串访问找回WiFi密码
如果您忘记了Mac电脑上的WiFi密码,可以通过钥匙串访问来找回它。具体步骤如下: 1.打开Mac电脑的“启动台”,然后在其他文件中找到“钥匙串访问”。 2.运行“钥匙串访问”应用程序,点击左侧的“系统”,然后在右侧找到…...
Debian11之稳定版本Jenkins安装
官方网址 系统要求 机器要求 256 MB 内存,建议大于 512 MB 10 GB 的硬盘空间(用于 Jenkins 和 Docker 镜像)软件要求 Java 8 ( JRE 或者 JDK 都可以) Docker (导航到网站顶部的Get Docker链接以访问适合您平台的Docker下载安装…...

kakfa 3.5 kafka服务端处理消费者客户端拉取数据请求源码
一、服务端接收消费者拉取数据的方法二、遍历请求中需要拉取数据的主题分区集合,分别执行查询数据操作,1、会选择合适的副本读取本地日志数据(2.4版本后支持主题分区多副本下的读写分离) 三、会判断当前请求是主题分区Follower发送的拉取数据请求还是消费…...

【Linux】进程概念I --操作系统概念与冯诺依曼体系结构
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法…感兴趣就关注我吧!你定不会失望。 本篇导航 1. 冯诺依曼体系结构为什么这样设计? 2. 操作系统概念为什么我们需要操作系统呢?操作系统怎么进行管理? 计算机是由两部分组…...
BRAM/URAM资源介绍
BRAM/URAM资源简介 Bram和URAM都是FPGA(现场可编程门阵列)中的RAM资源。 Bram是Block RAM的缩写,是Xilinx FPGA中常见的RAM资源之一,也是最常用的资源之一。它是一种单独的RAM模块,通常用于存储大量的数据࿰…...

分享一个基于python的个性推荐餐厅系统源码 餐厅管理系统代码
💕💕作者:计算机源码社 💕💕个人简介:本人七年开发经验,擅长Java、Python、PHP、.NET、Node.js、微信小程序、爬虫、大数据等,大家有这一块的问题可以一起交流! …...

Mysql5.7开启SSL认证且支持Springboot客户端验证
Mysql5.7开启SSL认证 一、查看服务端mysql环境 1.查看是否开启了ssl,"have_ssl" 为YES的时候,数据库是开启加密连接方式的。 show global variables like %ssl%;2.查看数据库版本 select version();3.查看数据库端口 show variables like port;4.查看数据库存放…...

微信小程序的页面滚动事件监听
微信小程序中可以通过 Page 的 onPageScroll 方法来监听页面滚动事件。具体步骤如下: 在页面的 onLoad 方法中注册页面滚动事件监听器: Page({onLoad: function () {wx.pageScrollTo({scrollTop: 0,duration: 0});wx.showLoading({title: 加载中,});wx…...

数据可视化:四大发明的现代转化引擎
在科技和工业的蓬勃发展中,中国的四大发明——造纸术、印刷术、火药和指南针,早已不再是古代创新的象征,而是催生了众多衍生行业的崭新可能性。其中,数据可视化技术正成为这些行业的一颗璀璨明珠,开启了全新的时代。 1…...

HarmonyOS实现几种常见图片点击效果
一. 样例介绍 HarmonyOS提供了常用的图片、图片帧动画播放器组件,开发者可以根据实际场景和开发需求,实现不同的界面交互效果,包括:点击阴影效果、点击切换状态、点击动画效果、点击切换动效。 相关概念 image组件:图片…...
)
3D视觉测量:计算两个平面之间的夹角(附源码)
文章目录 1. 基本内容2. 代码实现文章目录:形位公差测量关键内容:通过视觉方法实现平面之间夹角的计算1. 基本内容 要计算两个平面之间的夹角,首先需要知道这两个平面的法向量。假设有两个平面,它们的法向量分别为 N 1 和 N 2 N_1 和 N_2...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...
