用python实现基本数据结构【04/4】

说明
如果需要用到这些知识却没有掌握,则会让人感到沮丧,也可能导致面试被拒。无论是花几天时间“突击”,还是利用零碎的时间持续学习,在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢?列表、字典、集合,还有……栈?Python 有栈吗?本系列文章将给出详细拼图。
13章: Binary Tree
The binary Tree: 二叉树,每个节点做多只有两个子节点
class _BinTreeNode:def __init__(self, data):self.data = dataself.left = Noneself.right = None# 三种depth-first遍历
def preorderTrav(subtree):""" 先(根)序遍历"""if subtree is not None:print(subtree.data)preorderTrav(subtree.left)preorderTrav(subtree.right)def inorderTrav(subtree):""" 中(根)序遍历"""if subtree is not None:preorderTrav(subtree.left)print(subtree.data)preorderTrav(subtree.right)def postorderTrav(subtree):""" 后(根)序遍历"""if subtree is not None:preorderTrav(subtree.left)preorderTrav(subtree.right)print(subtree.data)# 宽度优先遍历(bradth-First Traversal): 一层一层遍历, 使用queue
def breadthFirstTrav(bintree):from queue import Queue # py3q = Queue()q.put(bintree)while not q.empty():node = q.get()print(node.data)if node.left is not None:q.put(node.left)if node.right is not None:q.put(node.right)class _ExpTreeNode:__slots__ = ('element', 'left', 'right')def __init__(self, data):self.element = dataself.left = Noneself.right = Nonedef __repr__(self):return '<_ExpTreeNode: {} {} {}>'.format(self.element, self.left, self.right)from queue import Queue
class ExpressionTree:"""表达式树: 操作符存储在内节点操作数存储在叶子节点的二叉树。(符号树真难打出来)*/ \+ -/ \ / \9 3 8 4(9+3) * (8-4)Expression Tree Abstract Data Type,可以实现二元操作符ExpressionTree(expStr): user string as constructor paramevaluate(varDict): evaluates the expression and returns the numeric resulttoString(): constructs and retutns a string represention of the expressionUsage:vars = {'a': 5, 'b': 12}expTree = ExpressionTree("(a/(b-3))")print('The result = ', expTree.evaluate(vars))"""def __init__(self, expStr):self._expTree = Noneself._buildTree(expStr)def evaluate(self, varDict):return self._evalTree(self._expTree, varDict)def __str__(self):return self._buildString(self._expTree)def _buildString(self, treeNode):""" 在一个子树被遍历之前添加做括号,在子树被遍历之后添加右括号 """# print(treeNode)if treeNode.left is None and treeNode.right is None:return str(treeNode.element) # 叶子节点是操作数直接返回else:expStr = '('expStr += self._buildString(treeNode.left)expStr += str(treeNode.element)expStr += self._buildString(treeNode.right)expStr += ')'return expStrdef _evalTree(self, subtree, varDict):# 是不是叶子节点, 是的话说明是操作数,直接返回if subtree.left is None and subtree.right is None:# 操作数是合法数字吗if subtree.element >= '0' and subtree.element <= '9':return int(subtree.element)else: # 操作数是个变量assert subtree.element in varDict, 'invalid variable.'return varDict[subtree.element]else: # 操作符则计算其子表达式lvalue = self._evalTree(subtree.left, varDict)rvalue = self._evalTree(subtree.right, varDict)print(subtree.element)return self._computeOp(lvalue, subtree.element, rvalue)def _computeOp(self, left, op, right):assert opop_func = {'+': lambda left, right: left + right, # or import operator, operator.add'-': lambda left, right: left - right,'*': lambda left, right: left * right,'/': lambda left, right: left / right,'%': lambda left, right: left % right,}return op_func[op](left, right)def _buildTree(self, expStr):expQ = Queue()for token in expStr: # 遍历表达式字符串的每个字符expQ.put(token)self._expTree = _ExpTreeNode(None) # 创建root节点self._recBuildTree(self._expTree, expQ)def _recBuildTree(self, curNode, expQ):token = expQ.get()if token == '(':curNode.left = _ExpTreeNode(None)self._recBuildTree(curNode.left, expQ)# next token will be an operator: + = * / %curNode.element = expQ.get()curNode.right = _ExpTreeNode(None)self._recBuildTree(curNode.right, expQ)# the next token will be ')', remmove itexpQ.get()else: # the token is a digit that has to be converted to an int.curNode.element = tokenvars = {'a': 5, 'b': 12}
expTree = ExpressionTree("((2*7)+8)")
print(expTree)
print('The result = ', expTree.evaluate(vars))
Heap(堆):二叉树最直接的一个应用就是实现堆。堆就是一颗完全二叉树,最大堆的非叶子节点的值都比孩子大,最小堆的非叶子结点的值都比孩子小。 python内置了heapq模块帮助我们实现堆操作,比如用内置的heapq模块实现个堆排序:
# 使用python内置的heapq实现heap sort def heapsort(iterable):from heapq import heappush, heappoph = []for value in iterable:heappush(h, value)return [heappop(h) for i in range(len(h))]
但是一般实现堆的时候实际上并不是用数节点来实现的,而是使用数组实现,效率比较高。为什么可以用数组实现呢?因为完全二叉树的性质, 可以用下标之间的关系表示节点之间的关系,MaxHeap的docstring中已经说明了
class MaxHeap:"""Heaps:完全二叉树,最大堆的非叶子节点的值都比孩子大,最小堆的非叶子结点的值都比孩子小Heap包含两个属性,order property 和 shape property(a complete binary tree),在插入一个新节点的时候,始终要保持这两个属性插入操作:保持堆属性和完全二叉树属性, sift-up 操作维持堆属性extract操作:只获取根节点数据,并把树最底层最右节点copy到根节点后,sift-down操作维持堆属性用数组实现heap,从根节点开始,从上往下从左到右给每个节点编号,则根据完全二叉树的性质,给定一个节点i, 其父亲和孩子节点的编号分别是:parent = (i-1) // 2left = 2 * i + 1rgiht = 2 * i + 2使用数组实现堆一方面效率更高,节省树节点的内存占用,一方面还可以避免复杂的指针操作,减少调试难度。"""def __init__(self, maxSize):self._elements = Array(maxSize) # 第二章实现的Array ADTself._count = 0def __len__(self):return self._countdef capacity(self):return len(self._elements)def add(self, value):assert self._count < self.capacity(), 'can not add to full heap'self._elements[self._count] = valueself._count += 1self._siftUp(self._count - 1)self.assert_keep_heap() # 确定每一步add操作都保持堆属性def extract(self):assert self._count > 0, 'can not extract from an empty heap'value = self._elements[0] # save root valueself._count -= 1self._elements[0] = self._elements[self._count] # 最右下的节点放到root后siftDownself._siftDown(0)self.assert_keep_heap()return valuedef _siftUp(self, ndx):if ndx > 0:parent = (ndx - 1) // 2# print(ndx, parent)if self._elements[ndx] > self._elements[parent]: # swapself._elements[ndx], self._elements[parent] = self._elements[parent], self._elements[ndx]self._siftUp(parent) # 递归def _siftDown(self, ndx):left = 2 * ndx + 1right = 2 * ndx + 2# determine which node contains the larger valuelargest = ndxif (left < self._count andself._elements[left] >= self._elements[largest] andself._elements[left] >= self._elements[right]): # 原书这个地方没写实际上找的未必是largestlargest = leftelif right < self._count and self._elements[right] >= self._elements[largest]:largest = rightif largest != ndx:self._elements[ndx], self._elements[largest] = self._elements[largest], self._elements[ndx]self._siftDown(largest)def __repr__(self):return ' '.join(map(str, self._elements))def assert_keep_heap(self):""" 我加了这个函数是用来验证每次add或者extract之后,仍保持最大堆的性质"""_len = len(self)for i in range(0, int((_len-1)/2)): # 内部节点(非叶子结点)l = 2 * i + 1r = 2 * i + 2if l < _len and r < _len:assert self._elements[i] >= self._elements[l] and self._elements[i] >= self._elements[r]def test_MaxHeap():""" 最大堆实现的单元测试用例 """_len = 10h = MaxHeap(_len)for i in range(_len):h.add(i)h.assert_keep_heap()for i in range(_len):# 确定每次出来的都是最大的数字,添加的时候是从小到大添加的assert h.extract() == _len-i-1test_MaxHeap()def simpleHeapSort(theSeq):""" 用自己实现的MaxHeap实现堆排序,直接修改原数组实现inplace排序"""if not theSeq:return theSeq_len = len(theSeq)heap = MaxHeap(_len)for i in theSeq:heap.add(i)for i in reversed(range(_len)):theSeq[i] = heap.extract()return theSeqdef test_simpleHeapSort():""" 用一些测试用例证明实现的堆排序是可以工作的 """def _is_sorted(seq):for i in range(len(seq)-1):if seq[i] > seq[i+1]:return Falsereturn Truefrom random import randintassert simpleHeapSort([]) == []for i in range(1000):_len = randint(1, 100)to_sort = []for i in range(_len):to_sort.append(randint(0, 100))simpleHeapSort(to_sort) # 注意这里用了原地排序,直接更改了数组assert _is_sorted(to_sort)test_simpleHeapSort()
14章: Search Trees
二叉差找树性质:对每个内部节点V, 1. 所有key小于V.key的存储在V的左子树。 2. 所有key大于V.key的存储在V的右子树 对BST进行中序遍历会得到升序的key序列
class _BSTMapNode:__slots__ = ('key', 'value', 'left', 'right')def __init__(self, key, value):self.key = keyself.value = valueself.left = Noneself.right = Nonedef __repr__(self):return '<{}:{}> left:{}, right:{}'.format(self.key, self.value, self.left, self.right)__str__ = __repr__class BSTMap:""" BST,树节点包含key可payload。用BST来实现之前用hash实现过的Map ADT.性质:对每个内部节点V,1.对于节点V,所有key小于V.key的存储在V的左子树。2.所有key大于V.key的存储在V的右子树对BST进行中序遍历会得到升序的key序列"""def __init__(self):self._root = Noneself._size = 0self._rval = None # 作为remove的返回值def __len__(self):return self._sizedef __iter__(self):return _BSTMapIterator(self._root, self._size)def __contains__(self, key):return self._bstSearch(self._root, key) is not Nonedef valueOf(self, key):node = self._bstSearch(self._root, key)assert node is not None, 'Invalid map key.'return node.valuedef _bstSearch(self, subtree, target):if subtree is None: # 递归出口,遍历到树底没有找到key或是空树return Noneelif target < subtree.key:return self._bstSearch(subtree.left, target)elif target > subtree.key:return self._bstSearch(subtree.right, target)return subtree # 返回引用def _bstMinumum(self, subtree):""" 顺着树一直往左下角递归找就是最小的,向右下角递归就是最大的 """if subtree is None:return Noneelif subtree.left is None:return subtreeelse:return subtree._bstMinumum(self, subtree.left)def add(self, key, value):""" 添加或者替代一个key的value, O(N) """node = self._bstSearch(self._root, key)if node is not None: # if key already exists, update valuenode.value = valuereturn Falseelse: # insert a new entryself._root = self._bstInsert(self._root, key, value)self._size += 1return Truedef _bstInsert(self, subtree, key, value):""" 新的节点总是插入在树的叶子结点上 """if subtree is None:subtree = _BSTMapNode(key, value)elif key < subtree.key:subtree.left = self._bstInsert(subtree.left, key, value)elif key > subtree.key:subtree.right = self._bstInsert(subtree.right, key, value)# 注意这里没有else语句了,应为在被调用处add函数里先判断了是否有重复keyreturn subtreedef remove(self, key):""" O(N)被删除的节点分为三种:1.叶子结点:直接把其父亲指向该节点的指针置None2.该节点有一个孩子: 删除该节点后,父亲指向一个合适的该节点的孩子3.该节点有俩孩子:(1)找到要删除节点N和其后继S(中序遍历后该节点下一个)(2)复制S的key到N(3)从N的右子树中删除后继S(即在N的右子树中最小的)"""assert key in self, 'invalid map key'self._root = self._bstRemove(self._root, key)self._size -= 1return self._rvaldef _bstRemove(self, subtree, target):# search for the item in the treeif subtree is None:return subtreeelif target < subtree.key:subtree.left = self._bstRemove(subtree.left, target)return subtreeelif target > subtree.key:subtree.right = self._bstRemove(subtree.right, target)return subtreeelse: # found the node containing the itemself._rval = subtree.valueif subtree.left is None and subtree.right is None:# 叶子nodereturn Noneelif subtree.left is None or subtree.right is None:# 有一个孩子节点if subtree.left is not None:return subtree.leftelse:return subtree.rightelse: # 有俩孩子节点successor = self._bstMinumum(subtree.right)subtree.key = successor.keysubtree.value = successor.valuesubtree.right = self._bstRemove(subtree.right, successor.key)return subtreedef __repr__(self):return '->'.join([str(i) for i in self])def assert_keep_bst_property(self, subtree):""" 写这个函数为了验证add和delete操作始终维持了bst的性质 """if subtree is None:returnif subtree.left is not None and subtree.right is not None:assert subtree.left.value <= subtree.valueassert subtree.right.value >= subtree.valueself.assert_keep_bst_property(subtree.left)self.assert_keep_bst_property(subtree.right)elif subtree.left is None and subtree.right is not None:assert subtree.right.value >= subtree.valueself.assert_keep_bst_property(subtree.right)elif subtree.left is not None and subtree.right is None:assert subtree.left.value <= subtree.valueself.assert_keep_bst_property(subtree.left)class _BSTMapIterator:def __init__(self, root, size):self._theKeys = Array(size)self._curItem = 0self._bstTraversal(root)self._curItem = 0def __iter__(self):return selfdef __next__(self):if self._curItem < len(self._theKeys):key = self._theKeys[self._curItem]self._curItem += 1return keyelse:raise StopIterationdef _bstTraversal(self, subtree):if subtree is not None:self._bstTraversal(subtree.left)self._theKeys[self._curItem] = subtree.keyself._curItem += 1self._bstTraversal(subtree.right)def test_BSTMap():l = [60, 25, 100, 35, 17, 80]bst = BSTMap()for i in l:bst.add(i)def test_HashMap():""" 之前用来测试用hash实现的map,改为用BST实现的Map测试 """# h = HashMap()h = BSTMap()assert len(h) == 0h.add('a', 'a')assert h.valueOf('a') == 'a'assert len(h) == 1a_v = h.remove('a')assert a_v == 'a'assert len(h) == 0h.add('a', 'a')h.add('b', 'b')assert len(h) == 2assert h.valueOf('b') == 'b'b_v = h.remove('b')assert b_v == 'b'assert len(h) == 1h.remove('a')assert len(h) == 0_len = 10for i in range(_len):h.add(str(i), i)assert len(h) == _lenfor i in range(_len):assert str(i) in hfor i in range(_len):print(len(h))print('bef', h)_ = h.remove(str(i))assert _ == iprint('aft', h)print(len(h))assert len(h) == 0test_HashMap()相关文章:

用python实现基本数据结构【04/4】
说明 如果需要用到这些知识却没有掌握,则会让人感到沮丧,也可能导致面试被拒。无论是花几天时间“突击”,还是利用零碎的时间持续学习,在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢?列表、字典、集…...

“必抓!”算法
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。今天就来聊聊这些十分重要的“必抓!”算法吧~ 你可以从以下几个方面进行创作(仅供参考) 一ÿ…...

【监控系统】Promethus整合Alertmanager监控告警邮件通知
【监控系统】Promethus整合Alertmanager监控告警邮件通知 Alertmanager是一种开源软件,用于管理和报警监视警报。它与Prometheus紧密集成,后者是一种流行的开源监视和警报系统。Alertmanager从多个源接收警报和通知,并根据一组配置规则来决定…...
【韩顺平】Linux基础
目录 1.网络连接三种方式 1.1 桥接模式:虚拟系统可以和外部系统通讯,但是容易造成IP冲突【1-225】 1.2 NAT模式:网络地址转换模式。虚拟系统可以和外部系统通讯,不造成IP冲突。 1.3 主机模式:独立的系统。 2.虚拟机…...

好奇一下各个大模型对华为mate60系列的看法
目前华为Mate60系列手机已上市并获抢购,个人觉得很不错,很好奇各个AI大模型对此事的看法,于是对chatGPT、文心一言、讯飞星火进行了一下粗浅的测试。 题目一(看看三个模型的综合分析能力) “目前华为Mate60系列手机已…...

UMA 2 - Unity Multipurpose Avatar☀️五.如何使用别人的Recipe和创建自己的服饰Recipe
文章目录 🟥 使用别人的Recipe1️⃣ 导入UMA资源效果展示2️⃣ 更新Library3️⃣ 试一下吧🟧 创建自己的服饰Recipe1️⃣ 创建自己的服饰Recipe2️⃣ 选择应用到的Base Recipe3️⃣ 指定显示名 / 佩戴位置 / 隐藏部位4️⃣ 给该服饰Recipe指定Slot / Overlay🚩 赋予Slot�…...

代码随想录训练营第五十六天| 583. 两个字符串的删除操作 、72. 编辑距离
583. 两个字符串的删除操作 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //583.两个字符串的删除操作 int minDistance(string word1, string word2) {//step1 构建dp数组,dp[i][j]的含义是要使以i-1为结尾的word1和以j-1为结尾的word2//删除其元…...

hive解决了什么问题
hive出现的原因 Hive 出现的原因主要有以下几个: 传统数据仓库无法处理大规模数据:传统的数据仓库通常采用关系型数据库作为底层存储,这种数据库在处理大规模数据时效率较低。MapReduce 难以使用:MapReduce 是一种分布式计算框架…...

Lumion 和 Enscape 应该选择怎样的笔记本电脑?
Lumion 和 Enscape实时渲染对配置要求高,本地配置不够,如何快速解决: 本地普通电脑可一键申请高性能工作站,资产安全保障,供软件中心,各种软件插件一键获取,且即开即用,使用灵活&am…...
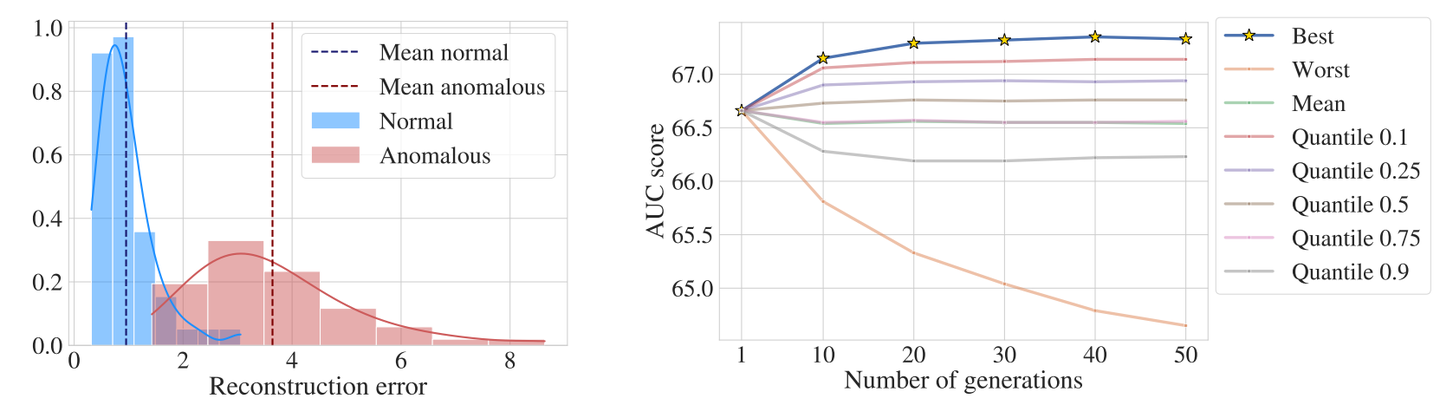
ICCV 2023 | MoCoDAD:一种基于人体骨架的运动条件扩散模型,实现高效视频异常检测
论文链接: https://arxiv.org/abs/2307.07205 视频异常检测(Video Anomaly Detection,VAD)扩展自经典的异常检测任务,由于异常情况样本非常少见,因此经典的异常检测通常被定义为一类分类问题(On…...
Mac电脑怎么使用NTFS磁盘管理器 NTFS磁盘详细使用教程
Mac是可以识别NTFS硬盘的,但是macOS系统虽然能够正确识别NTFS硬盘,但只支持读取,不支持写入。换句话说,Mac不支持对NTFS硬盘进行编辑、创建、删除等写入操作,比如将Mac里的文件拖入NTFS硬盘,在NTFS硬盘里新…...
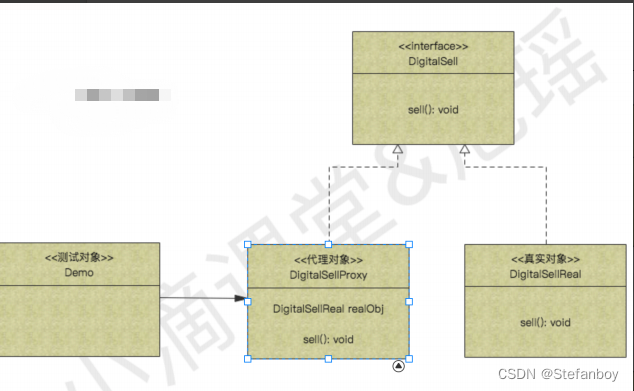
Java设计模式-结构性设计模式(代理设计模式)
简介 为其他对象提供⼀种代理以控制对这个对象的访问,属于结构型模式。客户端并不直接调⽤实际的对象,⽽是通过调⽤代理,来间接的调⽤实际的对象应用场景 各⼤数码专营店,代理⼚商进⾏销售对应的产品,代理商持有真正的…...

线性空间、子空间、基、基坐标、过渡矩阵
线性空间的定义 满足加法和数乘封闭。也就是该空间的所有向量都满足乘一个常数后或者和其它向量相加后仍然在这个空间里。进一步可以理解为该空间中的所有向量满足加法和数乘的组合封闭。即若 V 是一个线性空间,则首先需满足: 注:线性空间里面…...
【MySQL】CRUD (增删改查) 基础
CRUD(增删改查)基础 一. CRUD二. 新增 (Create)1. 单行数据 全列插入2. 多行数据 指定列插入 三. 查询(Retrieve)1. 全列查询2. 指定列查询3. 查询字段为表达式4. 别名5. 去重:DISTINCT6. 排序…...

Socks5代理IP:保障跨境电商的网络安全
在数字化时代,跨境电商已成为全球商业的重要一环。然而,随着其发展壮大,网络安全问题也逐渐浮出水面。为了确保跨境电商的安全和隐私,Socks5代理IP技术成为了一项不可或缺的工具。本文将深入探讨Socks5代理IP在跨境电商中的应用&a…...
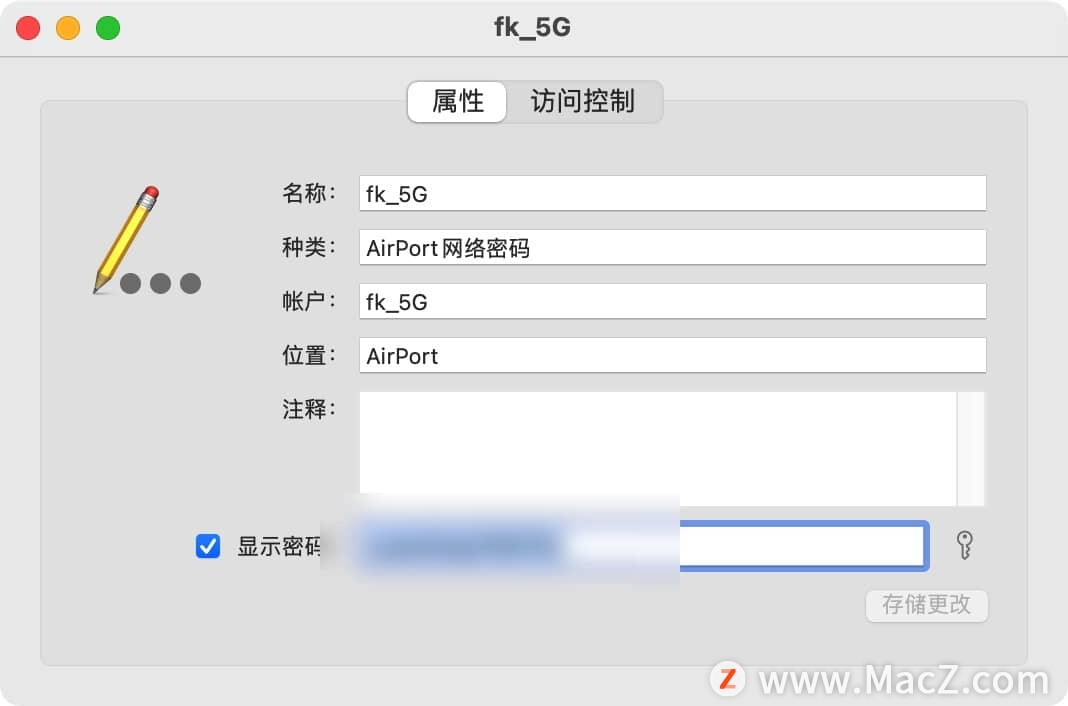
macOS通过钥匙串访问找回WiFi密码
如果您忘记了Mac电脑上的WiFi密码,可以通过钥匙串访问来找回它。具体步骤如下: 1.打开Mac电脑的“启动台”,然后在其他文件中找到“钥匙串访问”。 2.运行“钥匙串访问”应用程序,点击左侧的“系统”,然后在右侧找到…...
Debian11之稳定版本Jenkins安装
官方网址 系统要求 机器要求 256 MB 内存,建议大于 512 MB 10 GB 的硬盘空间(用于 Jenkins 和 Docker 镜像)软件要求 Java 8 ( JRE 或者 JDK 都可以) Docker (导航到网站顶部的Get Docker链接以访问适合您平台的Docker下载安装…...

kakfa 3.5 kafka服务端处理消费者客户端拉取数据请求源码
一、服务端接收消费者拉取数据的方法二、遍历请求中需要拉取数据的主题分区集合,分别执行查询数据操作,1、会选择合适的副本读取本地日志数据(2.4版本后支持主题分区多副本下的读写分离) 三、会判断当前请求是主题分区Follower发送的拉取数据请求还是消费…...

【Linux】进程概念I --操作系统概念与冯诺依曼体系结构
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法…感兴趣就关注我吧!你定不会失望。 本篇导航 1. 冯诺依曼体系结构为什么这样设计? 2. 操作系统概念为什么我们需要操作系统呢?操作系统怎么进行管理? 计算机是由两部分组…...
BRAM/URAM资源介绍
BRAM/URAM资源简介 Bram和URAM都是FPGA(现场可编程门阵列)中的RAM资源。 Bram是Block RAM的缩写,是Xilinx FPGA中常见的RAM资源之一,也是最常用的资源之一。它是一种单独的RAM模块,通常用于存储大量的数据࿰…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
