Codeforces Round 855 (Div 3)(A - F)
Codeforces Round 855 (Div. 3)(A - F)
Codeforces Round 855 (Div. 3)
A. Is It a Cat?(思维)
思路:先把所有字母变成小写方便判断 , 然后把每一部分取一个字母出来 , 判断和‘meow’是否相同即可。
复杂度 O ( n ) 复杂度O(n) 复杂度O(n)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int n , t;string s;bool judge(string s){string now;for(int i = 0 ; i < n ; i ++) if(i == 0 || s[i] != s[i - 1]) now += s[i];return now == "meow";
}signed main(){IOScin >> t;while(t --) {cin >> n >> s;for(int i = 0 ; i < n ; i ++) s[i] = tolower(s[i]);if(judge(s)) {cout << "YES\n";} else {cout << "NO\n";}}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
B. Count the Number of Pairs(模拟 + 贪心)
思路:先贪心的把能合并的合并掉 , 然后对于不能合并的进行操作即可。
复杂度 O ( n ) 复杂度O(n) 复杂度O(n)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int cnt1[30] , cnt2[30];
int t , n , k;
string s;
signed main(){IOScin >> t;while(t --){cin >> n >> k;cin >> s;for(int i = 0 ; i < n ; i ++){if(s[i] >= 'a' && s[i] <= 'z') cnt1[s[i] - 'a' + 1] += 1;else cnt2[s[i] - 'A' + 1] += 1;}int res = 0;for(int i = 1 ; i <= 26 ; i ++){int now = min(cnt1[i] , cnt2[i]);res += now;cnt1[i] -= now;cnt2[i] -= now;}for(int i = 1 ; i <= 26 ; i ++){int now = cnt1[i] / 2;if(now <= k){k -= now;res += now;} else {res += k;k = 0;break;}}for(int i = 1 ; i <= 26 ; i ++){int now = cnt2[i] / 2;if(now <= k){k -= now;res += now;} else {res += k;k = 0;break;}} for(int i = 1 ; i <= 26 ; i ++) cnt1[i] = cnt2[i] = 0;cout << res << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
C. Powering the Hero(优先队列)
思路:模拟一下不难发现 , 每次取走英雄牌的时候要在前面没使用的附加牌中选择一张力量值最大的 , 用优先队列维护即可。
复杂度 O ( n l o g n ) 复杂度O(nlogn) 复杂度O(nlogn)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n , now;signed main(){IOScin >> t;while(t --){cin >> n;priority_queue<int , vector<int> , less<int>> q;int res = 0;for(int i = 1 ; i <= n ; i ++){cin >> now;if(now) {q.push(now);} else {if(q.size()){res += q.top();q.pop();}}}cout << res << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
D. Remove Two Letters(思维)
思路:删除两个连续字符 ,对于任意三个字符来说 , 删除 1 , 2 位置的剩余 3 号位置 ,删除 2 , 3 号位置剩余 1 号位置 , 如果 1 3 号位置相同 , 则剩余字符串必定相同 。 即 i 号字符如果和 (i + 2) 号字符相同 , 那么就会产生一个重复答案 , 考虑最多有 n - 1 个答案 , 从中减去重复答案即可。
复杂度 O ( n ) 复杂度O(n) 复杂度O(n)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int t , n;
string s;signed main(){IOScin >> t;while(t --){cin >> n >> s;int res = n - 1;for(int i = 0 ; i < n - 2 ; i ++){if(s[i] == s[i + 2]) res -= 1;}cout << res << "\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
E. Unforgivable Curse(并查集维护集合 , 思维)
思路:考虑 位置 x 可以与 y 进行交换 , 位置 y 可以与 位置 z 进行交换 , 操作三次就相当于在 y 不动的情况下交换了 x , z , 这样在同一个集合中任意两个元素都可以在不影响其余位置的情况下互相交换 ,那么显然一个集合中的字符可以表示任意种类和数目相同的字符串。比较所有集合字符的种类和数量是否相同即可 , 用并查集 和 multiset 维护集合 , 比较即可。
复杂度 O ( n l o g n ) 复杂度O(nlogn) 复杂度O(nlogn)
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e6 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;/*
并查集
*/int t , n , k ;
string st , ed;
int fa[N];int find(int x){if(x == fa[x]) return x;else return fa[x] = find(fa[x]);
}void unionn(int x , int y){int xx = find(x);int yy = find(y);fa[xx] = yy;
}signed main(){IOScin >> t;while(t --){cin >> n >> k;cin >> st >> ed;st = '#' + st;ed = '#' + ed;for(int i = 1 ; i <= n ; i ++) fa[i] = i;for(int i = 1 ; i <= n ; i ++){int x = i + k;int y = i + k + 1;if(x <= n) unionn(i , x);if(y <= n) unionn(i , y);}multiset<char>st1[n + 10] , st2[n + 10];set<int>all;for(int i = 1 ; i <= n ; i ++) {int now = find(i);all.insert(now);st1[now].insert(st[i]);st2[now].insert(ed[i]);}bool tag = 0;for(auto x : all){if(st1[x] != st2[x]) tag = 1;}if(!tag) cout << "YES\n";else cout << "NO\n";}return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
F. Dasha and Nightmares(状态哈希)
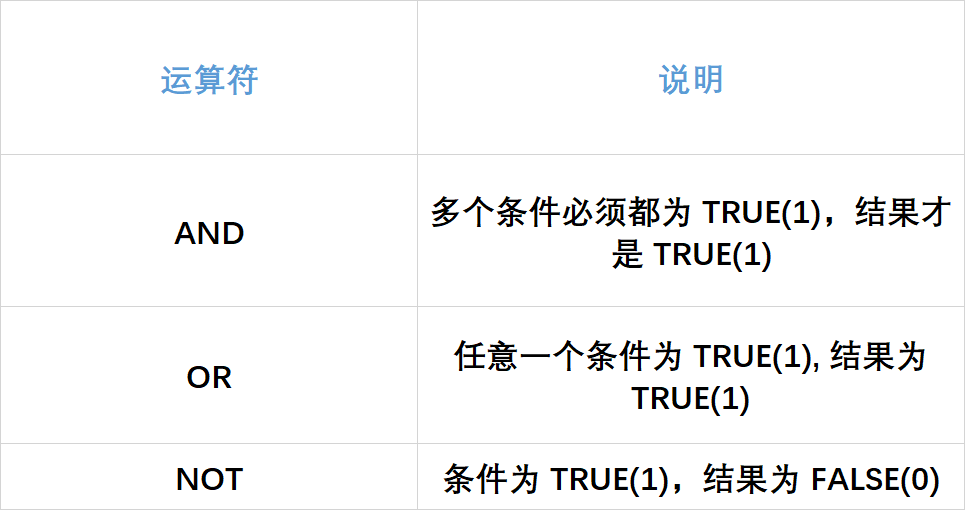
思路:对于三个条件 , 满足了后两个条件第一个条件自然就满足了 , 所以思考如何处理后两个条件。即:
- 恰好出现 25 个字母
- 每个字母出现次数为奇数
我们不妨再次弱化条件 , 思考只有条件三如何去做 。
如果暴力的去做 , 复杂度是O(n ^ 2 * 26) , 显然不能接受 ,对于奇偶性 , 考虑哈希压缩状态 , 把每一个串压缩成一个 26 位的二进制串 , 0 代表当前位是偶数 , 1 代表当前位是奇数 , 那么前面满足条件的状态就是当前二进制状态按位取反后的状态 ,这样就能就做到了O(n)。
考虑加上第二个约束 , 恰好出现了 25 个字母 ,如果我们还是按照前面那样寻找显然是不行的 , 因为二进制位 0 既可以代表 0 次也能代表偶数次 , 考虑维护 26 个哈希表 , 代表第 i 个字母没出现的状态集合 , 遍计数边维护即可。
复杂度 O ( 26 ∗ n ∗ l o g n ) 复杂度O(26*n*logn) 复杂度O(26∗n∗logn)
由于带log复杂度比较极限 , 需要实现的精细一点 ,用 unordered_map 且每次访问之前判断是否有值 , 避免多次访问空值。
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define IOS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
#define int long long
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
typedef pair<int,int>PII;int n , m;
unordered_map<int , int>mp[30];
int cnt[N][30] , pre[N] , nex[N];
string s;
int res;signed main(){IOScin >> n;for(int i = 1 ; i <= n ; i ++) {cin >> s;m = s.size();for(int j = 0 ; j < m ; j ++) cnt[i][s[j] - 'a' + 1] += 1;for(int j = 0 ; j < 26 ; j ++) {pre[i] += (cnt[i][j + 1] % 2) * (1 << j);nex[i] += (1 - cnt[i][j + 1] % 2) * (1 << j);}}// a - zfor(int i = 1 ; i <= n ; i ++){for(int j = 0 ; j < 26 ; j ++){if(cnt[i][j + 1]) continue;int k = nex[i] - (1 << j);if(mp[j + 1].find(k) != mp[j + 1].end()) res += mp[j + 1][k];mp[j + 1][pre[i]] += 1;}}cout << res << "\n";return 0;
}
//freopen("文件名.in","r",stdin);
//freopen("文件名.out","w",stdout);
相关文章:
(A - F))
Codeforces Round 855 (Div 3)(A - F)
Codeforces Round 855 (Div. 3)(A - F) Codeforces Round 855 (Div. 3) A. Is It a Cat?(思维) 思路:先把所有字母变成小写方便判断 , 然后把每一部分取一个字母出来 , 判断和‘meow’是否相同即可。 复杂度 O ( n…...
:社交媒体金融的未来,真的如此美好吗?)
Friend.tech(FT):社交媒体金融的未来,真的如此美好吗?
Friend.tech(FT)是一个在2023年8月10日正式推出的社交金融平台,它的特点在于允许用户购买和出售创作者的股票(shares),这些股票赋予用户访问创作者内容的权利。FT的推出引发了广泛的关注,吸引了…...
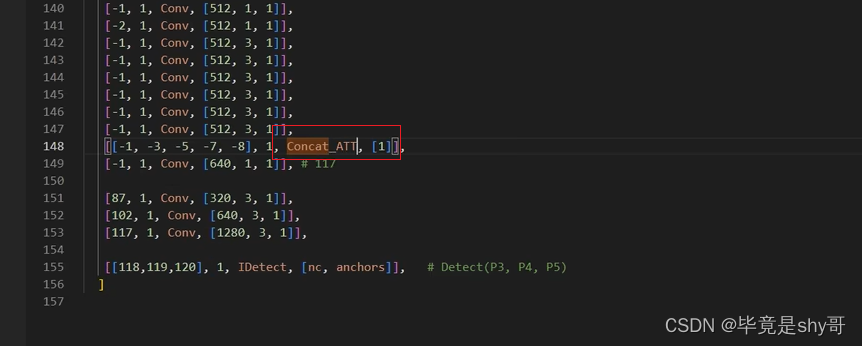
yolov7中Concat之后加注意力模块(最复杂的情况)
1、common.py中找到Concat模块,复制一份 2、要传参进来,dim通道数 3、然后找yolo.py模块,添加 4、yaml里替换 5、和加的位置也有关系...
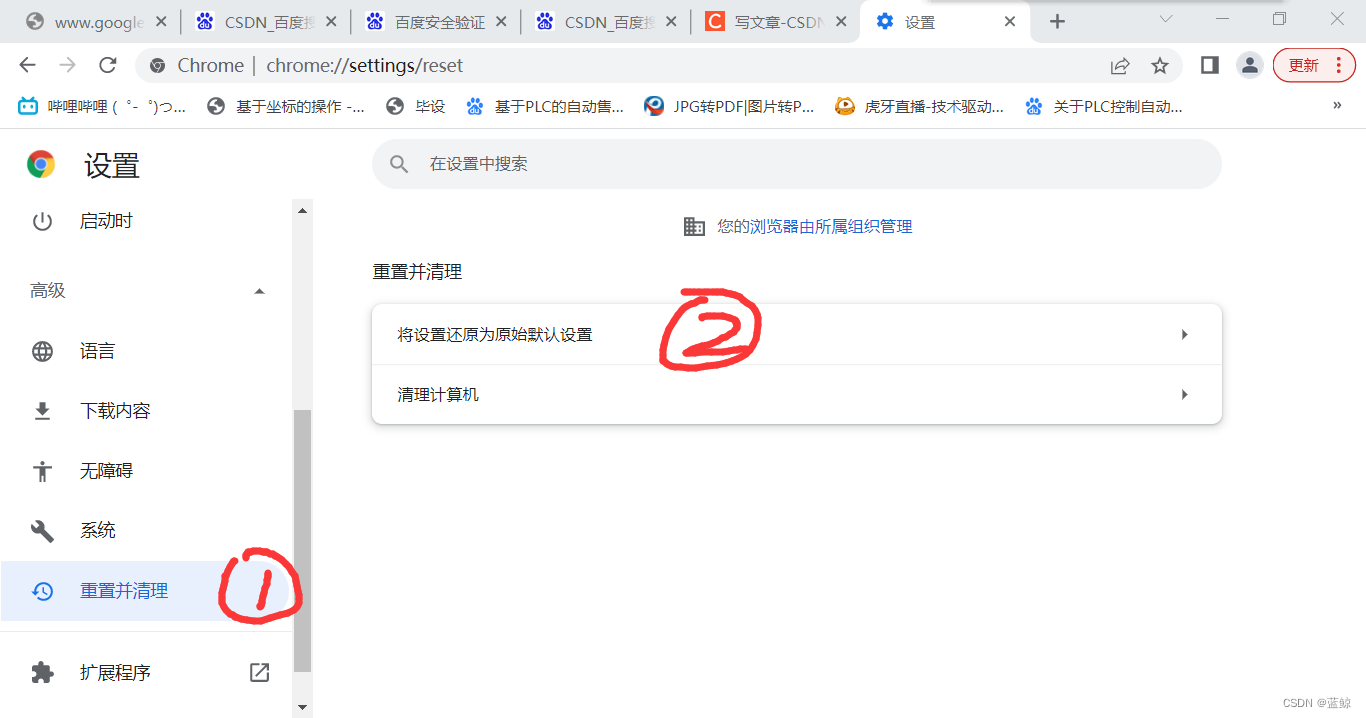
解除百度安全验证
使用chrome浏览器用百度浏览时,一直弹百度安全验证: 在设置里进行重置: 然后重启浏览器就可以了。...
(A - F))
Codeforces Round 731 (Div 3)(A - F)
Codeforces Round 731 (Div. 3)(A - F) Dashboard - Codeforces Round 731 (Div. 3) - Codeforces A. Shortest Path with Obstacle(思维) 思路:显然要计算 A → B 之间的曼哈顿距离 , 要绕开 F 当且仅当 AB形成的直线平行于坐…...
与sorted()函数详解)
Python的sort()与sorted()函数详解
目录 sort()函数 sorted()函数 key参数 区别 sort()函数 sort()方法:该方法用于原地对列表进行排序,即直接在原始列表上进行排序操作,并不返回一个新的列表。 my_l…...

用python实现基本数据结构【04/4】
说明 如果需要用到这些知识却没有掌握,则会让人感到沮丧,也可能导致面试被拒。无论是花几天时间“突击”,还是利用零碎的时间持续学习,在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢?列表、字典、集…...

“必抓!”算法
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。今天就来聊聊这些十分重要的“必抓!”算法吧~ 你可以从以下几个方面进行创作(仅供参考) 一ÿ…...

【监控系统】Promethus整合Alertmanager监控告警邮件通知
【监控系统】Promethus整合Alertmanager监控告警邮件通知 Alertmanager是一种开源软件,用于管理和报警监视警报。它与Prometheus紧密集成,后者是一种流行的开源监视和警报系统。Alertmanager从多个源接收警报和通知,并根据一组配置规则来决定…...
【韩顺平】Linux基础
目录 1.网络连接三种方式 1.1 桥接模式:虚拟系统可以和外部系统通讯,但是容易造成IP冲突【1-225】 1.2 NAT模式:网络地址转换模式。虚拟系统可以和外部系统通讯,不造成IP冲突。 1.3 主机模式:独立的系统。 2.虚拟机…...

好奇一下各个大模型对华为mate60系列的看法
目前华为Mate60系列手机已上市并获抢购,个人觉得很不错,很好奇各个AI大模型对此事的看法,于是对chatGPT、文心一言、讯飞星火进行了一下粗浅的测试。 题目一(看看三个模型的综合分析能力) “目前华为Mate60系列手机已…...

UMA 2 - Unity Multipurpose Avatar☀️五.如何使用别人的Recipe和创建自己的服饰Recipe
文章目录 🟥 使用别人的Recipe1️⃣ 导入UMA资源效果展示2️⃣ 更新Library3️⃣ 试一下吧🟧 创建自己的服饰Recipe1️⃣ 创建自己的服饰Recipe2️⃣ 选择应用到的Base Recipe3️⃣ 指定显示名 / 佩戴位置 / 隐藏部位4️⃣ 给该服饰Recipe指定Slot / Overlay🚩 赋予Slot�…...

代码随想录训练营第五十六天| 583. 两个字符串的删除操作 、72. 编辑距离
583. 两个字符串的删除操作 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //583.两个字符串的删除操作 int minDistance(string word1, string word2) {//step1 构建dp数组,dp[i][j]的含义是要使以i-1为结尾的word1和以j-1为结尾的word2//删除其元…...

hive解决了什么问题
hive出现的原因 Hive 出现的原因主要有以下几个: 传统数据仓库无法处理大规模数据:传统的数据仓库通常采用关系型数据库作为底层存储,这种数据库在处理大规模数据时效率较低。MapReduce 难以使用:MapReduce 是一种分布式计算框架…...

Lumion 和 Enscape 应该选择怎样的笔记本电脑?
Lumion 和 Enscape实时渲染对配置要求高,本地配置不够,如何快速解决: 本地普通电脑可一键申请高性能工作站,资产安全保障,供软件中心,各种软件插件一键获取,且即开即用,使用灵活&am…...
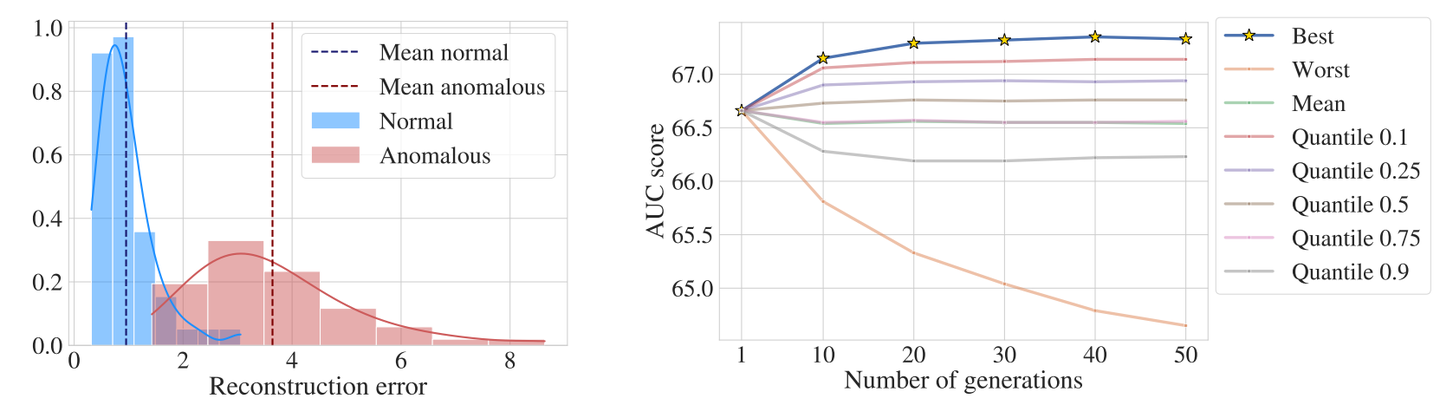
ICCV 2023 | MoCoDAD:一种基于人体骨架的运动条件扩散模型,实现高效视频异常检测
论文链接: https://arxiv.org/abs/2307.07205 视频异常检测(Video Anomaly Detection,VAD)扩展自经典的异常检测任务,由于异常情况样本非常少见,因此经典的异常检测通常被定义为一类分类问题(On…...
Mac电脑怎么使用NTFS磁盘管理器 NTFS磁盘详细使用教程
Mac是可以识别NTFS硬盘的,但是macOS系统虽然能够正确识别NTFS硬盘,但只支持读取,不支持写入。换句话说,Mac不支持对NTFS硬盘进行编辑、创建、删除等写入操作,比如将Mac里的文件拖入NTFS硬盘,在NTFS硬盘里新…...
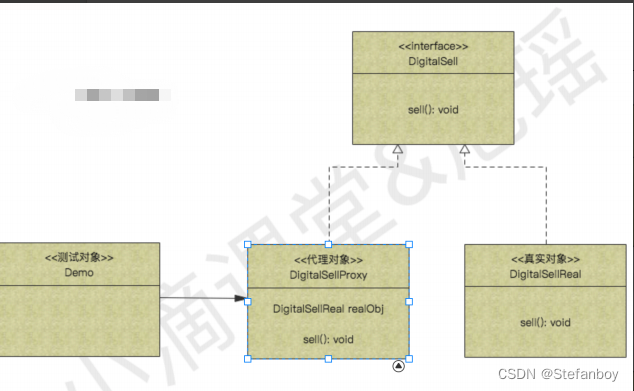
Java设计模式-结构性设计模式(代理设计模式)
简介 为其他对象提供⼀种代理以控制对这个对象的访问,属于结构型模式。客户端并不直接调⽤实际的对象,⽽是通过调⽤代理,来间接的调⽤实际的对象应用场景 各⼤数码专营店,代理⼚商进⾏销售对应的产品,代理商持有真正的…...

线性空间、子空间、基、基坐标、过渡矩阵
线性空间的定义 满足加法和数乘封闭。也就是该空间的所有向量都满足乘一个常数后或者和其它向量相加后仍然在这个空间里。进一步可以理解为该空间中的所有向量满足加法和数乘的组合封闭。即若 V 是一个线性空间,则首先需满足: 注:线性空间里面…...
【MySQL】CRUD (增删改查) 基础
CRUD(增删改查)基础 一. CRUD二. 新增 (Create)1. 单行数据 全列插入2. 多行数据 指定列插入 三. 查询(Retrieve)1. 全列查询2. 指定列查询3. 查询字段为表达式4. 别名5. 去重:DISTINCT6. 排序…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...
