Go-Python-Java-C-LeetCode高分解法-第五周合集
前言
本题解Go语言部分基于 LeetCode-Go
其他部分基于本人实践学习
个人题解GitHub连接:LeetCode-Go-Python-Java-C
Go-Python-Java-C-LeetCode高分解法-第一周合集
Go-Python-Java-C-LeetCode高分解法-第二周合集
Go-Python-Java-C-LeetCode高分解法-第三周合集
Go-Python-Java-C-LeetCode高分解法-第四周合集
本文部分内容来自网上搜集与个人实践。如果任何信息存在错误,欢迎读者批评指正。本文仅用于学习交流,不用作任何商业用途。
29. Divide Two Integers
题目
Given two integersdividendanddivisor, divide two integers without using multiplication, division and mod operator.
Return the quotient after dividingdividendbydivisor.
The integer division should truncate toward zero.
Example 1:
Input: dividend = 10, divisor = 3
Output: 3
Example 2:
Input: dividend = 7, divisor = -3
Output: -2
Note:
- Both dividend and divisor will be 32-bit signed integers.
- The divisor will never be 0.
- Assume we are dealing with an environment which could only store integers within the 32-bit signed integer
range: [−2^31, 2^31 − 1]. For the purpose of this problem, assume that your function returns 2^31 − 1 when the
division result overflows.
题目大意
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。返回被除数 dividend 除以除数
divisor 得到的商。
说明:
- 被除数和除数均为 32 位有符号整数。
- 除数不为 0。
- 假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−2^31, 2^31 − 1]。本题中,如果除法结果溢出,则返回 2^31 − 1。
解题思路
- 给出除数和被除数,要求计算除法运算以后的商。注意值的取值范围在 [−2^31, 2^31 − 1] 之中。超过范围的都按边界计算。
- 这一题可以用二分搜索来做。要求除法运算之后的商,把商作为要搜索的目标。商的取值范围是 [0, dividend],所以从 0
到被除数之间搜索。利用二分,找到(商 + 1 ) * 除数 > 被除数并且 商 * 除数 ≤ 被除数 或者 (商+1)* 除数 ≥ 被除数并且商 *
除数 < 被除数的时候,就算找到了商,其余情况继续二分即可。最后还要注意符号和题目规定的 Int32 取值范围。 - 二分的写法常写错的 3 点:
- low ≤ high (注意二分循环退出的条件是小于等于)
- mid = low + (high-low)>>1 (防止溢出)
- low = mid + 1 ; high = mid - 1 (注意更新 low 和 high 的值,如果更新不对就会死循环)
以下是每个版本的解题思路的详细介绍:
Go 版本
Go 版本的解题思路如下:
-
首先,处理特殊情况,包括被除数(dividend)等于 0,除数(divisor)等于 1,以及避免溢出的情况(例如,被除数为math.MinInt32,除数为-1)。
-
确定最终结果的符号(正数或负数),并将被除数和除数都转换为正数,以便进行位运算。
-
使用二分搜索来找到商。二分搜索的目标是找到一个整数 x,使得
(x + 1) * divisor > dividend且x * divisor ≤ dividend,或者(x + 1) * divisor ≥ dividend且x * divisor < dividend。这个 x 就是我们要找的商。 -
在二分搜索的过程中,确保更新搜索的范围和值,同时处理可能的溢出情况。
-
最后,根据符号和边界情况返回最终的商。
Python 版本
Python 版本的解题思路如下:
-
处理特殊情况,包括被除数等于 0,除数等于 1,以及避免溢出的情况(例如,被除数为-2^31,除数为-1)。
-
确定最终结果的符号(正数或负数),并将被除数和除数都转换为正数,以便进行位运算。
-
使用递归的二分搜索方法来找到商。递归函数的目标是找到一个整数 x,使得
(x + 1) * divisor > dividend且x * divisor ≤ dividend,或者(x + 1) * divisor ≥ dividend且x * divisor < dividend。这个 x 就是我们要找的商。 -
在递归的过程中,确保更新搜索的范围和值,同时处理可能的溢出情况。
-
最后,根据符号和边界情况返回最终的商。
Java 版本
Java 版本的解题思路如下:
-
处理特殊情况,包括被除数等于 0,除数等于 1,以及避免溢出的情况(例如,被除数为Integer.MIN_VALUE,除数为-1)。
-
确定最终结果的符号(正数或负数),并将被除数和除数都转换为正数,以便进行位运算。
-
使用递归的二分搜索方法来找到商。递归函数的目标是找到一个整数 x,使得
(x + 1) * divisor > dividend且x * divisor ≤ dividend,或者(x + 1) * divisor ≥ dividend且x * divisor < dividend。这个 x 就是我们要找的商。 -
在递归的过程中,确保更新搜索的范围和值,同时处理可能的溢出情况。
-
最后,根据符号和边界情况返回最终的商。
C++ 版本
C++ 版本的解题思路如下:
-
处理特殊情况,包括被除数等于 0,除数等于 1,以及避免溢出的情况(例如,被除数为INT_MIN,除数为-1)。
-
确定最终结果的符号(正数或负数),并将被除数和除数都转换为正数,以便进行位运算。
-
使用递归的二分搜索方法来找到商。递归函数的目标是找到一个整数 x,使得
(x + 1) * divisor > dividend且x * divisor ≤ dividend,或者(x + 1) * divisor ≥ dividend且x * divisor < dividend。这个 x 就是我们要找的商。 -
在递归的过程中,确保更新搜索的范围和值,同时处理可能的溢出情况。
-
最后,根据符号和边界情况返回最终的商。
总之,这些解决方案的核心思想都是使用二分搜索来找到商,同时处理特殊情况和溢出情况,以确保最终的计算结果正确。递归函数在实现中被广泛用于搜索过程。
代码
Go
func abs(x int) int {if x < 0 {return -x}return x
}// 解法一 递归版的二分搜索
func divide(dividend int, divisor int) int {sign, res := -1, 0// low, high := 0, abs(dividend)if dividend == 0 {return 0}if divisor == 1 {return dividend}if dividend == math.MinInt32 && divisor == -1 {return math.MaxInt32}if dividend > 0 && divisor > 0 || dividend < 0 && divisor < 0 {sign = 1}if dividend > math.MaxInt32 {dividend = math.MaxInt32}// 调用二分搜索函数计算商res = binarySearchQuotient(0, abs(dividend), abs(divisor), abs(dividend))// 处理溢出情况if res > math.MaxInt32 {return sign * math.MaxInt32}if res < math.MinInt32 {return sign * math.MinInt32}return sign * res
}// 二分搜索函数,用于计算商
func binarySearchQuotient(low, high, val, dividend int) int {quotient := low + (high-low)>>1if ((quotient+1)*val > dividend && quotient*val <= dividend) || ((quotient+1)*val >= dividend && quotient*val < dividend) {if (quotient+1)*val == dividend {return quotient + 1}return quotient}if (quotient+1)*val > dividend && quotient*val > dividend {return binarySearchQuotient(low, quotient-1, val, dividend)}if (quotient+1)*val < dividend && quotient*val < dividend {return binarySearchQuotient(quotient+1, high, val, dividend)}return 0
}func abs(x int) int {if x < 0 {return -x}return x
}// 解法二 非递归版的二分搜索
func divide(dividend int, divisor int) int {if dividend == math.MinInt32 && divisor == -1 {return math.MaxInt32}result := 0sign := -1if dividend > 0 && divisor > 0 || dividend < 0 && divisor < 0 {sign = 1}dividendAbs, divisorAbs := abs(dividend), abs(divisor)for dividendAbs >= divisorAbs {temp := divisorAbsmultiplier := 1for temp<<1 <= dividendAbs {temp <<= 1multiplier <<= 1}dividendAbs -= tempresult += multiplier}return sign * result
}
Python
class Solution:def divide(self, dividend: int, divisor: int) -> int:# 递归版def recursive_divide(dividend, divisor):if dividend < divisor:return 0quotient = 1div = divisorwhile (div + div) <= dividend:div += divquotient += quotientreturn quotient + recursive_divide(dividend - div, divisor)if dividend == 0:return 0if dividend == -2 ** 31 and divisor == -1:return 2 ** 31 - 1sign = 1 if (dividend > 0) == (divisor > 0) else -1dividend, divisor = abs(dividend), abs(divisor)result = recursive_divide(dividend, divisor)return sign * resultclass Solution:# 非递归版def divide(self, dividend: int, divisor: int) -> int:if dividend == 0:return 0if dividend == -2 ** 31 and divisor == -1:return 2 ** 31 - 1sign = 1 if (dividend > 0) == (divisor > 0) else -1dividend, divisor = abs(dividend), abs(divisor)result = 0while dividend >= divisor:temp, m = divisor, 1while dividend >= (temp << 1):temp <<= 1m <<= 1dividend -= tempresult += mreturn sign * result
Java
class Solution {public int divide(int dividend, int divisor) {// 递归版if (dividend == 0) {return 0;}if (dividend == Integer.MIN_VALUE && divisor == -1) {return Integer.MAX_VALUE;}int sign = (dividend > 0) == (divisor > 0) ? 1 : -1;long dvd = Math.abs((long) dividend);long dvs = Math.abs((long) divisor);int result = recursiveDivide(dvd, dvs);return sign * result;}private int recursiveDivide(long dividend, long divisor) {if (dividend < divisor) {return 0;}int quotient = 1;long div = divisor;while ((div + div) <= dividend) {div += div;quotient += quotient;}return quotient + recursiveDivide(dividend - div, divisor);}}
class Solution {// 非递归版public int divide(int dividend, int divisor) {if (dividend == 0) {return 0;}if (dividend == Integer.MIN_VALUE && divisor == -1) {return Integer.MAX_VALUE;}int sign = (dividend > 0) == (divisor > 0) ? 1 : -1;long dvd = Math.abs((long) dividend);long dvs = Math.abs((long) divisor);int result = 0;while (dvd >= dvs) {long temp = dvs;int m = 1;while (dvd >= (temp << 1)) {temp <<= 1;m <<= 1;}dvd -= temp;result += m;}return sign * result;}
}
Cpp
class Solution {
public:int divide(int dividend, int divisor) {// 处理特殊情况if (dividend == 0) {return 0;}if (divisor == 1) {return dividend;}if (dividend == INT_MIN && divisor == -1) {return INT_MAX;}int sign = (dividend > 0 && divisor > 0) || (dividend < 0 && divisor < 0) ? 1 : -1;// 处理溢出情况if (dividend > INT_MAX) {dividend = INT_MAX;}return sign * binarySearchQuotient(0, abs((long)dividend), abs((long)divisor), abs((long)dividend));}private:int binarySearchQuotient(long low, long high, long val, long dividend) {long quotient = low + (high - low) / 2;if (((quotient + 1) * val > dividend && quotient * val <= dividend) || ((quotient + 1) * val >= dividend && quotient * val < dividend)) {if ((quotient + 1) * val == dividend) {return quotient + 1;}return quotient;}if ((quotient + 1) * val > dividend && quotient * val > dividend) {return binarySearchQuotient(low, quotient - 1, val, dividend);}if ((quotient + 1) * val < dividend && quotient * val < dividend) {return binarySearchQuotient(quotient + 1, high, val, dividend);}return 0;}
};class Solution {
public:int divide(int dividend, int divisor) {// 处理特殊情况if (dividend == INT_MIN && divisor == -1) {return INT_MAX;}int result = 0;int sign = (dividend > 0 && divisor > 0) || (dividend < 0 && divisor < 0) ? 1 : -1;long dvd = abs((long)dividend);long dvs = abs((long)divisor);while (dvd >= dvs) {long temp = dvs;long m = 1;while (temp << 1 <= dvd) {temp <<= 1;m <<= 1;}dvd -= temp;// 处理溢出情况if (result > INT_MAX - m) {return sign == 1 ? INT_MAX : INT_MIN;}result += m;}return sign * result;}
};当讨论每个版本的解决方案时,我将分开介绍所需的详细基础知识。
Go 版本
-
Go 语言基础: 在理解 Go 版本的解决方案之前,您需要熟悉 Go 语言的基础知识,包括变量、函数、条件语句、循环等。
-
递归: Go 版本的解决方案中使用了递归来实现二分搜索,因此需要了解递归的概念和用法。
-
位运算: Go 版本中使用位运算来处理细节,如符号、边界情况等。因此,您需要了解 Go 中的位运算操作符(如
<<、>>)和位运算的基本原理。 -
边界情况处理: 了解如何处理边界情况是解决这个问题的关键之一,因为输入和输出受到了限制。需要考虑最小和最大的 32 位有符号整数。
Python 版本
-
Python 语言基础: 您需要熟悉 Python 语言的基础知识,包括变量、函数、条件语句、循环以及整数溢出处理。
-
递归: Python 版本中的递归解决方案使用了递归函数来实现二分搜索。您需要了解如何编写递归函数以及递归的工作原理。
-
位运算: 位运算在 Python 版本中也被用于处理符号和边界情况。了解 Python 中的位运算操作符(如
<<、>>)和位运算的基本原理将有助于理解解决方案。
Java 版本
-
Java 语言基础: 在理解 Java 版本的解决方案之前,您需要熟悉 Java 语言的基础知识,包括类、方法、条件语句、循环以及整数溢出处理。
-
递归: Java 版本的解决方案使用了递归函数来实现二分搜索。您需要了解如何编写递归函数以及递归的工作原理。
-
位运算: 位运算在 Java 版本中用于处理符号和边界情况。了解 Java 中的位运算操作符(如
<<、>>)和位运算的基本原理将有助于理解解决方案。 -
整数溢出处理: Java 版本考虑了整数溢出情况,并采取了措施来防止溢出。您需要了解 Java 中整数溢出的特点以及如何处理它。
C++ 版本
-
C++ 语言基础: 在理解 C++ 版本的解决方案之前,您需要熟悉 C++ 语言的基础知识,包括类、函数、条件语句、循环以及整数溢出处理。
-
递归: C++ 版本的解决方案使用了递归函数来实现二分搜索。您需要了解如何编写递归函数以及递归的工作原理。
-
位运算: 位运算在 C++ 版本中用于处理符号和边界情况。了解 C++ 中的位运算操作符(如
<<、>>)和位运算的基本原理将有助于理解解决方案。 -
整数溢出处理: C++ 版本考虑了整数溢出情况,并采取了措施来防止溢出。您需要了解 C++ 中整数溢出的特点以及如何处理它。
总之,理解每个版本的解决方案需要对编程语言的基础知识、递归、位运算和整数溢出处理有一定的了解。此外,了解问题的特殊要求和边界情况也是解决这个问题的关键。
30. Substring with Concatenation of All Words
题目
You are given a string, s, and a list of words, words, that are all of the same length. Find all starting indices of
substring(s) in s that is a concatenation of each word in words exactly once and without any intervening characters.
Example 1:
Input:s = "barfoothefoobarman",words = ["foo","bar"]
Output: [0,9]
Explanation: Substrings starting at index 0 and 9 are "barfoor" and "foobar" respectively.
The output order does not matter, returning [9,0] is fine too.
Example 2:
Input:s = "wordgoodgoodgoodbestword",words = ["word","good","best","word"]
Output: []
题目大意
给定一个源字符串 s,再给一个字符串数组,要求在源字符串中找到由字符串数组各种组合组成的连续串的起始下标,如果存在多个,在结果中都需要输出。
解题思路
这一题看似很难,但是有 2 个限定条件也导致这题不是特别难。1. 字符串数组里面的字符串长度都是一样的。2.
要求字符串数组中的字符串都要连续连在一起的,前后顺序可以是任意排列组合。
解题思路,先将字符串数组里面的所有字符串都存到 map
中,并累计出现的次数。然后从源字符串从头开始扫,每次判断字符串数组里面的字符串时候全部都用完了(计数是否为 0)
,如果全部都用完了,并且长度正好是字符串数组任意排列组合的总长度,就记录下这个组合的起始下标。如果不符合,就继续考察源字符串的下一个字符,直到扫完整个源字符串。
下面我将分别介绍每个版本的解题思路:
Go 版本:
-
初始化变量:
- 获取输入字符串
s的长度ls,单词数组words的长度m,以及单词的长度n。 - 初始化一个空的整数切片
ans用于存储结果。
- 获取输入字符串
-
主循环:
- 从字符串
s的前 n 个字符开始,循环遍历起始位置。 - 创建一个映射
differ用于跟踪当前窗口内每个单词的出现次数。
- 从字符串
-
遍历单词列表
words:- 对于单词列表中的每个单词,在
differ中增加其出现次数。 - 如果出现次数增加后变为 0,从
differ中删除该单词。
- 对于单词列表中的每个单词,在
-
主循环:
- 从当前起始位置开始,每次移动一个单词的长度
n,检查子串是否包含所有单词。 - 如果不包含,继续移动窗口。
- 如果
differ中不包含任何单词,说明子串包含了所有单词,将当前起始位置添加到结果中。
- 从当前起始位置开始,每次移动一个单词的长度
-
返回结果:返回存储结果的切片
ans。
Python 版本:
-
初始化变量:
- 初始化一个空列表
ans用于存储结果。 - 计算单词的长度
word_len,单词数组的长度total_words,单词数组的元素计数word_count,以及输入字符串s的长度s_len。
- 初始化一个空列表
-
循环遍历单词的起始位置:
- 外层循环迭代单词的起始位置,从 0 到
word_len-1。 - 内部维护两个指针
left和j,以及一个计数器count和一个单词计数器current_count。
- 外层循环迭代单词的起始位置,从 0 到
-
遍历字符串
s:- 内部循环遍历字符串
s从当前起始位置开始,每次移动一个单词的长度word_len。 - 在内部循环中,检查当前子串是否是单词数组的一个有效组合。
- 如果是有效组合,将起始位置
left添加到结果列表中。
- 内部循环遍历字符串
-
返回结果:返回存储结果的列表
ans。
Java 版本:
-
初始化变量:
- 初始化一个空列表
res用于存储结果。 - 创建一个映射
map用于存储单词以及它们的出现次数。 - 获取单词数组的长度
m。
- 初始化一个空列表
-
循环遍历可能的单词起始位置:
- 外层循环迭代单词的起始位置,从 0 到
len(words[0])-1。
- 外层循环迭代单词的起始位置,从 0 到
-
遍历字符串
s:- 内部循环遍历字符串
s,从当前起始位置开始,每次移动一个单词的长度。 - 在内部循环中,检查当前子串是否是单词数组的一个有效组合。
- 如果是有效组合,将起始位置添加到结果列表
res中。
- 内部循环遍历字符串
-
返回结果:返回存储结果的列表
res。
C++ 版本:
-
初始化变量:
- 初始化一个空向量
ans用于存储结果。 - 获取单词数组的长度
m和单词的长度wordsize。 - 创建一个映射
mp用于存储单词以及它们的出现次数。 - 获取输入字符串
s的长度n。
- 初始化一个空向量
-
循环遍历可能的单词起始位置:
- 外层循环迭代单词的起始位置,从 0 到
wordsize-1。
- 外层循环迭代单词的起始位置,从 0 到
-
遍历字符串
s:- 内部循环遍历字符串
s,从当前起始位置开始,每次移动一个单词的长度。 - 在内部循环中,检查当前子串是否是单词数组的一个有效组合。
- 如果是有效组合,将起始位置添加到结果向量
ans中。
- 内部循环遍历字符串
-
返回结果:返回存储结果的向量
ans。
这些是每个版本的基本解题思路。它们都采用了滑动窗口技巧,从不同的起始位置开始,逐步移动窗口并检查子串是否满足条件。同时,它们还利用了数据结构(如映射或计数器)来统计单词的出现次数以进行比较。不同的编程语言在实现细节上有所不同,但整体思路是一致的。
代码
Go
func findSubstring(s string, words []string) (ans []int) {// 获取输入字符串 `s` 的长度ls, m, n := len(s), len(words), len(words[0])// 遍历字符串 `s` 的前 n 个字符for i := 0; i < n && i+m*n <= ls; i++ {// 使用 map `differ` 来跟踪子串中每个单词的出现次数differ := map[string]int{}// 遍历单词列表 `words`for j := 0; j < m; j++ {// 将子串中的每个单词加入到 `differ` 中,并统计出现次数differ[s[i+j*n:i+(j+1)*n]]++}// 遍历单词列表 `words`for _, word := range words {// 减少 `differ` 中对应单词的出现次数differ[word]--// 如果出现次数减少到 0,从 `differ` 中删除这个单词if differ[word] == 0 {delete(differ, word)}}// 从当前位置 `i` 开始,每次移动一个单词长度 `n`,检查子串是否包含所有单词for start := i; start < ls-m*n+1; start += n {if start != i {// 更新 `differ`,增加新单词的出现次数,减少旧单词的出现次数word := s[start+(m-1)*n : start+m*n]differ[word]++if differ[word] == 0 {delete(differ, word)}word = s[start-n : start]differ[word]--if differ[word] == 0 {delete(differ, word)}}// 如果 `differ` 中不包含任何单词,说明子串包含了所有单词if len(differ) == 0 {ans = append(ans, start)}}}return
}Python
from collections import Counterclass Solution:def findSubstring(self, s: str, words: List[str]) -> List[int]:if not s or not words:return []ans = []word_len = len(words[0])total_words = len(words)word_count = Counter(words)s_len = len(s)for i in range(word_len):left = icount = 0current_count = Counter()for j in range(i, s_len - word_len + 1, word_len):word = s[j:j + word_len]if word in word_count:current_count[word] += 1count += 1while current_count[word] > word_count[word]:left_word = s[left:left + word_len]current_count[left_word] -= 1count -= 1left += word_lenif count == total_words:ans.append(left)else:current_count.clear()count = 0left = j + word_lenreturn ansJava
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;public class Solution {public List<Integer> findSubstring(String s, String[] words) {Map<String, Integer> map = new HashMap<>();// 将单词数组中的单词以及它们的出现次数存储在 map 中for (String str : words) {map.put(str, map.getOrDefault(str, 0) + 1);}int len = words[0].length(); // 单词的长度List<Integer> res = new ArrayList<>(); // 存储结果的列表// 遍历字符串 s 中每个可能的起始位置for (int i = 0; i < len; i++) {Map<String, Integer> newmap = new HashMap<>(); // 存储当前窗口内的单词出现次数int count = 0; // 记录窗口内匹配的单词数量for (int j = i; j <= s.length() - len;) {String cur = s.substring(j, j + len); // 当前窗口内的单词// 如果当前单词在单词数组中且未超出其出现次数限制if (map.containsKey(cur) && (!newmap.containsKey(cur) || newmap.get(cur) < map.get(cur))) {newmap.put(cur, newmap.getOrDefault(cur, 0) + 1); // 更新窗口内单词出现次数count++; // 增加匹配的单词数量// 如果窗口内匹配的单词数量等于单词数组的长度,表示找到一个满足条件的子串if (count == words.length) {res.add(j - len * (words.length - 1)); // 记录子串的起始位置count--;String pre = s.substring(j - len * (words.length - 1), j - len * (words.length - 2));newmap.put(pre, newmap.get(pre) - 1); // 更新窗口内单词出现次数}j += len; // 移动窗口} // 如果当前单词不在单词数组中else if (!map.containsKey(cur)) {count = 0;newmap.clear(); // 清空窗口内的单词记录j += len;} // 如果当前单词在单词数组中但超出其出现次数限制else {String pre = s.substring(j - len * count, j - len * (count - 1));newmap.put(pre, newmap.get(pre) - 1); // 更新窗口内单词出现次数count--; // 减少匹配的单词数量}}}return res; // 返回结果列表}
}Cpp
class Solution {
public:vector<int> findSubstring(string s, vector<string>& words) {const int n = s.length(); // 输入字符串的长度const int m = words.size(); // 单词数组的大小const int wordsize = words.front().length(); // 单词的长度unordered_map<string, int> mp; // 用于存储单词以及它们的出现次数for (auto &word : words)mp[word]++;vector<int> ans; // 存储结果的向量for (int i = 0; i < wordsize; ++i) { // 对于每个可能的起始位置unordered_map<string, int> cnt; // 用于存储当前窗口内的单词出现次数int start = i; // 记录符合条件的字符串的起始位置for (int j = i; j < n; j += wordsize) { // 遍历字符串 s 中所有单词string word = s.substr(j, wordsize);if (!mp.count(word)) { // 如果遇到不在单词数组中的单词,直接清空前面所有的计数cnt.clear();start = j + wordsize;} else {cnt[word] += 1;while (cnt[word] > mp[word]) { // 某个单词的计数超过了在单词数组中的出现次数,从左边减cnt[s.substr(start, wordsize)]--;start += wordsize;}if (j - start == (m - 1) * wordsize) // 如果窗口内匹配的单词数量等于单词数组的长度,表示找到一个满足条件的子串ans.push_back(start);}}}return ans;}
};每个版本的代码中所需要掌握的基础知识。
Go 版本:
-
Go 语言基础:
- 了解 Go 语言的基本语法,包括变量、循环、条件语句、函数等。
-
字符串处理:
- 了解如何使用字符串切片和字符串拼接操作来处理字符串。
- 理解字符串长度的计算方法。
-
映射(map):
- 了解 Go 中的映射数据结构,即
map,以及如何向映射中添加、删除和检索元素。 - 熟悉如何使用映射来实现单词计数和比较。
- 了解 Go 中的映射数据结构,即
-
循环和条件语句:
- 了解如何使用
for循环和if条件语句来实现迭代和条件判断。
- 了解如何使用
-
切片操作:
- 了解如何使用切片来操作数组或字符串的子集。
- 理解如何通过切片进行迭代。
Python 版本:
-
Python 语言基础:
- 熟悉 Python 语言的基本语法,包括变量、循环、条件语句、函数等。
-
字符串处理:
- 了解如何使用字符串切片和字符串拼接操作来处理字符串。
- 知道如何获取字符串的长度。
-
Counter 类:
- 了解 Python 中的
collections.Counter类,用于统计元素出现的次数。 - 知道如何使用
Counter对象来进行单词计数。
- 了解 Python 中的
-
循环和条件语句:
- 理解如何使用
for循环和if条件语句来实现迭代和条件判断。
- 理解如何使用
-
列表(List):
- 熟悉 Python 中的列表数据结构,以及如何使用列表来存储和操作数据。
Java 版本:
-
Java 语言基础:
- 熟悉 Java 语言的基本语法,包括变量、循环、条件语句、函数等。
-
字符串处理:
- 了解如何使用字符串切片和字符串拼接操作来处理字符串。
- 知道如何获取字符串的长度。
-
Map(映射):
- 理解 Java 中的
java.util.Map接口,以及如何使用HashMap实现映射。 - 知道如何向映射中添加、删除和检索元素。
- 理解 Java 中的
-
循环和条件语句:
- 了解如何使用
for循环和if条件语句来实现迭代和条件判断。
- 了解如何使用
-
列表(List):
- 熟悉 Java 中的列表数据结构,即
java.util.List,以及如何使用列表来存储和操作数据。
- 熟悉 Java 中的列表数据结构,即
C++ 版本:
-
C++ 语言基础:
- 理解 C++ 语言的基本语法,包括变量、循环、条件语句、函数等。
-
字符串处理:
- 了解如何使用字符串切片和字符串拼接操作来处理字符串。
- 知道如何获取字符串的长度。
-
STL(标准模板库):
- 理解 C++ STL 中的
std::unordered_map,用于实现映射。 - 知道如何向映射中添加、删除和检索元素。
- 理解 C++ STL 中的
-
循环和条件语句:
- 了解如何使用
for循环和if条件语句来实现迭代和条件判断。
- 了解如何使用
-
向量(Vector):
- 熟悉 C++ 中的向量数据结构,即
std::vector,以及如何使用向量来存储和操作数据。
- 熟悉 C++ 中的向量数据结构,即
这些是理解和编写提供的不同语言版本的代码所需的基本知识。每个版本都使用了相似的算法和数据结构,但具体的语法和库函数可能会有所不同。
31. Next Permutation
题目
Implementnext permutation, which rearranges numbers into the lexicographically next greater permutation of numbers.
If such an arrangement is not possible, it must rearrange it as the lowest possible order (i.e., sorted in ascending
order).
The replacement must be**in place**and use only constant extra
memory.
Example 1:
Input: nums = [1,2,3]
Output: [1,3,2]
Example 2:
Input: nums = [3,2,1]
Output: [1,2,3]
Example 3:
Input: nums = [1,1,5]
Output: [1,5,1]
Example 4:
Input: nums = [1]
Output: [1]
Constraints:
1 <= nums.length <= 1000 <= nums[i] <= 100
题目大意
实现获取 下一个排列 的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。必须
原地 修改,只允许使用额外常数空间。
解题思路
Go 版本解题思路:
-
寻找下一个排列:首先,我们要找到下一个排列,即重新排列给定数字序列,使其成为字典序中的下一个更大的排列。
-
寻找较小数的位置:从右往左遍历整数切片
nums,寻找第一个满足nums[i] < nums[i+1]的下标i。这个位置代表了较小数的位置。 -
寻找较大数的位置:如果找到了
i,则在下降区间[i+1, n)中从右往左找到第一个满足nums[i] < nums[j]的下标j,这个位置代表了较大数的位置。 -
交换较小数和较大数:交换
nums[i]和nums[j],这一步完成后,区间[i+1, n)一定是一个降序区间。 -
翻转子数组:对
[i+1, n)区间内的元素进行原地翻转,使其变为升序,这样才能生成下一个排列。
Python 版本解题思路:
Python 版本的解题思路与 Go 版本相似,只是使用了 Python 的列表和对象。
-
寻找下一个排列:与 Go 版本相同,我们首先要找到下一个排列,即重新排列给定数字序列,使其成为字典序中的下一个更大的排列。
-
寻找较小数的位置:从右往左遍历整数列表
nums,寻找第一个满足nums[i] < nums[i+1]的下标i,代表了较小数的位置。 -
寻找较大数的位置:如果找到了
i,则在下降区间[i+1, n)中从右往左找到第一个满足nums[i] < nums[j]的下标j,代表了较大数的位置。 -
交换较小数和较大数:交换
nums[i]和nums[j],这一步完成后,区间[i+1, n)一定是一个降序区间。 -
翻转子数组:对
[i+1, n)区间内的元素进行原地翻转,使其变为升序,这样才能生成下一个排列。
Java 版本解题思路:
Java 版本的解题思路与 Go 和 Python 版本相似,只是使用了 Java 的数组和类。
-
寻找下一个排列:与其他版本相同,首先要找到下一个排列,即重新排列给定数字序列,使其成为字典序中的下一个更大的排列。
-
寻找较小数的位置:从右往左遍历整数数组
nums,寻找第一个满足nums[i] < nums[i+1]的下标i,代表了较小数的位置。 -
寻找较大数的位置:如果找到了
i,则在下降区间[i+1, n)中从右往左找到第一个满足nums[i] < nums[j]的下标j,代表了较大数的位置。 -
交换较小数和较大数:交换
nums[i]和nums[j],这一步完成后,区间[i+1, n)一定是一个降序区间。 -
翻转子数组:对
[i+1, n)区间内的元素进行原地翻转,使其变为升序,这样才能生成下一个排列。
C++ 版本解题思路:
C++ 版本的解题思路与 Go、Python 和 Java 版本相似,只是使用了 C++ 的数组和类。
-
寻找下一个排列:与其他版本相同,首先要找到下一个排列,即重新排列给定数字序列,使其成为字典序中的下一个更大的排列。
-
寻找较小数的位置:从右往左遍历整数数组
nums,寻找第一个满足nums[i] < nums[i+1]的下标i,代表了较小数的位置。 -
寻找较大数的位置:如果找到了
i,则在下降区间[i+1, n)中从右往左找到第一个满足nums[i] < nums[j]的下标j,代表了较大数的位置。 -
交换较小数和较大数:交换
nums[i]和nums[j],这一步完成后,区间[i+1, n)一定是一个降序区间。 -
翻转子数组:对
[i+1, n)区间内的元素进行原地翻转,使其变为升序,这样才能生成下一个排列。
代码
Go
// 解法一
// 定义一个函数 nextPermutation,用于生成下一个排列
func nextPermutation(nums []int) {// 定义两个变量 i 和 j,并初始化为 0i, j := 0, 0// 从倒数第二个元素开始向前遍历整数切片 nums,寻找第一个满足 nums[i] < nums[i+1] 的 ifor i = len(nums) - 2; i >= 0; i-- {if nums[i] < nums[i+1] {break}}// 如果找到了 i,表示存在下一个排列if i >= 0 {// 从最后一个元素开始向前遍历整数切片 nums,寻找第一个满足 nums[j] > nums[i] 的 jfor j = len(nums) - 1; j > i; j-- {if nums[j] > nums[i] {break}}// 交换 nums[i] 和 nums[j]swap(&nums, i, j)}// 对从 i+1 到末尾的部分进行翻转,以获得下一个排列reverse(&nums, i+1, len(nums)-1)
}// 定义一个函数 reverse,用于翻转整数切片 nums 中从位置 i 到 j 的元素
func reverse(nums *[]int, i, j int) {// 使用双指针将元素从两端向中间逐个交换for i < j {swap(nums, i, j)i++j--}
}// 定义一个函数 swap,用于交换整数切片 nums 中位置 i 和 j 的元素
func swap(nums *[]int, i, j int) {// 使用指针访问和交换切片中的元素值(*nums)[i], (*nums)[j] = (*nums)[j], (*nums)[i]
}Python
class Solution:def nextPermutation(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""# Step 1: Find the first decreasing element from right to left (i)i = len(nums) - 2while i >= 0 and nums[i] >= nums[i + 1]:i -= 1# Step 2: Find the first element larger than nums[i] from right to left (j)if i >= 0:j = len(nums) - 1while j > i and nums[j] <= nums[i]:j -= 1# Step 3: Swap nums[i] and nums[j]nums[i], nums[j] = nums[j], nums[i]# Step 4: Reverse the subarray to the right of ileft, right = i + 1, len(nums) - 1while left < right:nums[left], nums[right] = nums[right], nums[left]left += 1right -= 1Java
class Solution {public void nextPermutation(int[] nums) {// Step 1: Find the first decreasing element from right to left (i)int i = nums.length - 2;while (i >= 0 && nums[i] >= nums[i + 1]) {i--;}// Step 2: Find the first element larger than nums[i] from right to left (j)if (i >= 0) {int j = nums.length - 1;while (j > i && nums[j] <= nums[i]) {j--;}// Step 3: Swap nums[i] and nums[j]int temp = nums[i];nums[i] = nums[j];nums[j] = temp;}// Step 4: Reverse the subarray to the right of iint left = i + 1, right = nums.length - 1;while (left < right) {int temp = nums[left];nums[left] = nums[right];nums[right] = temp;left++;right--;}}
}Cpp
class Solution {
public:void nextPermutation(vector<int>& nums) {// Step 1: Find the first decreasing element from right to left (i)int i = nums.size() - 2;while (i >= 0 && nums[i] >= nums[i + 1]) {i--;}// Step 2: Find the first element larger than nums[i] from right to left (j)if (i >= 0) {int j = nums.size() - 1;while (j > i && nums[j] <= nums[i]) {j--;}// Step 3: Swap nums[i] and nums[j]swap(nums[i], nums[j]);}// Step 4: Reverse the subarray to the right of iint left = i + 1, right = nums.size() - 1;while (left < right) {swap(nums[left], nums[right]);left++;right--;}}
};基础知识
Go 版本:
-
Go 语言基础: 了解 Go 语言的基本语法、数据类型、函数定义和使用、切片(slice)等相关知识。
-
指针: 了解指针的概念以及如何在 Go 中使用指针。
-
函数: 理解如何定义和调用函数,以及函数的参数和返回值。
-
数组切片: 了解 Go 中的切片概念和切片操作,包括切片的创建和修改。
Python 版本:
-
Python 基础: 了解 Python 的基本语法、列表(list)、条件语句和循环。
-
类和对象: 理解如何定义类和创建对象(在 Python 类中定义方法)。
-
列表操作: 了解如何操作列表,包括索引、切片、迭代和修改列表元素。
Java 版本:
-
Java 基础: 熟悉 Java 的基本语法、数组、循环和条件语句。
-
类和方法: 了解如何定义类和方法,并且如何在类中使用成员变量和方法。
-
数组操作: 熟悉 Java 中数组的创建、遍历和修改操作。
C++ 版本:
-
C++ 基础: 了解 C++ 的基本语法、数组、循环和条件语句。
-
函数: 理解如何定义和调用函数,以及函数的参数和返回值。
-
数组操作: 了解如何操作数组,包括索引、遍历和修改数组元素。
32. Longest Valid Parentheses
题目
Given a string containing just the characters'('and')', find the length of the longest valid (well-formed)
parentheses substring.
Example 1:
Input: s = "(()"
Output: 2
Explanation: The longest valid parentheses substring is "()".
Example 2:
Input: s = ")()())"
Output: 4
Explanation: The longest valid parentheses substring is "()()".
Example 3:
Input: s = ""
Output: 0
Constraints:
0 <= s.length <= 3 * 104s[i]is'(', or')'.
题目大意
给你一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
解题思路
以下是每个版本的解题思路的详细介绍:
Go 版本解题思路:
Go 版本的解题思路是利用栈来处理括号匹配问题,并采用了双指针的方法来计算最长有效括号子串的长度。主要步骤如下:
-
定义一个辅助函数
max(a, b int) int用于返回两个整数中的较大值。 -
初始化
left、right和maxLength变量,它们分别用于记录左括号数量、右括号数量和最长有效括号子串的长度,初始值都为 0。 -
遍历输入字符串
s,从左到右:- 如果当前字符是 ‘(’, 则增加
left计数器。 - 如果当前字符是 ‘)’, 则增加
right计数器。 - 如果
left和right计数器相等,说明找到了一个有效的括号子串,计算当前有效括号子串的长度,并更新maxLength。 - 如果
right大于left,则重置left和right计数器为 0,因为当前的括号串无法匹配。
- 如果当前字符是 ‘(’, 则增加
-
重置
left、right和maxLength变量为 0,再进行一次从右到左的遍历,处理右括号数量多于左括号数量的情况。 -
返回
maxLength,它表示最长有效括号子串的长度。
Python 版本解题思路:
Python 版本的解题思路与 Go 版本相似,也是利用栈来处理括号匹配问题,并采用了双指针的方法来计算最长有效括号子串的长度。主要步骤如下:
-
定义一个辅助函数
max(a, b)用于返回两个数中的较大值。 -
初始化
left、right和maxLength变量,它们分别用于记录左括号数量、右括号数量和最长有效括号子串的长度,初始值都为 0。 -
遍历输入字符串
s,从左到右:- 如果当前字符是 ‘(’, 则增加
left计数器。 - 如果当前字符是 ‘)’, 则增加
right计数器。 - 如果
left和right计数器相等,说明找到了一个有效的括号子串,计算当前有效括号子串的长度,并更新maxLength。 - 如果
right大于left,则重置left和right计数器为 0,因为当前的括号串无法匹配。
- 如果当前字符是 ‘(’, 则增加
-
重置
left、right和maxLength变量为 0,再进行一次从右到左的遍历,处理右括号数量多于左括号数量的情况。 -
返回
maxLength,它表示最长有效括号子串的长度。
Java 版本解题思路:
Java 版本的解题思路与 Go 和 Python 版本相似,也是利用栈来处理括号匹配问题,并采用了双指针的方法来计算最长有效括号子串的长度。主要步骤如下:
-
初始化
left、right和maxLength变量,它们分别用于记录左括号数量、右括号数量和最长有效括号子串的长度,初始值都为 0。 -
遍历输入字符串
s,从左到右:- 如果当前字符是 ‘(’, 则增加
left计数器。 - 如果当前字符是 ‘)’, 则增加
right计数器。 - 如果
left和right计数器相等,说明找到了一个有效的括号子串,计算当前有效括号子串的长度,并更新maxLength。 - 如果
right大于left,则重置left和right计数器为 0,因为当前的括号串无法匹配。
- 如果当前字符是 ‘(’, 则增加
-
重置
left、right和maxLength变量为 0,再进行一次从右到左的遍历,处理右括号数量多于左括号数量的情况。 -
返回
maxLength,它表示最长有效括号子串的长度。
C++ 版本解题思路:
C++ 版本的解题思路与 Go、Python 和 Java 版本相似,也是利用栈来处理括号匹配问题,并采用了双指针的方法来计算最长有效括号子串的长度。主要步骤如下:
-
初始化
left、right和maxLength变量,它们分别用于记录左括号数量、右括号数量和最长有效括号子串的长度,初始值都为 0。 -
遍历输入字符串
s,从左到右:- 如果当前字符是 ‘(’, 则增加
left计数器。 - 如果当前字符是 ‘)’, 则增加
right计数器。 - 如果
left和right计数器相等,说明找到了一个有效的括号子串,计算当前有效括号子串的长度,并更新maxLength。 - 如果
right大于left,则重置left和right计数器为 0,因为当前的括号串无法匹配。
- 如果当前字符是 ‘(’, 则增加
-
重置
left、right和maxLength变量为 0,再进行一次从右到左的遍历,处理右括号数量多于左括号数量的情况。 -
返回
maxLength,它表示最长有效括号子串的长度。
代码
Go
func max(a, b int) int {// 返回两个整数中的较大值if a > b {return a}return b
}// 解法二 双指针
func longestValidParentheses(s string) int {// 初始化左右指针和最大有效括号子串长度left, right, maxLength := 0, 0, 0for i := 0; i < len(s); i++ {// 如果当前字符是左括号 '(',增加左括号计数if s[i] == '(' {left++} else {// 如果当前字符是右括号 ')',增加右括号计数right++}// 如果左右括号计数相等,说明找到了一个有效的括号子串if left == right {// 计算当前有效括号子串的长度并更新最大长度maxLength = max(maxLength, 2*right)} else if right > left {// 如果右括号计数大于左括号计数,重置左右指针left, right = 0, 0}}// 重置左右指针left, right = 0, 0for i := len(s) - 1; i >= 0; i-- {// 从右向左遍历字符串,处理与上面相同的逻辑if s[i] == '(' {left++} else {right++}if left == right {maxLength = max(maxLength, 2*left)} else if left > right {left, right = 0, 0}}// 返回最大有效括号子串的长度return maxLength
}Python
class Solution:def longestValidParentheses(self, s: str) -> int:def max(a, b):return a if a > b else bleft, right, maxLength = 0, 0, 0# 从左向右遍历字符串for char in s:if char == '(':left += 1else:right += 1if left == right:maxLength = max(maxLength, 2 * right)elif right > left:left, right = 0, 0left, right = 0, 0# 从右向左遍历字符串for i in range(len(s) - 1, -1, -1):char = s[i]if char == '(':left += 1else:right += 1if left == right:maxLength = max(maxLength, 2 * left)elif left > right:left, right = 0, 0return maxLengthJava
class Solution {public int longestValidParentheses(String s) {int left = 0, right = 0, maxLength = 0;// 从左向右遍历字符串for (char c : s.toCharArray()) {if (c == '(') {left++;} else {right++;}if (left == right) {maxLength = Math.max(maxLength, 2 * right);} else if (right > left) {left = 0;right = 0;}}left = 0;right = 0;// 从右向左遍历字符串for (int i = s.length() - 1; i >= 0; i--) {char c = s.charAt(i);if (c == '(') {left++;} else {right++;}if (left == right) {maxLength = Math.max(maxLength, 2 * left);} else if (left > right) {left = 0;right = 0;}}return maxLength;}
}Cpp
class Solution {
public:int longestValidParentheses(string s) {int left = 0, right = 0, maxLength = 0;// 从左向右遍历字符串for (char c : s) {if (c == '(') {left++;} else {right++;}if (left == right) {maxLength = max(maxLength, 2 * right);} else if (right > left) {left = 0;right = 0;}}left = 0;right = 0;// 从右向左遍历字符串for (int i = s.length() - 1; i >= 0; i--) {char c = s[i];if (c == '(') {left++;} else {right++;}if (left == right) {maxLength = max(maxLength, 2 * left);} else if (left > right) {left = 0;right = 0;}}return maxLength;}
};Go 版本:
-
Go 语言基础:
- 变量声明和初始化
- 循环(for 循环)
- 条件语句(if-else)
- 函数声明和调用
- 数组和切片(slices)的基本操作
-
栈的概念:
- Go 中可以使用切片(slices)来模拟栈的行为
Python 版本:
-
Python 语言基础:
- 变量声明和初始化
- 循环(for 循环)
- 条件语句(if-else)
- 函数声明和调用
- 字符串的基本操作
-
栈的概念:
- Python 中可以使用列表(list)来模拟栈的行为
Java 版本:
-
Java 语言基础:
- 类和对象的概念
- 方法声明和调用
- 循环(for 循环)
- 条件语句(if-else)
- 字符串的基本操作
-
栈的概念:
- Java 中可以使用集合类(如 ArrayList 或 LinkedList)来模拟栈的行为
C++ 版本:
-
C++ 语言基础:
- 变量声明和初始化
- 函数声明和调用
- 循环(for 循环)
- 条件语句(if-else)
- 字符串的基本操作
-
栈的概念:
- C++ 中可以使用标准库中的容器(如 std::vector 或 std::deque)来模拟栈的行为
33. Search in Rotated Sorted Array
题目
Suppose an array sorted in ascending order is rotated at some pivot unknown to you beforehand.
(i.e., [0,1,2,4,5,6,7] might become [4,5,6,7,0,1,2]).
You are given a target value to search. If found in the array return its index, otherwise return -1.
You may assume no duplicate exists in the array.
Your algorithm’s runtime complexity must be in the order of O(log n).
Example 1:
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Example 2:
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
题目大意
假设按照升序排序的数组在预先未知的某个点上进行了旋转。( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
解题思路
下面将分别介绍每个版本的解题思路:
Go 版本解题思路:
- 初始化两个指针
low和high,分别指向数组的开头和结尾。 - 使用二分查找的循环来搜索目标值。
- 在每次迭代中,计算中间元素的索引
mid。 - 检查中间元素与目标值的关系:
- 如果中间元素等于目标值,则直接返回中间元素的索引。
- 如果中间元素大于最左边的元素(说明左半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素小于等于最右边的元素(说明右半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素与最左边的元素相等,说明可能存在重复元素,可以将最左边的指针
low向右移动一位。 - 如果中间元素与最右边的元素相等,说明可能存在重复元素,可以将最右边的指针
high向左移动一位。
- 重复步骤 3 和步骤 4,直到
low大于high,此时未找到目标值,返回 -1。
Python 版本解题思路:
- 初始化两个指针
low和high,分别指向数组的开头和结尾。 - 使用二分查找的循环来搜索目标值。
- 在每次迭代中,计算中间元素的索引
mid。 - 检查中间元素与目标值的关系:
- 如果中间元素等于目标值,则直接返回中间元素的索引。
- 如果中间元素大于最左边的元素(说明左半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素小于等于最右边的元素(说明右半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素与最左边的元素相等,说明可能存在重复元素,可以将最左边的指针
low向右移动一位。 - 如果中间元素与最右边的元素相等,说明可能存在重复元素,可以将最右边的指针
high向左移动一位。
- 重复步骤 3 和步骤 4,直到
low大于high,此时未找到目标值,返回 -1。
Java 版本解题思路:
- 初始化两个指针
low和high,分别指向数组的开头和结尾。 - 使用二分查找的循环来搜索目标值。
- 在每次迭代中,计算中间元素的索引
mid。 - 检查中间元素与目标值的关系:
- 如果中间元素等于目标值,则直接返回中间元素的索引。
- 如果中间元素大于最左边的元素(说明左半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素小于等于最右边的元素(说明右半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素与最左边的元素相等,说明可能存在重复元素,可以将最左边的指针
low向右移动一位。 - 如果中间元素与最右边的元素相等,说明可能存在重复元素,可以将最右边的指针
high向左移动一位。
- 重复步骤 3 和步骤 4,直到
low大于high,此时未找到目标值,返回 -1。
C++ 版本解题思路:
- 初始化两个指针
low和high,分别指向数组的开头和结尾。 - 使用二分查找的循环来搜索目标值。
- 在每次迭代中,计算中间元素的索引
mid。 - 检查中间元素与目标值的关系:
- 如果中间元素等于目标值,则直接返回中间元素的索引。
- 如果中间元素大于最左边的元素(说明左半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素小于等于最右边的元素(说明右半段是有序的),则比较目标值与中间元素的大小关系:
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
low = mid + 1。 - 否则,目标值在左半段无序部分,更新
high = mid - 1。
- 如果目标值大于中间元素且小于等于最右边的元素,说明目标值在右半段有序部分,更新
- 如果中间元素与最左边的元素相等,说明可能存在重复元素,可以将最左边的指针
low向右移动一位。 - 如果中间元素与最右边的元素相等,说明可能存在重复元素,可以将最右边的指针
high向左移动一位。
- 重复步骤 3 和步骤 4,直到
low大于high,此时未找到目标值,返回 -1。
这四个版本的解题思路基本一致,都是使用二分查找的变种来在旋转有序数组中搜索目标值,关键是正确处理不同情况下指针的更新以及边界条件的处理。算法的时间复杂度是 O(log n),因为每次迭代都将搜索范围减半。不同版本的代码实现方式有所不同,但核心逻辑相似。
代码
Go
func search(nums []int, target int) int {// 检查数组是否为空,如果是空数组则直接返回-1if len(nums) == 0 {return -1}// 初始化两个指针,分别指向数组的开头和结尾low, high := 0, len(nums)-1// 使用二分查找的循环来搜索目标值for low <= high {// 计算中间元素的索引mid := low + (high-low)>>1// 如果中间元素等于目标值,则直接返回中间元素的索引if nums[mid] == target {return mid} else if nums[mid] > nums[low] { // 如果中间元素在数值大的一部分区间里// 检查目标值是否在左半部分区间内,如果是则更新高指针if nums[low] <= target && target < nums[mid] {high = mid - 1} else {// 否则更新低指针low = mid + 1}} else if nums[mid] < nums[high] { // 如果中间元素在数值小的一部分区间里// 检查目标值是否在右半部分区间内,如果是则更新低指针if nums[mid] < target && target <= nums[high] {low = mid + 1} else {// 否则更新高指针high = mid - 1}} else {// 处理中间元素等于边界元素的情况,移动边界指针以去除重复元素if nums[low] == nums[mid] {low++}if nums[high] == nums[mid] {high--}}}// 如果未找到目标值,则返回-1return -1
}Python
class Solution:def search(self, nums, target: int):# 如果数组为空,直接返回-1if len(nums) == 0:return -1# 如果数组只有一个元素,分两种情况判断elif len(nums) == 1:if nums[0] != target:return -1else:return 0# 找到旋转点的位置for i in range(len(nums) - 1):if nums[i] > nums[i + 1]:flag = i + 1break# 在旋转点左边进行二分查找left = self.binary_search(nums, target, 0, flag - 1)if left != -1:return leftelse:# 如果左边没有找到,就在旋转点右边进行二分查找right = self.binary_search(nums, target, flag, len(nums) - 1)if right == -1:return -1else:return rightdef binary_search(self, nums, target, left, right):l, r = left, rightwhile l <= r:mid = l + (r - l) // 2if nums[mid] == target:return midelif nums[mid] < target:l = mid + 1else:r = mid - 1return -1Java
class Solution {public int search(int[] nums, int target) {if (nums == null || nums.length == 0) {return -1;}int low = 0, high = nums.length - 1;while (low <= high) {int mid = low + (high - low) / 2;if (nums[mid] == target) {return mid;} else if (nums[mid] > nums[low]) {if (nums[low] <= target && target < nums[mid]) {high = mid - 1;} else {low = mid + 1;}} else if (nums[mid] < nums[high]) {if (nums[mid] < target && target <= nums[high]) {low = mid + 1;} else {high = mid - 1;}} else {if (nums[low] == nums[mid]) {low++;}if (nums[high] == nums[mid]) {high--;}}}return -1;}
}Cpp
class Solution {
public:int search(vector<int>& nums, int target) {if (nums.empty()) {return -1;}int low = 0, high = nums.size() - 1;while (low <= high) {int mid = low + (high - low) / 2;if (nums[mid] == target) {return mid;} else if (nums[mid] > nums[low]) {if (nums[low] <= target && target < nums[mid]) {high = mid - 1;} else {low = mid + 1;}} else if (nums[mid] < nums[high]) {if (nums[mid] < target && target <= nums[high]) {low = mid + 1;} else {high = mid - 1;}} else {if (nums[low] == nums[mid]) {low++;}if (nums[high] == nums[mid]) {high--;}}}return -1;}
};当用不同编程语言实现算法时,需要掌握以下基础知识:
Go 版本:
-
函数定义与调用:了解如何定义和调用函数,包括函数的参数和返回值。
-
数组与切片:Go 中没有传统的数组,而是使用切片来处理动态数组。需要了解如何声明、初始化和操作切片。
-
循环与条件语句:了解如何使用
for和if语句来实现循环和条件判断。 -
二分查找:理解二分查找的原理和实现方法,包括如何计算中间元素的索引和更新指针。
-
算法复杂度:理解算法复杂度的概念,包括时间复杂度和空间复杂度,并了解如何分析算法的性能。
Python 版本:
-
类和方法:了解如何定义类和类方法,并如何创建类的实例。
-
列表:Python 中的列表类似于动态数组,需要了解如何声明、初始化和操作列表。
-
循环与条件语句:了解如何使用
for和if语句来实现循环和条件判断。 -
二分查找:理解二分查找的原理和实现方法,包括如何计算中间元素的索引和更新指针。
-
函数递归:理解函数递归的概念,以及如何在递归中解决问题。
Java 版本:
-
类和方法:了解如何定义类和类方法,并如何创建类的实例。
-
数组:Java 中有静态数组,需要了解如何声明、初始化和操作数组。
-
循环与条件语句:了解如何使用
for和if语句来实现循环和条件判断。 -
二分查找:理解二分查找的原理和实现方法,包括如何计算中间元素的索引和更新指针。
-
算法复杂度:理解算法复杂度的概念,包括时间复杂度和空间复杂度,并了解如何分析算法的性能。
C++ 版本:
-
类和方法:了解如何定义类和类方法,并如何创建类的实例。
-
向量:C++ 中的向量类似于动态数组,需要了解如何声明、初始化和操作向量。
-
循环与条件语句:了解如何使用
for和if语句来实现循环和条件判断。 -
二分查找:理解二分查找的原理和实现方法,包括如何计算中间元素的索引和更新指针。
-
算法复杂度:理解算法复杂度的概念,包括时间复杂度和空间复杂度,并了解如何分析算法的性能。
以上是实现搜索旋转排序数组算法所需要掌握的基础知识,包括语言特性、数据结构操作、循环和条件判断、二分查找算法和算法复杂度分析等方面的知识。不同编程语言有不同的语法和库函数,但核心的算法思想和逻辑都是相似的。
34. Find First and Last Position of Element in Sorted Array
题目
Given an array of integers nums sorted in ascending order, find the starting and ending position of a given target value.
Your algorithm’s runtime complexity must be in the order of O(log n).
If the target is not found in the array, return [-1, -1].
Example 1:
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]
Example 2:
Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]
题目大意
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。你的算法时间复杂度必须是 O(log n) 级别。如果数组中不存在目标值,返回 [-1, -1]。
解题思路
Go 版本的解题思路:
-
首先,初始化两个指针
l_ptr和r_ptr,它们分别指向数组的起始位置和结束位置。 -
初始化一个整数切片
ans,用于存储目标值的范围,初始值为[-1, -1]。 -
使用二分搜索的思想,在循环中不断缩小搜索范围,直到找到目标值的范围或确定目标值不存在。
-
在每次迭代中,计算中间位置的索引
mid。 -
如果中间位置的元素等于目标值,则更新
ans[0]和ans[1]为mid。然后,通过循环向左和向右扩展,找到目标值的第一个和最后一个位置。 -
如果中间位置的元素大于目标值,则将右指针
r_ptr移动到mid - 1,以缩小搜索范围到左半部分。 -
如果中间位置的元素小于目标值,则将左指针
l_ptr移动到mid + 1,以缩小搜索范围到右半部分。 -
最终,返回包含目标值范围的
ans数组。
Python 版本的解题思路:
Python 版本的解题思路与 Go 版本类似,但使用了函数和模块的结构来组织代码:
-
首先,定义了两个辅助函数
find_left和find_right,它们分别用于查找目标值的左边界和右边界。 -
在主函数
searchRange中,初始化两个整数,用于存储目标值的左边界和右边界。这些值是通过调用辅助函数来找到的。 -
辅助函数
find_left和find_right采用二分搜索的思想,不断缩小搜索范围,直到找到目标值的边界或确定目标值不存在。 -
当找到左边界时,继续向右搜索,找到右边界。
-
最终,返回包含目标值范围的结果列表。
Java 版本的解题思路:
Java 版本的解题思路与 Go 版本类似,但使用了类和方法的结构来组织代码:
-
在
Solution类中,定义了一个方法searchRange来解决问题。 -
在
searchRange方法中,初始化两个整数,用于存储目标值的左边界和右边界。 -
使用
while循环,在循环中不断缩小搜索范围,直到找到目标值的范围或确定目标值不存在。 -
在每次迭代中,计算中间位置的索引
mid。 -
如果中间位置的元素等于目标值,则更新左边界和右边界,然后通过循环向左和向右扩展,找到目标值的第一个和最后一个位置。
-
如果中间位置的元素大于目标值,则缩小搜索范围到左半部分,将右指针
r_ptr移动到mid - 1。 -
如果中间位置的元素小于目标值,则缩小搜索范围到右半部分,将左指针
l_ptr移动到mid + 1。 -
最终,返回包含目标值范围的整数数组。
C++ 版本的解题思路:
C++ 版本的解题思路与 Java 版本类似,但使用了类和方法的结构来组织代码:
-
在
Solution类中,定义了一个方法searchRange来解决问题。 -
在
searchRange方法中,初始化两个整数,用于存储目标值的左边界和右边界。 -
使用
while循环,在循环中不断缩小搜索范围,直到找到目标值的范围或确定目标值不存在。 -
在每次迭代中,计算中间位置的索引
mid。 -
如果中间位置的元素等于目标值,则更新左边界和右边界,然后通过循环向左和向右扩展,找到目标值的第一个和最后一个位置。
-
如果中间位置的元素大于目标值,则缩小搜索范围到左半部分,将右指针
r_ptr移动到mid - 1。 -
如果中间位置的元素小于目标值,则缩小搜索范围到右半部分,将左指针
l_ptr移动到mid。 -
最终,返回包含目标值范围的整数数组。
这些是每个版本的解题思路的详细说明,希望这能帮助您更好地理解每个解决方案的工作原理。如果您有任何进一步的问题,请随时提问。
代码
Go
func searchRange(nums []int, target int) []int {// 获取数组的长度n := len(nums)// 初始化左指针为 0l_prt := 0// 初始化右指针为数组长度减一r_prt := n - 1// 初始化答案数组,用于存储目标值的范围ans := []int{-1, -1} // 在左指针小于等于右指针的条件下进行循环for l_prt <= r_prt {// 计算中间位置的索引mid := ((r_prt - l_prt) >> 1) + l_prt// 如果中间位置的元素等于目标值if nums[mid] == target {// 更新答案的左边界和右边界为中间位置ans[0] = midans[1] = mid// 从中间位置向左扩展,找到目标值的第一个位置for ans[0] > 0 && nums[ans[0]-1] == target {ans[0]--}// 从中间位置向右扩展,找到目标值的最后一个位置for ans[1] < n - 1 && nums[ans[1] + 1] == target {ans[1]++}// 跳出循环,因为已经找到了目标值的范围break} else if nums[mid] > target {// 如果中间位置的元素大于目标值,缩小搜索范围到左半部分r_prt = mid - 1} else {// 如果中间位置的元素小于目标值,缩小搜索范围到右半部分l_prt = mid + 1}}// 返回包含目标值范围的答案数组return ans
}Python
class Solution:def searchRange(self, nums: List[int], target: int) -> List[int]:# 辅助函数:查找目标值的左边界def find_left():start, end = 0, len(nums) - 1res = -1 # 初始化结果为-1,表示未找到while start <= end:mid = (start + end) // 2 # 计算中间位置的索引if nums[mid] < target:start = mid + 1 # 如果中间值小于目标值,缩小搜索范围到右半部分elif nums[mid] > target:end = mid - 1 # 如果中间值大于目标值,缩小搜索范围到左半部分else:res = mid # 找到目标值,更新结果为当前位置end = mid - 1 # 继续向左搜索更左边的位置return res# 辅助函数:查找目标值的右边界def find_right():start, end = 0, len(nums) - 1res = -1 # 初始化结果为-1,表示未找到while start <= end:mid = (start + end) // 2 # 计算中间位置的索引if nums[mid] < target:start = mid + 1 # 如果中间值小于目标值,缩小搜索范围到右半部分elif nums[mid] > target:end = mid - 1 # 如果中间值大于目标值,缩小搜索范围到左半部分else:res = mid # 找到目标值,更新结果为当前位置start = mid + 1 # 继续向右搜索更右边的位置return res# 返回包含目标值范围的结果数组,左边界和右边界分别由辅助函数找到return [find_left(), find_right()]Java
class Solution {public int[] searchRange(int[] nums, int target) {// 获取数组的长度int n = nums.length;// 初始化左指针为0int l_ptr = 0;// 初始化右指针为数组长度减一int r_ptr = n - 1;// 初始化答案数组,用于存储目标值的范围int[] ans = {-1, -1};// 在左指针小于等于右指针的条件下进行循环while (l_ptr <= r_ptr) {// 计算中间位置的索引int mid = (r_ptr - l_ptr) / 2 + l_ptr;// 如果中间位置的元素等于目标值if (nums[mid] == target) {// 更新答案的左边界和右边界为中间位置ans[0] = mid;ans[1] = mid;// 从中间位置向左扩展,找到目标值的第一个位置while (ans[0] > 0 && nums[ans[0] - 1] == target) {ans[0]--;}// 从中间位置向右扩展,找到目标值的最后一个位置while (ans[1] < n - 1 && nums[ans[1] + 1] == target) {ans[1]++;}// 跳出循环,因为已经找到了目标值的范围break;} else if (nums[mid] > target) {// 如果中间位置的元素大于目标值,缩小搜索范围到左半部分r_ptr = mid - 1;} else {// 如果中间位置的元素小于目标值,缩小搜索范围到右半部分l_ptr = mid + 1;}}// 返回包含目标值范围的答案数组return ans;}
}Cpp
class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int ret; // 用于存储目标值的起始位置int l = 0, r = nums.size() - 1; // 初始化左右指针,表示搜索范围// 第一个循环:查找目标值的起始位置while (l < r) {int mid = (l + r) / 2; // 计算中间位置的索引if (nums[mid] < target) {l = mid + 1; // 如果中间值小于目标值,缩小搜索范围到右半部分} else {r = mid; // 否则,缩小搜索范围到左半部分}}// 如果找到的位置超出数组范围或者该位置的值不等于目标值,返回{-1, -1}if (l == nums.size() || nums[l] != target) {return {-1, -1};}ret = l; // 记录目标值的起始位置l = 0;r = nums.size() - 1;// 第二个循环:查找目标值的结束位置while (l < r) {int mid = (l + r + 1) / 2; // 计算中间位置的索引if (nums[mid] > target) {r = mid - 1; // 如果中间值大于目标值,缩小搜索范围到左半部分} else {l = mid; // 否则,缩小搜索范围到右半部分}}// 返回包含目标值范围的结果数组,包括起始位置和结束位置return {ret, l};}
};每个版本的所需基础知识:
Go 版本的基础知识:
-
切片(Slices):Go 语言中的切片是动态数组,非常常用于处理数组数据。在这个解决方案中,
nums是一个整数切片,而ans也是一个整数切片,用于存储目标值的范围。 -
循环和条件语句:解决方案中使用了
for循环和if条件语句来实现逻辑控制,例如,在二分搜索中不断缩小搜索范围。 -
二分搜索:这个问题的关键是使用二分搜索算法。需要了解二分搜索的基本原理,即通过比较中间元素与目标值的大小,将搜索范围缩小一半,直到找到目标或确定目标不存在。
Python 版本的基础知识:
-
列表(Lists):Python 中的列表类似于数组,用于存储一组元素。在这个解决方案中,
nums是一个整数列表,而ans也是一个整数列表,用于存储目标值的范围。 -
函数和模块:解决方案中定义了两个辅助函数
find_left和find_right,并使用了函数来组织代码。还需要了解 Python 模块的概念,例如List类型在typing模块中的导入。 -
循环和条件语句:与 Go 版本一样,Python 版本也使用了
for循环和if条件语句来实现逻辑控制。 -
二分搜索:同样需要了解二分搜索的基本原理和实现方式。
Java 版本的基础知识:
-
数组:Java 使用数组来存储一组元素。在这个解决方案中,
nums是一个整数数组,而ans也是一个整数数组,用于存储目标值的范围。 -
类和方法:Java 版本使用了一个类
Solution,其中包含一个方法searchRange来解决问题。需要了解如何定义类和方法,并调用它们。 -
循环和条件语句:与其他版本一样,Java 版本也使用了
while循环和if条件语句来实现逻辑控制。 -
二分搜索:了解二分搜索的基本原理和实现方式。
C++ 版本的基础知识:
-
向量(Vectors):C++ 中的向量类似于动态数组,用于存储一组元素。在这个解决方案中,
nums是一个整数向量,而ans也是一个整数向量,用于存储目标值的范围。 -
类和方法:与 Java 版本一样,C++ 版本也使用了一个类
Solution,其中包含一个方法searchRange来解决问题。需要了解如何定义类和方法,并调用它们。 -
循环和条件语句:与其他版本一样,C++ 版本也使用了
while循环和if条件语句来实现逻辑控制。 -
二分搜索:了解二分搜索的基本原理和实现方式。
35. Search Insert Position
题目
Given a sorted array and a target value, return the index if the target is found. If not, return the index where it
would be if it were inserted in order.
You may assume no duplicates in the array.
Example 1:
Input: [1,3,5,6], 5
Output: 2
Example 2:
Input: [1,3,5,6], 2
Output: 1
Example 3:
Input: [1,3,5,6], 7
Output: 4
Example 4:
Input: [1,3,5,6], 0
Output: 0
题目大意
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
解题思路
以下是每个版本的解题思路:
Go 版本解题思路:
-
定义两个指针
low和high,它们分别指向数组的起始位置和末尾位置。 -
使用循环执行二分查找:
- 计算中间元素的索引
mid,使用(low + (high - low) >> 1)计算。 - 如果中间元素
nums[mid]大于或等于目标值target,将high指针移动到mid - 1,表示在左半部分继续搜索。 - 否则,如果中间元素小于目标值
target:- 检查中间元素的下一个元素是否大于等于目标值
target或者是否已经到达数组末尾。 - 如果是,说明目标值应该插入到当前位置的后面,返回
mid + 1作为插入位置的索引。 - 否则,将
low指针移动到mid + 1,表示在右半部分继续搜索。
- 检查中间元素的下一个元素是否大于等于目标值
- 计算中间元素的索引
-
如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回 0。
Python 版本解题思路:
-
定义两个指针
low和high,它们分别指向数组的起始位置和末尾位置。 -
使用
while循环执行二分查找:- 计算中间元素的索引
mid,使用(low + (high - low) // 2)计算。 - 如果中间元素
nums[mid]大于或等于目标值target,将high指针移动到mid - 1,表示在左半部分继续搜索。 - 否则,如果中间元素小于目标值
target:- 检查中间元素的下一个元素是否大于等于目标值
target或者是否已经到达数组末尾。 - 如果是,说明目标值应该插入到当前位置的后面,返回
mid + 1作为插入位置的索引。 - 否则,将
low指针移动到mid + 1,表示在右半部分继续搜索。
- 检查中间元素的下一个元素是否大于等于目标值
- 计算中间元素的索引
-
如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回 0。
Java 版本解题思路:
-
定义两个指针
low和high,它们分别指向数组的起始位置和末尾位置。 -
使用
while循环执行二分查找:- 计算中间元素的索引
mid,使用(low + (high - low) / 2)计算。 - 如果中间元素
nums[mid]大于或等于目标值target,将high指针移动到mid - 1,表示在左半部分继续搜索。 - 否则,如果中间元素小于目标值
target:- 检查中间元素的下一个元素是否大于等于目标值
target或者是否已经到达数组末尾。 - 如果是,说明目标值应该插入到当前位置的后面,返回
mid + 1作为插入位置的索引。 - 否则,将
low指针移动到mid + 1,表示在右半部分继续搜索。
- 检查中间元素的下一个元素是否大于等于目标值
- 计算中间元素的索引
-
如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回 0。
C++ 版本解题思路:
-
定义两个指针
low和high,它们分别指向向量(动态数组)的起始位置和末尾位置。 -
使用
while循环执行二分查找:- 计算中间元素的索引
mid,使用(low + (high - low) / 2)计算。 - 如果中间元素
nums[mid]大于或等于目标值target,将high指针移动到mid - 1,表示在左半部分继续搜索。 - 否则,如果中间元素小于目标值
target:- 检查中间元素的下一个元素是否大于等于目标值
target或者是否已经到达向量末尾。 - 如果是,说明目标值应该插入到当前位置的后面,返回
mid + 1作为插入位置的索引。 - 否则,将
low指针移动到mid + 1,表示在右半部分继续搜索。
- 检查中间元素的下一个元素是否大于等于目标值
- 计算中间元素的索引
-
如果循环结束仍然没有找到合适的位置,说明目标值应该插入到向量的开头,返回 0。
总的来说,每个版本的解题思路都是基于二分查找算法的变种,通过不断更新 low 和 high 指针来逼近目标值的插入位置。根据不同的编程语言,语法和数据结构的细节会有所不同,但基本思路保持一致。
代码
Go
func searchInsert(nums []int, target int) int {// 定义两个指针,low 指向数组的起始位置,high 指向数组的末尾位置low, high := 0, len(nums)-1// 使用循环执行二分查找for low <= high {// 计算中间元素的索引mid := low + (high-low)>>1// 如果中间元素大于等于目标值if nums[mid] >= target {// 将 high 指针移动到中间元素的前一个位置high = mid - 1} else {// 如果中间元素小于目标值// 检查中间元素的下一个元素是否大于等于目标值,或者是否已经到达数组末尾if (mid == len(nums)-1) || (nums[mid+1] >= target) {// 如果是,说明目标值应该插入到当前位置的后面,返回当前位置的下一个索引return mid + 1}// 否则,将 low 指针移动到中间元素的下一个位置low = mid + 1}}// 如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回0return 0
}Python
class Solution:def searchInsert(self, nums: List[int], target: int) -> int:# 定义两个指针,low指向数组的起始位置,high指向数组的末尾位置low, high = 0, len(nums) - 1# 使用循环执行二分查找while low <= high:# 计算中间元素的索引mid = low + (high - low) // 2# 如果中间元素大于等于目标值if nums[mid] >= target:# 将high指针移动到中间元素的前一个位置high = mid - 1else:# 如果中间元素小于目标值# 检查中间元素的下一个元素是否大于等于目标值,或者是否已经到达数组末尾if mid == len(nums) - 1 or nums[mid + 1] >= target:# 如果是,说明目标值应该插入到当前位置的后面,返回当前位置的下一个索引return mid + 1# 否则,将low指针移动到中间元素的下一个位置low = mid + 1# 如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回0return 0Java
class Solution {public int searchInsert(int[] nums, int target) {// 定义两个指针,low指向数组的起始位置,high指向数组的末尾位置int low = 0, high = nums.length - 1;// 使用循环执行二分查找while (low <= high) {// 计算中间元素的索引int mid = low + (high - low) / 2;// 如果中间元素大于等于目标值if (nums[mid] >= target) {// 将high指针移动到中间元素的前一个位置high = mid - 1;} else {// 如果中间元素小于目标值// 检查中间元素的下一个元素是否大于等于目标值,或者是否已经到达数组末尾if (mid == nums.length - 1 || nums[mid + 1] >= target) {// 如果是,说明目标值应该插入到当前位置的后面,返回当前位置的下一个索引return mid + 1;}// 否则,将low指针移动到中间元素的下一个位置low = mid + 1;}}// 如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回0return 0;}
}Cpp
class Solution {
public:int searchInsert(vector<int>& nums, int target) {// 定义两个指针,low指向数组的起始位置,high指向数组的末尾位置int low = 0, high = nums.size() - 1;// 使用循环执行二分查找while (low <= high) {// 计算中间元素的索引int mid = low + (high - low) / 2;// 如果中间元素大于等于目标值if (nums[mid] >= target) {// 将high指针移动到中间元素的前一个位置high = mid - 1;} else {// 如果中间元素小于目标值// 检查中间元素的下一个元素是否大于等于目标值,或者是否已经到达数组末尾if (mid == nums.size() - 1 || nums[mid + 1] >= target) {// 如果是,说明目标值应该插入到当前位置的后面,返回当前位置的下一个索引return mid + 1;}// 否则,将low指针移动到中间元素的下一个位置low = mid + 1;}}// 如果循环结束仍然没有找到合适的位置,说明目标值应该插入到数组的开头,返回0return 0;}
};当理解和编写每个版本的代码时,你需要掌握以下基础知识:
- Go 版本:
- 切片 (Slices):Go 中的数组和切片是非常重要的数据结构。切片是动态数组,用于存储一系列相同类型的元素。
- 循环和条件语句:你需要了解 Go 中的
for循环和if条件语句的用法,以便编写代码中的循环和条件判断。 - 函数:你需要了解如何定义和调用函数,以及函数的参数和返回值。
- 二分查找算法:理解二分查找算法的工作原理对于理解此代码非常重要。
- Python 版本:
- 列表 (Lists):Python 中的列表是有序的数据结构,可以存储多种数据类型。在此问题中,列表用于存储整数元素。
- 循环和条件语句:你需要了解 Python 中的
while循环和if条件语句的使用方法,以便编写代码中的循环和条件判断。 - 类和方法:Python 中的
class和方法定义方式。在这个版本中,代码被封装在一个类中。 - 二分查找算法:理解二分查找算法的工作原理对于理解此代码非常重要。
- Java 版本:
- 数组:Java 中的数组是一种静态数据结构,你需要了解如何声明、初始化和访问数组元素。
- 循环和条件语句:你需要了解 Java 中的
while循环和if条件语句的使用方法,以便编写代码中的循环和条件判断。 - 类和方法:Java 中的类和方法的定义方式。在这个版本中,代码被封装在一个类中。
- 二分查找算法:理解二分查找算法的工作原理对于理解此代码非常重要。
- C++ 版本:
- 向量 (Vectors):C++ 中的向量是一种动态数组,类似于 Python 中的列表或 Go 中的切片。
- 循环和条件语句:你需要了解 C++ 中的
while循环和if条件语句的使用方法,以便编写代码中的循环和条件判断。 - 类和方法:C++ 中的类和方法的定义方式。在这个版本中,代码被封装在一个类中。
- 二分查找算法:理解二分查找算法的工作原理对于理解此代码非常重要。
总的来说,无论选择哪种编程语言的版本,都需要熟悉数组、循环、条件语句和二分查找算法。此外,了解特定编程语言的语法和标准库函数也是非常重要的,以便能够正确地编写和理解代码。如果你不熟悉某种特定语言,建议先学习该语言的基础知识,然后再尝试理解和编写相应版本的代码。
相关文章:

Go-Python-Java-C-LeetCode高分解法-第五周合集
前言 本题解Go语言部分基于 LeetCode-Go 其他部分基于本人实践学习 个人题解GitHub连接:LeetCode-Go-Python-Java-C Go-Python-Java-C-LeetCode高分解法-第一周合集 Go-Python-Java-C-LeetCode高分解法-第二周合集 Go-Python-Java-C-LeetCode高分解法-第三周合集 G…...
)
【前端知识】前端加密算法(base64、md5、sha1、escape/unescape、AES/DES)
前端加密算法 一、base64加解密算法 简介:Base64算法使用64个字符(A-Z、a-z、0-9、、/)来表示二进制数据的64种可能性,将每3个字节的数据编码为4个可打印字符。如果字节数不是3的倍数,将会进行填充。 优点࿱…...
leetcode 925. 长按键入
2023.9.7 我的基本思路是两数组字符逐一对比,遇到不同的字符,判断一下typed与上一字符是否相同,不相同返回false,相同则继续对比。 最后要分别判断name和typed分别先遍历完时的情况。直接看代码: class Solution { p…...

[CMake教程] 循环
目录 一、foreach()二、while()三、break() 与 continue() 作为一个编程语言,CMake也少不了循环流程控制,他提供两种循环foreach() 和 while()。 一、foreach() 基本语法: foreach(<loop_var> <items>)<commands> endfo…...
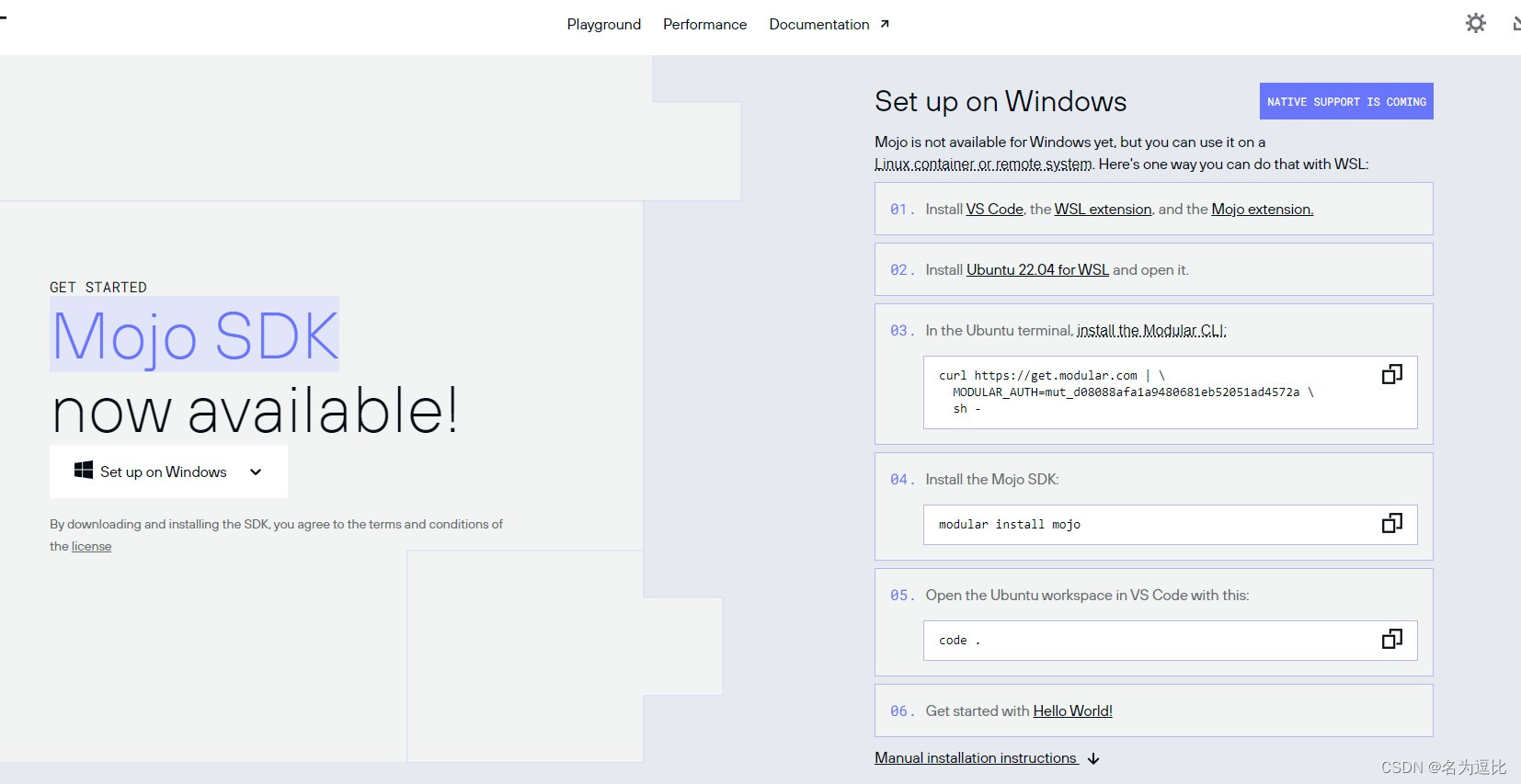
Mojo安装使用初体验
一个声称比python块68000倍的语言 蹭个热度,安装试试 系统配置要求: 不支持Windows系统 配置要求: 系统:Ubuntu 20.04/22.04 LTSCPU:x86-64 CPU (with SSE4.2 or newer)内存:8 GiB memoryPython 3.8 - 3.10g or cla…...

艺术与AI:科技与艺术的完美融合
文章目录 艺术创作的新工具生成艺术艺术与数据 AI与互动艺术虚拟现实(VR)与增强现实(AR)机器学习与互动性 艺术与AI的伦理问题结语 🎉欢迎来到AIGC人工智能专栏~艺术与AI:科技与艺术的完美融合 ☆* o(≧▽≦…...
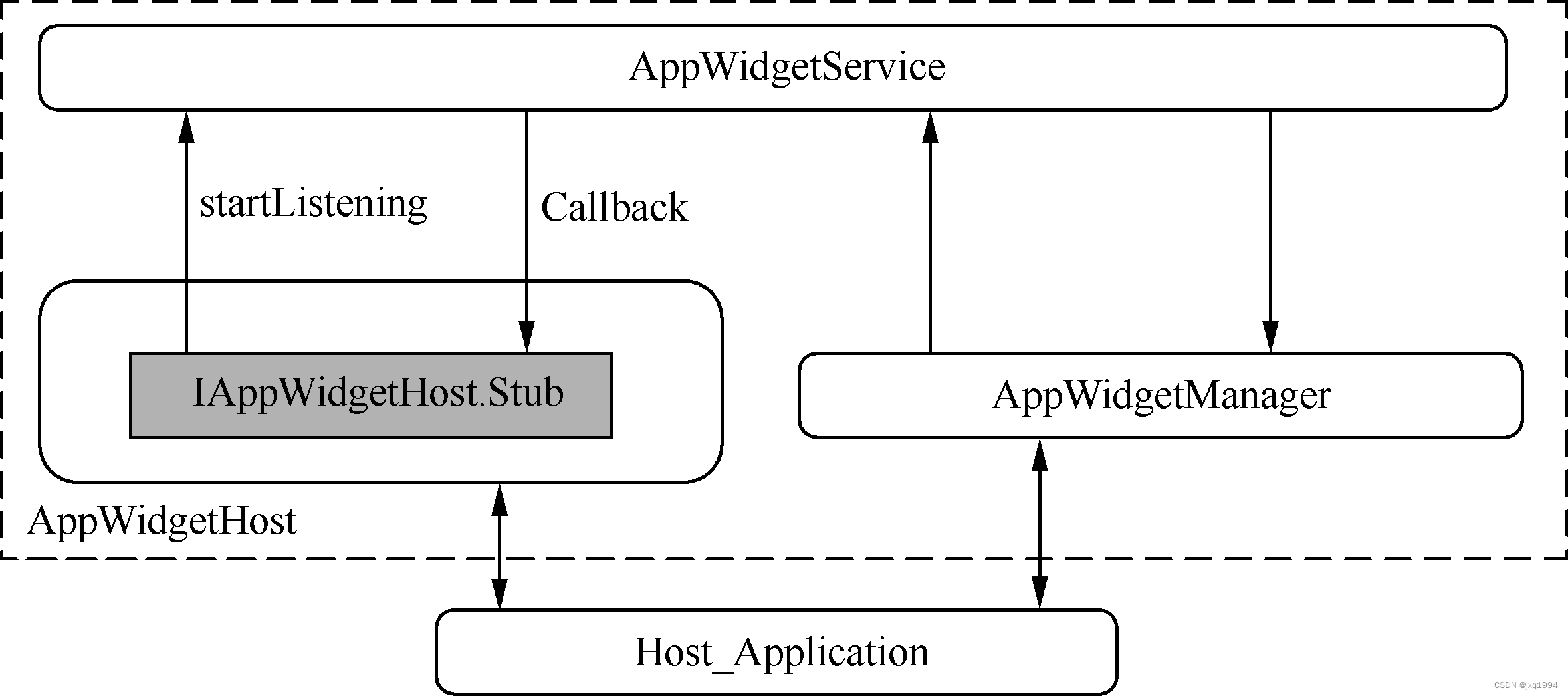
Android常用的工具“小插件”——Widget机制
Widget俗称“小插件”,是Android系统中一个很常用的工具。比如我们可以在Launcher中添加一个音乐播放器的Widget。 在Launcher上可以添加插件,那么是不是说只有Launcher才具备这个功能呢? Android系统并没有具体规定谁才能充当“Widget容器…...

探索在云原生环境中构建的大数据驱动的智能应用程序的成功案例,并分析它们的关键要素。
文章目录 1. Netflix - 个性化推荐引擎2. Uber - 实时数据分析和决策支持3. Airbnb - 价格预测和优化5. Google - 自然语言处理和搜索优化 🎈个人主页:程序员 小侯 🎐CSDN新晋作者 🎉欢迎 👍点赞✍评论⭐收藏 ✨收录专…...

jupyter 添加中文选项
文章目录 jupyter 添加中文选项1. 下载中文包2. 选择中文重新加载一下,页面就变成中文了 jupyter 添加中文选项 1. 下载中文包 pip install jupyterlab-language-pack-zh-CN2. 选择中文 重新加载一下,页面就变成中文了 这才是设置中文的正解ÿ…...

系列十、Java操作RocketMQ之批量消息
一、概述 RocketMQ可以一次性发送一组消息,那么这一组消息会被当做一个消息进行消费。 二、案例代码 2.1、pom 同系列五 2.2、RocketMQConstant 同系列五 2.3、BatchConsumer package org.star.batch.consumer;import cn.hutool.core.util.StrUtil; import lom…...

leetcode1两数之和
题目: 给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。 你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。 你…...

近年GDC服务器分享合集(四): 《火箭联盟》:为免费游玩而进行的扩展
如今,网络游戏采用免费游玩(Free to Play)加内购的比例要远大于买断制,这是因为前者能带来更低的用户门槛。甚至有游戏为了获取更多的用户,选择把原来的买断制改为免费游玩,一个典型的例子就是最近的网易的…...

android反射详解
1,反射的定义 一般情况下,我们使用某个类时必定知道它是什么类,是用来做什么的,并且能够获得此类的引用。于是我们直接对这个类进行实例化,之后使用这个类对象进行操作。 反射则是一开始并不知道我要初始化的类对象是…...

Python 反射和动态执行
反射主要应用于类的对象上,在运行时,将对象中的属性和方法反射出来,通过字符串对对象成员(属性、方法)进行查找、获取、删除、添加成员等动作,是一种基于字符串的事件驱动技术。 python是一门动态语言&…...

计算机网络常见端口号
端口号标识了一个主机上进行通信的不同的应用程序。比如网站服务器80端口一般都是开启的,等你来连接。 端口划分: (1)常用端口,公共端口(保留给公共服务所使用),端口号为0-1023之间…...
SpringBoot / Vue 对SSE的基本使用(简单上手)
一、SSE是什么? SSE技术是基于单工通信模式,只是单纯的客户端向服务端发送请求,服务端不会主动发送给客户端。服务端采取的策略是抓住这个请求不放,等数据更新的时候才返回给客户端,当客户端接收到消息后,…...
Qt串口基本设置与协议收发
前言 1.一直都想要做一个Qt上位机,趁着这个周末有时间,动手写一下 2.comboBox没有点击的信号,所以做了一个触发的功能 3.Qt的数据类型很奇怪,转来转去的我也搞得很迷糊 4.给自己挖个坑,下一期做一个查看波形的上位…...
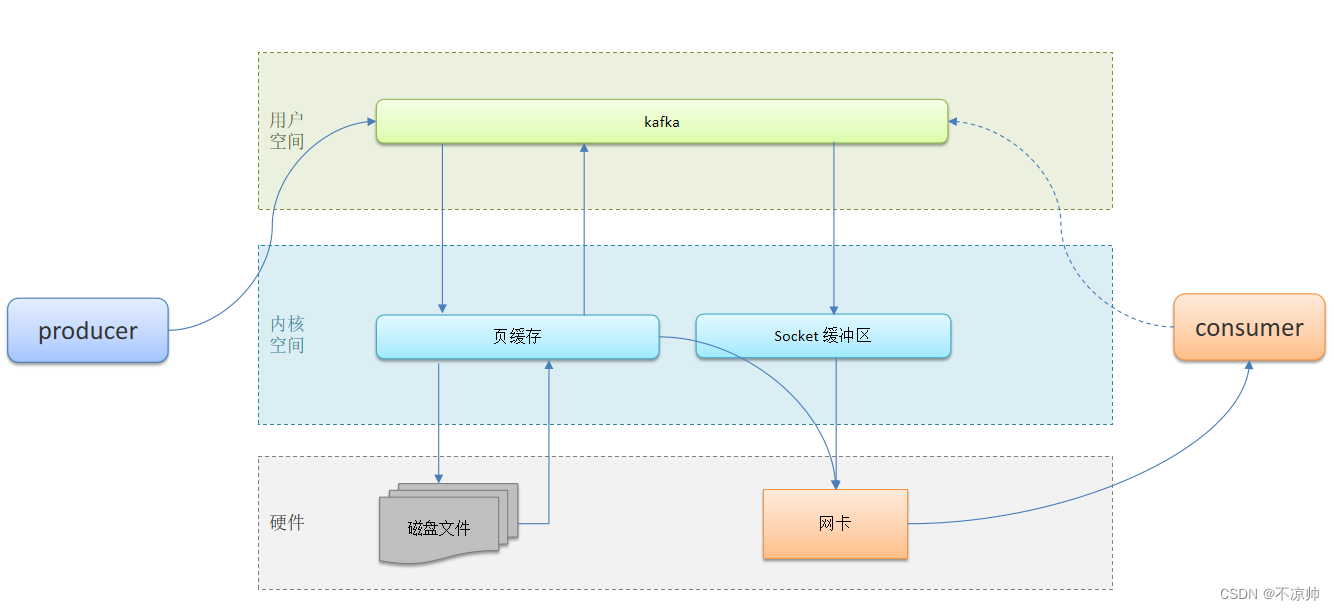
interview3-微服务与MQ
一、SpringCloud篇 (1)服务注册 常见的注册中心:eureka、nacos、zookeeper eureka做服务注册中心: 服务注册:服务提供者需要把自己的信息注册到eureka,由eureka来保存这些信息,比如服务名称、…...
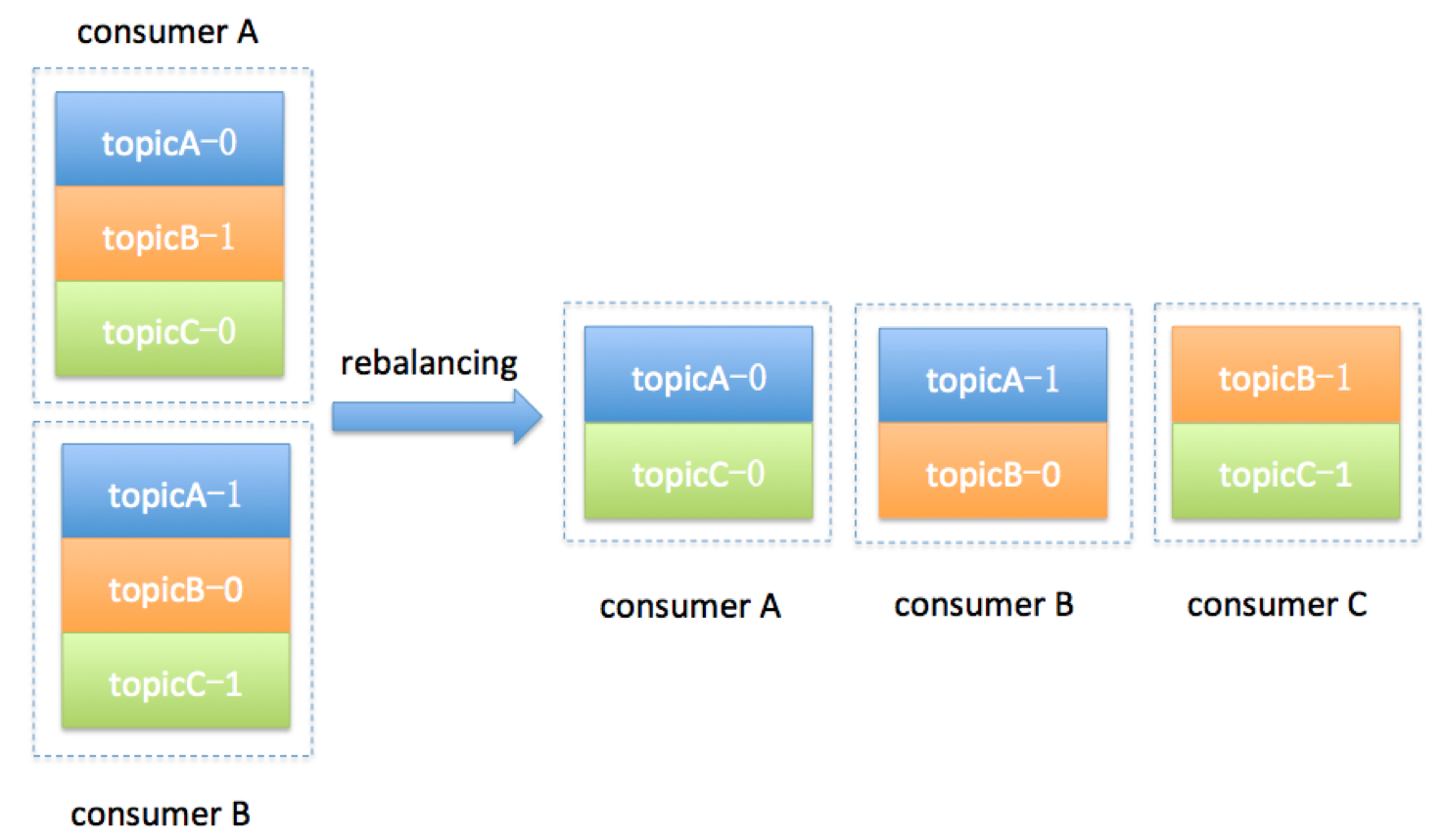
kafka详解一
kafka详解一 1、消息引擎背景 根据维基百科的定义,消息引擎系统是一组规范。企业利用这组规范在不同系统之间传递语义准确的消息,实现松耦合的异步式数据传递. 即:系统 A 发送消息给消息引擎系统,系统 B 从消息引擎系统中读取 A…...

Flutter yuv 转 rgb
1、引用yuv_converter库 yuv_converter: ^0.0.1 2、导入头文件: import package:yuv_converter/yuv_converter.dart;3、yuv转rgb YuvConverter.yuv420NV21ToRgba8888(yuvRawData, 512, 512) 根据yuv格式选择不同的api。 举个例子: void initState() …...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...
