第六章 图 五、图的深度优先遍历(DFS算法)
目录
一、定义
深度优先遍历通常用于解决以下问题:
深度优先遍历算法具有以下优点:
深度优先遍历算法的一个缺点是:
二、代码
空间复杂度:
时间复杂度:
邻接矩阵存储:
邻接表存储:
三、手动模拟深度优先遍历⭐⭐⭐⭐⭐
1、首先访问结点2
2、访问2的邻接点6
3、跳转到6,访问6的邻接结点,发现2已经被访问过了,于是访问7
4、跳转到7,访问7的邻接结点,6被访问过了所以跳过,访问8
5、跳转到8,访问8的邻接结点,访问4
6、继续访问跳转到4,访问4的邻接结点,访问3
7、跳转到3,访问3的邻接结点,访问6,6被访问过了(跳过),访问7(跳过),访问4(跳过),由于3的邻接结点都被访问完了,所以返回上一级;
8、遍历4,访问8(跳过),访问7(跳过),返回上一级;
9、上一级是8,所以遍历8,访问7(跳过),返回上一级;
10、遍历7,访问3(跳过),访问4(跳过),返回上一级;
11、遍历6,访问3(跳过),返回上一级;
12、遍历2,访问1;
13、跳转至1,访问2(跳过),访问5;
14、跳转至5,访问1,跳过;
至此,邻接表所有结点全部访问完毕。
四、深度优先生成树
五、深度优先生成森林
六、图的遍历与图的连通性
无向图:
有向图:
一、定义
1、深度优先遍历(Depth-First Search, DFS)是一种遍历或搜索图的算法。
2、该算法从图的某一个起始节点开始,递归地探索该节点的所有邻居节点,直到找出整个图的连通部分。
3、DFS使用了栈的数据结构来保存待访问的节点。
4、当访问一个节点时,我们将该节点入栈,并将其标记为已访问。
然后,如果该节点有未访问的邻居节点,我们就将邻居节点入栈并标记为已访问。
这个过程一直持续到栈为空为止。当栈为空时,我们就完成了整个图的深度优先遍历。
深度优先遍历通常用于解决以下问题:
- 检测一个无向图是否为连通图。
- 搜索一条路径,例如在迷宫中从起点到终点的最短路径。
- 找出一个无向图的所有连通分量。
深度优先遍历算法具有以下优点:
- 实现简单。
- 占用的空间相对较小,因为它只需要一个栈来保存待访问的节点。
- 适用于解决一些基于图的问题。
深度优先遍历算法的一个缺点是:
它可能会陷入无限循环中,因为它只是深度优先探索邻居节点,而不是考虑整个图的结构。这种缺点可以通过引入剪枝策略来解决,例如标记已访问的节点,或者设置搜索的深度限制。
二、代码
#include <iostream>
#include <vector>using namespace std;void DFS(int start, vector<vector<int>>& graph, vector<bool>& visited) {visited[start] = true; // 标记当前节点为已访问cout << start << " "; // 输出遍历到的节点for (int i = 0; i < graph[start].size(); i++) {int next = graph[start][i];if (!visited[next]) { // 如果下一个节点未被访问DFS(next, graph, visited); // 递归访问下一个节点}}
}int main() {// 构建一个图vector<vector<int>> graph = {{1, 2}, {0, 3, 4}, {0, 5, 6}, {1}, {1}, {2}, {2, 7}, {6}};vector<bool> visited(graph.size(), false); // 初始化所有节点为未访问状态DFS(0, graph, visited); // 从节点0开始深度优先遍历return 0;
}空间复杂度:
最好情况:
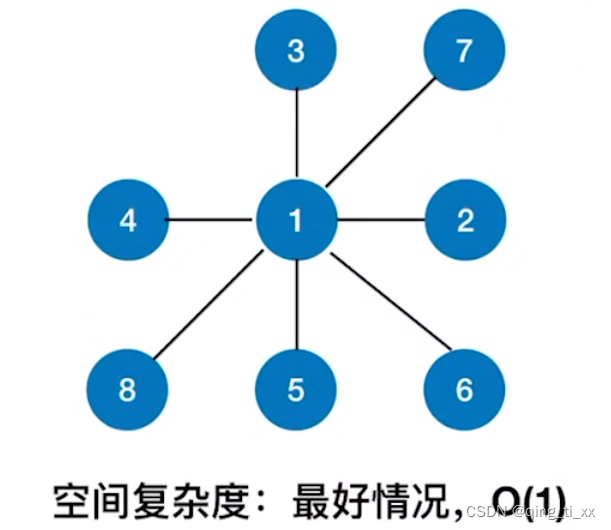
最坏情况:

时间复杂度:

邻接矩阵存储:
![]()
邻接表存储:
![]()
三、手动模拟深度优先遍历⭐⭐⭐⭐⭐
假如我们由如下邻接表:
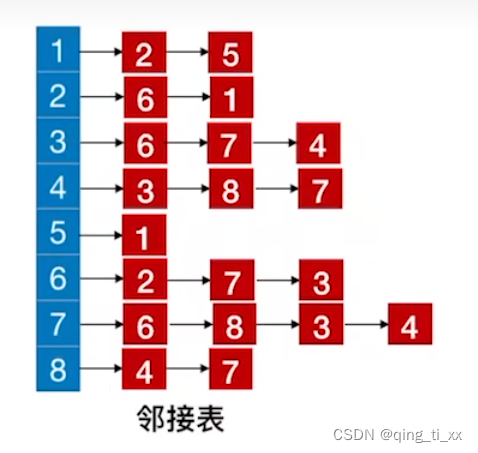
我们要得到从2开始的深度优先遍历序列。
1、首先访问结点2
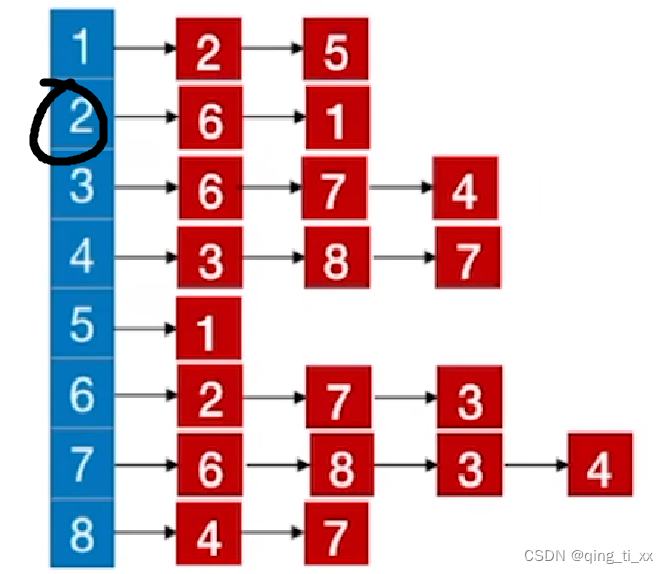
此时,遍历序列为

2、访问2的邻接点6
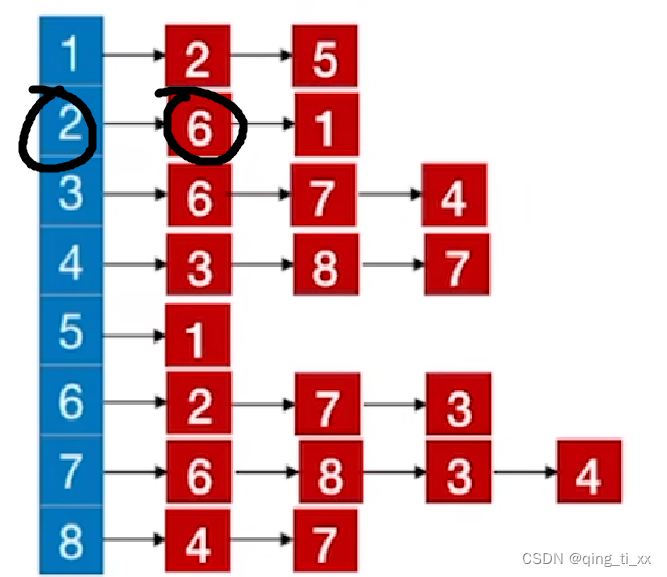
此时,遍历序列为

3、跳转到6,访问6的邻接结点,发现2已经被访问过了,于是访问7
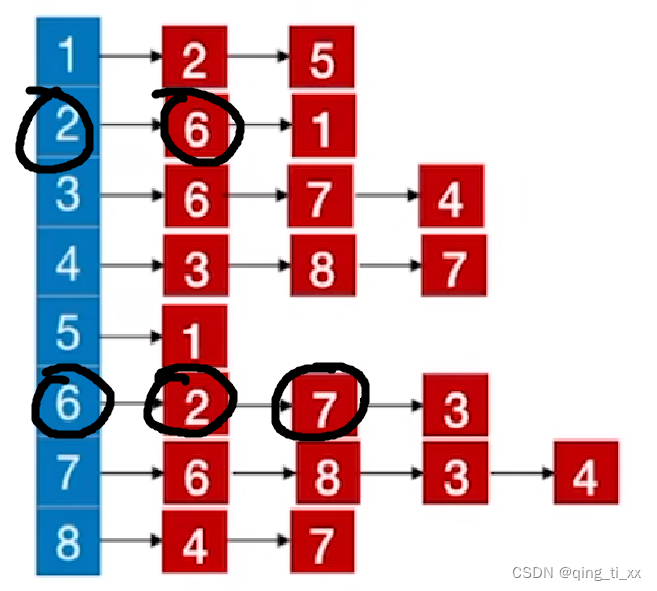
此时,遍历序列为

4、跳转到7,访问7的邻接结点,6被访问过了所以跳过,访问8
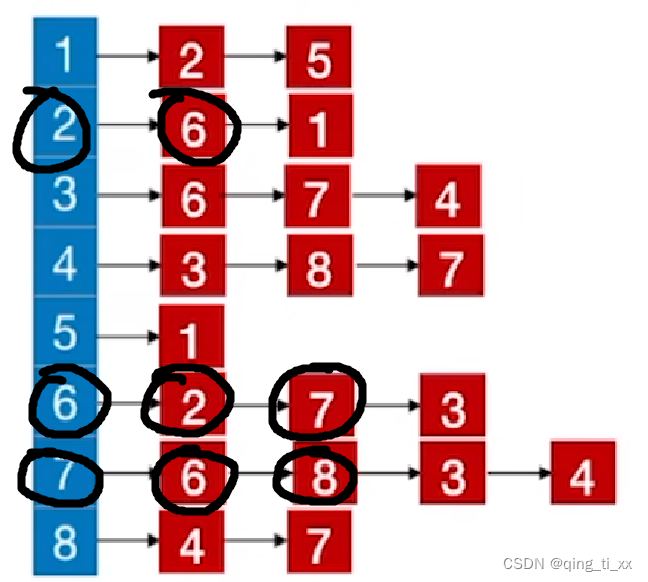
此时,遍历序列为

5、跳转到8,访问8的邻接结点,访问4
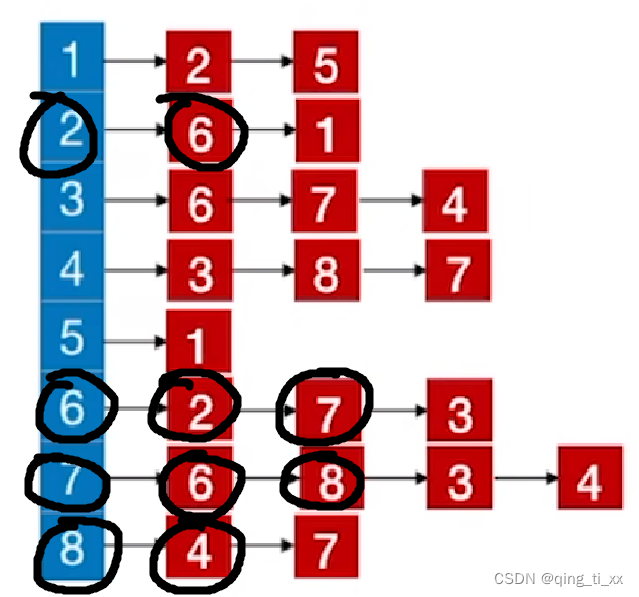
此时,遍历序列为
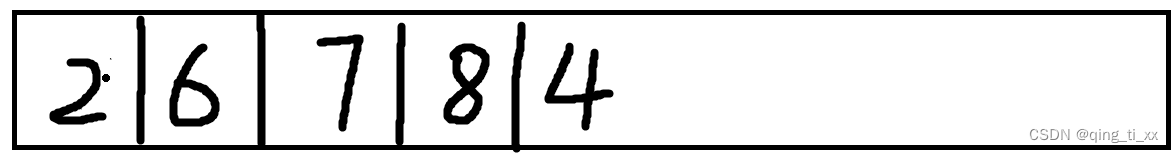
6、继续访问跳转到4,访问4的邻接结点,访问3
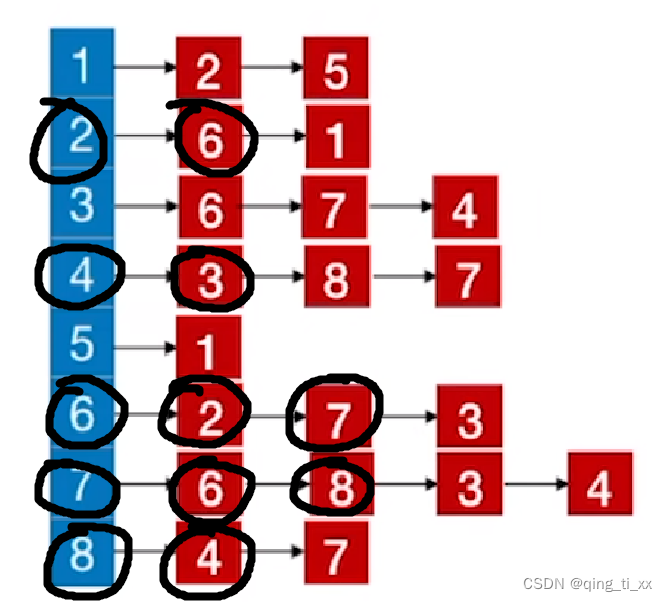
此时,遍历序列为
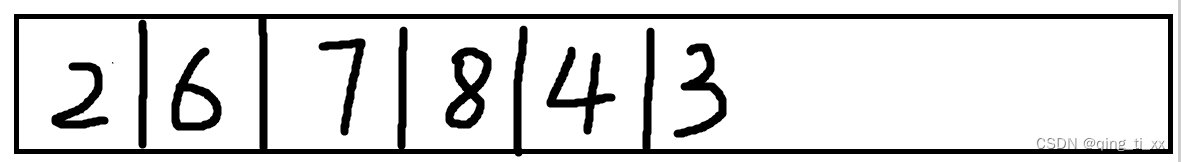
7、跳转到3,访问3的邻接结点,访问6,6被访问过了(跳过),访问7(跳过),访问4(跳过),由于3的邻接结点都被访问完了,所以返回上一级;
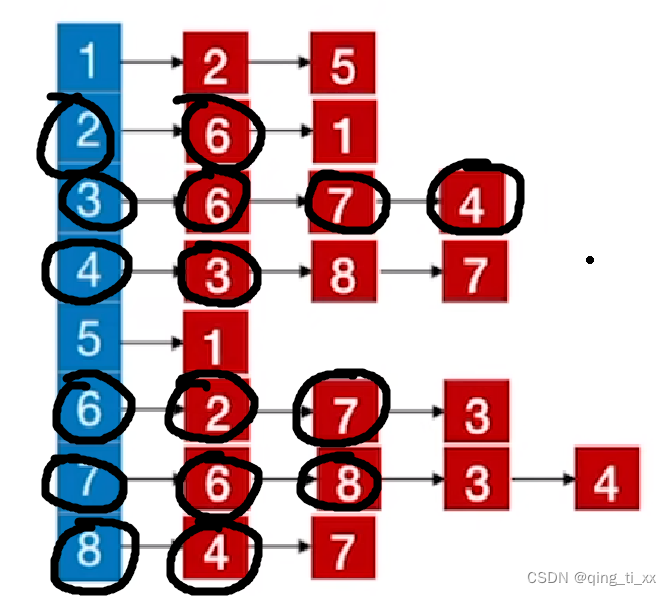
8、遍历4,访问8(跳过),访问7(跳过),返回上一级;
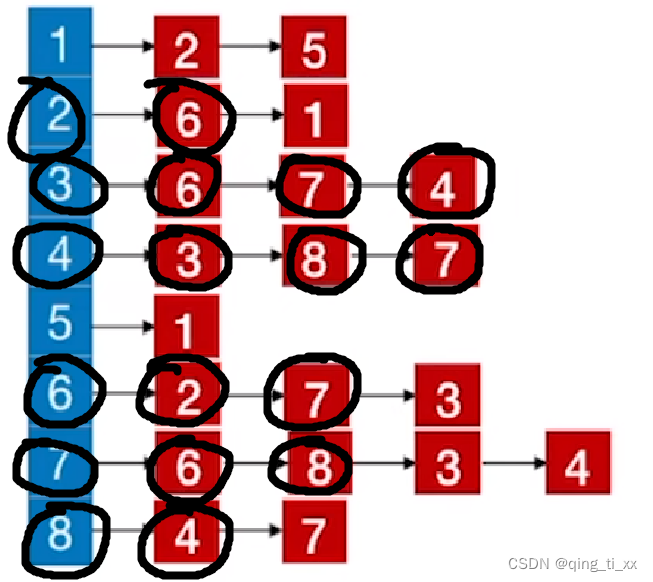
9、上一级是8,所以遍历8,访问7(跳过),返回上一级;
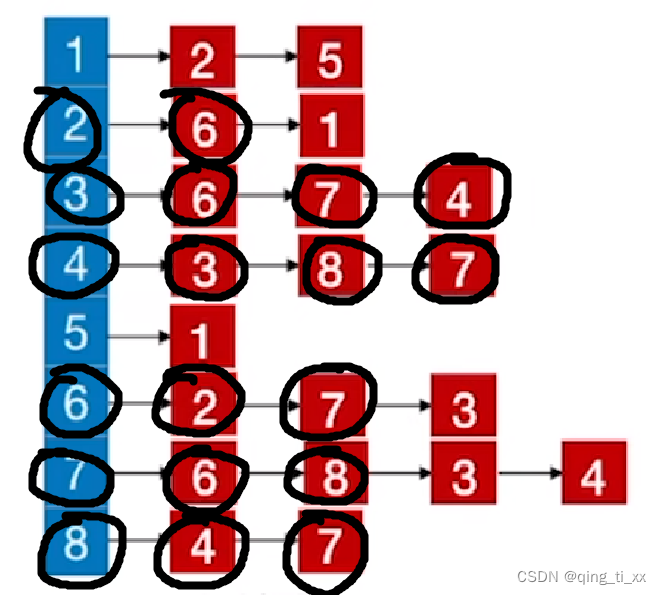
10、遍历7,访问3(跳过),访问4(跳过),返回上一级;
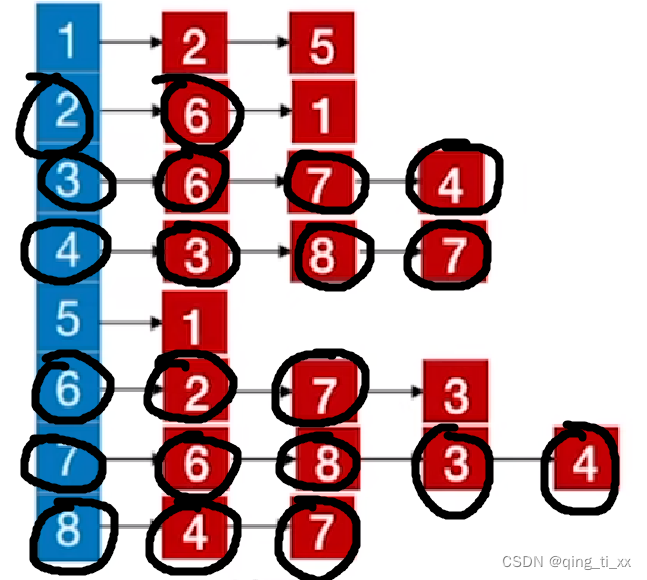
11、遍历6,访问3(跳过),返回上一级;
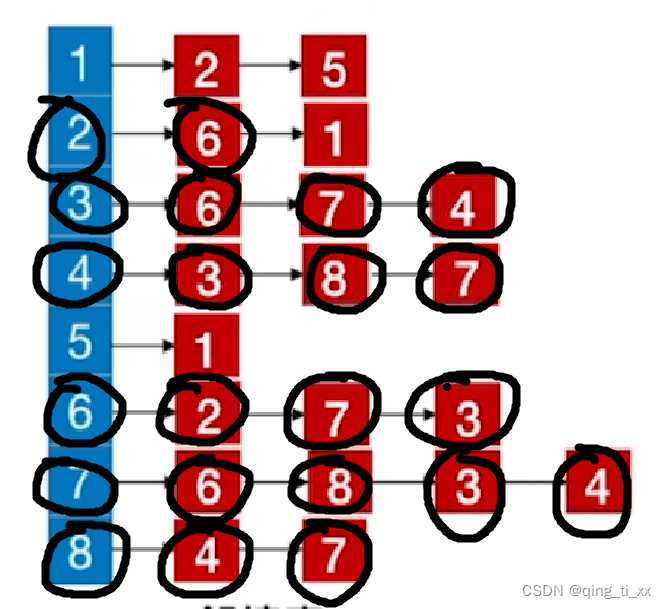
12、遍历2,访问1;
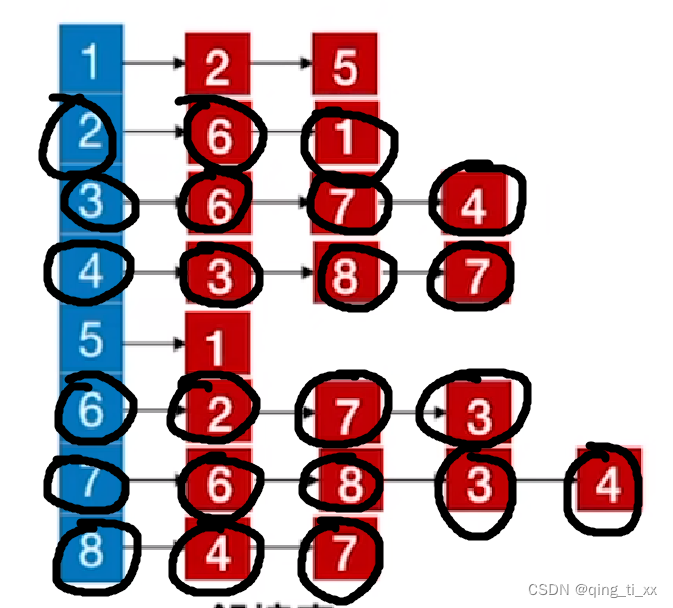
此时,遍历序列为

13、跳转至1,访问2(跳过),访问5;
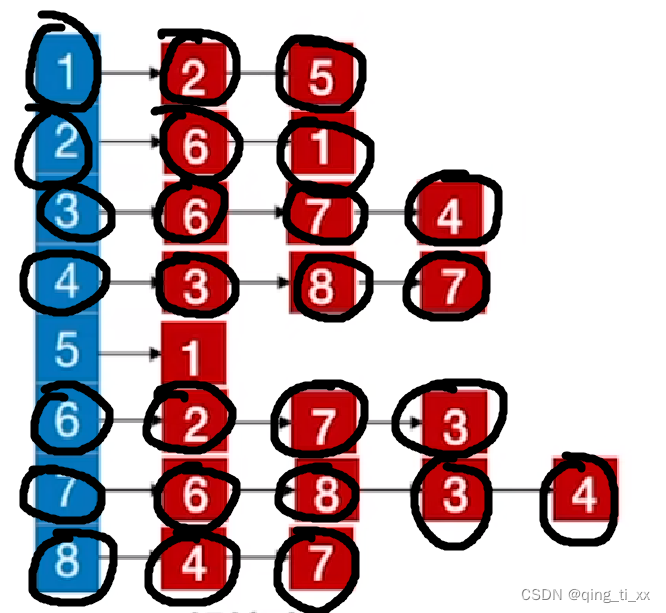
此时,遍历序列为
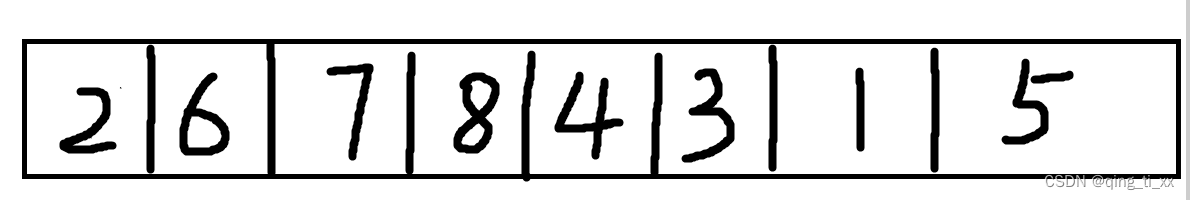
14、跳转至5,访问1,跳过;
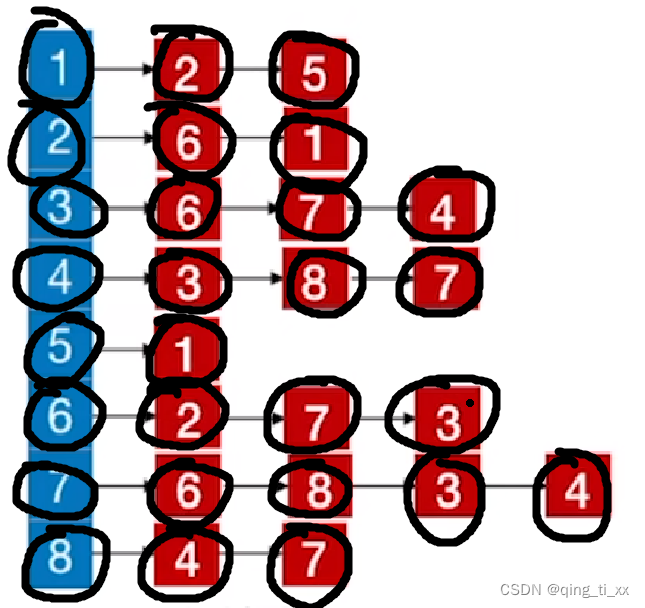
至此,邻接表所有结点全部访问完毕。
得到深度优先遍历序列为:2、6、7、8、4、3、1、5
四、深度优先生成树
与广度优先生成树相似,都是把每个结点第一次被访问的路径提取出来所生成的树,就是生成树
以下图为例:
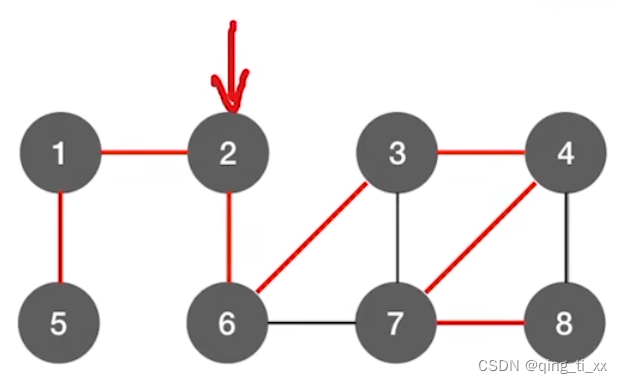
我们从2开始访问,把每个结点第一次被访问的路径标红,这就是生成树。
注意:

五、深度优先生成森林
我们多加一个图
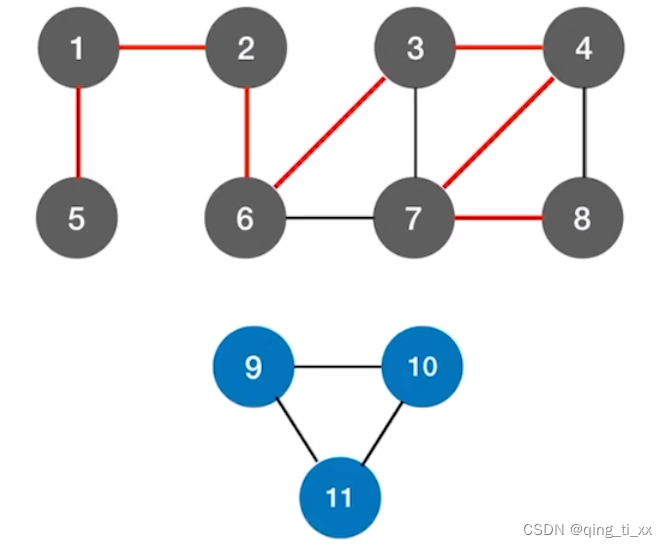
然后表示出它的深度优先生成树,写在一起,就是深度优先生成森林
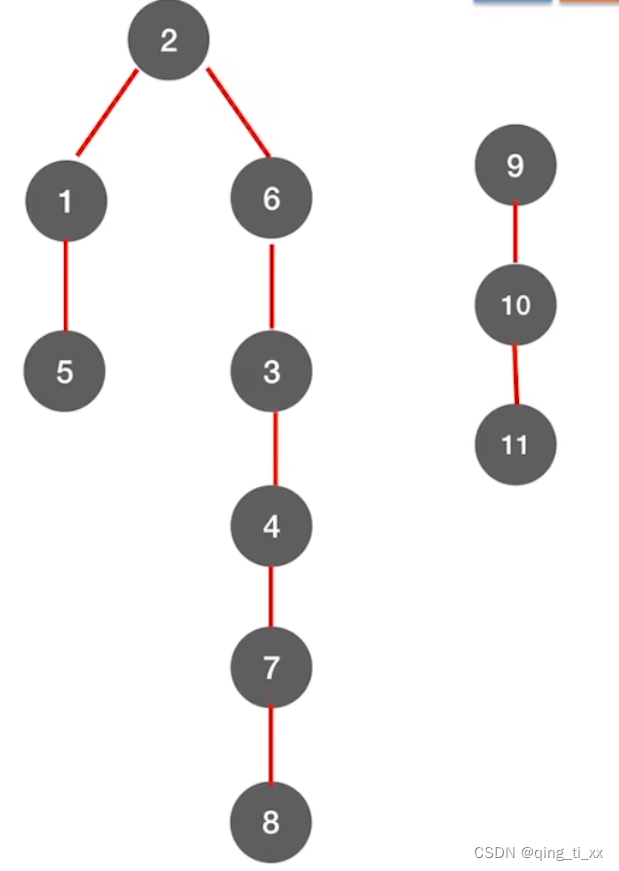
六、图的遍历与图的连通性
无向图:

有向图:
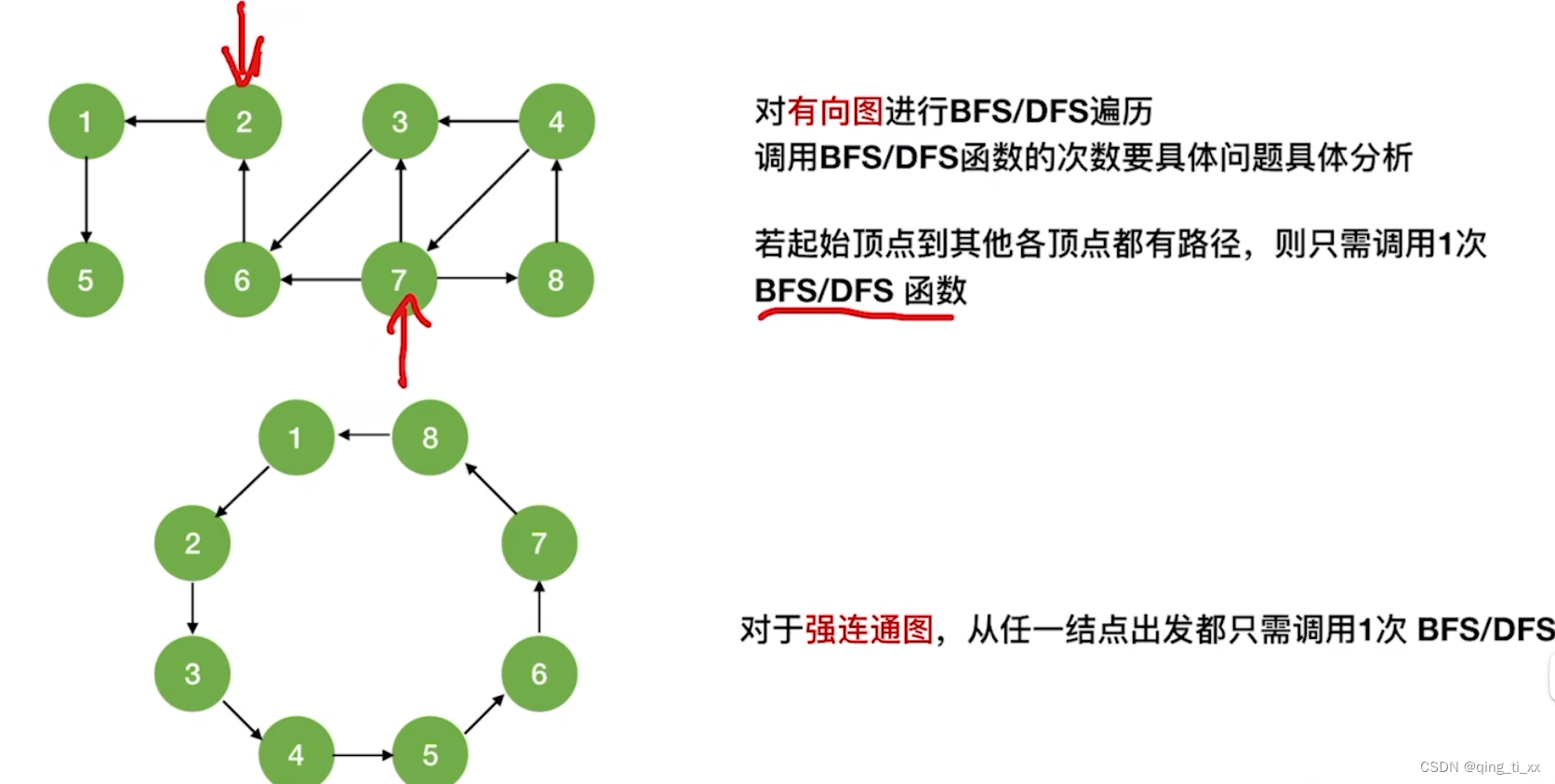
相关文章:

第六章 图 五、图的深度优先遍历(DFS算法)
目录 一、定义 深度优先遍历通常用于解决以下问题: 深度优先遍历算法具有以下优点: 深度优先遍历算法的一个缺点是: 二、代码 空间复杂度: 时间复杂度: 邻接矩阵存储: 邻接表存储: 三、…...

React 中的 useLayoutEffect 钩子函数
useLayoutEffect钩子函数的作用跟useEffect钩子函数的作用一样,它们的不同主要是在于: 1、useEffect钩子函数是异步的,因为此函数在执行的时候是先计算出所有的 Dom 节点的改变后再将对应的 Dom 节点渲染到屏幕上,然而在 useEffe…...
upload-labs1-21关文件上传通关手册
upload-labs文件上传漏洞靶场 目录 upload-labs文件上传漏洞靶场第一关pass-01:第二关Pass-02第三关pass-03:第四关pass-04:第五关pass-05:第六关pass-06:第七关Pass-07第八关Pass-08第九关Pass-09第十关Pass-10第十一…...
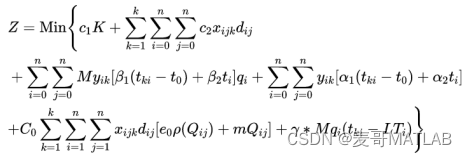
MATLAB遗传算法求解生鲜货损制冷时间窗碳排放多成本车辆路径规划问题
MATLAB遗传算法求解生鲜货损制冷时间窗碳排放多成本车辆路径规划问题实例 1、问题描述 已知配送中心和需求门店的地理位置,并且已经获得各个门店的需求量。关于送货时间的要求,门店都有规定的时间窗,对于超过规定时间窗外的配送时间会产生相应的惩罚成本。为保持生鲜农产品的…...
界面控件DevExpress .NET应用安全 Web API v23.1亮点:支持Swagger模式
DevExpress拥有.NET开发需要的所有平台控件,包含600多个UI控件、报表平台、DevExpress Dashboard eXpressApp 框架、适用于 Visual Studio的CodeRush等一系列辅助工具。 DevExpress 今年第一个重要版本v23.1日前已正式发布了,该版本拥有众多新产品和数十…...
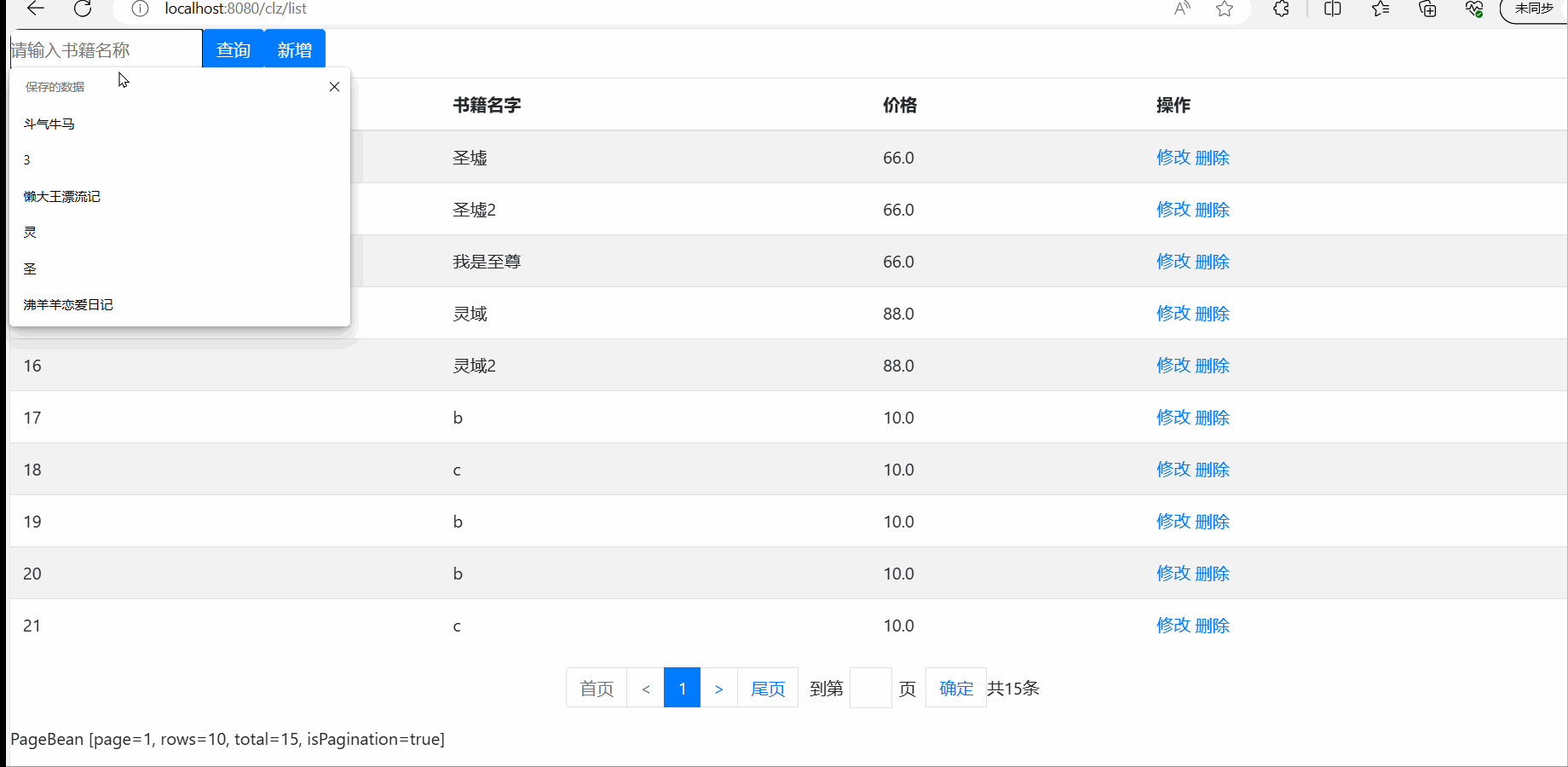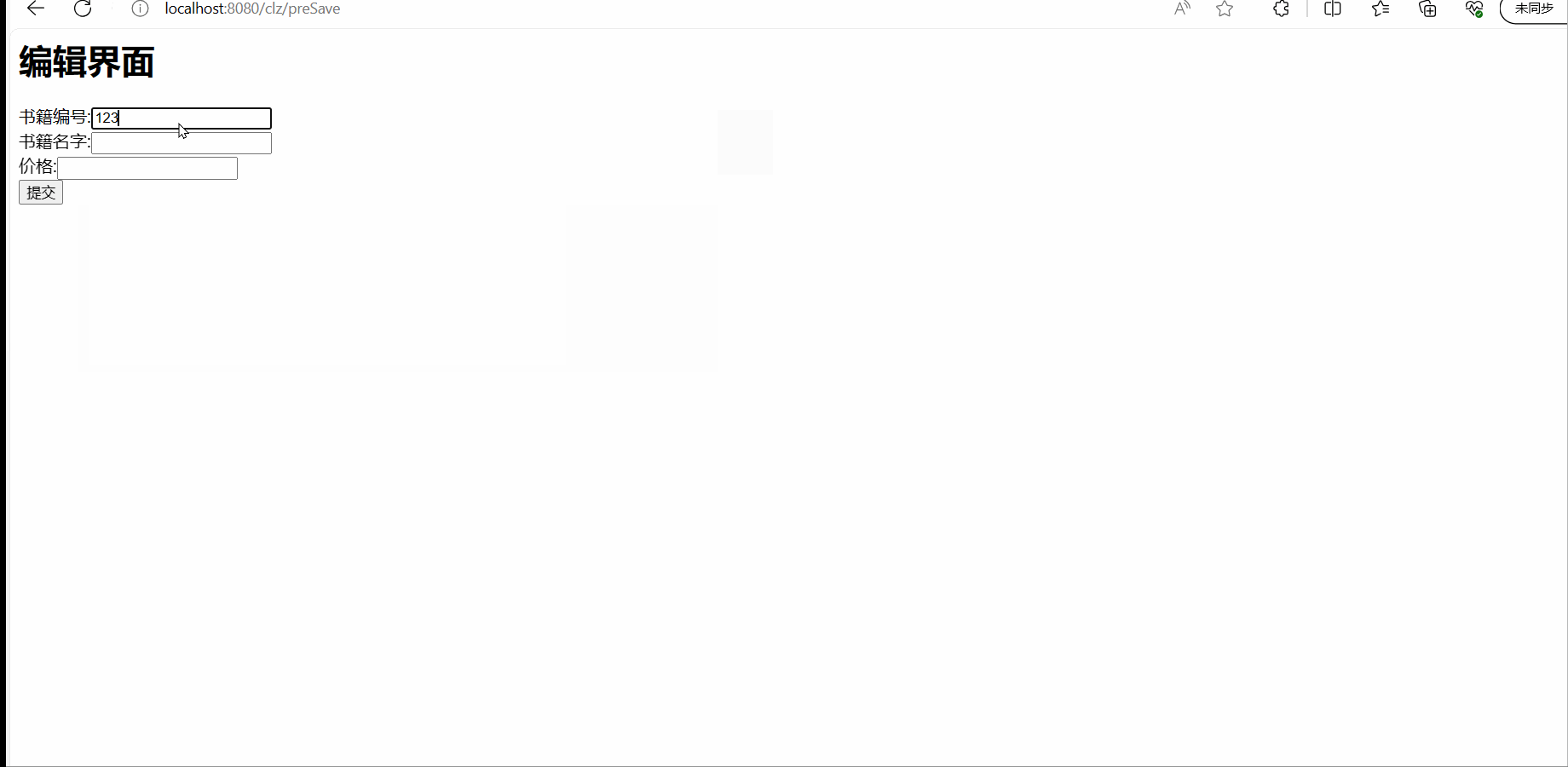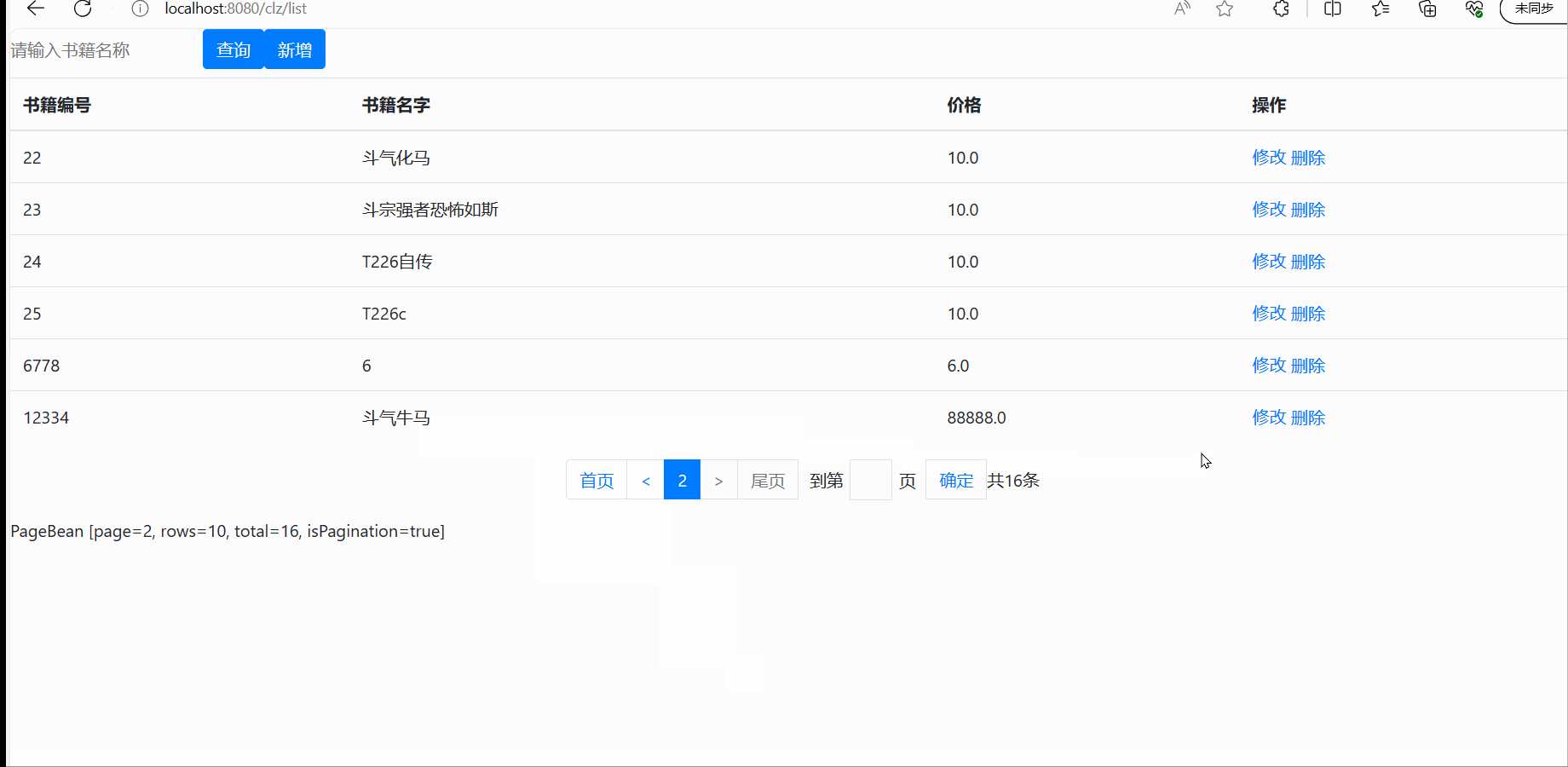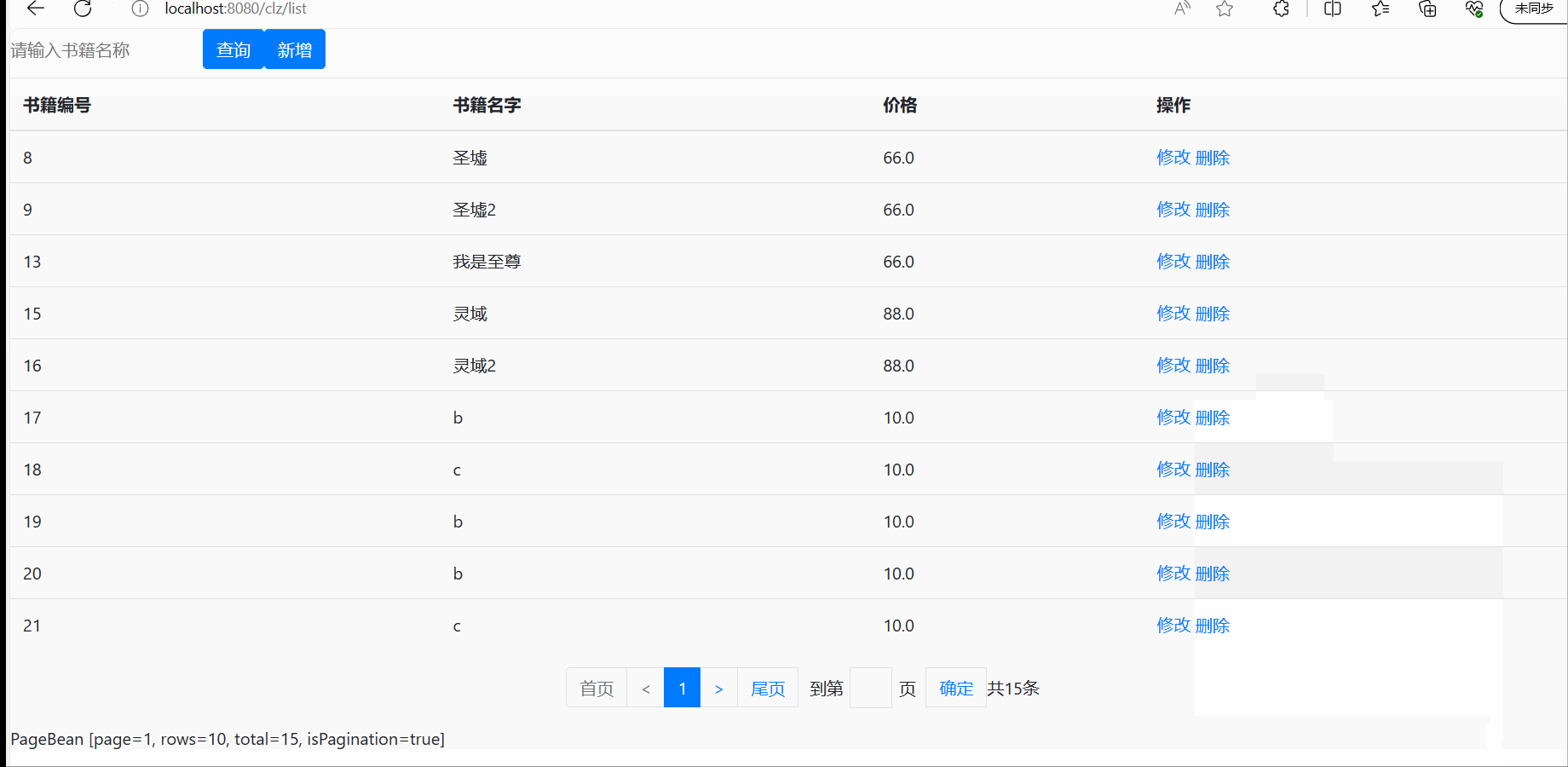
SpringMVC之CRUD------增删改查
目录 前言 配置文件 pom.xml文件 web.xml文件 spring-context.xml spring-mvc.xml spring-MyBatis.xml jdbc.properties数据库配置文件 generatorConfig.xml log4j2日志文件 后台 PageBaen.java PageTag.java 切面类 biz层 定义一个接口 再写一个实现类 …...
- 抖音小程序组件开发)
微信小程序开发教学系列(4)- 抖音小程序组件开发
章节四:抖音小程序组件开发 在本章中,我们将深入探讨抖音小程序的组件开发。组件是抖音小程序中的基本构建块,它们负责展示数据和与用户交互。了解组件的开发方法和使用技巧是进行抖音小程序开发的重要一步。 4.1 抖音小程序的基本组件 抖…...

RabbitMQ反序列化失败:Failed to convert message
🎈 1 参考文档 RabbitMQ消费消息坑:failed to convert serialized Message content | jiuchengi-cnblogs 🔍2 问题描述 org.springframework.amqp.rabbit.support.ListenerExecutionFailedException: Failed to convert messageat org.sprin…...
CTFSHOW 年CTF
1.除夕 php的弱类型,用小数点绕过 这里后面直接加字母不行 2.初三 error_reporting(0); extract($_GET); include "flag.php"; highlight_file(__FILE__); 这里通过extract将get的参数导入为了变量 $_function($__,$___){return $__$___?$___:$__; }; …...
肖sir__设计测试用例方法之状态迁移法05_(黑盒测试)
设计测试用例方法之状态迁移法 一、状态迁移图 定义:通过描绘系统的状态及引起系统状态转换的事件,来表示系统的行为 案例: (1) 订机票案例1: l向航空公司打电话预定机票—>此时机票信息处于“完成”状…...

无涯教程-JavaScript - IMPRODUCT函数
描述 IMPRODUCT函数以x yi或x yj文本格式返回1到255个复数的乘积。两个复数的乘积为- $$(A BI)(C DI)(AC-BD)(A B)1 $$ 语法 IMPRODUCT (inumber1, [inumber2] ...)争论 Argument描述Required/OptionalInumber11 to 255 complex numbers to multiply.Required[inumbe…...
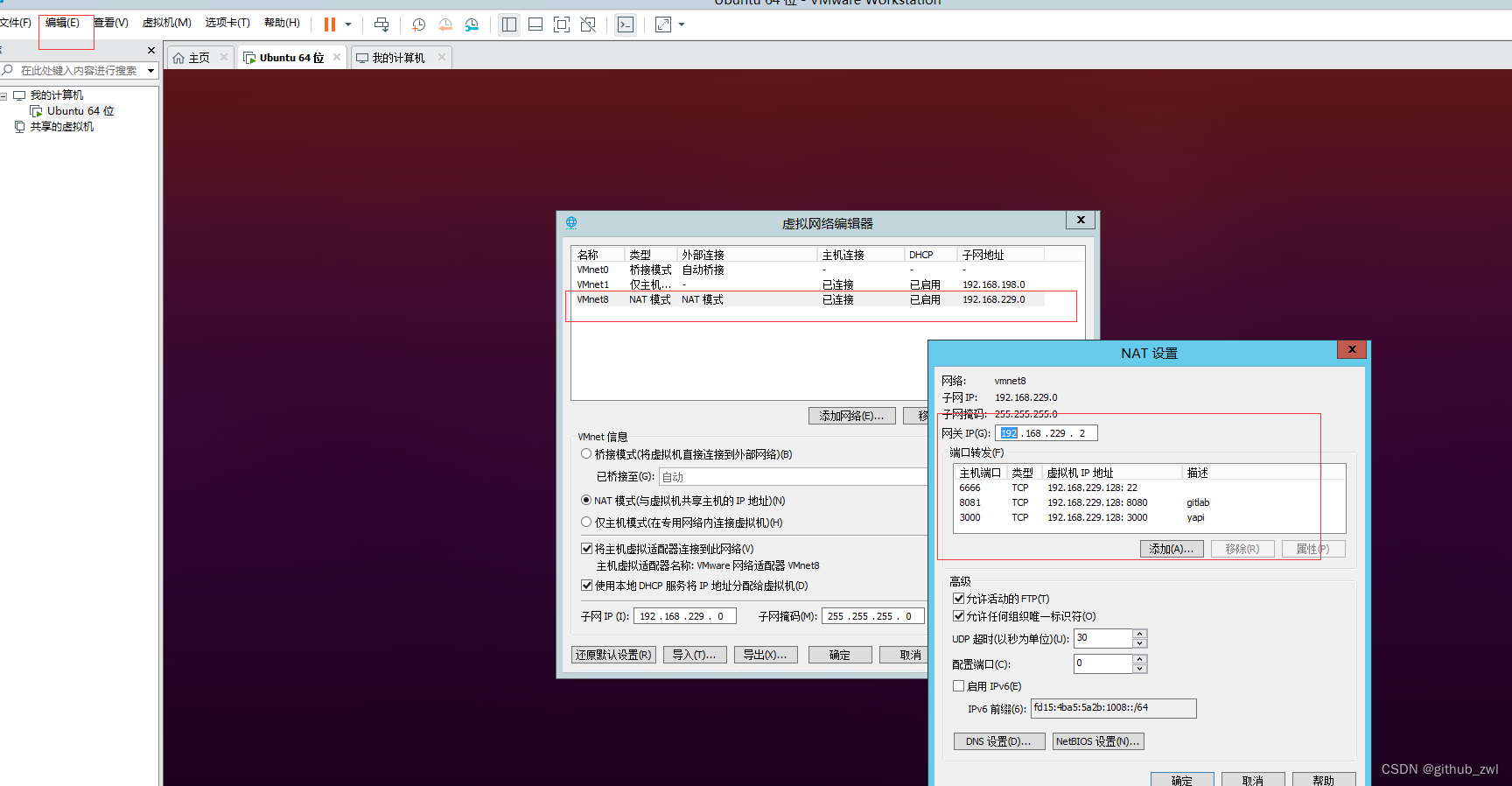
yapi以及gitlab的容器化部署
yapi部署: https://blog.csdn.net/Chimengmeng/article/details/132074922 gitlab部署 使用docker-compose.yml version: 3 services: web: image: twang2218/gitlab-ce-zh:10.5 restart: always hostname: 192.168.xx.xx environm…...

TCP、UDP 协议的区别,各自的应用场景
分析&回答 TCP 传输控制协议,提供的是面向连接、可靠的字节流服务。当客户和服务器彼此交换数据前,必须先在双方之间建立一个TCP连接,之后才能传输数据。TCP提供超时重发,丢弃重复数据,检验数据,流量控制等功能&…...

C高级 DAY3
一、shell中的变量 shell本身是擅长运行指令,是一种弱数据类型语言 它与c语言中定义变量有所不同 C中: 存储类型 数据类型 变量名;shell中: 变量变量的值 ----->如果变量的值中间没有空格直接使用 变量变量的值 ----->变量…...
Linux CentOS7命令及命令行
Linux CentOS7中命令及命令行是非常重要的概念。对大多数初学者来说是既熟悉又了解甚少。本文初步讨论这方面的内容,与同行者交流。 一、命令 命令又称为指令,(英语命令 command,可用简写cmd表示),在终端…...

【C++入门到精通】C++入门 ——搜索二叉树(二叉树进阶)
阅读导航 前言一、搜索二叉树简介1. 概念2. 基本操作⭕搜索操作🍪搜索操作基本代码(非递归) ⭕插入操作🍪插入操作基本代码(非递归) ⭕删除操作🍪删除操作基本代码(非递归࿰…...

学成在线-网站搭建
文章目录 代码素材来自b站pink老师 <!DOCTYPE html> <html lang="en"> <head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>学成在线首…...
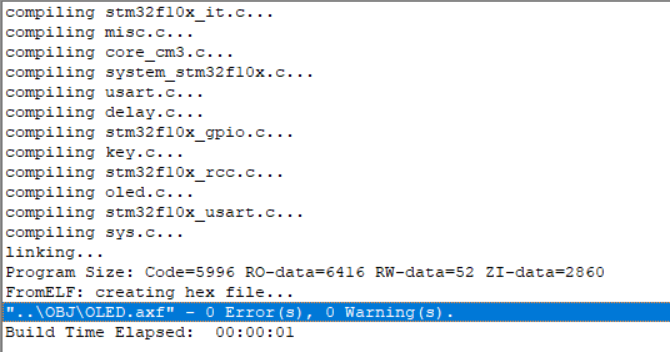
stm32同芯片但不同flash工程更换Device出现报错
目录 1. 问题描述2. 解决方案 1. 问题描述 stm32同芯片但不同flash工程更换Device出现报错 2. 解决方案 更换Device,我是从ZE换为C8: 把这个从HD更换为MD 解决!...

Element UI实现每次只弹出一个Message消息提示
前言 在开发Web应用程序时,我们经常需要使用消息提示来向用户展示重要信息。Element UI提供了一个方便易用的组件——Message,可以用于显示各种类型的消息提示。 然而,默认情况下,当多个消息提示同时触发时,它们会依…...

「网页开发|前端开发|Vue」04 快速掌握开发网站需要的Vue基础知识
本文主要介绍使用Vue进行前端开发的一些必备知识,比如:Vue应用实例,Vue的组件概念,模板语言和模板语法,计算属性,路由配置等等。 文章目录 本系列前文传送门前言一、Vue实例:项目入口二、模板语…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
