【数据结构】AVL树的插入与验证
文章目录
- 一、基本概念
- 1.发展背景
- 2.性质
- 二、实现原理
- ①插入操作
- 1.平衡因子
- 1.1平衡因子的更新
- 1.1.1树的高度变化
- 1.1.2树的高度不变
- 2. 旋转
- 2.1左旋
- 2.2右旋
- 2.3右左双旋
- 2.4 左右双旋
- ②验证
- 1.求二叉树高度
- 2. 判断是否为AVL树
- 源码
- 总结
一、基本概念
1.发展背景
-
普通的二叉搜索树在极端情况下会退化成类似链表的形状,从而使查找的效率降低至O(N)。
-
在此基础上,苏联与以色列数学家
Adelson-Velskii 与 苏联数学家Landis,发明出了 AVL树或者说平衡二叉搜索树。


注:第一张——Adelson-Velskii(1922-2014) ,第二张——Landis(1921——1997)
2.性质
- 左右子树的高度差的绝对值不大于1
- 每个子树都是AVL树。
说明:这样做的目的就是为了严格控制平衡,以便于提高查找效率,但是控制高度差一直为0是不可能的,至于为什么不能控制成0,假设只有两个结点必然存在1的高度差。
二、实现原理
①插入操作
1.平衡因子
英文名:balance factor
- 目的:
保证左右子树的高度差的绝对值不大于1 - 大多数的实现方式:
存放的是右子树与左子树的高度差
1.1平衡因子的更新
1.1.1树的高度变化
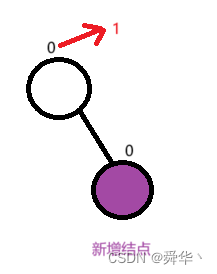
① 左边新增结点
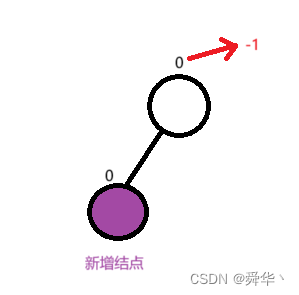
② 右边新增结点
- 总结
- 左边新增,根节点的平衡因子减1
- 右边新增,根节点的平衡因子加1
- 平衡因子从0变为1或者-1
继续分析:
两种情况树的高度增加1,也就是平衡因子从0变为1或者-1,既然高度变化了,可能会导致上面的树不平衡。
如:

此时我们需要向上更新平衡因子,再根据右边高度变化与左边高度变化,决定根的平衡因子加1还是减1。
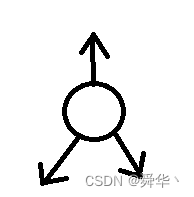
- 推论:
由于可能会向上更新平衡因子,那么AVL树是三叉链的结构。
如图:
1.1.2树的高度不变
① 左边新增结点
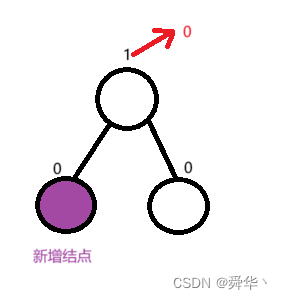
② 右边新增结点
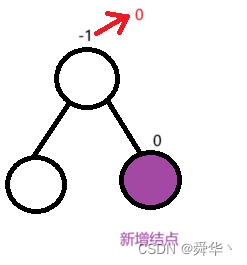
- 同理
- 左边新增,根节点的平衡因子减1
- 右边新增,根节点的平衡因子加1
- 平衡因子由1或者-1变为0
继续分析,这里的根节点的所在树的高度即——左右子树高度的最大值 + 1(根节点的高度)
左右子树的高度的最大值不变,即这颗树高度不变,即不用往上继续更新且达到平衡。
2. 旋转
-
说明:旋转就是让
不平衡的树再次平衡的手段。 -
条件:平衡因子为2或者-2,即高度差的绝对值为2。
-
补充:若平衡因子大于等于3,说明当前树就不是AVL树,需要检验之前的代码。
但是我们又得对情况进行分类讨论,因为不同情况让树再次平衡的旋转方式不同。
2.1左旋
- 说明:也就是右边高度高,需要旋转来降低右边的高度,进而达到平衡。
一步一步分析,先来个最简单的:

此时,旋转过后平衡因子全变为0,且当前树达到平衡。注意此时3结点的左结点为空!(细节)
再举一个例子:
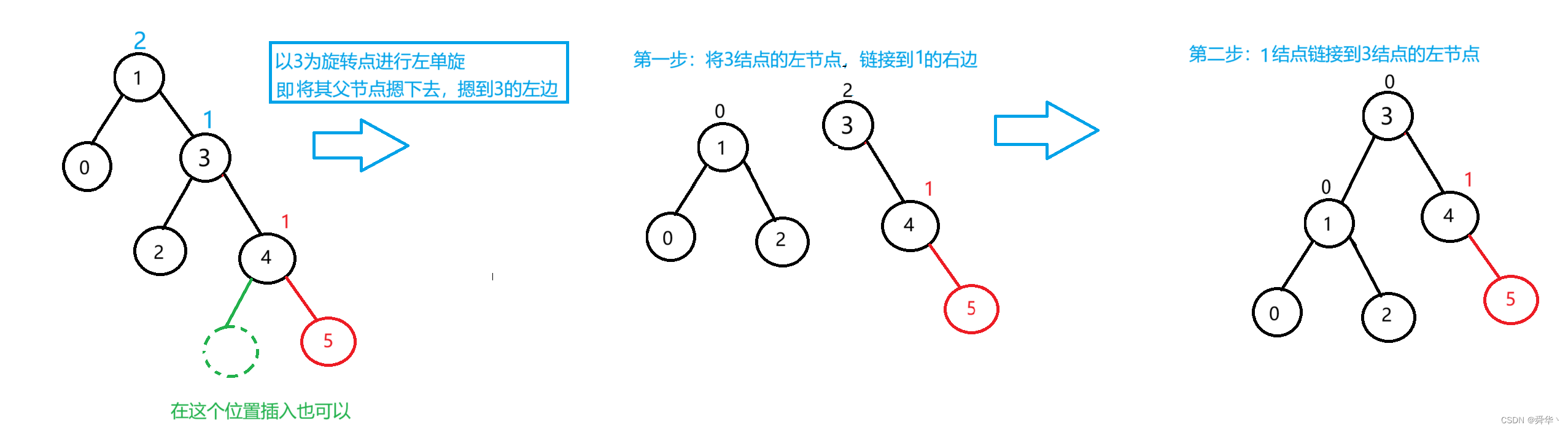
此时,旋转过后平衡因子1和3的平衡因子变为0,且当前树达到平衡,此时我们是不用管其它子树的,因为子树必然是AVL树,要不然更不到根节点就停止了。
最后来一个稍微复杂的例子:
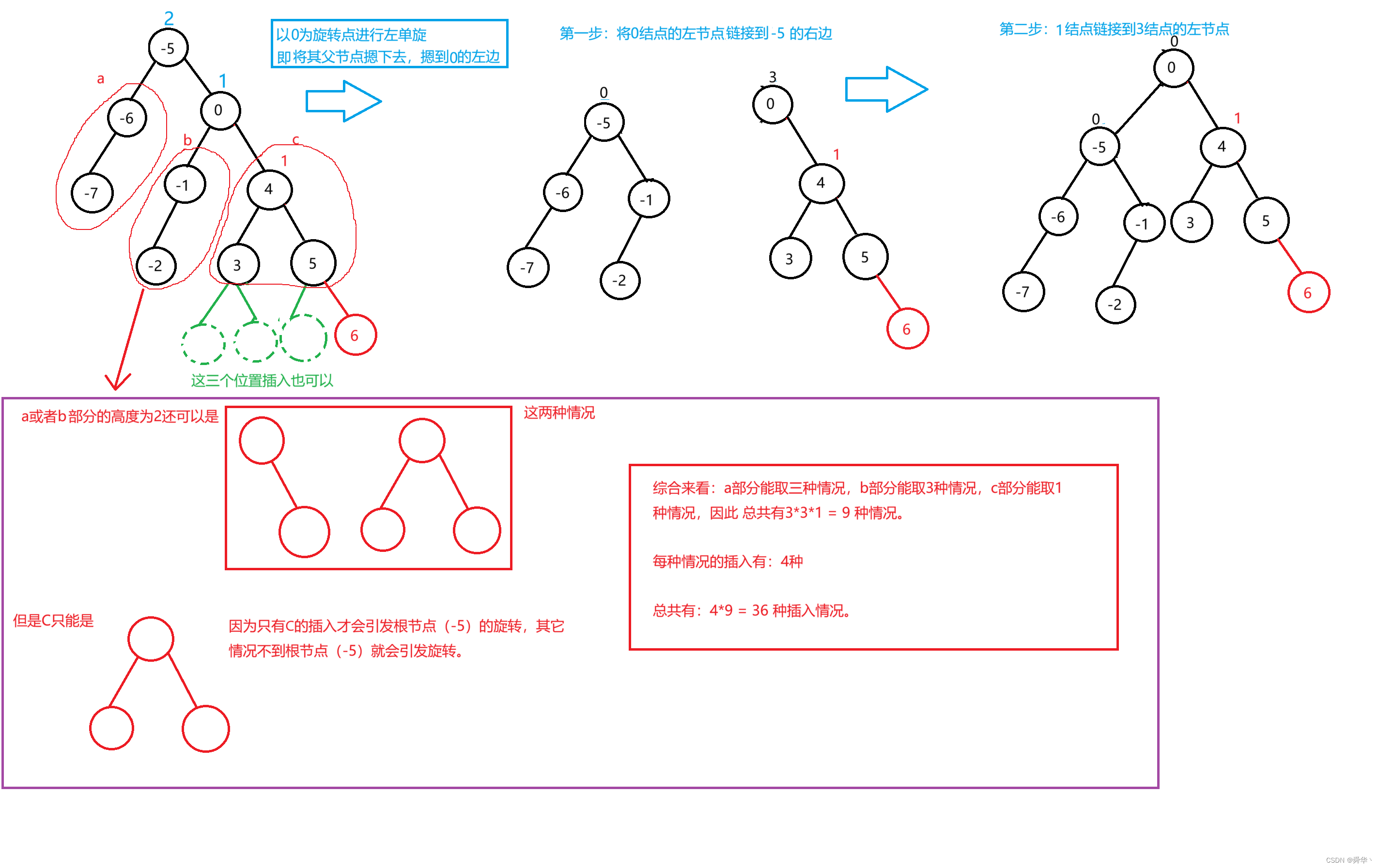
此时,旋转过后平衡因子-5和0的平衡因子变为0,且当前树达到平衡。
这是具体的图便于辅助理解,然后我们再画出所有情况的抽象图:
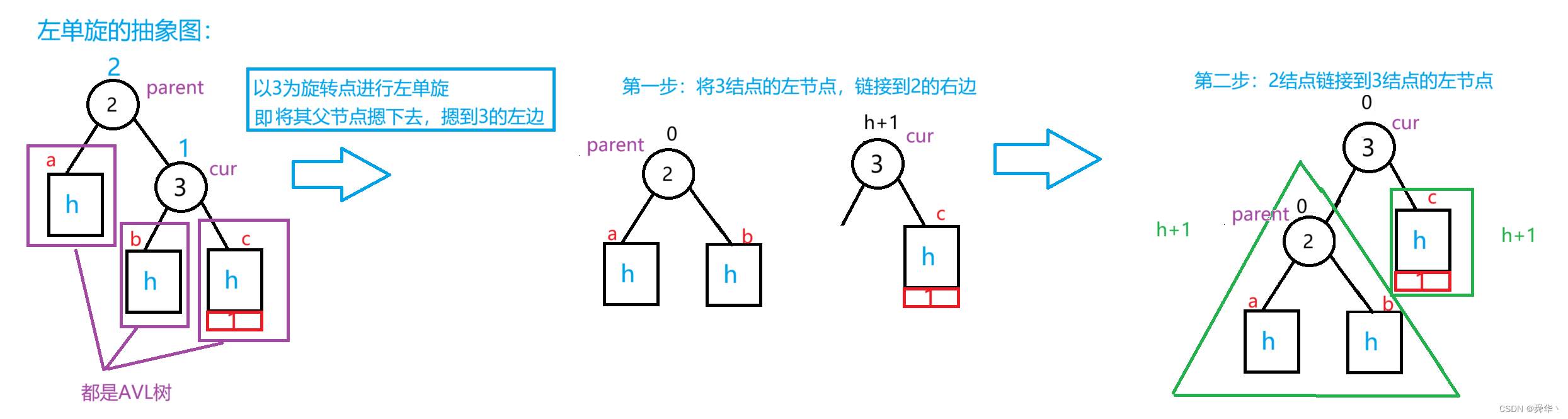
- 总结
只能在c部分上插入结点才可能会引发根节点左单旋,也就是说parent的右边为cur且新增结点在cur的右边。- 旋转过后
cur与parent的平衡因子变为0。
- 细节
- b的父节点连接parent时,需要判断b部分是否为空。
- parent的父节点连接cur时,需要保存一下parent的父节点。
- 根据parent的父节点判断是否需要修改根节点,若为空则修改,若不为空,则将cur链接到parent的父节点,同时更新parent父节点的指向。
- 实现代码
void RotateL(Node* parent){//画图分析://操作的结点有cur,cur_left,ppnodeNode* cur = parent->_right;Node* cur_left = cur->_left;//将parent的右节点改为cur_leftparent->_right = cur_left;//改变cur_left父节点的转向//cur_left可能为空if (cur_left != nullptr){cur_left->_parent = parent;}//将parent链接在cur的左边//为了更新cur的parent需要保存parent的父节点Node* ppnode = parent->_parent;cur->_left = parent;parent->_parent = cur;//ppnode可能为空if (ppnode == nullptr){//需要修改根节点_root = cur;cur->_parent = nullptr;}else{//改变ppnode的指向if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}
2.2右旋
说明:也就是左边高度高,需要旋转来降低右边的高度,进而达到平衡。
跟左旋的分析方式一样。
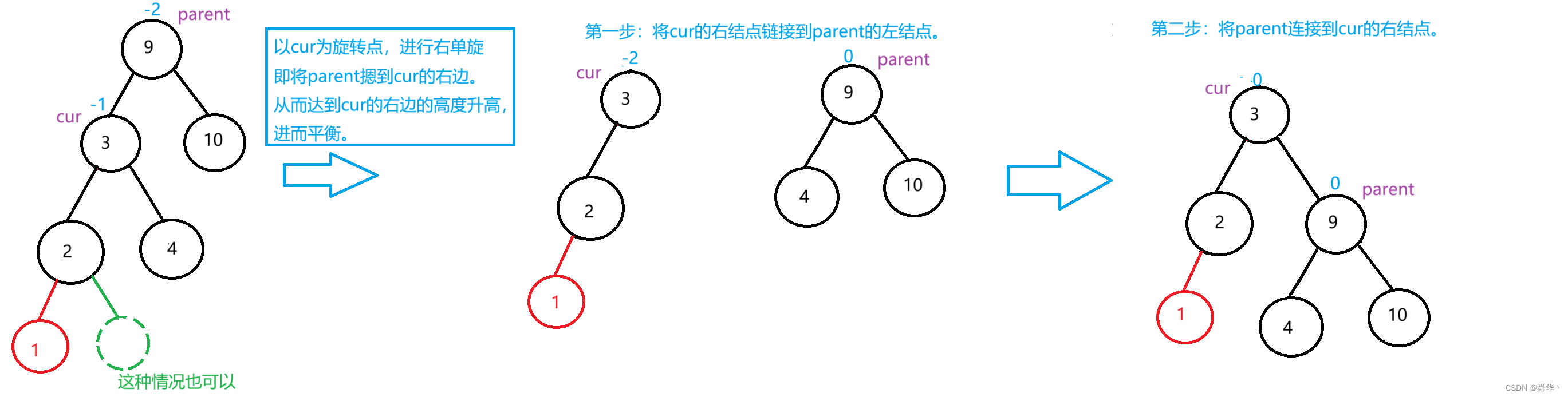
先来个简单的感受一下:

此时,旋转过后平衡因子parent和cur的平衡因子变为0,且当前树达到平衡。
再举一个例子:
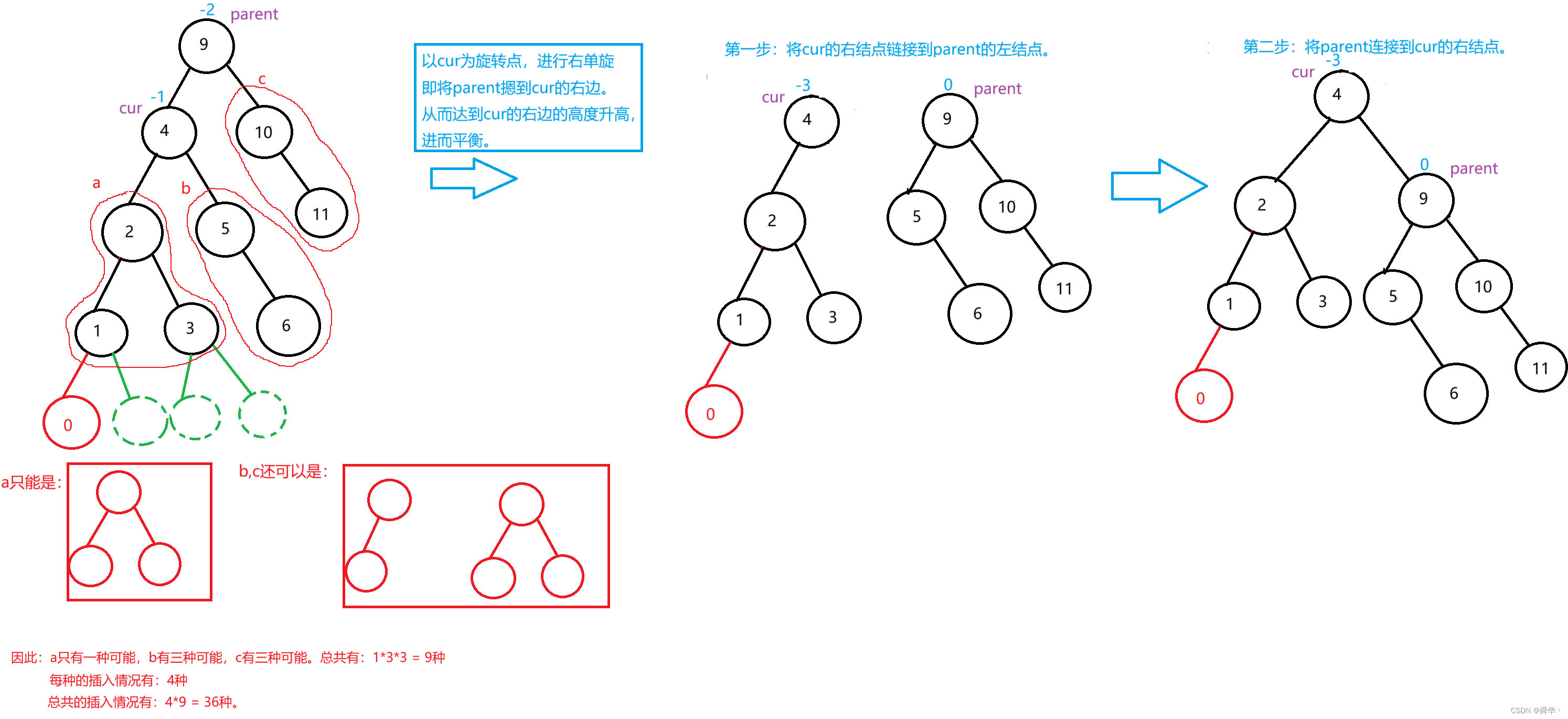
最后来一个稍微复杂的例子:
画出所有情况的抽象图:
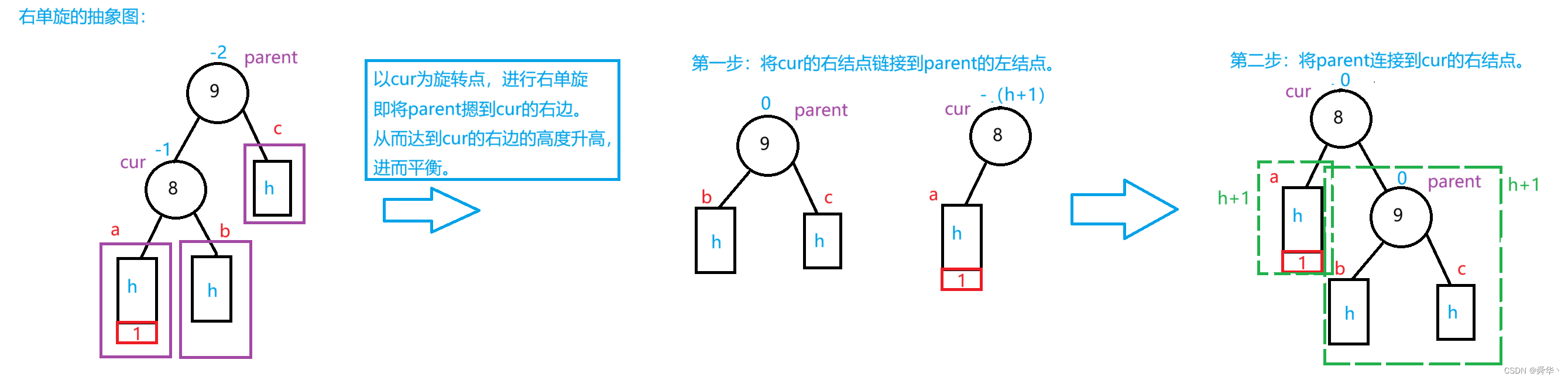
- 总结
只能在a部分上插入结点才可能会引发根节点右单旋,也就是说parent与cur与高度变化的c树的根节点在同一个方向且在parent的左- 旋转过后
cur与parent的平衡因子变为0。
- 细节——同左旋
- b的父节点连接parent时,需要判断b部分是否为空。
- parent的父节点连接cur时,需要保存一下parent的父节点。
- 根据parent的父节点判断是否需要修改根节点,若为空则修改,若不为空,则将cur链接到parent的父节点,同时更新parent父节点的指向。
- 实现代码:
void RotateR(Node* parent){//操作的结点Node* cur = parent->_left;Node* cur_right = cur->_right;//第一步:将cur_right链接到parent的leftparent->_left = cur_right;//更改cur_right的父节点//注意:cur_right可能为空if (cur_right != nullptr){cur_right->_parent = parent;}//第二步:将parent链接到cur的右结点。//先保存一下parent的父节点Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;//ppnode为空说明需要修改根节点if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}
2.3右左双旋
- 可以简单理解为,需要进行处理的左旋。
说明:单旋无法解决问题,原因是发生了拐弯,需要用右旋讲折线变为直线,再进行左旋。
因为情况有点多我们就来个简单的,直接化抽象图,看结论比较容易理解。
先来个简单的:
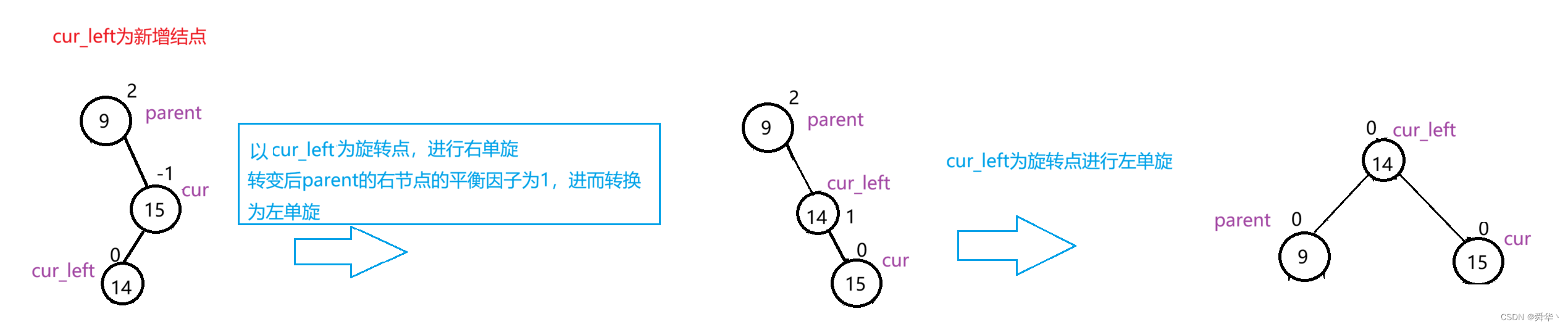
先右旋之后折线变成了直线,变成了左旋的形状,再进行左旋,最后的cur与cur_left与parent的平衡因子变成了0,最终cur_left变成了根节点。
再化抽象图:
初始状态
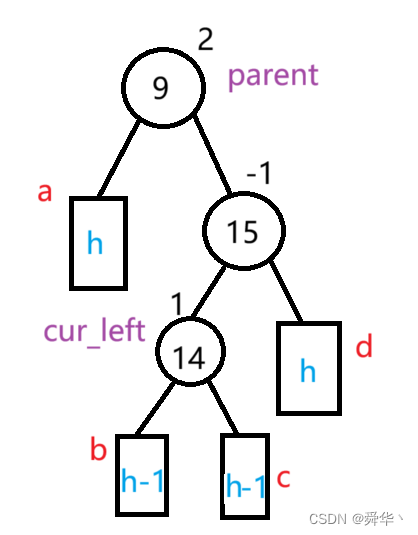
还是一样,不过得分两种情况进行讨论:
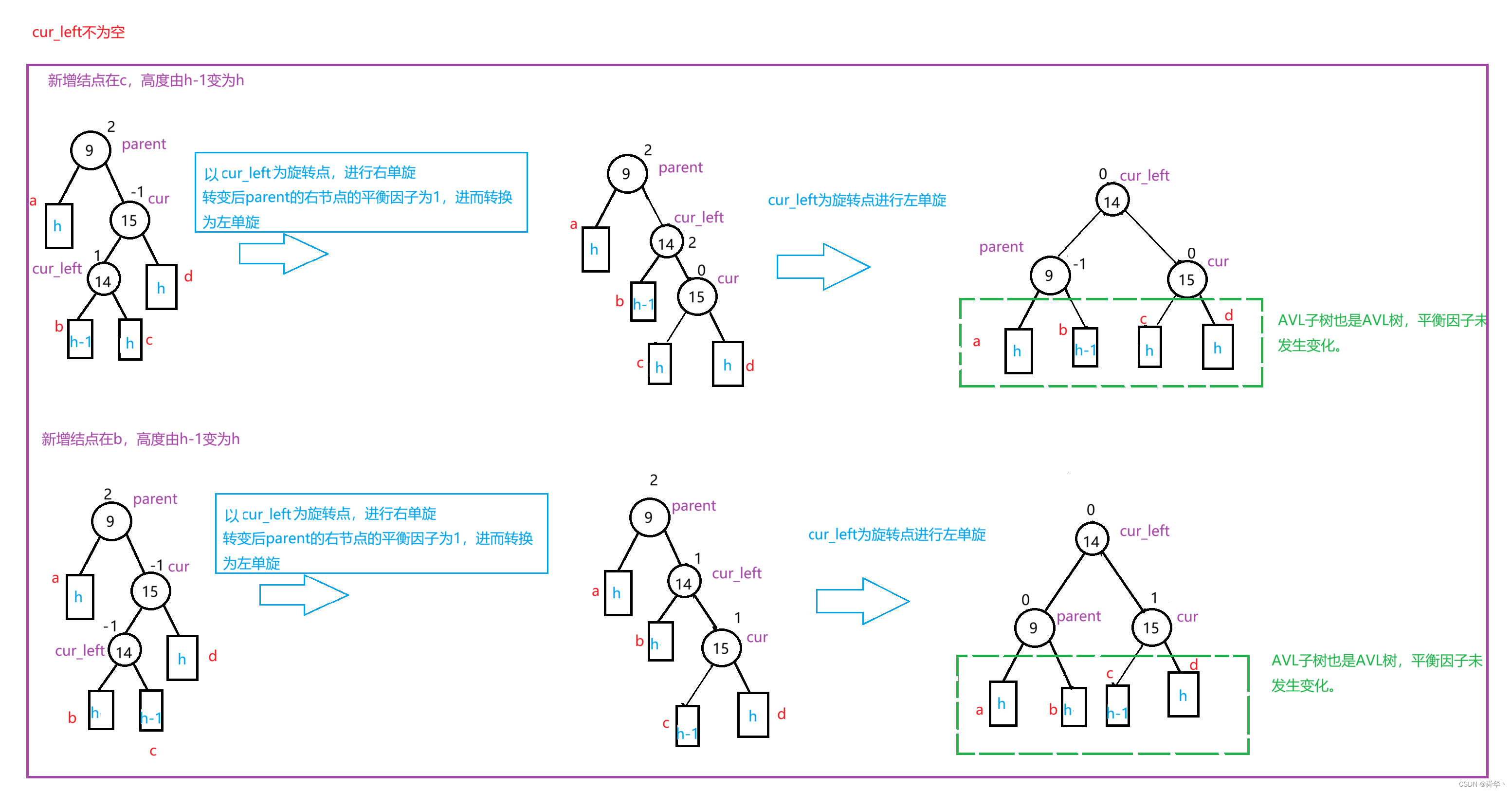
- 新增结点在c树上,会导致parent的平衡因子变为-1,cur的平衡因子变为0。
- 新增结点在b树上,会导致parent的平衡因子变为0,cur的平衡因子变为1
- 不管新增结点在谁上,cur_left的平衡因子都为0。
-
看图分析,其实不看新增结点在谁身上,两种最终的旋转的结果是一样的,那我们其实只需先不看新增结点再画图,根据最终的结果再把新增结点添上,其实会更加直观。
-
总结
- 新增结点在c树上,会导致parent的平衡因子变为-1,cur的平衡因子变为0。
- 新增结点在b树上,会导致parent的平衡因子变为0,cur的平衡因子变为1。
- cur_left为新增结点,parent与cur的结点全为0。
- 实现代码:
void RotateRL(Node* parent){Node* cur = parent->_right;Node* cur_left = cur->_left;//CL——CurLeftint CL_bf = cur_left->_bf;RotateR(cur);RotateL(parent);//更新平衡因子if (CL_bf == 0){cur->_bf = parent->_bf = cur_left->_bf = 0;//虽然没必要,但是起到了解耦的作用。}else if (CL_bf == 1){parent->_bf = -1;cur->_bf = cur_left->_bf = 0;}else if(CL_bf == -1){cur->_bf = 1;parent->_bf = cur_left->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}
2.4 左右双旋
- 可以理解为,需要进行处理的右旋。
说明:单旋无法解决问题,原因是发生了拐弯,需要用左旋讲折线变为直线,再进行右旋。
分析方法跟右左双旋一样。
先来个简单的:
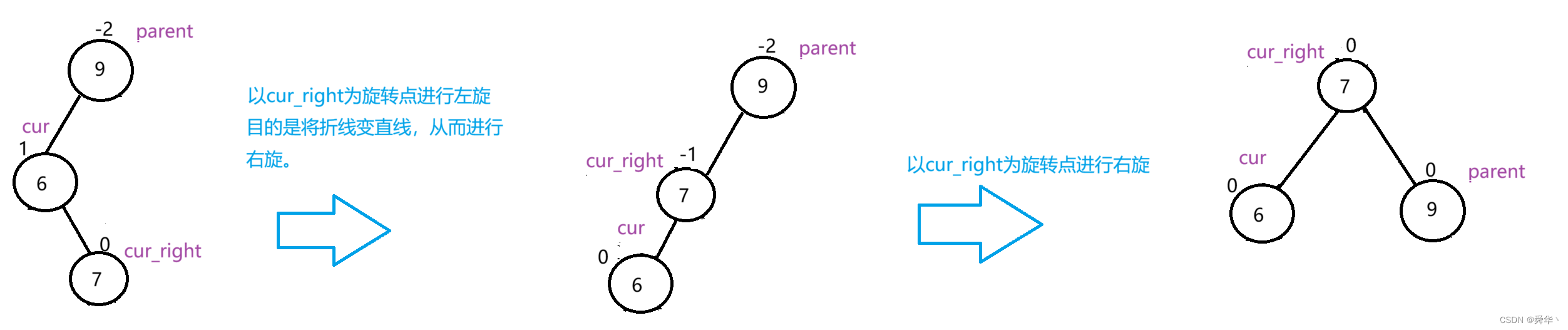
先左旋之后折线变成了直线,变成了右旋的形状,再进行右旋,最后的cur与cur_left与parent的平衡因子变成了0,最终cur_left变成了根节点。
再来个抽象的:
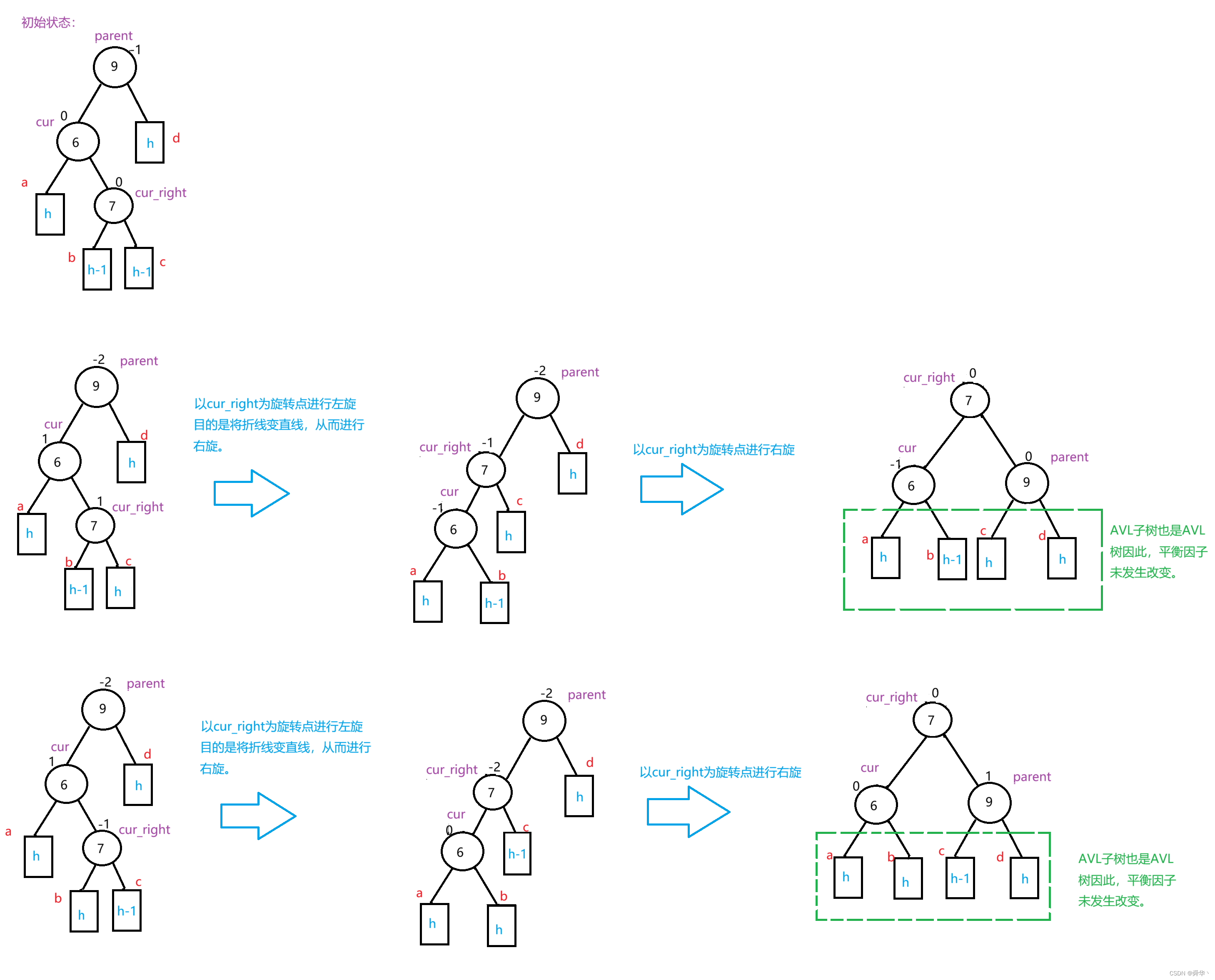
还是一样,不过得分两种情况进行讨论:
- 新增结点在c树上,会导致cur的平衡因子变为-1,parent的平衡因子变为0。
- 新增结点在b树上,会导致cur的平衡因子变为0,parent的平衡因子变为1
- 不管新增结点在谁上,cur_right的平衡因子都为0。
- 总结
- cur_right平衡因子为1,说明新增结点在b树上,会导致cur的平衡因子变为0,parent的平衡因子变为1。
- cur_right的平衡因子为-1,新增结点在c树上,会导致cur的平衡因子变为-1,parent的平衡因子变为0。
- cur_right的平衡因子为0,cur与parent的平衡因子都变为0。
- 不管新增结点在谁上,cur_right的平衡因子都为0。
- 代码实现
void RotateLR(Node* parent){Node* cur = parent->_left;Node* cur_right = cur->_right;int CR_bf = cur_right->_bf;RotateL(cur);RotateR(parent);if (CR_bf == 0){parent->_bf = cur->_bf = cur_right->_bf = 0;}else if(CR_bf == 1){cur->_bf = -1;parent->_bf = cur_right->_bf = 0;}else if (CR_bf == -1){parent->_bf = 1;cur->_bf = cur_right->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}
②验证
说明:
- 根据定义验证每颗子树的高度差
- 需要判断当前的右子树的高度差是否等于平衡因子
直接根据平衡因子进行判断,有点监守自盗的感觉,你能保证自己更新的平衡因子就是正确的么?我都不敢保证。
1.求二叉树高度
- 后序遍历
size_t Height(Node* root){if (root == nullptr){return 0;}int LHeight = Height(root->_left);int RHeight = Height(root->_right);return max(LHeight, RHeight) + 1;}
2. 判断是否为AVL树
bool _IsAVLTree(Node* root){if (root == nullptr){return true;}int RHeight = Height(root->_right);int LHeight = Height(root->_left);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){return false;}return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);}
优化一下:
bool IsAVLTree(){bool is_AVL = true;_IsAVLTree(_root, is_AVL);return is_AVL;}int _IsAVLTree(Node* root,bool& is_AVL){if (root == nullptr){return 0;}int RHeight = _IsAVLTree(root->_right, is_AVL);int LHeight = _IsAVLTree(root->_left, is_AVL);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){is_AVL = false;}return max(RHeight, LHeight) + 1;}
源码
#include<iostream>
#include<assert.h>
using namespace std;
namespace MY_STL
{template<class Key,class Val>struct AVLTreeNode{typedef AVLTreeNode<Key, Val> Node;AVLTreeNode(const pair<Key,Val>& key = pair<Key,Val>()):_key(key.first),_val(key.second),_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0){}Key _key;Val _val;//三叉链的结构Node* _left;Node* _right;Node* _parent;int _bf;};template<class Key, class Val>class AVLTree{typedef AVLTreeNode<Key, Val> Node;public:AVLTree(){}bool insert(const pair<Key,Val>& val){//第一步:插入操作//如果根节点为空if (_root == nullptr){_root = new Node(val);return true;}else{Node* cur = _root,*parent = _root;while (cur){if (cur->_key > val.first){parent = cur;cur = cur->_left;}else if(cur->_key < val.first){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(val);if (parent->_key > val.first){parent->_left = cur;}else{parent->_right = cur;}//更新新增结点的_parentcur->_parent = parent;//第二步:更新平衡因子//平衡因子://1. 定义为右子树的高度减去左子树的高度//2. 合法范围为{-1,0,1}//3. 新增结点在左,父节点的平衡因子减1//4. 新增结点在右,父节点的平衡因子加1//5. 当父节点的平衡因子变为0——由-1变0或者1变0时,此时AVL树的高度不变//6. 当父节点的平衡因子变为1或者-1,AVL子树的高度变化,继续向上变化。//7. 当父节点的平衡因子变为2或者-2时,此时需要旋转,进行平衡//8. 当父节点为根节点时,此时需要结束循环。while (cur != _root){//更新平衡因子if (parent->_left == cur){//左减1(parent->_bf)--;}else{//右加1(parent->_bf)++;}//判断平衡因子if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = cur->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){//对旋转进行分类讨论//if (parent->_bf == 2 && cur->_bf == 1)//{// //左单旋// RotateL(parent);//}//else if (parent->_bf == -2 && cur->_bf = -1)//{// //右单旋// RotateR(parent);//}//else if (parent->_bf == 2 && cur->_bf == -1)//{// RotateRL(parent);//}//else if (parent->_bf == -2 && cur->_bf == 1)//{// RotateLR(parent);//}if (parent->_bf == 2){//左单旋if (cur->_bf == 1){RotateL(parent);}else{RotateRL(parent);}}else{//右单旋if (cur->_bf == -1){RotateR(parent);}else{RotateLR(parent);}}//旋转完成,树达到平衡break;}}return true;}}//根据定义进行判断bool IsAVLTree(){bool is_AVL = true;_IsAVLTree(_root, is_AVL);return is_AVL;//return _IsAVLTree(_root);}void Print(){_InOrder(_root);cout << endl;}//根据平衡因子进行判断//bool IsAVLTree()//{// return _IsAVLTree(_root);//}private:void _InOrder(Node* root){if (root == nullptr){return;}_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}//bool _IsAVLTree(Node* root)//{// if (root == nullptr)// return true;// if (root->_bf >= 2 || root->_bf <= -2)// {// return false;// }// else// {// return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);// }//}//bool IsAVLTree()//{// bool is_AVL = true;// _IsAVLTree(_root, is_AVL);// return is_AVL;//}size_t Height(Node* root){if (root == nullptr){return 0;}int LHeight = Height(root->_left);int RHeight = Height(root->_right);return max(LHeight, RHeight) + 1;}int _IsAVLTree(Node* root,bool& is_AVL){if (root == nullptr){return 0;}int RHeight = _IsAVLTree(root->_right, is_AVL);int LHeight = _IsAVLTree(root->_left, is_AVL);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){is_AVL = false;}return max(RHeight, LHeight) + 1;}bool _IsAVLTree(Node* root){if (root == nullptr){return true;}int RHeight = Height(root->_right);int LHeight = Height(root->_left);if (abs(RHeight - LHeight) > 1 || root->_bf != RHeight - LHeight){return false;}return _IsAVLTree(root->_left) && _IsAVLTree(root->_right);}void RotateLR(Node* parent){Node* cur = parent->_left;Node* cur_right = cur->_right;int CR_bf = cur_right->_bf;RotateL(cur);RotateR(parent);if (CR_bf == 0){parent->_bf = cur->_bf = cur_right->_bf = 0;}else if(CR_bf == 1){cur->_bf = -1;parent->_bf = cur_right->_bf = 0;}else if (CR_bf == -1){parent->_bf = 1;cur->_bf = cur_right->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}void RotateRL(Node* parent){Node* cur = parent->_right;Node* cur_left = cur->_left;//CL——CurLeftint CL_bf = cur_left->_bf;RotateR(cur);RotateL(parent);if (CL_bf == 0){cur->_bf = parent->_bf = cur_left->_bf = 0;}else if (CL_bf == 1){parent->_bf = -1;cur->_bf = cur_left->_bf = 0;}else if(CL_bf == -1){cur->_bf = 1;parent->_bf = cur_left->_bf = 0;}else{cout << __LINE__ << ":" << endl;perror("平衡因子有误");exit(-1);}}void RotateL(Node* parent){//画图分析://操作的结点有cur,cur_left,ppnodeNode* cur = parent->_right;Node* cur_left = cur->_left;//将parent的右节点改为cur_leftparent->_right = cur_left;//改变cur_left父节点的转向//cur_left可能为空if (cur_left != nullptr){cur_left->_parent = parent;}//将parent链接在cur的左边//为了更新cur的parent需要保存parent的父节点Node* ppnode = parent->_parent;cur->_left = parent;parent->_parent = cur;//ppnode可能为空if (ppnode == nullptr){//需要修改根节点_root = cur;cur->_parent = nullptr;}else{//改变ppnode的指向if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}void RotateR(Node* parent){//操作的结点Node* cur = parent->_left;Node* cur_right = cur->_right;//第一步:将cur_right链接到parent的leftparent->_left = cur_right;//更改cur_right的父节点//注意:cur_right可能为空if (cur_right != nullptr){cur_right->_parent = parent;}//第二步:将parent链接到cur的右结点。//先保存一下parent的父节点Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;//ppnode为空说明需要修改根节点if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}//更新平衡因子cur->_bf = parent->_bf = 0;}Node* _root = nullptr;};
};总结
AVL树还有删除操作,等博主有空再补充,对于AVL树一般来说只需要弄懂一种单旋,一种双旋,再加一些细写处理,代码是不难的,难就难在了分类讨论+画图上。今天的分享就到这里了,如果感觉有所帮助,不妨点个赞鼓励一下吧!
相关文章:

【数据结构】AVL树的插入与验证
文章目录 一、基本概念1.发展背景2.性质 二、实现原理①插入操作1.平衡因子1.1平衡因子的更新1.1.1树的高度变化1.1.2树的高度不变 2. 旋转2.1左旋2.2右旋2.3右左双旋2.4 左右双旋 ②验证1.求二叉树高度2. 判断是否为AVL树 源码总结 一、基本概念 1.发展背景 普通的二叉搜索树…...

9.3.3网络原理(网络层IP)
一.报文: 1.4位版本号:IPv4和IPv6(其它可能是实验室版本). 2.4位首部长度:和TCP一样,可变长,带选项,单位是4字节. 3.8位服务类型 4.16位总长度:IP报头 IP载荷 传输层是不知道载荷长度的,需要网络层来计算. IP报文 - IP报头 IP载荷 TCP报文 TCP载荷 IP载荷(TCP报文) …...

代码随想录算法训练营第四十八天| LeetCode121. 买卖股票的最佳时机、122.买卖股票的最佳时机II、123.买卖股票的最佳时机III
121. 买卖股票的最佳时机 题目描述: 121. 买卖股票的最佳时机. 解法 dp class Solution(object):def maxProfit(self, prices):if not prices:return 0dp0 0# 0表示不持有股票,1表示持有股票dp1 0-prices[0]for i in range(1,len(prices)):# 当前没有股票# 两…...

C++新经典10--vector以及其使用
vector vector类型是一个标准库中的类型,代表一个容器、集合或者动态数组这样一种概念。既然是容器,那就可以把若干个对象放到里面。当然,这些对象的类型必须相同。简单来说,可以把一堆int型数字放到vector容器中去,复…...

std : : vector
一.简介 std::vector 的底层实现通常基于动态数组(dynamic array),它是一种连续分配的内存块,允许元素的快速随机访问。下面是 std::vector 的一些关键特点和底层实现细节: 连续内存块:std::vector 内部使…...
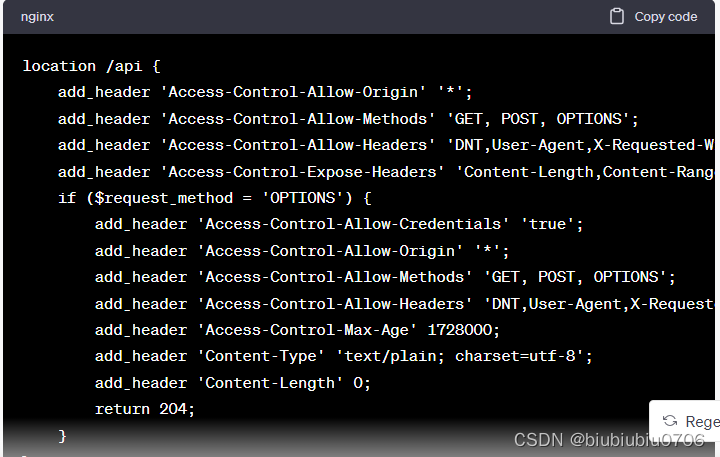
AJAX学习笔记8 跨域问题及解决方案
AJAX学习笔记7 AJAX实现省市联动_biubiubiu0706的博客-CSDN博客 跨域:指一个域名的网页去请求另外一个域名资源.比如百度页面去请求京东页面资源. 同源与不同源三要素:协议,域名,端口 协议一致,域名一致,端口一致.才算是同源.其他一律不同源 新建项目测试: 1.window.open();…...
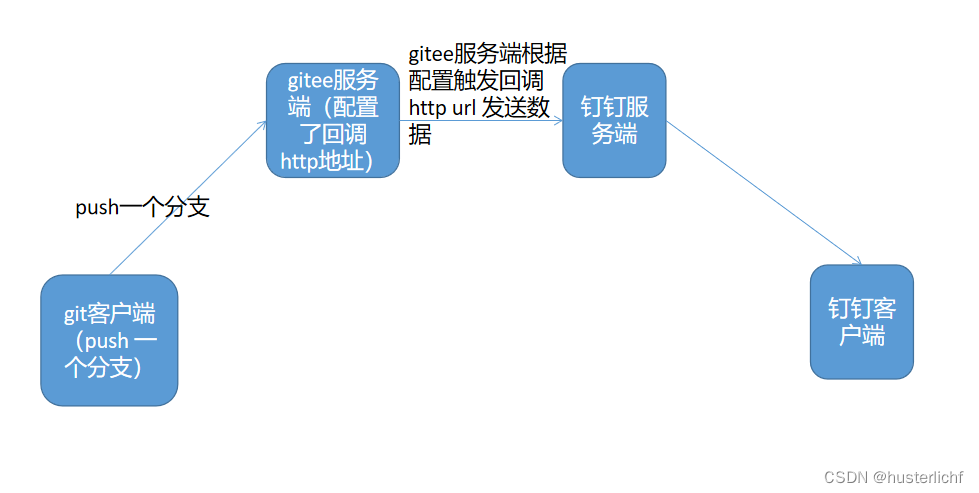
webhook--详解(gitee 推送)
一、简介 webhook 是一种基于 HTTP 的回调函数,可在 2 个应用编程接口(API)之间实现轻量级的事件驱动通信。是一种新型的前后端交互方式,一种对客户端-服务器模式的逆转,在传统方法中,客户端从服务器请求数…...
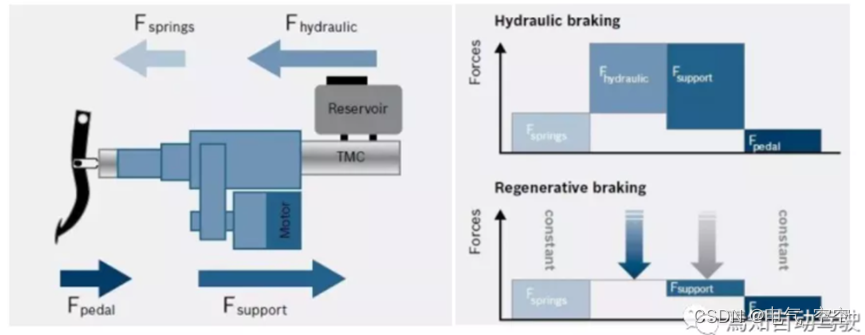
高速路自动驾驶功能HWP功能定义
一、功能定义 高速路自动驾驶功能HWP是指在一般畅通高速公路或城市快速路上驾驶员可以放开双手双脚,同时注意力可在较长时间内从驾驶环境中转移,做一些诸如看手机、接电话、看风景等活动,该系统最低工作速度为60kph。 如上两种不同环境和速度…...

Leetcode113. 路径总和 II
力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。 官方题解:力扣(LeetCode)官网 - 全…...

分布式锁之redis实现
docker安装redis 拉取镜像 docker pull redis:6.2.6 查看镜像 启动容器并挂载目录 需要挂在的data和redis.conf自行创建即可 docker run --restart always -d -v /usr/local/docker/redis/redis.conf:/usr/local/etc/redis/redis.conf -v /usr/local/docker/redis/data:/dat…...
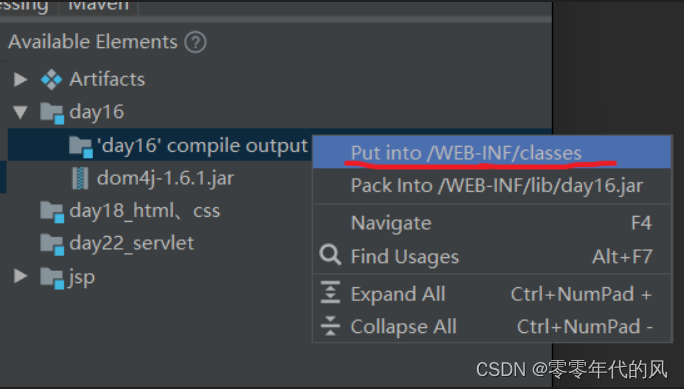
Idea中如何在一个项目中引入其他子模块?
首先在Settings打开Project Structure,然后找到Modules,点击加号点击import module,将需要引进的module引进来。 然后点击Artifacts 可以看到比如说day22…这个是我现在的项目,day16是我需要引入的。那么就在红色横线上面右键点第…...

UDP协议概述
传输层里比较重要的两个协议,一个是 TCP,一个是 UDP。TCP 是面向连接的,UDP 是面向无连接的。 所谓的建立连接,是为了在客户端和服务端维护连接,而建立一定的数据结构来维护双方交互的状态,用这样的数据结…...

Python-tracemalloc-跟踪内存分配
tracemalloc 模块是一个用于对 python 已申请的内存块进行debug的工具。它能提供以下信息: 定位对象分配内存的位置 按文件、按行统计python的内存块分配情况: 总大小、块的数量以及块平均大小。 对比两个内存快照的差异,以便排查内存泄漏 显示前10项 显示内存…...

02 CSS技巧
02 CSS技巧 clip-path 自定义形状,或者使用自带的属性画圆等circle HTML结构 <body><div class"container"></div> </body>CSS结构 使用*polygon*自定义形状 .container {width: 300px;height: 300px;background-color: re…...

Yarn资源调度器
文章目录 一、Yarn资源调度器1、架构2、Yarn工作机制3、HDFS、YARN、MR关系4、作业提交之HDFS&MapReduce 二、Yarn调度器和调度算法1、先进先出调度器(FIFO)2、容量调度器(Capacity Scheduler)3、公平调度器(Fair …...
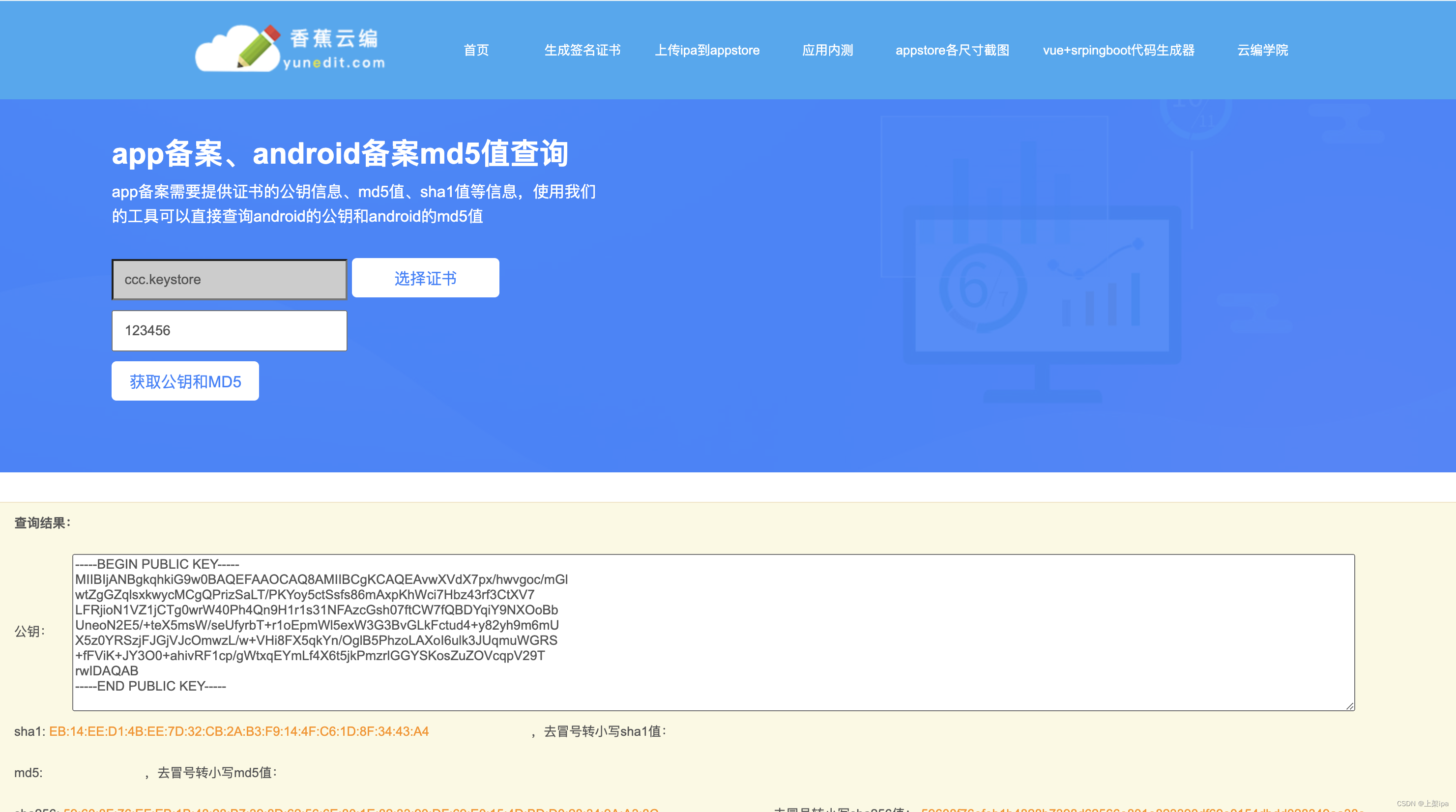
android上架备案公钥和md5获取工具
最近很多公司上架遇到了一个问题,就是要提供app的备案证明,现在android上架都需要备案了,但是我们的证书都是通过工具生成的,哪里知道公钥和md5那些东西呢?无论安卓备案还是ios备案都需要提供公钥和md5。 包括ios的备案…...
SpringBoot系列(12):SpringBoot集成log4j2日志配置
最近项目上有使用到log4j2日志模板配置,本文简单总结一下之前的学习笔记,如有纰漏之处,请批评指正。 1. log4j2日志依赖 使用log4j2日志模板时,需要引入相关依赖,下边的两种依赖方式均可。 1.1 使用sl4j依赖时 <…...

HTML事件列表
鼠标事件 属性描述DOMonclick当用户点击某个对象时调用的事件句柄。2oncontextmenu在用户点击鼠标右键打开上下文菜单时触发ondblclick当用户双击某个对象时调用的事件句柄。2onmousedown鼠标按钮被按下。2onmouseenter当鼠标指针移动到元素上时触发。2onmouseleave当鼠标指针…...
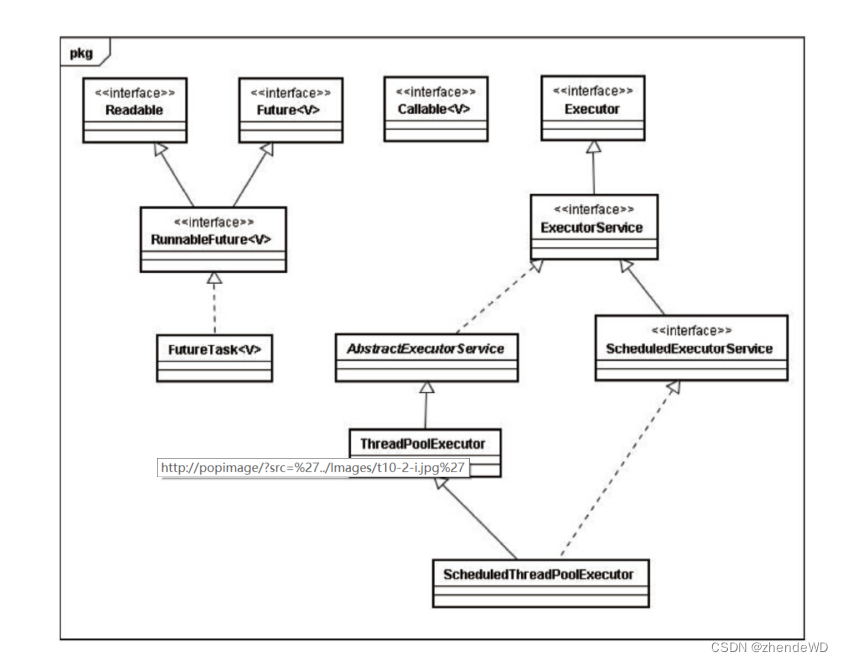
并发-Executor框架笔记
Executor框架 jdk5开始,把工作单元与执行机制分离开来,工作单元包括Runable和Callable,执行机制由Executor框架来提供。 Executor框架简介 Executor框架的两级调度模型 Java线程被一对一映射为本地操作系统线程 java线程启动会创建一个本…...
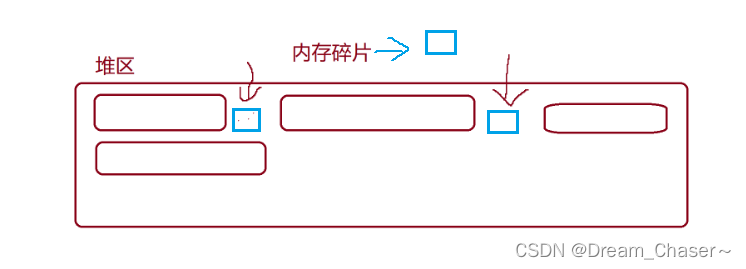
【C进阶】分析 C/C++程序的内存开辟与柔性数组(内有干货)
前言: 本文是对于动态内存管理知识后续的补充,以及加深对其的理解。对于动态内存管理涉及的大部分知识在这篇文章中 ---- 【C进阶】 动态内存管理_Dream_Chaser~的博客-CSDN博客 本文涉及的知识内容主要在两方面: 简单解析C/C程序…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...
