LASSO回归
LASSO回归
LASSO(Least Absolute Shrinkage and Selection Operator,最小绝对值收敛和选择算子算法)是一种回归分析技术,用于变量选择和正则化。它由Robert Tibshirani于1996年提出,作为传统最小二乘回归方法的替代品。
损失函数
1.线性回归
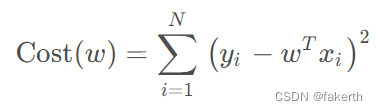
2.岭回归
岭回归的损失函数,在标准线性回归损失函数的基础上,增加了对权重的控制,作为正则化项,惩罚系λ乘以w向量的L2-范数的平方。
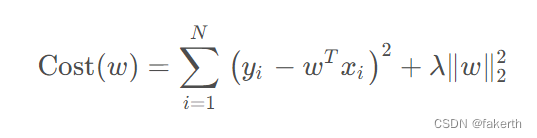
3.LASSO回归
LASSO回归的损失函数,同样在标准线性回归损失函数的基础上,增加了正则化项,正则化项改为惩罚系数λ乘以w向量的L1-范数的平方。
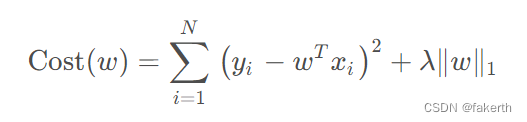
岭回归和LASSO回归通过调节λ的值来控制正则化的强度。λ的值越大,收缩效果越明显,越多的预测变量系数被设为零。相反,λ的值越小,模型越不稀疏,允许更多的预测变量具有非零系数。较小的λ值会接近于普通最小二乘回归。
在LASSO回归中,由于L1范数的几何特性,导致某些参数估计值为零,从而实现了变量的稀疏性。而岭回归通常会使得参数估计值接近于零,但不会精确地将某些参数收缩到零。
由于LASSO损失函数存在绝对值,所以并不是处处可导的,所以没办法通过直接求导的方式来直接得到w。
坐标下降法
坐标下降法(Coordinate Descent)是一种优化算法,用于求解无约束优化问题。它适用于目标函数可分解为各个变量的子问题的情况,即目标函数可以表示为各个变量的函数的和。
坐标下降法的基本思想是,在每次迭代中,固定除一个变量以外的其他变量,通过求解仅关于该变量的子问题来更新该变量的值。然后依次对每个变量进行更新,直到满足停止准则或达到最大迭代次数。坐标下降法的迭代步骤如下:
-
1.初始化变量的初始值。
-
2.选择一个变量wi。
-
3.将除变量wi以外的其他变量固定,将目标函数表示为只关于变量wi的函数。
-
4.求解子问题,更新变量wi的值,使得目标函数最小化。
-
5.重复步骤2-4,对下一个变量进行更新,直到所有变量都被更新一遍。
-
6.检查停止准则(当所有权重系数的变化不大或者到达最大迭代次数时,结束迭代
),如果满足停止准则,则停止迭代;否则返回步骤2。
在第k次迭代时,更新权重系数的方法如下:

最小角回归
-
1.初始化:将所有自变量的系数设为零。
-
2.计算残差:计算当前模型的残差向量,表示目标变量与当前模型预测之间的差异。
-
3.选择自变量:选择与残差向量具有最大相关性的自变量。可以使用内积或相关系数来度量相关性。在初始阶段,与残差具有最大相关性的自变量将被选为第一个加入模型的自变量。
-
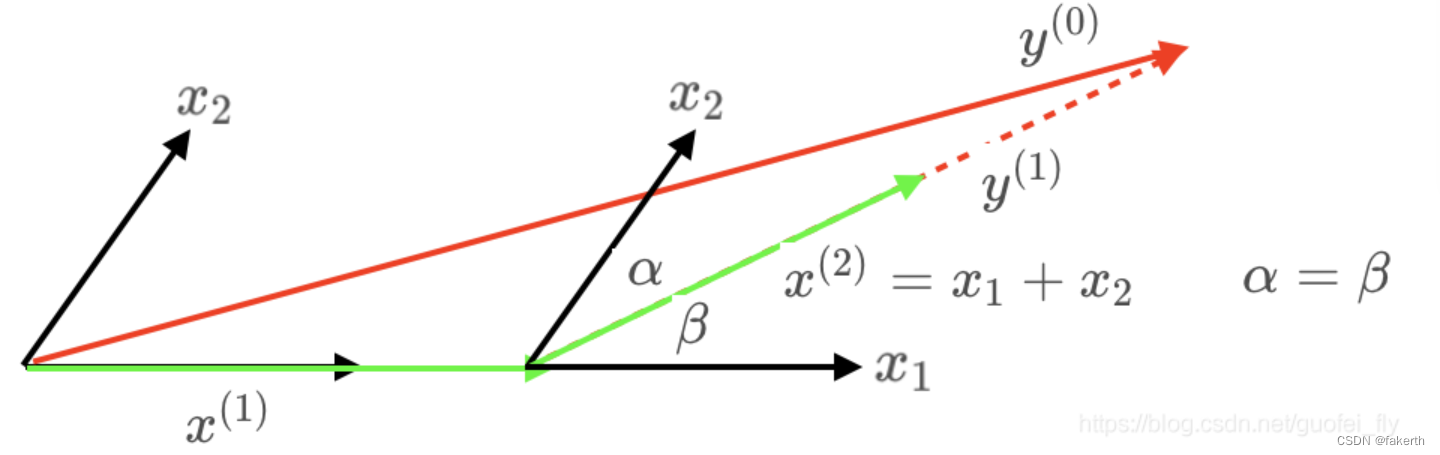
4.移动向量:将当前自变量的系数朝着它与残差向量之间的夹角最小的方向移动。这可以通过计算自变量与残差向量的内积来实现。
-
5.跟踪相关性:跟踪已选定自变量与其他自变量之间的相关性变化。为此,计算每个自变量与残差向量之间的相关系数。
-
6.更新系数:根据相关性的变化,更新自变量的系数。具体而言,增加具有最大相关系数的自变量的系数,使其逐渐接近其最终值。
-
7.跟踪变量:在更新系数后,重新计算已选定自变量与其他自变量之间的相关系数,以跟踪相关性的变化。
-
8.重复步骤4-7:重复移动向量、跟踪相关性和更新系数的步骤,直到选择的自变量数达到预设的阈值或满足其他停止准则。停止准则可以是预先确定的自变量数目,也可以是基于交叉验证或信息准则的模型选择方法。
sklearn实现
1.坐标下降法
from sklearn.linear_model import Lasso# 初始化Lasso回归器,默认使用坐标下降法
reg = Lasso(alpha=0.1, fit_intercept=False)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_2.最小角回归法
from sklearn.linear_model import LassoLars# 初始化Lasso回归器,使用最小角回归法
reg = LassoLars(alpha=0.1, fit_intercept=False)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_参考:机器学习算法系列-Lasso回归算法
相关文章:

LASSO回归
LASSO回归 LASSO(Least Absolute Shrinkage and Selection Operator,最小绝对值收敛和选择算子算法)是一种回归分析技术,用于变量选择和正则化。它由Robert Tibshirani于1996年提出,作为传统最小二乘回归方法的替代品。 损失函数 1.线性回…...

机器学习中的 K-均值聚类算法及其优缺点。
K-均值聚类算法是一种常见的无监督学习算法,它可以将数据集分成 K 个簇,每个簇内部的数据点尽可能相似,而不同簇之间的数据点应尽可能不同。下面详细讲解 K-均值聚类算法的优缺点: 优点: 简单易用:K-均值…...
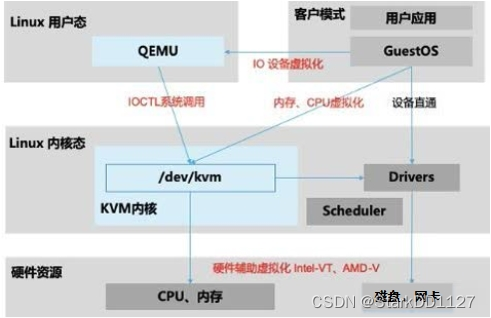
云计算与虚拟化
一、概念 什么是云计算? 云计算(cloud computing)是分布式计算的一种,指的是通过网络“云”将巨大的数据计算处理程序分解成无数个小程序,然后,通过多部服务器组成的系统进行处理和分析这些小程序得到结果…...

Linux常见进程类别
目录 常见进程类别 守护进程&精灵进程 任务管理 进程组 作业 作业 | 进程组 会话 w命令 守护进程 守护进程的创建 setsid()函数 daemon()函数 模拟实现daemon函数 前台进程 | 后台进程 僵尸进程 | 孤儿进程 僵尸进程的一些细节 守护进程 | 后台进程 守护…...

智能小车之蓝牙控制并测速小车、wife控制小车、4g控制小车、语音控制小车
目录 1. 蓝牙控制小车 2. 蓝牙控制并测速小车 3. wifi控制测速小车 4. 4g控制小车 5. 语音控制小车 1. 蓝牙控制小车 使用蓝牙模块,串口透传蓝牙模块,又叫做蓝牙串口模块 串口透传技术: 透传即透明传送,是指在数据的传输过…...
指针进阶(一)
指针进阶 1. 字符指针面试题 2. 指针数组3. 数组指针3.1 数组指针的定义3.2 &数组名VS数组名 3.3 数组指针的使用4. 数组传参和指针传参4.1 一维数组传参4.2 二维数组传参4.3 一级指针传参4.4 二级指针传参 前言 指针的主题,我们在初级阶段的《指针》章节已经接…...

c# sql 判断表中是否包含指定字段
你可以使用以下方法来判断一个 SQL 数据库中的表是否包含指定的字段。 首先,你需要连接到数据库,然后执行一条 SQL 查询语句来检查表结构。你可以使用 SELECT 语句和 INFORMATION_SCHEMA.COLUMNS 系统视图来获取表中的所有列信息。 下面是一个示例代码…...

08-JVM垃圾收集器详解
上一篇:07-垃圾收集算法详解 如果说收集算法是内存回收的方法论,那么垃圾收集器就是内存回收的具体实现。 虽然我们对各个收集器进行比较,但并非为了挑选出一个最好的收集器。因为直到现在为止还没有最好的垃圾收集器出现,更加没…...
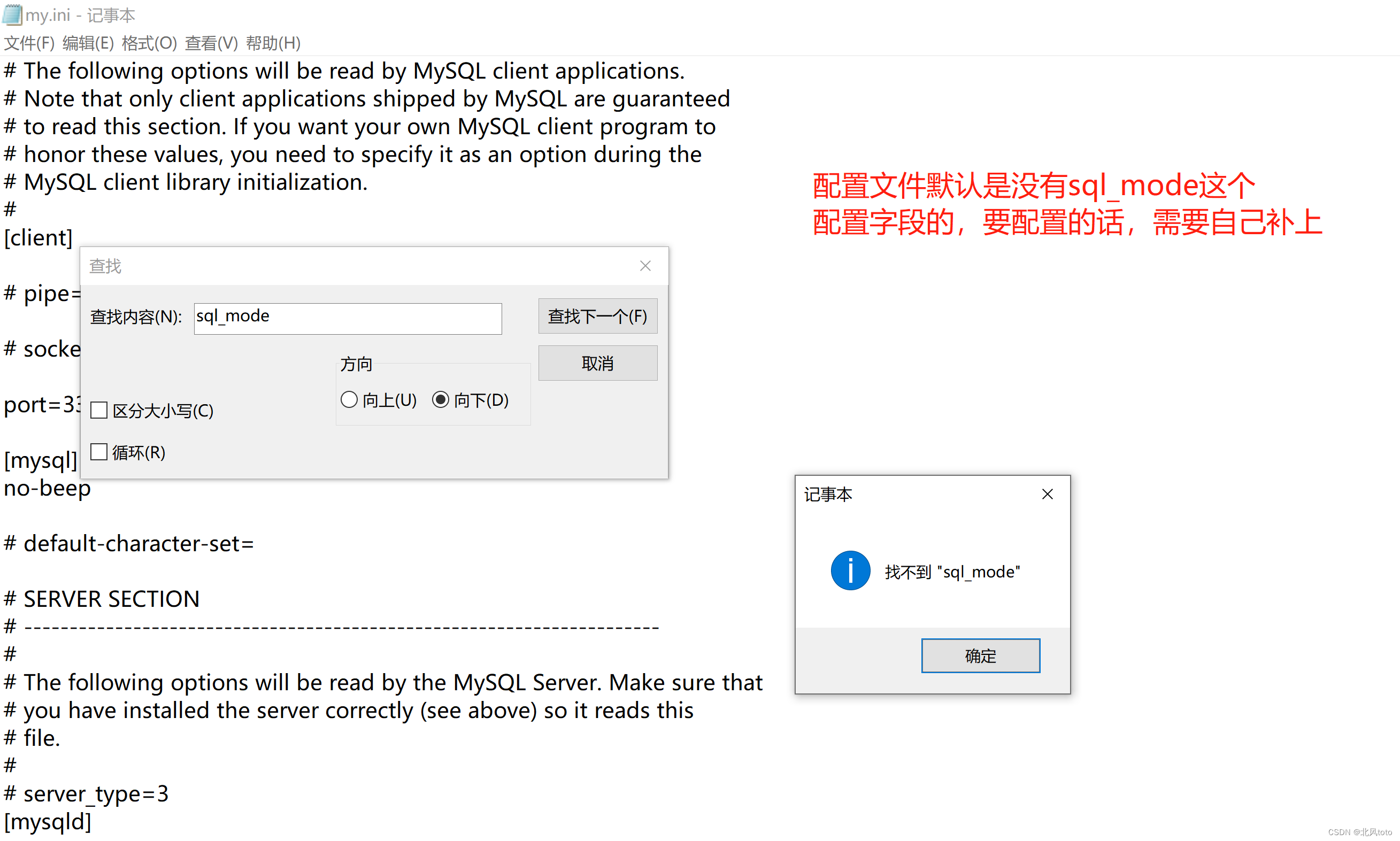
sql_mode详解
文章目录 一、sql_mode作用二、查询sql_mode三、mysql8默认的mode配置(6个默认配置)四、常见mode详细解释mysql8默认配置了的mode(6个)需要自己配置的mode(4个) 五、设置sql_mode(一旦设置了&am…...

Vue3的新特性总结
一、Vue3 里 script 的三种写法 首先,Vue3 新增了一个叫做组合式 api 的东西,英文名叫 Composition API。因此 Vue3 的 script 现在支持三种写法。 1、最基本的 Vue2 写法 <template><div>{{ count }}</div><button click"…...

【Node】Mac多版本Node切换
1、查看当前电脑是否安装node node -v或者查看当前电脑通过brew安装的node路径 ls /usr/local/Cellar/node*2、查看可安装的node brew search node3、安装其他版本node 下载需要安装的node版本 brew install node144、brew切换node版本 假设之前的版本是18,需…...

Apache POI
POI介绍 Apache POI是用Java编写的免费开源的跨平台的Java API, Apache POI提供API给Java程序对Microsoft Office格式档案读和写的功能, 其中使用最多的就是使用POI操作Excel文件。 maven坐标: <dependency><groupId>org.apa…...

个人能做股票期权吗?个人期权交易开户条件新规
个人投资者是可以交易股票期权的,不过期权交易通常需要投资者具备一定的投资经验和风险承受能力,因为期权交易涉及较高的风险和复杂性,下文为大家介绍个人能做股票期权吗?个人期权交易开户条件新规的内容。本文来自:期…...
)
Java面试整理(一)
开篇 面试,应该都是打工人需要面对的事情。我记得自己以前开始准备Java工程师面试时,都会去看那个《面试宝典》,当时这个“宝典”真的很经典,现在应该还是不少朋友会看这个。我自己经历过了找工作的面试,和企业招聘工作。所以我自己更加想从这两个不同的角度去和大家交流这…...
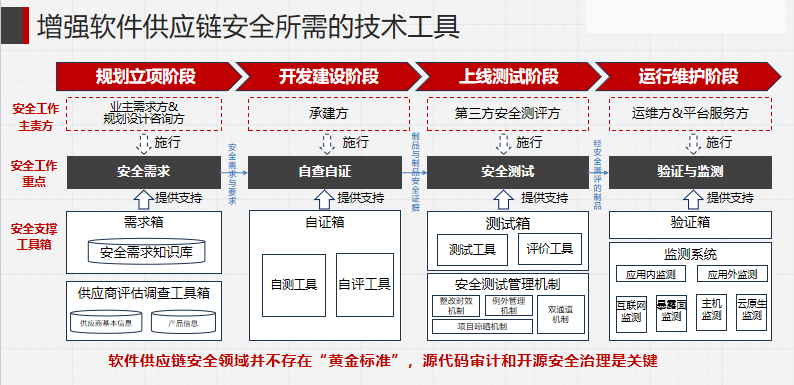
国家信息中心举办“数字政府建设暨数字安全技术”研讨会:海云安提出数字政府软件供应链安全解决方案
近日,由国家信息中心主办,复旦大学研究院承办的“数字政府建设暨数字安全技术研讨会”在义乌顺利召开。国家信息中心信息与网络安全部副主任禄凯,复旦大学党委常委、宣传部部长陈玉刚,义乌市委常委、常务副市长喻新贵为会议致辞。…...
uniapp 处理 分页请求
我的需求是手机上一个动态滚动列表,下拉到底部时,触发分页数据请求 uniapp上处理分页解决方案 主要看你是如何写出滚动条的。我想到的目前有三种 (1)页面滚动:直接使用onReachBottom方法,可以监听到达底部…...

最新2米分辨率北极开源DEM数据集(矢量文件)
一、项目背景 美国明尼苏达大学(University of Minnesota)的极地地理空间中心(Polar Geospatial Center, PGC)于2023年8月发布了北极数字高程模型4.1版本(ArcticDEM Mosaic 4.1)。该DEM数据集是革命性的,分辨率达到了2米,而一般的开源DEM数据集分辨率是3…...
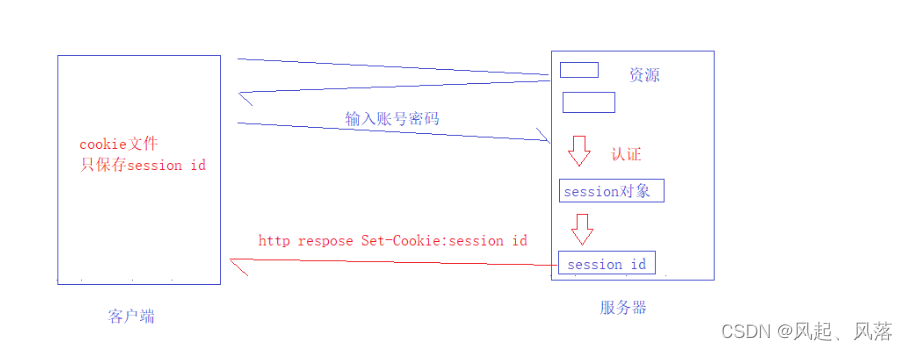
【计算机网络】HTTP(下)
本文承接上文的代码进行改造,上文链接:HTTP上 文章目录 1. 实现网站跳转实现 自己的网站跳转 2. 请求方法(get) && 响应方法(post)GET方法POST方法GET与POST的应用场景 3. HTTP状态码在自己设计的代码中发现4043开头的状态码(重定向状态码)永久…...

自学Python03-学会Python中的while循环语句
我们来学习一下怎么使用列表和字典吧! 1.列表 首先,我们来学习一下列表。列表是一个有序的集合,它可以包含任何类型的数据,比如数字、字符串或其他列表。我们可以用方括号 [] 来创建一个列表,用逗号分隔各个元素。 …...
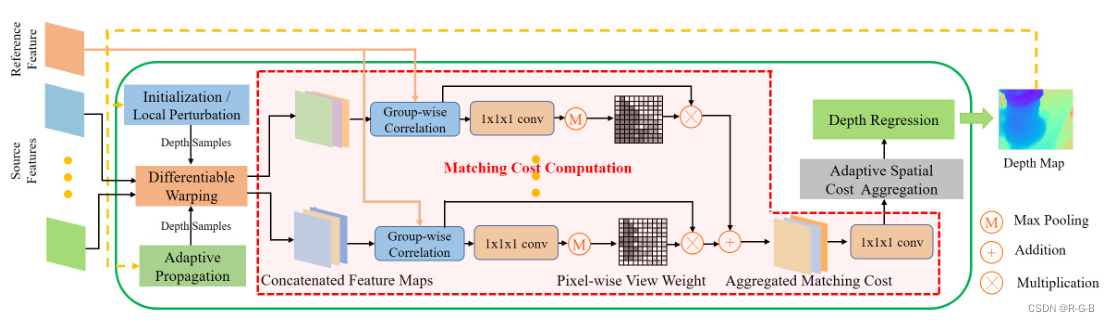
PatchMatchNet 学习笔记 译文 深度学习三维重建
9 PatchMatchNet CVPR-2021 patchmatchnet源码下载 PatchMatchNet 代码注释版 下载链接(注释非常详细,较源码结构有调整,使用起来更方便) PatchMatchNet-CVPR-2021(源码、原文+注释+译文+批注) 9.0 主要特点 金字塔,基于传统的PatchMatch算法,精度高,速度快 Pa…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
