2023年数维杯数学建模A题河流-地下水系统水体污染研求解全过程文档及程序
2023年数维杯数学建模
A题 河流-地下水系统水体污染研
原题再现:
河流对地下水有着直接地影响,当河流补给地下水时,河流一旦被污染,容易导致地下水以及紧依河流分布的傍河水源地将受到不同程度的污染,这将严重影响工农业的正常运作、社会经济的发展和饮水安全。在地下水污染中最难治理和危害最大的是有机污染,因而对有机污染物在河流-地下水系统中的行为特征进行研究具有十分重要的理论意义和实际价值。另外,已有研究表明在河流地下水系统中有机污染物的行为特征主要涉及对流迁移、水动力弥散、吸附及阻滞等物理过程、化学反应过程以及生物转化过程等。现设地下水渗流场为各向同性均质的稳态流,对有机污染物的迁移和转化规律进行研究和探索,并完成以下问题。
问题1 通过查阅相关文献和资料,分析并建立河流-地下水系统中有机污染物的对流、弥散及吸附作用的数学模型 。
问题2 试利用下面介绍的内容和表中试验参数以及数据依据数学模型研究某有机污染物在河流-地下水系统中的迁移转化机理。
1) 对流、弥散试验参数
通过试验测得河流-地下水系统中某有机污染物的对流、弥散有关参数见表1。

2)吸附动力学试验结果
四种不同河流沉积物对初始浓度为0.5mg/L左右的某有机污染物吸附体系的吸附动力学过程及不同吸附时间测得固、液相某有机物的浓度列于表2中.
3)等温平衡吸附试验结果
地下水中有机污染物的吸附行为采用等温平衡吸附的数学模型描述,四种不同沉积物对10种不同初始浓度的某有机污染物24小时的等温平衡吸附试验结果列于表3中.
问题3 生物降解是污染物一个很重要的转化过程,考虑生物降解作用对有机污染物转化的影响,建立适当的数学模型,试结合表4中的试验数据分析微生物对该有机污染物的降解特性。
整体求解过程概述(摘要)
党的二十大报告指出,“深入推进环境污染防治,统筹水资源、水环境、水生态治理,推动重要江河湖库生态保护治理,基本消除城市黑臭水体”。其中河流和地下水系统在人类生活中发挥关键作用。当污染发生时,河流对地下水的补给可能导致周边水源受污,影响工农业运作、社会发展及饮水安全。在地下水污染中,有机污染物的问题最为棘手。为了解这类污染物在河流-地下水系统中的行为,我们需要深入研究其物理、化学反应和生物转化过程。本研究将以各向同性均质的稳态流作为地下水渗流场,探究有机污染物的迁移与转化规律。
对于问题一,我们查阅相关文献资料分别得出对流方程、弥散方程以及吸附作用方程。我们将基于质量守恒方程与一些假设条件,建立描述有机污染物浓度变化的一维及多维对流-弥散-吸附微分方程,接着通过有限差分法求解该一维微分方程,以便直观地观察模型参数对有机污染物迁移转化过程的影响。
对于问题二,我们将基于给定的四种有机物液、固相实验数据,对模型进行参数调整和检验。首先,基于对流、弥散试验参数,更新微分方程的模型参数,以更准确地描述有机污染物的迁移转化过程;然后,根据四种不同河流沉积物的吸附动力学数据,重新计算吸附系数k值,由于给定的时间数据比较离散,本文使用插值方法进行数值模拟,将更新后的k值用于微分方程求解;最后,基于四种有机物液、固相状态下的初始浓度与平衡浓度数据,通过匹配对可以迭代计算出初始浓度与等温吸附24小时后平衡的浓度的吸附系数k值。然后求均值作为吸附系数k,更新微分方程模型参数。
对于问题三,我们将在微分方程模型中引入生物降解过程,以研究微生物对有机污染物的降解特性,假设生物降解速率与微生物浓度M和有机物浓度C之间存在线性关系,则可在原有的对流弥散-吸附模型中添加生物降解项,形成新的数学模型一对流-弥散-吸附-生物降解的微分方程。
问题分析:
问题1要求我们从已有的相关理论研究和实证分析中找到适用于本题的数学模型,用以描述河流-地下水系统中有机污染物的对流、弥散及吸附作用。由于团队相关专业知识的了解程度较低,我们决定将问题简化,建立描述河流-地下水系统中有机污染物变化的一维对流—弥散—吸附微分方程,并通过有限差分法求解该方程,以便能够直观地呈现出模型参数对有机物污染物迁移转化过程的影响,同时有利于求解问题2。
对于第二个问题,我们将基于给定的实验数据,对模型进行参数调整和验证。首先,我们将优化微分方程的模型参数,以更准确地描述有机污染物的迁移转化过程。然后,我们将根据四种不同河流沉淀物的吸附动力学数据, 重新计算吸附系数k 值。由于给定的时间数据比较离散,我们将考虑结合插值方法进行数值模拟,最后,我们将对每种有机物在不同状态下的浓度变化情况进行模拟,以验证我们的模型和参数调整的有效性。
对于第三个问题,我们将在微分方程模型中引入生物降解过程,以研究微生物对有机污染物的降解特性。具体地,我们将在原有的对流-弥散-吸附模型中添加生物降解项,形成新的数学模型。然后,我们将根据河流等温平衡吸附24小时后的浓度变化数据,通过迭代计算方法求解吸附系数k值。最后,我们将求得的k值的均值作为新模型的吸附系数k,以此来更新我们的数学模型。
模型假设:
1.一维空间假设:将河流-地下水系统近似为一维空间,忽略横向扩散和纵向非均匀性;
2.连续性假设:假设有机污染物的浓度分布在空间上具有一定的连续性和平滑性,可以用微分方程来描述;
3.线性生物降解假设:假设生物降解速率与微生物浓度和有机物浓度之间存在线性关系,用生物降解速率常数上表示;
4.稳态吸附假设:假设吸附过程处于稳态,吸附系数k不随时间变化;
5.地下水流速相对于孔隙流速u来说较小,因此可以忽略其对流的影响。
论文缩略图:



全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
程序代码:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"]
plt.rcParams["axes.unicode_minus"]=False
for dd in range(1,13,3):
# 模型参数
L = 100 # 系统长度(单位:m)
Nx = 24 # 空间离散化点数
T = 24 # 模拟时间(单位:天)
Nt = 1000 # 时间离散化步数
dx = L / (Nx - 1) # 空间步长
dt = T / Nt # 时间步长
v = 0.1 # 水流速度(单位:m/day)
D = 0.01 # 弥散系数(单位:m²/day)
k = 0.001 # 吸附系数(单位:1/day)
# 初始条件
C0 = np.zeros(Nx) # 初始浓度分布
C0[int(Nx / 2)] =dd # 在中心位置设置初始浓度为1.0
# 数值求解
C = np.zeros((Nt, Nx)) # 存储浓度分布的数组
C[0, :] = C0
for t in range(1, Nt)
for x in range(1, Nx - 1):
# 对流项
convective = -v * (C[t-1, x] - C[t-1, x-1]) / dx
# 弥散项
dispersive = D * (C[t-1, x+1] - 2 * C[t-1, x] + C[t-1, x-1]) / (dx**2)
# 吸附项
adsorption = -k * C[t-1, x]
# 数值更新
C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption)
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
X, T = np.meshgrid(x, t)
plt.contourf(X, T, C, cmap='cool')
plt.colorbar(label='浓度')
plt.xlabel('距离 (m)')
plt.ylabel('天数 (days)')
plt.title('浓度为%s_污染物浓度'%dd)
plt.savefig('./Q1/浓度为%s_污染物浓度.jpg'%dd)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.pyplot as plt
plt.rcParams["font.sans-serif"]=["SimHei"]
plt.rcParams["axes.unicode_minus"]=False
for dd in range(1,13,3):
# 模型参数
L = 100 # 系统长度(单位:m)
Nx = 24 # 空间离散化点数
T = 24 # 模拟时间(单位:天)
Nt = 1000
dx = L / (Nx - 1) # 空间步长
dt = T / Nt # 时间步长
v = 0.1 # 水流速度(单位:m/day)
D = 0.01 # 弥散系数(单位:m²/day)
k = 0.001 # 吸附系数(单位:1/day)
# 初始条件
C0 = np.zeros(Nx) # 初始浓度分布
C0[int(Nx / 2)] =dd # 在中心位置设置初始浓度为1.0
# 数值求解
C = np.zeros((Nt, Nx)) # 存储浓度分布的数组
C[0, :] = C0
for t in range(1, Nt):
for x in range(1, Nx - 1):
# 对流项
convective = -v * (C[t-1, x] - C[t-1, x-1]) / dx
# 弥散项
dispersive = D * (C[t-1, x+1] - 2 * C[t-1, x] + C[t-1, x-1]) / (dx**2)
# 吸附项
adsorption = -k * C[t-1, x]
# 数值更新
C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption)
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
X, T = np.meshgrid(x, t)
fig = plt.figure(figsize=(10,10))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, T, C, cmap='viridis')
ax.set_xlabel('距离 (m)')
ax.set_ylabel('天数 (days)')
ax.set_zlabel('浓度')
ax.set_title('浓度为%s_污染物浓度' % dd)
plt.savefig('./Q2_1/_浓度为%s_污染物浓度.jpg' % dd)
plt.show()
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
plt.rcParams['font.sans-serif'] = ['STSong']
plt.rcParams['axes.unicode_minus'] = False
# 创建数据集
data3 = pd.DataFrame({
'初始浓度': [0.0681, 0.1372, 0.2177, 0.3302, 0.4324, 0.5338, 0.5842, 0.6222, 0.7062, 0.7956],
'S1液相': [0.0461, 0.0722, 0.1235, 0.2150, 0.2951, 0.3716, 0.3969, 0.4547, 0.4852, 0.5714],
'S1固相': [0.1702, 0.6005, 0.8921, 1.102, 1.323, 1.572, 1.823, 2.100, 2.160, 2.192],
'S2液相': [0.0246, 0.0492, 0.0903, 0.1725, 0.2563, 0.3376, 0.3574, 0.3701, 0.4352, 0.5043],
'S2固相': [0.1852, 0.8301, 1.224, 1.527, 1.711, 1.912, 2.218, 2.471, 2.660, 2.863],
'S3液相': [0.0424, 0.0654, 0.1091, 0.2068, 0.2614, 0.3304, 0.3852, 0.4065, 0.4467, 0.5999],
'S3固相': [0.2071, 0.6683, 1.036, 1.184, 1.660, 1.984, 1.940, 2.107, 2.545, 2.937],
'S4液相': [0.0354, 0.0613, 0.0993, 0.1931, 0.2528, 0.2879, 0.3568, 0.4195, 0.5071, 0.5061],
'S4固相': [0.2772, 0.7101, 1.134, 1.321, 1.546, 1.781, 2.124, 1.977, 2.461, 2.845]
})
# 创建数据集
data4 = pd.DataFrame({
'浓度': [0.483, 0.479, 0.452, 0.418, 0.371, 0.342, 0.319, 0.311, 0.309],
'微生物浓度': [1.50E+07, 1.70E+07, 2.00E+07, 2.50E+07, 3.00E+07, 3.30E+07, 3.50E+07, 3.70E+07, 3.70E+07],
'有机物浓度比': [1, 0.991718427, 0.935817805, 0.865424431, 0.768115942, 0.708074534, 0.660455487, 0.64389234, 0.639751553],
'天数': [0, 1, 2, 3, 4, 5, 6, 7, 8]
})
from scipy.interpolate import interp1d
for ii in data3.columns[1:]:
# 模型参数
L = 100 # 系统长度(单位:m)
Nx = 24 # 空间离散化点数
T = 24 # 模拟时间(单位:天)
Nt = 1000 # 时间离散化步数
dx = L / (Nx - 1) # 空间步长
dt = T / Nt # 时间步长
# 河流-地下水参数
u = 38.67 * 0.01 # 平均孔隙流速(单位:m/day),将单位转换为cm/d
ν = 5.01 * 0.01 # 地下水渗流流速(单位:m/day),将单位转换为cm/d
D = 0.38 * (1 / 1440) * 0.01**2 # 弥散系数(单位:cm²/min 转换为 m²/d)
k = 6.32 * 0.01 # 渗透系数(单位:m/day),将单位转换为cm/d
μ = 0.01 # 生物降解速率常数
# 含水层样品的干密度和孔隙度
ρ = 1.67 # 干密度(单位:g/cm³)
n = 0.375 # 孔隙度
print(ii)
temp=data3[['初始浓度',ii]]
k_list=[]
for i in range(temp.shape[0]):
# 计算吸附系数
C_max =temp.iloc[i,0] # 最大吸附浓度
Ce = temp.iloc[i,1] # 平衡浓度
k = C_max / (Ce - C_max) * (ρ * n)
k_list.append(k)
k=np.mean(k_list)
# 初始条件
C0 = np.zeros(Nx) # 初始浓度分布
C0[int(Nx / 2)] =0.483# 在中心位置设置初始浓度为1.0
# 数值求解
C = np.zeros((Nt, Nx)) # 存储浓度分布的数组
C[0, :] = C0
# 创建插值函数
# 时间插值
interp_func = interp1d(data4['天数'], data4['浓度'], kind='quadratic')
time_interp = np.linspace(0, T, Nt)
for t in range(1, Nt):
for x in range(1, Nx - 1):
# 对流项
convective = -(u + ν) * (C[t-1, x] - C[t-1, x-1]) / dx
# 弥散项
dispersive = D * (C[t-1, x+1] - 2 * C[t-1, x] + C[t-1, x-1]) / (dx**2)
# 吸附项
adsorption = -k * (ρ * n * C[t-1, x])
# 生物降解项
bio_degradation = -μ * C[t-1, x] * interp_func(np.clip([t * dt], 0, data4["浓
度"].iloc[-1]))
# 数值更新
C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption +
bio_degradation)
# # 数值更新
# C[t, x] = C[t-1, x] + dt * (convective + dispersive + adsorption)
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(T, 0, Nt)
if '固' in ii:
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(0, T, Nt)
else:
# 绘制浓度随时间和空间的分布图
x = np.linspace(0, L, Nx)
t = np.linspace(T, 0, Nt)
X, T = np.meshgrid(x, t)
plt.contourf(X, T, C, cmap='seismic')
plt.colorbar(label='浓度')
plt.xlabel('距离 (m)')
plt.ylabel('天数 (days)')
plt.title('%s 污染物浓度'%ii)
plt.savefig('./Q3/%s 污染物浓度.jpg'%ii)
plt.show()
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2023年数维杯数学建模A题河流-地下水系统水体污染研求解全过程文档及程序
2023年数维杯数学建模 A题 河流-地下水系统水体污染研 原题再现: 河流对地下水有着直接地影响,当河流补给地下水时,河流一旦被污染,容易导致地下水以及紧依河流分布的傍河水源地将受到不同程度的污染,这将严重影响工…...
Java测试(10)--- selenium
1.定位一组元素 (1)如何打开本地的HTML页面 拼成一个URL :file: /// 文件的绝对路径 import os os.path.abspath(文件的绝对路径) (2)先定位出同一类元素(tag name,name&…...

【文末送书】Matlab科学计算
欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。关…...

ElementUI浅尝辄止30:PageHeader 页头
如果页面的路径比较简单,推荐使用页头组件而非面包屑组件。 1.如何使用? <el-page-header back"goBack" content"详情页面"> </el-page-header><script>export default {methods: {goBack() {console.log(go bac…...

[Qt]基础数据类型和信号槽
文章目录 1. Qt基本结构1.1 Qt本有项目1.1.1 项目文件(.pro)1.1.2 main.cpp1.1.3 mainwindow.ui1.1.4 mainwindow.h1.1.5 mainwindow.cpp 1.2 Qt中的窗口类1.2.1基础窗口类1.2.2 窗口的显示 1.3 内存回收 2. Qt中的基础数据类型2.1 基础类型2.2 log输出2…...
UIStackView入门使用两个问题
项目中横向一排元素,竖向一排元素,可以使用UIStackView。UIStackView的原理不做介绍,这里主要讲两个初次使用容易出现的两个问题。 首先创建一个stackview -(UIStackView*)titleStackView{if(_titleStackView nil){_titleStackView [UISta…...
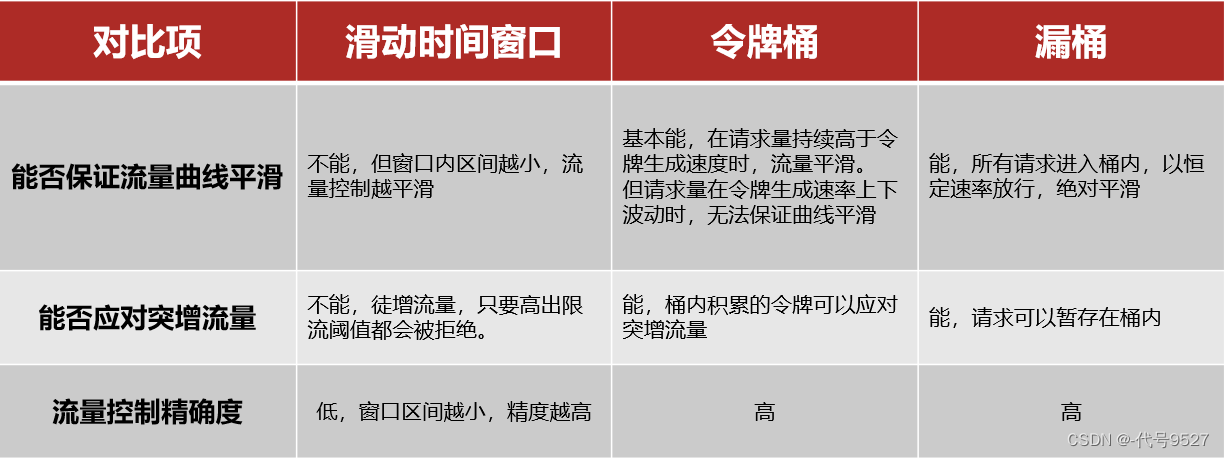
【Sentinel】Sentinel与gateway的限流算法
文章目录 1、Sentinel与Hystrix的区别2、限流算法3、限流算法对比4、Sentinel限流与Gateway限流 1、Sentinel与Hystrix的区别 线程隔离有两种方式实现: 线程池隔离(Hystrix默认采用)信号量隔离(Sentinel默认采用) 服…...
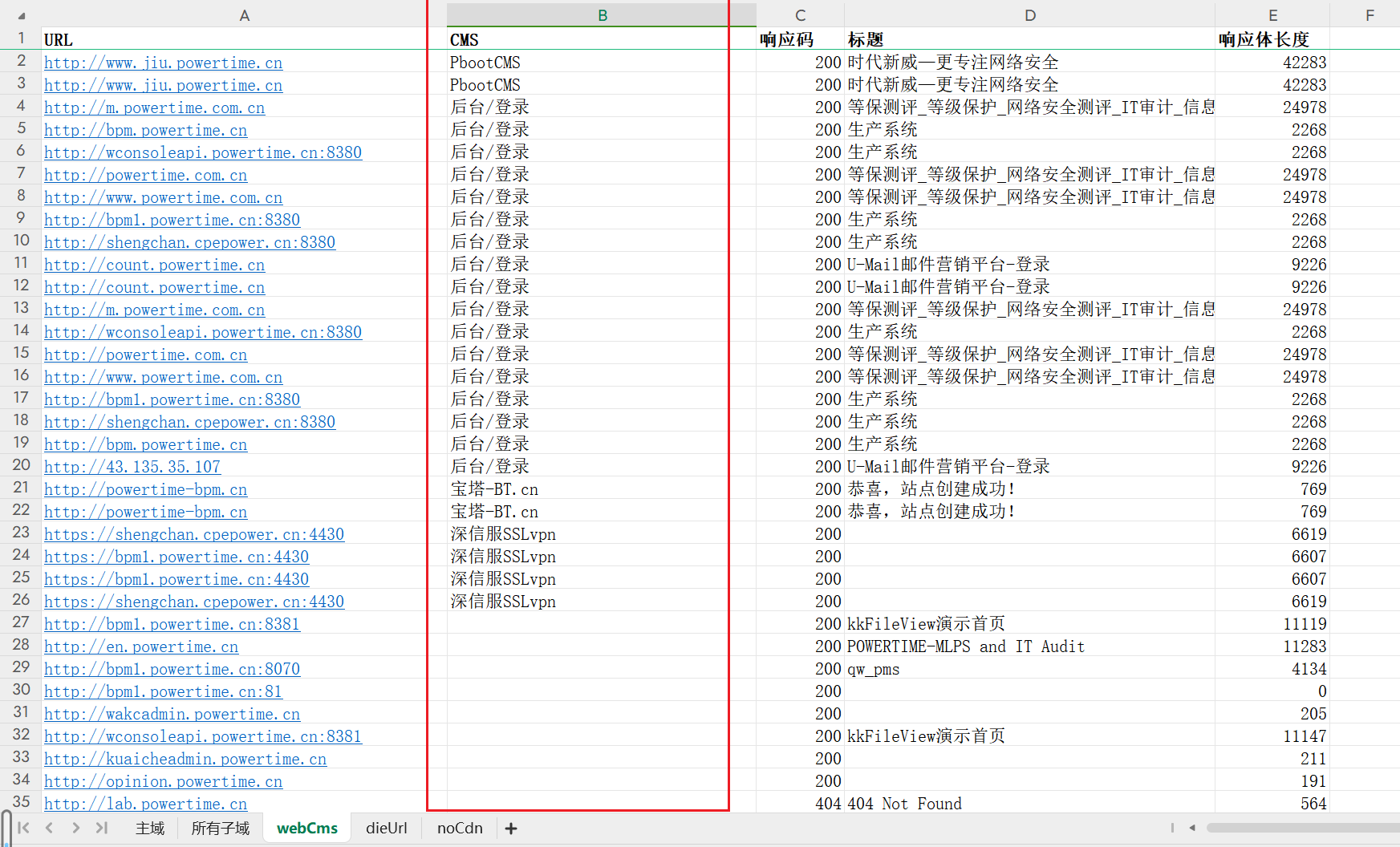
python实现对excel表中的某列数据进行排序
如下需要对webCms中的B列数据进行升序排序,且不能影响到其他列、工作表中的数据和格式。 import pandas as pd import openpyxl from openpyxl.utils.dataframe import dataframe_to_rows# 读取 Excel 文件 file_path 1.xlsx sheet_name webCms# 读取 Excel 文件并…...

CMS指纹识别
一.什么是指纹识别 常见cms系统 通过关键特征,识别出目标的CMS系统,服务器,开发语言,操作系统,CDN,WAF的类别版本等等 1.识别对象 1.CMS信息:比如Discuz,织梦,帝国CMS࿰…...

STL- 常用算法
概述: 算法主要是由头文件<algorithm> <functional> <numeric>组成。 <algorithm>是所有STL头文件中最大的一个,范围涉及到比较、 交换、查找、遍历操作、复制、修改等等 <numeric>体积很小,只包括几个在序列上面进行简…...
苹果铃声怎么设置?3招教你设置个性化铃声!
苹果手机因其颜值、性能与生态吸引了一大批粉丝用户。在拿到新手机后,大家第一时间就是给手机设置好听的铃声。那么,苹果铃声怎么设置呢?手机铃声能设置成自己喜欢的歌曲吗?当然可以了!本文将给大家介绍3种轻松设置苹果…...

LRTimelapse 6 for Mac(延时摄影视频制作软件)
LRTimelapse 是一款适用于macOS 系统的延时摄影视频制作软件,可以帮助用户创建高质量的延时摄影视频。该软件提供了直观的界面和丰富的功能,支持多种时间轴摄影工具和文件格式,并具有高度的可定制性和扩展性。 LRTimelapse 的主要特点如下&am…...
:栈与队列)
数据结构和算法(4):栈与队列
栈 ADT 及实现 栈(stack)是存放数据对象的一种特殊容器,其中的数据元素按线性的逻辑次序排列,故也可定义首、末元素。 尽管栈结构也支持对象的插入和删除操作,但其操作的范围仅限于栈的某一特定端。 也就是说…...
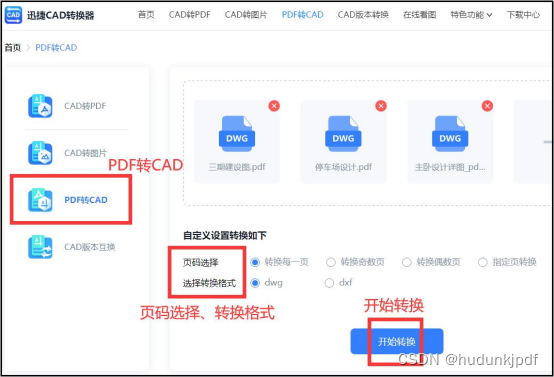
pdf怎么转换成dwg格式?简单转换方法分享
当我们需要在CAD中编辑PDF文件中的向量图形时,将PDF转换成DWG格式是一个非常好的选择。因为PDF是一种非常流行的文档格式,很多时候我们会接收到PDF文件,但是PDF文件中的向量图形无法直接在CAD中编辑。而将PDF转换成DWG格式后,就可…...
uniapp使用H5实现预览pdf文件
下载后把压缩包解压到自己的项目的static文件夹下的pdf文件下,如图 新建一个文件名为filePreview.vue <template><view><web-view :src"allUrl"></web-view></view> </template><script>export default {dat…...

Studio 3T for MongoDB的介绍及语法简单介绍
用法介绍 Studio 3T是一款用于MongoDB数据库管理和开发的图形化工具,它提供了许多功能来简化MongoDB的操作和开发过程。以下是一些常见的Studio 3T用法: 连接到MongoDB服务器: 打开Studio 3T并创建一个新连接配置。输入MongoDB服务器的主机名…...
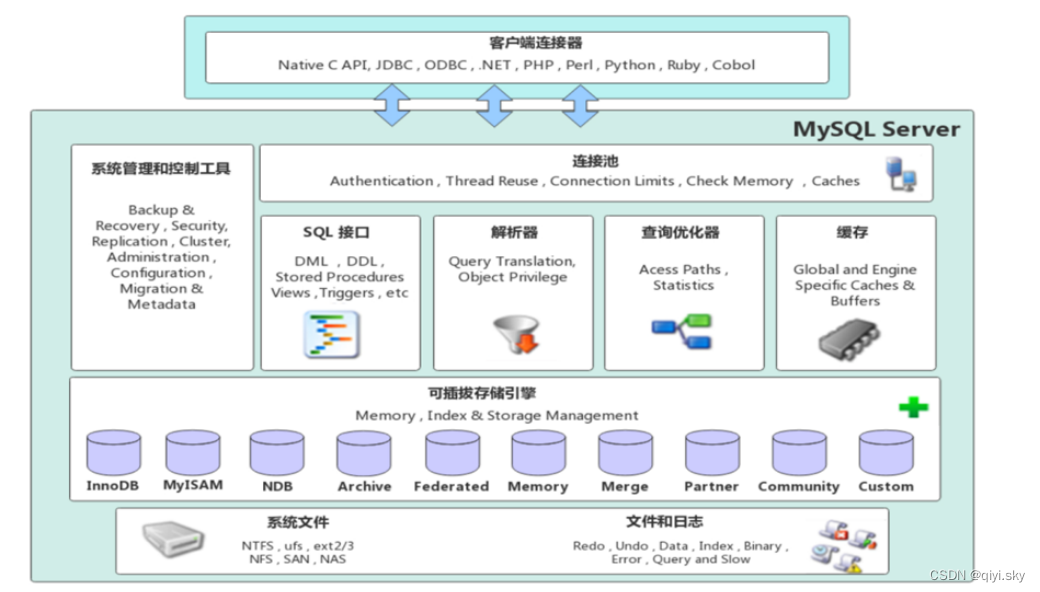
MySQL数据库——存储引擎(1)-MySQL体系结构、存储引擎简介
目录 MySQL体系结构 连接层 服务层 引擎层 存储层 存储引擎简介 概念 语句 演示 下面开始学习进阶篇的第一个内容——存储引擎 分为四点学习: MySQL体系结构存储引擎简介存储引擎特点存储引擎选择 MySQL体系结构 连接层 最上层是一些客户端和链接服务&am…...

211. 添加与搜索单词 - 数据结构设计
211. 添加与搜索单词 - 数据结构设计 class WordDictionary { public:struct Node{Node *node[26];bool is_end;Node(){is_endfalse;for(int i0;i< 26;i){node[i]NULL;}}};Node *root;WordDictionary() {root new Node();}void addWord(string word) {auto p root;for(aut…...
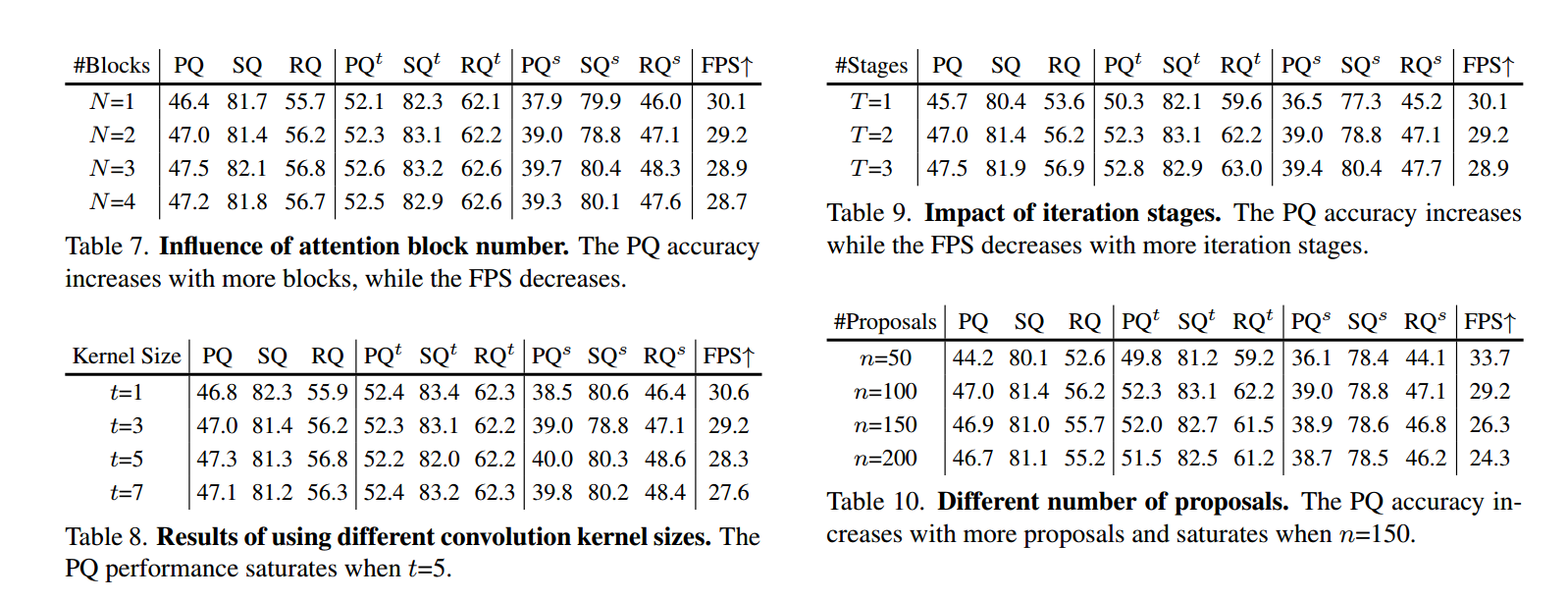
【深度学习】You Only Segment Once: Towards Real-Time Panoptic Segmentation,YOSO全景分割
论文:https://arxiv.org/abs/2303.14651 代码:https://github.com/hujiecpp/YOSO 文章目录 Abstract1. Introduction2. Related Work3. Method3.1. Task Formulation3.2. Feature Pyramid Aggregator3.3. Separable Dynamic Decoder 4. Experiments4.1. …...
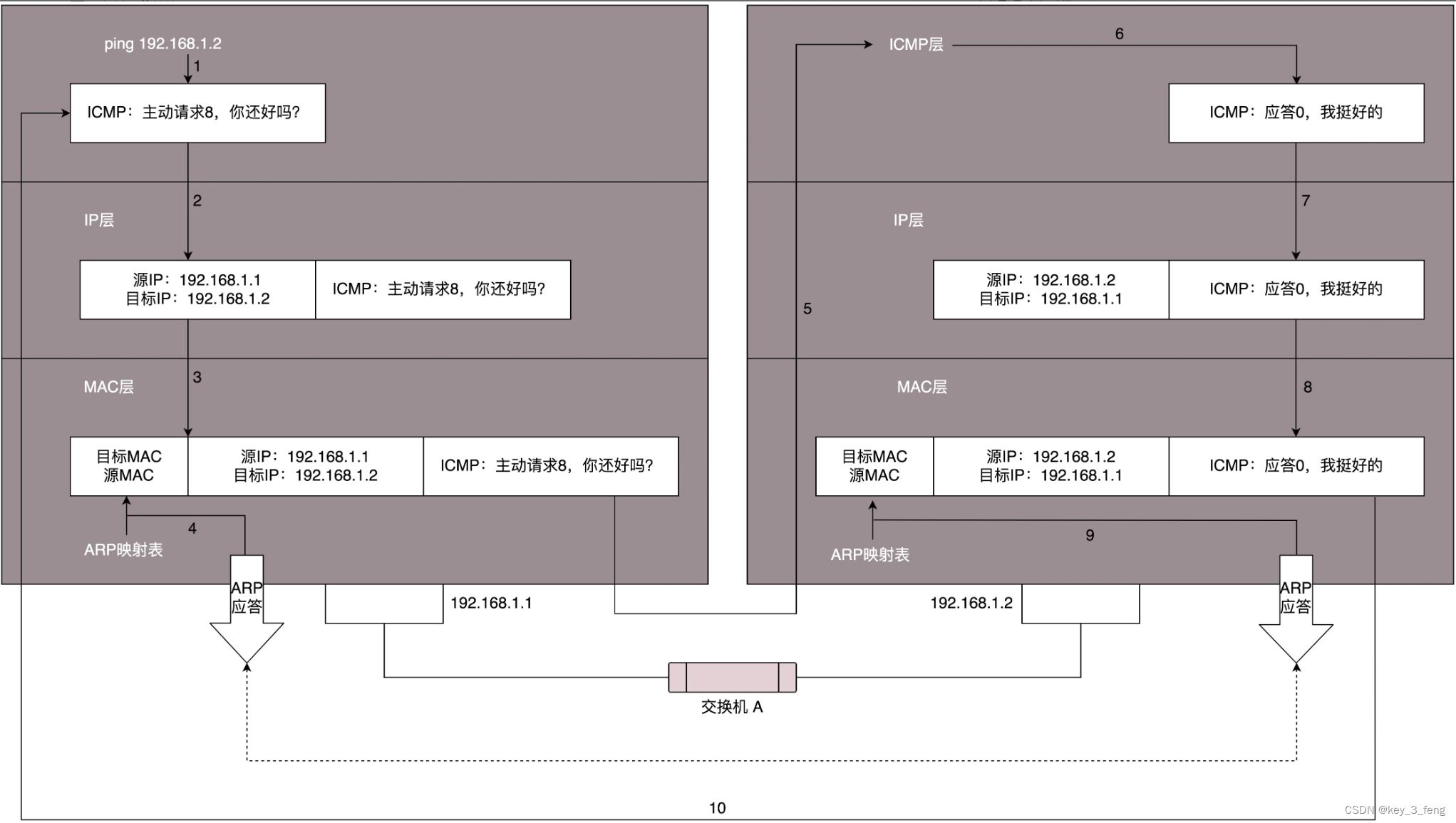
ping与Traceroute是如何工作的
ping 是基于 ICMP 协议工作的。ICMP 全称 Internet Control Message Protocol,就是互联网控制报文协议。 ICMP 报文是封装在 IP 包里面的。因为传输指令的时候,肯定需要源地址和目标地址。它本身非常简单。 ICMP 报文有很多的类型,不同的类型…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...
