初高(重要的是高中)中数学知识点综合
1. 集合
1.1 集合的由来和确定性
确定对象构成的整体称为集合(组成集合的元素必须是确定的 ),每个集合内的对象个体成为元素(Element)。确定性: 给定一个集合,任何一个对象是不是这个集合内的元素,就已经确定了。
比如,我国的四大发明,造纸术,印刷术,火药,指南针。就是一个明确的构成,这个集合就是四大发明。
四大发明 = {造纸术,印刷术,火药,指南针}
每个集合内的元素,使用逗号隔开。
元素和集合之间,存在 属于/不属于 两种关系,拿上面的四大发明集合来讲,比如:
造纸术属于四大发明集合;手机不属于四大发明集合;
火药属于四大发明集合;机关枪不属于四大发明集合;
为了方便书写,采用方便的符号形式来进行代替。
属于: ∈ 不属于: ∉
在用上述的例子,替换为符号就是
造纸术 ∈ 四大发明集合;手机 ∉ 四大发明集合;
火药 ∈ 四大发明集合;机关枪 ∉ 四大发明集合;
如果给定一个集合, {大学计算机系所有的高个子学生},那么这就是一个没有办法确定的内容,不能形成一个集合。你没办法明确知道高个子到底是多高。 如果是 {大学计算机系所有身高 > 170的高个子学生},那么这就给我们划分了一个很明确的界限,大于 170 cm 的同学,都可以被划分为高个子学生列表。那么就能形成一个集合。
测试题
1. 大于 3 小于 11 的偶数。 (是)
2. 我国的小河流。 (不是)
3. 所有的正方形。 (是)
4. 本班跑步很快的同学。 (不是)
5. 与1接近的实数的全体。 (不是)
6. 1——10以内的全体质数。 (是)
总结
1. 集合是一个由确定对象构成的整体。
2. 集合内的对象称为元素(Element)。
3. 属于 ∈ / 不属于 ∉
4. 集合的确定性,给定一个集合,任何一个对象是不是这个集合内的元素,就已经确定了。
5. 可见,对于给定一个集合和给定一个对象,这个对象是否为这个集合的元素,只有 “是” 与 “不是”,这两种情况,这就是集合中元素
所具有的确定性。
1.2 集合中元素的特性

-
确定性
借鉴上面。 -
互异性
在集合中,集合内的元素必须是互异的,也就是说,对于一个给定的集合,他的任何两个元素都是不同的。
因为集合中的元素是没有重复现象的,所以任何两个相同的元素在同一集合内,只能算作这个集合中的一个元素。
- 无序性
集合与其中元素的排列次序无关,也就是说集合中的元素是不排序的。
例如: {1, 2} 也可以写成 {2, 1},他们两个是一样的。
1.3 常见数集
1.3.1 学习目标
- 理解常见数集的定义。
- 熟记常见数集的符号。
- 会判断数字与不同数集之间的关系。
1.3.2 自然数(Natural Number) 用以计量事物的件数 : N
自然数英语为 Natural Number, 所以用 大写 N 来表示自然数集。
N = {1, 2, 3, 4, 5, 6, 7...}
在1993年对于自然数集做了重新定义,定义为:
- 不小于 0 的所有整数叫 自然数集 / 非负整数 的集,也就是说,0 也是自然数集内的元素
扩展,在中国大陆2000年后的数学教材,自然数集内都包括 0。
在N后做一些特殊标记也有不同的意义,比如:
- N* : 除0意外的自然数集
- N+ : (+可以在N上面,也可以在N下面)正自然数集。
- 以此类推…
1.3.2 整数集(Whole Number): Z
整数并没有用 W 来表示整数集,有一种说法是:德国女数学家,诺特 (1882-1935)德意志数学家,抽象代数的奠基人,她提出的整数环对于整数有重大的意义 所以整数取得是德语 Zahlen(支付,数字)的首字母,Z。
Z = {0, 1, -1, 2, -2....}
1.3.3 分数 (两个整数之比 — 商)
分数,指的是两个整数之比,古希腊数学家毕达哥拉斯提出了万物皆数的概念,还发现了著名的黄金比例。他们认为,整数和分数,就可以解释整个世界了。
1.3.4 有理数:两个整数之比 — 商(Quotient) : Q
所以,有理数采用商的首字母,Q来表示有理数集。准确来说。有理数包括整数和分数
- Q = {整数和非零整数的比}
整数也可以表示成 9/1 (一分之九),8/1,5/1。 分数也可以表示为, 1/2, 3/8, 1/3
1.3.5 无理数:根号二是有理数吗?
并不是,常见的无理数有,开不尽的根号。 根号3,根号5,根号7,根号9.1 …, 无限不循环小数 Π = 3.1415926535…,自然数e等。不过到目前为止,无理数还没有统一的字幕表示。所有的有理数 + 无理数就是实数。
1.3.6 实数(Real Number):R
实数集是所有的有理数 + 无理数,实数集是目前所学的最大的数集。我们所有学习过的数字都在这个集合里面。
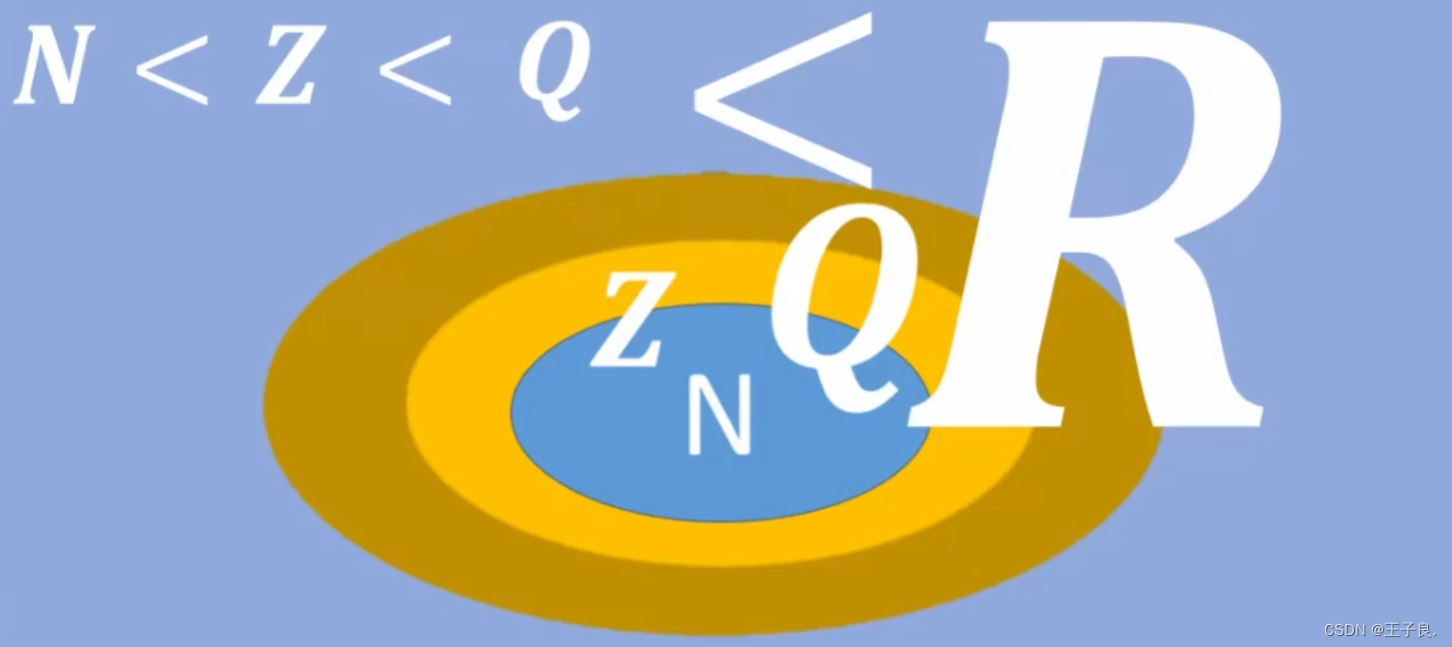
1.3.7 练习题
用符号 “∈” 或者 “∉”填空。
1. 5__N, -5__N, 0__N2. 3__Z, -3__Z, 3.1__Z3. 3.14__Q, Π__Q, 根号2__Q4. Π__R, 3.1__R, 根号三__R
答案
N是自然数集,大于切等于0的整数都是数集内的内容1. ∈,∉,∈Z是整数集,大于小于等于0的所有整数都属于集合内的内容。2. ∈,∈,∉Q是有理数集,也就是两数之比和所有的整数(小数,分数,正整数,负整数,0)3. ∈,∉,∉R是实数集,包括了N,Z,Q,无理数集,是学习过的最大的数集4. ∈,∈,∈
特殊符号集
1. 0__N+, 0__Z+, 0__R*
2. -3__Z+, -3__Z-, -3__Z*
答案
在数集后面跟 + 表示数集内的所有正数对象, - 表示所有的复数对象,R表示0除外的所有对象
3. ∉,∉,∉
4. ∉,∈,∈
1.3.8 总结
学习了各个数集。总结内容如下
- N(自然数集) < Z(整数集) < Q(有理数集) < R(实数集),实际上是不能这样表示的,需要稍微改造一下。
- N(自然数集) ∈ Z(整数集) ∈ Q(有理数集) ∈ R(实数集)
1.4 集合的表示方法
相关文章:
初高(重要的是高中)中数学知识点综合
1. 集合 1.1 集合的由来和确定性 确定对象构成的整体称为集合(组成集合的元素必须是确定的 ),每个集合内的对象个体成为元素(Element)。确定性: 给定一个集合,任何一个对象是不是这个集合内的元素,就已经确…...
Fiddler 系列教程(二) Composer创建和发送HTTP Request跟手机抓包
Fiddler Composer介绍 Composer的官方帮助文档:http://www.fiddler2.com/fiddler/help/composer.asp Fiddler的作者把HTTP Request发射器取名叫Composer(中文意思是:乐曲的创造者), 很有诗意 Fiddler Composer的功能就是用来创建HTTP Request 然后发送…...

淘宝平台开放接口API接口
淘宝平台开放接口API接口是指淘宝平台提供给第三方开发者的一组接口,用于实现与淘宝平台的数据交互和功能扩展。通过API接口,第三方开发者可以获取淘宝平台上的商品信息、订单信息、用户信息等数据,也可以实现商品的发布、订单的创建和支付等…...

缓存夺命连环问
1. 为什么要用缓存? 用缓存,主要有两个用途:高性能、高并发。 高性能 假设这么个场景,你有个操作,一个请求过来,吭哧吭哧你各种乱七八糟操作 MySQL,半天查出来一个结果,耗时 600m…...

模型生成自动化测试用例
自动产生的测试用例本就应该由程序自动执行,这其实也就是NModel推荐的模式。先回过头来看看文章中制作的模型,模型里面将登录、注销、用户名以及密码等要素都抽象出来了,而NModel是以这些抽象出来的动作(登录、注销)和…...

归并排序-面试例子
小数和问题 描述 在一个数组中,一个数左边比它小的数的总和,叫数的小和,所有数的小和累加起来,叫数组小和。求数组小和。 例子 5 2 6 1 7 小和原始的求法是:任何一个数左边比它小的数累加起来。 5左边比它小数累加…...
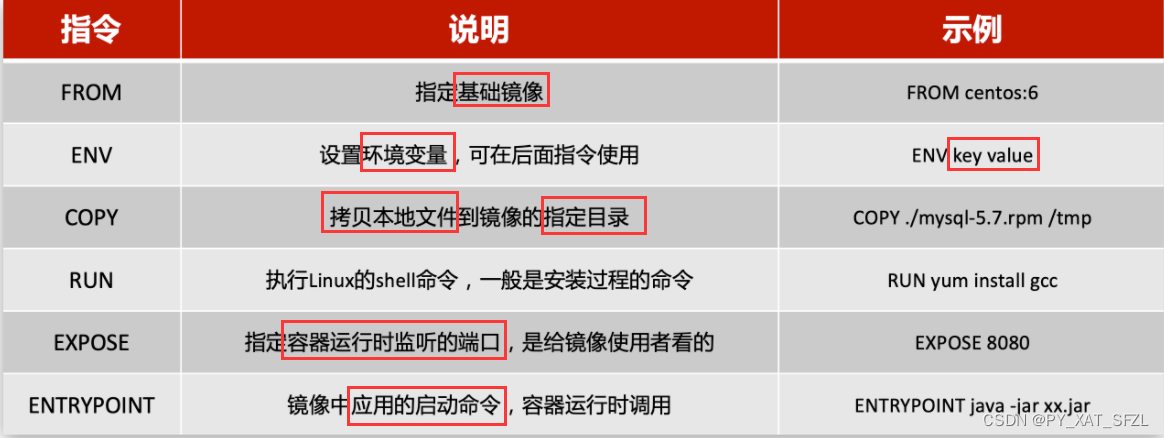
docker 生成镜像的几个问题
docker 生成镜像的几个问题 根据jdk8.tar.gz 打包Jdk8 镜像失败运行镜像报错差不多是网络ip错误,在网上说重启docker即可解决运行mysql5.7.25 镜像失败向daemon.json文件添加内容导致docker重启失败docker run 命令常用参数根据jdk8.tar.gz 打包Jdk8 镜像失败 首选做准备工作…...

云计算时代的采集利器
大家好!在今天的知识分享中,我们将探讨一个在云计算环境中的爬虫应用利器——独享IP。如果你是一名爬虫程序员,或者对数据采集和网络爬虫有浓厚的兴趣,那么这篇文章将向你展示独享IP在云计算环境下的应用价值。 1. 什么是独享IP&…...

【Unity编辑器扩展】| Inspector监视器面板扩展
前言【Unity编辑器扩展】| Inspector监视器面板扩展一、ContextMenu和ContextMenuItem二、Custom Editors 自定义编辑器三、Property Drawer 属性绘制器总结前言 前面我们介绍了Unity中编辑器扩展的一些基本概念及基础知识,还有编辑器扩展中用到的相关特性Attribute介绍。后面…...

Redis配置
关系型数据库和非关系型数据库 ①了解关系和非关系 关系型数据库 一个结构化的数据库,创建在关系模型基础上,一般面向于记录,包括Oracle、MySQL、SQL Server、Microsoft Access、DB2、postgreSQL等 非关系型数据库 除了主流的关系型数据库…...

CSDN每日一练 |『小艺照镜子』『Ctrl+X,Ctrl+V』『括号上色』2023-09-11
CSDN每日一练 |『小艺照镜子』『Ctrl+X,Ctrl+V』『括号上色』2023-09-11 一、题目名称:小艺照镜子二、题目名称:Ctrl+X,Ctrl+V三、题目名称:括号上色一、题目名称:小艺照镜子 时间限制:1000ms内存限制:256M 题目描述: 已知字符串str。 输出字符串str中最长回文串的长度…...

React 全栈体系(四)
第二章 React面向组件编程 六、组件的生命周期 1. 效果 需求:定义组件实现以下功能: 让指定的文本做显示 / 隐藏的渐变动画从完全可见,到彻底消失,耗时2S点击“不活了”按钮从界面中卸载组件 <!DOCTYPE html> <html lang"e…...

各种UI库使用总结
各种UI库使用总结 工作了这么年,使用了一些UI库,简单的总结一下,UI库也是五花八门,根据自己的产品,应用场景吧,没有绝对合适的,各有各的应用场景吧! QT 这几年前后在一些嵌入式上…...
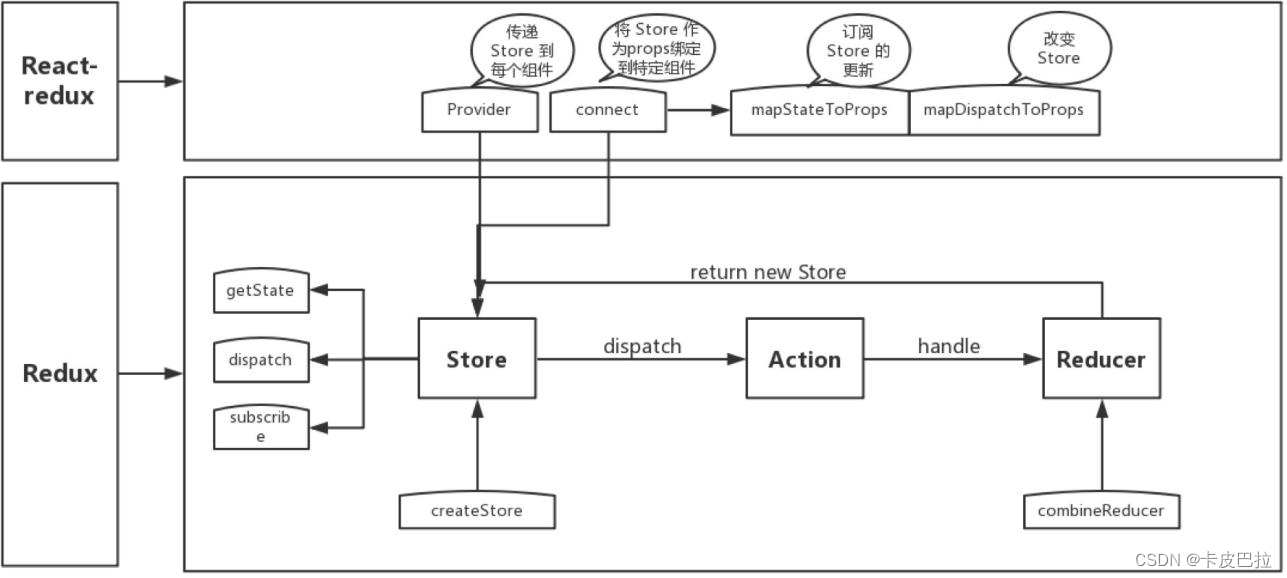
2023Web前端开发面试手册
HTML基础 1. HTML 文件中的 DOCTYPE 是什么作用? HTML超文本标记语言: 是一个标记语言, 就有对应的语法标准 DOCTYPE 即 Document Type,网页文件的文档类型标准。 主要作用是告诉浏览器的解析器要使用哪种 HTML规范 或 XHTML规范…...
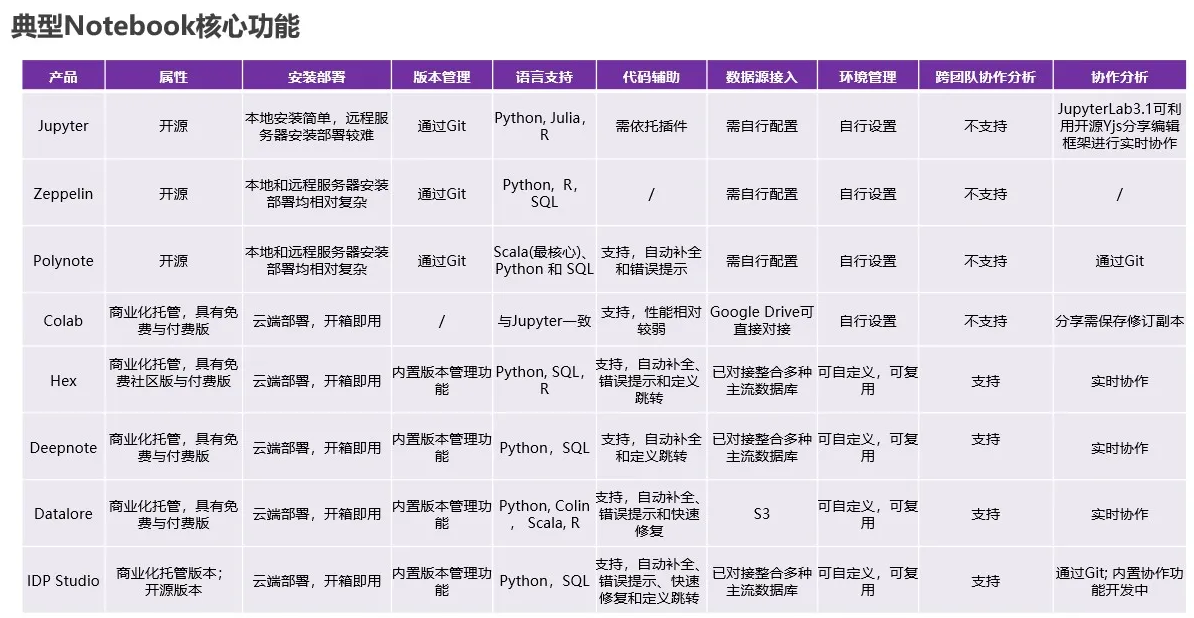
一文了解数据科学Notebook
编者按: 主要介绍什么是Notebook,Notebook在数据科学领域的应用的重要性与优势,以及数据科学家/算法团队在选择Notebook时需考虑哪些关键因素。同时,基于Notebook的筛选考量维度,对常见的Notebook进初步对比分析&#…...

2020年12月 C/C++(二级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:数组指定部分逆序重放 将一个数组中的前k项按逆序重新存放。例如,将数组8,6,5,4,1前3项逆序重放得到5,6,8,4,1。 时间限制:1000 内存限制:65536 输入 输入为两行: 第一行两个整数,以空格分隔,分别为数组元素的个数n(1 < n…...

关于ChatGPT的个人的一些观点
问题 1 Q: 你认为ChatGPT是一款非常有用的工具吗? A: 我认为ChatGPT是一款非常有用的工具。它可以帮助人们解决各种问题,包括技术问题、心理问题、生活问题等等。同时,ChatGPT也可以成为人们分享想法和交流的平台,增强人与人之间…...
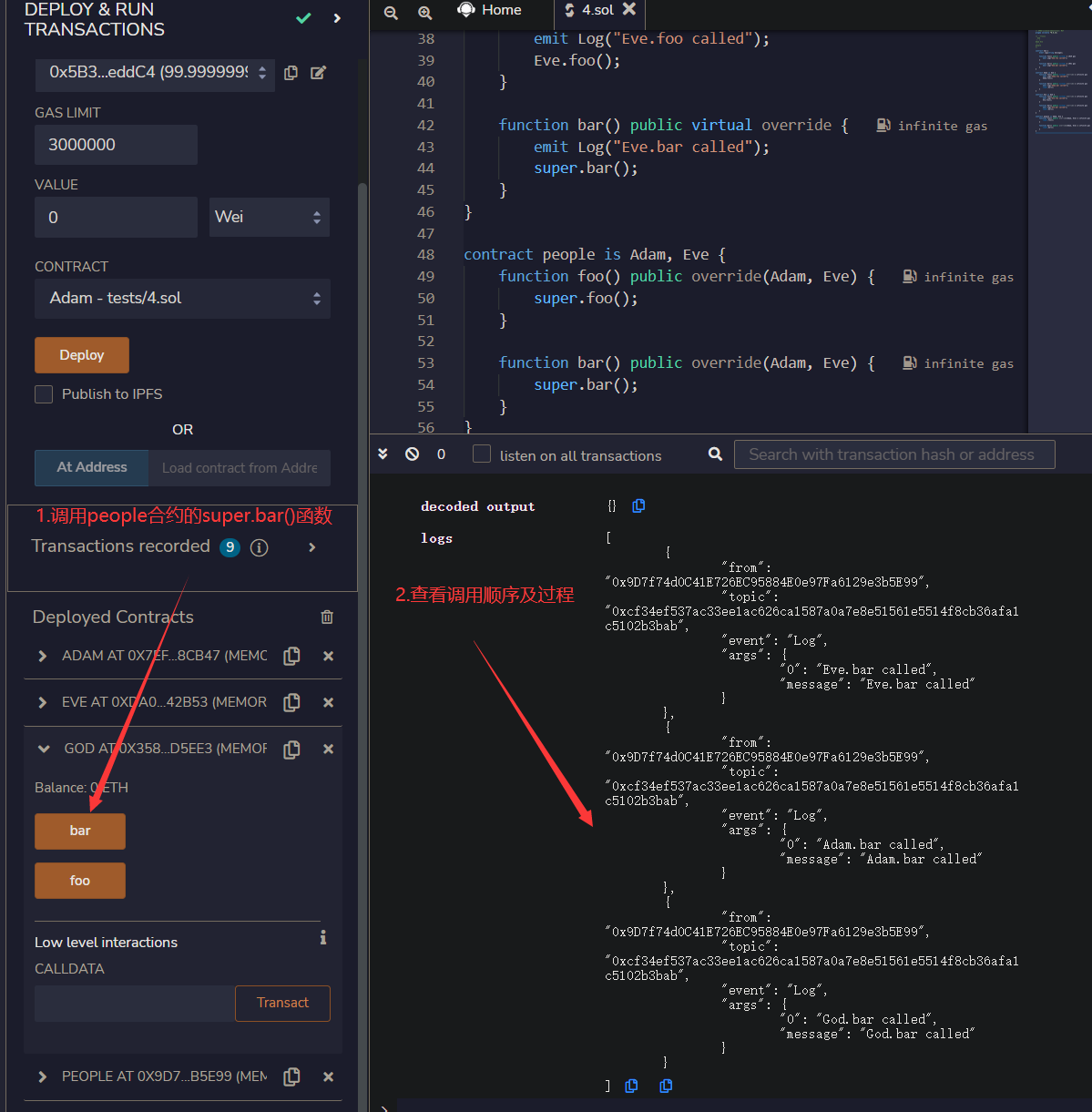
Solidity 小白教程:13. 继承
Solidity 小白教程:13. 继承 这一讲,我们介绍solidity中的继承(inheritance),包括简单继承,多重继承,以及修饰器(modifier)和构造函数(constructorÿ…...

队列(Queue)的顶级理解
目录 1.队列(Queue) 的概念 2.单链表模拟实现队列 2.1创建队列 2.2入队列 2.3判断是否为空 2.4出队列 2.5获取队头元素 2.6完整代码: 2.7双向链表模拟实现队列代码 3.数组模拟实现队列代码 3.1创建队列 3.2判断是否为满 3.3检查是否为空 3.4插入元素 3…...

选择 Guava EventBus 还是 Spring Framework ApplicationEvent
文章首发地址 Spring Framework ApplicationEvent Spring Framework 的 ApplicationEvent 是 Spring 框架提供的一种事件机制,用于实现发布和订阅事件的功能。它基于观察者模式,允许应用程序内的组件之间进行松耦合的通信。 下面是关于 Spring Frame…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

逻辑回归暴力训练预测金融欺诈
简述 「使用逻辑回归暴力预测金融欺诈,并不断增加特征维度持续测试」的做法,体现了一种逐步建模与迭代验证的实验思路,在金融欺诈检测中非常有价值,本文作为一篇回顾性记录了早年间公司给某行做反欺诈预测用到的技术和思路。百度…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

CSS3相关知识点
CSS3相关知识点 CSS3私有前缀私有前缀私有前缀存在的意义常见浏览器的私有前缀 CSS3基本语法CSS3 新增长度单位CSS3 新增颜色设置方式CSS3 新增选择器CSS3 新增盒模型相关属性box-sizing 怪异盒模型resize调整盒子大小box-shadow 盒子阴影opacity 不透明度 CSS3 新增背景属性ba…...

Springboot多数据源配置实践
Springboot多数据源配置实践 基本配置文件数据库配置Mapper包Model包Service包中业务代码Mapper XML文件在某些复杂的业务场景中,我们可能需要使用多个数据库来存储和管理不同类型的数据,而不是仅仅依赖于单一数据库。本技术文档将详细介绍如何在 Spring Boot 项目中进行多数…...
【Docker 02】Docker 安装
🌈 一、各版本的平台支持情况 ⭐ 1. Server 版本 Server 版本的 Docker 就只有个命令行,没有界面。 Platformx86_64 / amd64arm64 / aarch64arm(32 - bit)s390xCentOs√√Debian√√√Fedora√√Raspbian√RHEL√SLES√Ubuntu√√√√Binaries√√√ …...
