基于AHP模型指标权重分析python整理
一 背景介绍
- 日常会有很多定量分析的场景,然而也会有一些定性分析的场景
- 针对定性分析的场景,预测者只能通过主观判断分析能力来推断事物的性质和发展趋势
- 然而针对个人的直觉和虽然能够有一定的协助判断效果,但是很难量化到指标做后期的复用 AHP层次分析法可以将定性分析和定量分析更好地融合
二 AHP简单介绍
AHP(Analytic Hierarchy Process,简称AHP)中文名称为层次分析法,是美国运筹学匹兹堡大学教授萨蒂于20世纪70年代提出,用于将决策相关的因素划分不同层次,做定性和定量分析结合的方法。
其主要的思路为将决策分层三个层次:
- 最高层:最终决策的目的、要解决的问题,即目标层
- 中间层:主因素,考虑的因素、决策的准则层
- 最低层:决策时的备选方案,也可为中间层的子因素,方案层
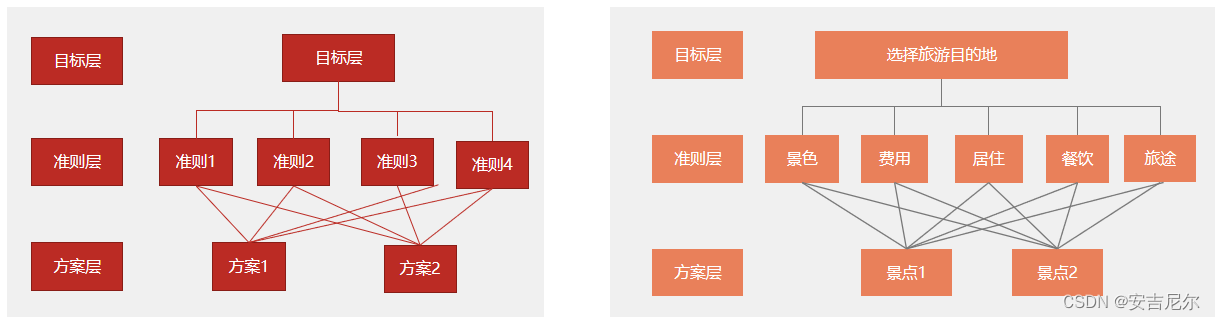
整体决策的思路为:
1.构建层次评价模型:有明确的准则(指标)、可选方案、目标
2.基于AHP确定指标定权重
3.基于指标权重,计算量化后的方案选择
其中指标权重确认的整个步骤为:
1.构建指标判断矩阵(也就是指标两两比较,用数字区分重要程度)
2.进行权重的计算
3.进行一致性校验(保证比较是合理的)
4.进行层次总排序
5.进行方案选择
计算原理详细步骤细节建议可以参考相关书籍内容

三 相关代码
说明:
- 由于做测试数据结果验证,做了特殊的手工入口录入
- 可以根据实际录入需求做导入对象替换,或者原始数据数组粘贴对象替换
调试代码参考
import numpy as np# 计算指标权重的判断矩阵
def calculate_weights(comparison_matrix):num_indicators = comparison_matrix.shape[0]eigenvalues, eigenvectors = np.linalg.eig(comparison_matrix)max_eigenvalue_index = np.argmax(eigenvalues)max_eigenvector = eigenvectors[:, max_eigenvalue_index]weights = max_eigenvector / np.sum(max_eigenvector)return weights# 输入当前指标对应不同方案的打分判断矩阵
def input_comparison_matrix(indicator):num_solutions = len(indicator)comparison_matrix = np.zeros((num_solutions, num_solutions))for i in range(num_solutions):for j in range(i+1, num_solutions):comparison = float(input("{}相对{}的比较重要性为:".format(indicator[i], indicator[j])))comparison_matrix[i][j] = comparisoncomparison_matrix[j][i] = 1 / comparisonreturn comparison_matrix# 进行一致性检验
def consistency_check(comparison_matrix):num_criteria = comparison_matrix.shape[0]# 计算特征向量eigenvalues, eigenvectors = np.linalg.eig(comparison_matrix)max_eigenvalue = max(eigenvalues)max_eigenvector = eigenvectors[:, np.argmax(eigenvalues)].real# 计算一致性指标CIconsistency_index = (max_eigenvalue - num_criteria) / (num_criteria - 1)# 计算随机一致性指标RIrandom_index = {1: 0,2: 0,3: 0.58,4: 0.90,5: 1.12,6: 1.24,7: 1.32,8: 1.41,9: 1.45,10: 1.49,11: 1.51,12: 1.48,13: 1.56,14: 1.57,15: 1.59}random_index_value = random_index.get(num_criteria)# 计算一致性比例CRconsistency_ratio = consistency_index / random_index_valuereturn consistency_ratio#主程序
# 计算指标的权重结果
num_indicators = int(input("请输入指标的数量:"))
indicators = []
for i in range(num_indicators):indicator = input("请输入第{}个指标:".format(i+1))indicators.append(indicator)
# 进行指标权重的比较,并计算指标的权重结果
indicator_comparison_matrix = input_comparison_matrix(indicators)
indicator_weights = calculate_weights(indicator_comparison_matrix)#计算录入不同方案的比较矩阵
num_solutions = int(input("请输入方案的数量:"))
solutions = []
for i in range(num_solutions):solution = input("请输入第{}个方案:".format(i+1))solutions.append(solution)#计算不同方案在同一指标下评估占比的权重
solution_weight_matrix = np.zeros((num_indicators, num_solutions))
solution_check_list = []
for indicator in range(num_indicators):print("请根据{}对不同方案的重要程度进行比较:".format(indicators[indicator]))comparison_matrix = input_comparison_matrix(solutions)solutions_weight = calculate_weights(comparison_matrix)solution_check = consistency_check(comparison_matrix)solution_weight_matrix[indicator] = solutions_weightsolution_check_list.append(solution_check)# 计算不同方案综合比较结果
scores = np.dot(indicator_weights,solution_weight_matrix)# 进行一致性检验
indicator_check = consistency_check(indicator_comparison_matrix)# 输出评估结果
print("指标权重结果为:")
print(indicator_weights)
print("不同指标对应方案的综合打分结果为:")
print(solution_weight_matrix)
print("方案综合评选结果为:")
print(scores)
print("指标检验和方案检验,进行一致性检验结果如下:")
print(indicator_check,solution_check_list)
输出结果参考:
请输入指标的数量:3
请输入第1个指标:指标1
请输入第2个指标:指标2
请输入第3个指标:指标3
指标1相对指标2的比较重要性为:3
指标1相对指标3的比较重要性为:2
指标2相对指标3的比较重要性为:2
请输入方案的数量:2
请输入第1个方案:方案1
请输入第2个方案:方案2
请根据指标1对不同方案的重要程度进行比较:
方案1相对方案2的比较重要性为:2
请根据指标2对不同方案的重要程度进行比较:3
请根据指标3对不同方案的重要程度进行比较:
方案1相对方案2的比较重要性为:3
指标权重结果为:
[0.54721643+0.j 0.26307422+0.j 0.18970934+0.j]
不同指标对应方案的综合打分结果为:
[[0.66666667 0.33333333][0.75 0.25 ][0.75 0.25 ]]
方案综合评选结果为:
[0.70439863+0.j 0.29560137+0.j]
指标检验和方案检验,进行一致性检验结果如下:
(-0.7451630649499623+0j) [-inf, -inf, -inf]相关文章:

基于AHP模型指标权重分析python整理
一 背景介绍 日常会有很多定量分析的场景,然而也会有一些定性分析的场景针对定性分析的场景,预测者只能通过主观判断分析能力来推断事物的性质和发展趋势然而针对个人的直觉和虽然能够有一定的协助判断效果,但是很难量化到指标做后期的复用 …...

用python实现基本数据结构【02/4】
*说明 如果需要用到这些知识却没有掌握,则会让人感到沮丧,也可能导致面试被拒。无论是花几天时间“突击”,还是利用零碎的时间持续学习,在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢?列表、字典、集…...
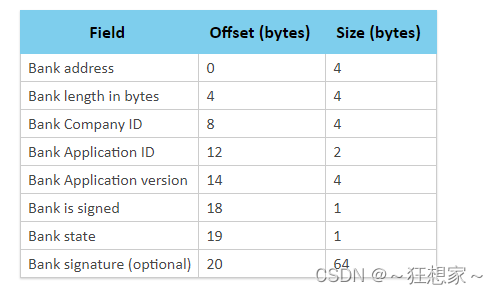
蓝牙Mesh专有DFU
蓝牙Mesh专有DFU Mesh专有DFU协议介绍特征DFU模式和类型角色并发传输混合设备的网络传输速率后台操作传输分区内存映射安全DFU固件IDApplication firmware IDSoftDevice firmware IDBootloader firmware ID 设备页面格式内容 Mesh专有DFU协议介绍 设备固件更新(Device Firmwar…...

浅谈综合管廊智慧运维管理平台应用研究
贾丽丽 安科瑞电气股份有限公司 上海嘉定 201801 摘要:为提升综合管廊运维管理水平,实现管理的数字化转型,采用综合监测系统、BIMGIS 可视化系统、智能机器人巡检、结构安全监测等技术,搭建实时监控、应急管理、数据分析等多功能…...

Httpservletrequest与Httpservletresponse
目录 一、Httpservletrequest 1.1什么是Httpservletrequest 1.2Httpservletrequest中的方法 二、Httpservletresponse 1.1什么是Httpservletresponse 1.2Httpservletresponse的方法 一、Httpservletrequest 1.1什么是Httpservletrequest HttpServletRequest(…...
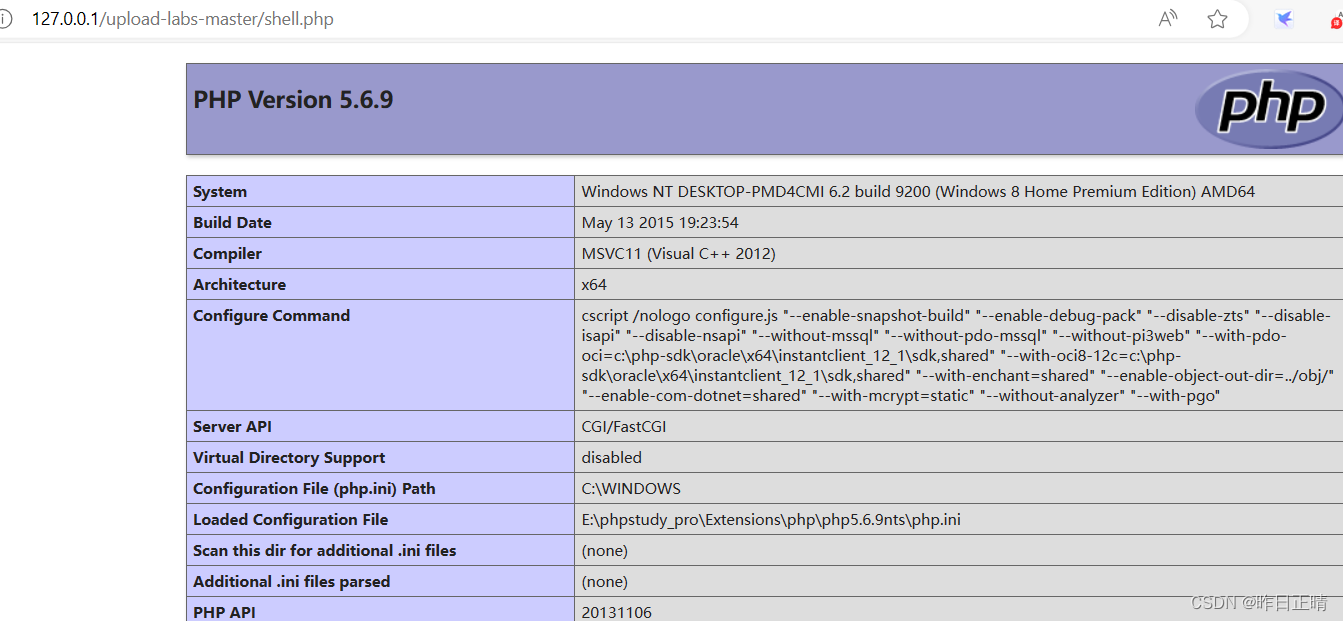
文件上传之图片码混淆绕过(upload的16,17关)
目录 1.upload16关 1.上传gif loadup17关(文件内容检查,图片二次渲染) 1.上传gif(同上面步骤相同) 2.条件竞争 1.upload16关 1.上传gif imagecreatefromxxxx函数把图片内容打散,,但是不会…...
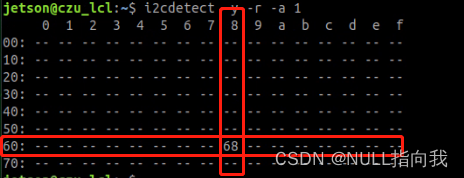
Jetsonnano B01 笔记5:IIC通信
今日继续我的Jetsonnano学习之路,今日学习的是IIC通信,并尝试使用Jetson读取MPU6050陀螺仪数据。文章提供源码。文章主要是搬运的官方PDF说明,这里结合自己实际操作作笔记。 目录 IIC通信: IIC硬件连线: 安装IIC库文…...

【网络爬虫笔记】爬虫Robots协议语法详解
Robots协议是指一个被称为Robots Exclusion Protocol的协议。该协议的主要功能是向网络蜘蛛、机器人等搜索引擎爬虫提供一个标准的访问控制机制,告诉它们哪些页面可以被抓取,哪些页面不可以被抓取。本文将进行爬虫Robots协议语法详解,同时提供…...
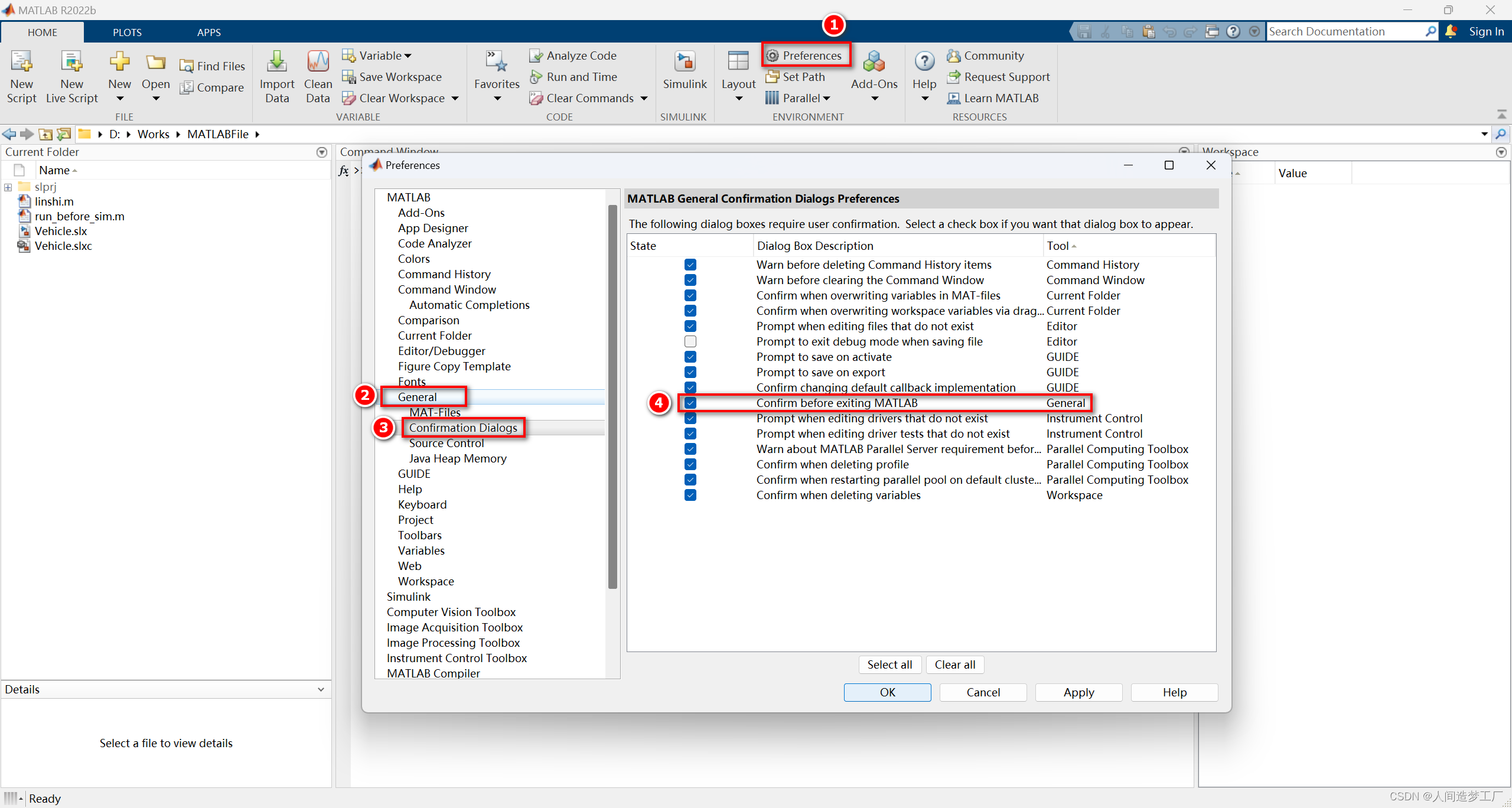
MATLAB 2022b 中设置关闭 MATLAB 之前进行询问
在 MATLAB 2022b 中可以进行设置,在关闭 MATLAB 之前进行询问,防止意外关闭 MATLAB。如图:...

在SpringBoot框架下,接口有读个实现类,在不改变任何源码的情况下,SpringBoot怎么知道给接口注入哪个实现类的依赖呢?
在Spring Boot框架下,当一个接口有多个实现类时,Spring Boot 默认情况下不知道要注入哪个实现类的依赖。因此,你需要使用一些方法来明确告诉Spring Boot应该注入哪个实现类的依赖。 以下是一些常用的方法: 1.使用Qualifier注解&a…...
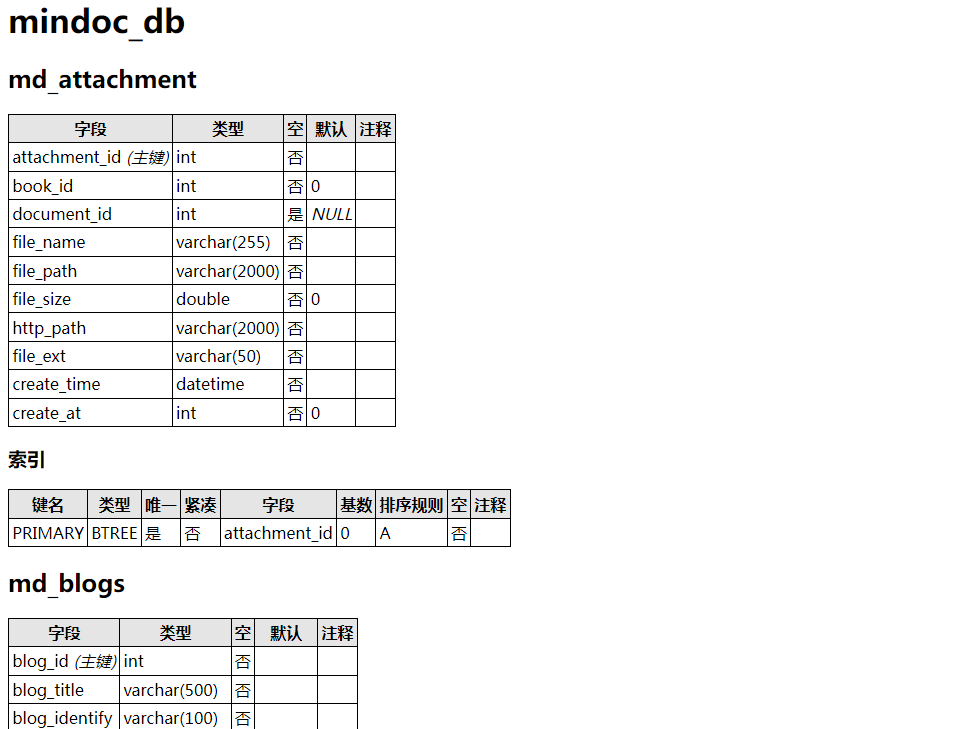
探索数据库管理的利器 - PHPMyAdmin
有一个项目,后端由博主独自负责,最近需要将项目交接给另一位同事。在项目初期,博主直接在数据库中使用工具创建了相关表格,并在完成后利用PhpMyAdmin生成了一份数据字典,供团队使用。然而,在随后的开发过程…...

大数据技术原理与应用学习笔记第1章
黄金组合访问地址:http://dblab.xmu.edu.cn/post/7553/ 1.《大数据技术原理与应用》教材 官网:http://dblab.xmu.edu.cn/post/bigdata/ 2.大数据软件安装和编程实践指南 官网林子雨编著《大数据技术原理与应用》教材配套大数据软件安装和编程实践指…...
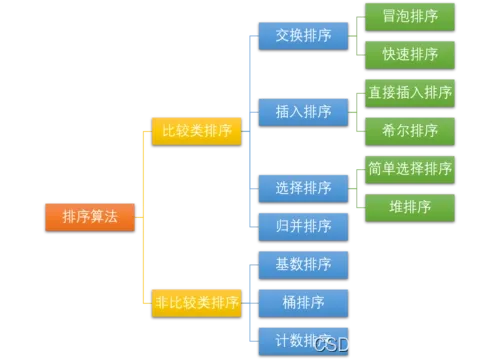
算法从未放弃你,放弃你的只有你自己
在人生的旅程中,我们常常会遇到各种挫折和困难。有些人在面对困境时,会选择放弃,将责任归咎于命运或外部环境。然而,算法教给我们一个重要的道理:永远不要放弃 当我们遇到问题或挑战时,算法可以帮助我们找到…...

[Linux 基础] linux基础指令(1)
文章目录 1、Linux下基本指令1.ls指令2.pwd指令3.cd指令4.touch指令5.mkdir指令6.rmdir指令 && rm指令7.man指令8.cp指令9.mv指令10.cat指令11.more指令12.less指令 Linux学习笔记从今天开始不断更新了。第一篇我们从基础指令开始学起。 1、Linux下基本指令 好多人都说…...

ESP32蓝牙主从站模式:主站发送,从站接收,同时附加简单通信协议
主站发送:WXAiBj,六个字符 蓝牙模式是一个字符一个字符发送 主站和从站设置通信协议 使得六个字符一句话完整接收,同时打印出接收完成信息 硬件电路连接如下: 主从站为两个ESP32,只使用了其中的蓝牙功能 代码如下: 主站: //主机模式 #include <Arduino.h> …...

Redis布隆过滤亿级大数据
场景描述 小程序用户的openid作为最主要的业务查询字段,在做了缓存设计之后仍有非常高频的查询,通过埋点简单统计约在每日1000w次。 其中:由于有新增用户原因,导致请求的openid根本不存在MySQL数据库中,这部分统计约占…...
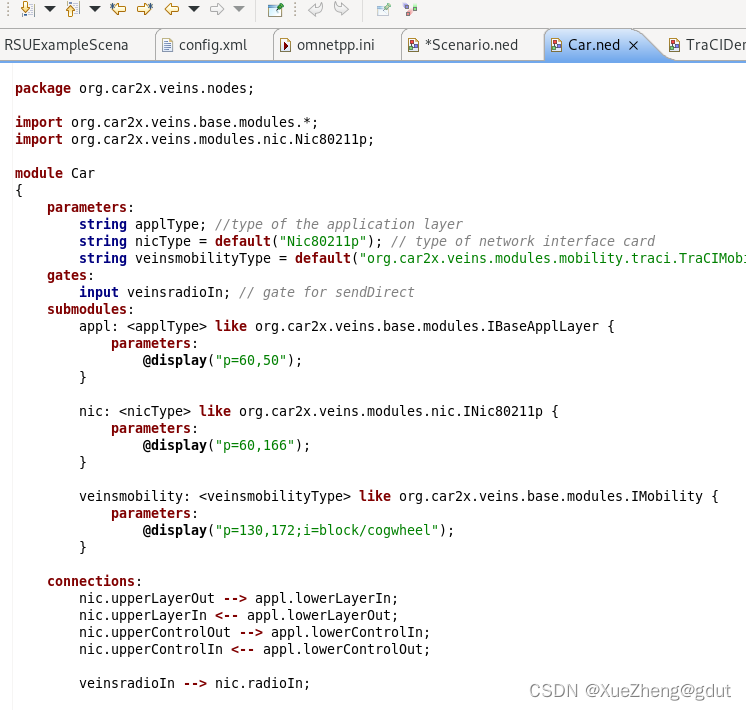
车联网仿真工具Veins学习1
准备条件 假如你是一个小白,先找到相关的参考资料(已根据上一篇博客安装好Veins),主要是官方文档和相关的博客,官方提供了一个example,我找到的资料如下: Frequently Asked Questions (FAQ) O…...

封闭岛屿数量 -- 二维矩阵的dfs算法
1254. 统计封闭岛屿的数目 这道题和 岛屿数量 – 二维矩阵的dfs算法 类似,区别在于不算边缘部分的岛屿,那其实很简单,把上⼀题中那些靠边的岛屿排除掉,剩下的就是「封闭岛屿」了。 关于岛屿的相似题目: 岛屿数量 –…...

C语言_指针(1)
文章目录 前言一、指针数组1.1利用指针数组模拟出二维数组 二、数组指针2.1数组名是数组首元素的地址2.2 二维数组传参2.3 一级指针传参2.4 二级指针传参 三. 函数指针四 . typedef 重命名 前言 指针数组是由指针组成的数组。它的每个元素都是一个指针,可以指向任何…...
--- 网站基本常识)
建站系列(一)--- 网站基本常识
目录 相关系列文章前言一、因特网二、网站三、服务器四、IP五、域名六、DNS七、Hosts文件八、端口号九、URL十、静态网站十一、动态网站 相关系列文章 建站系列(一)— 网站基本常识 建站系列(二)— 域名、IP地址、URL、端口详解 …...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...
