当前位置：首页 > news >正文

第六章图六、最小生成树（Prim算法、Kruskal算法）

news 文章来源：https://blog.csdn.net/icbbm/article/details/132818355 2024/11/3 4:31:05

一、定义

对于一个带权连通无向图G=(V,E)，生成树不同，每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树(Minimum-Spanning-Tree, MST)。

二、手动实现算法

（1）Prim算法

介绍：从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。

时间复杂度:O( $\left | V \right |^2$ )，适合用于边稠密图

例子1：

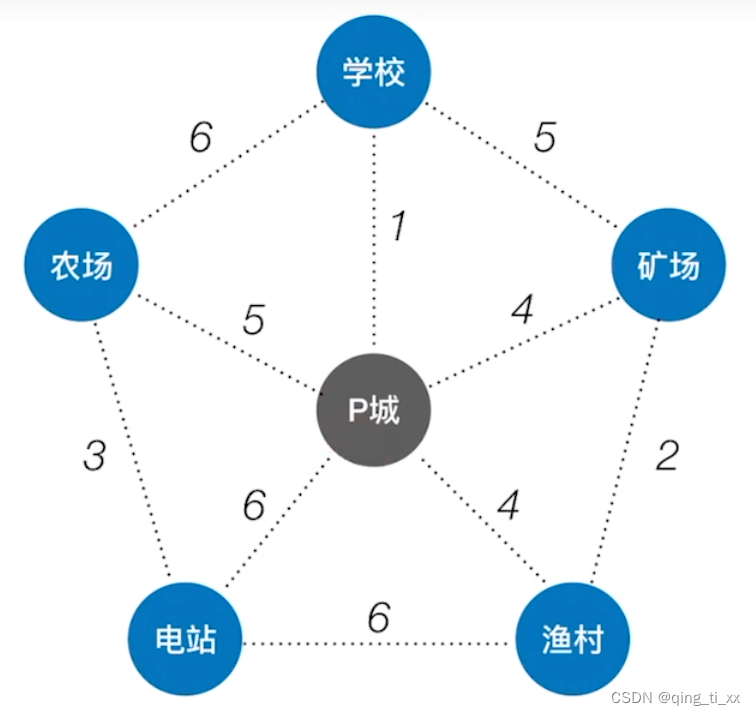
1、我们从P城开始，找到权最小的路径，并构建出新的树。此时最小为1

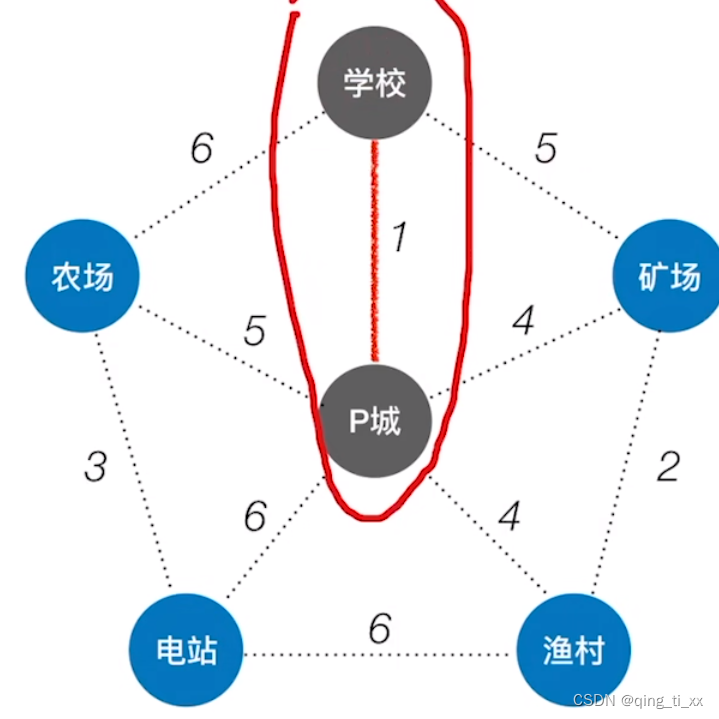
2、再次寻找权最短的路径，为P城到矿场。

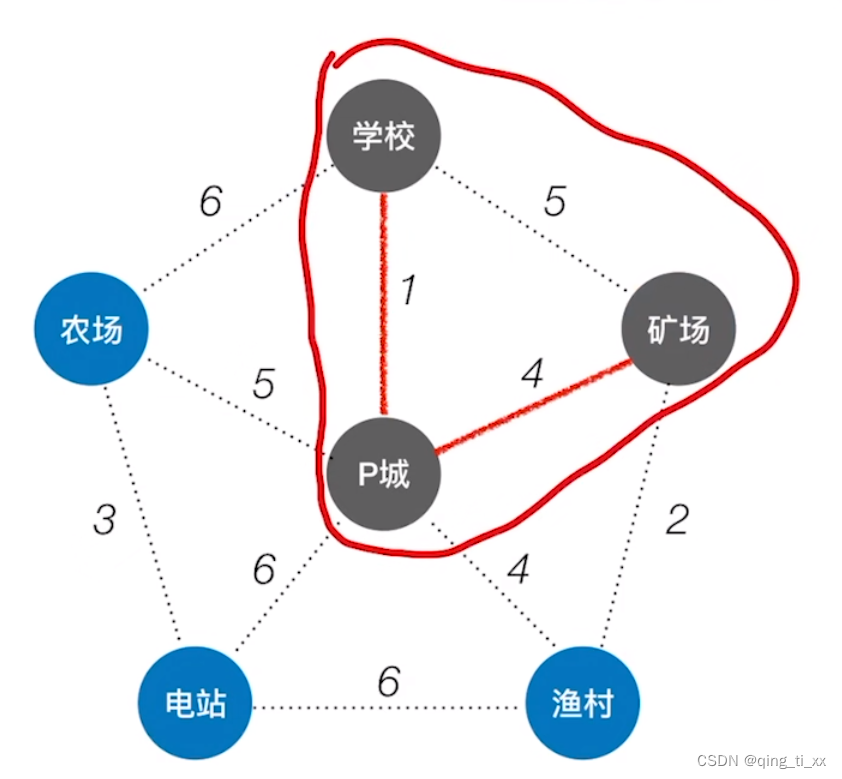
3、如此反复，得到最终结果。

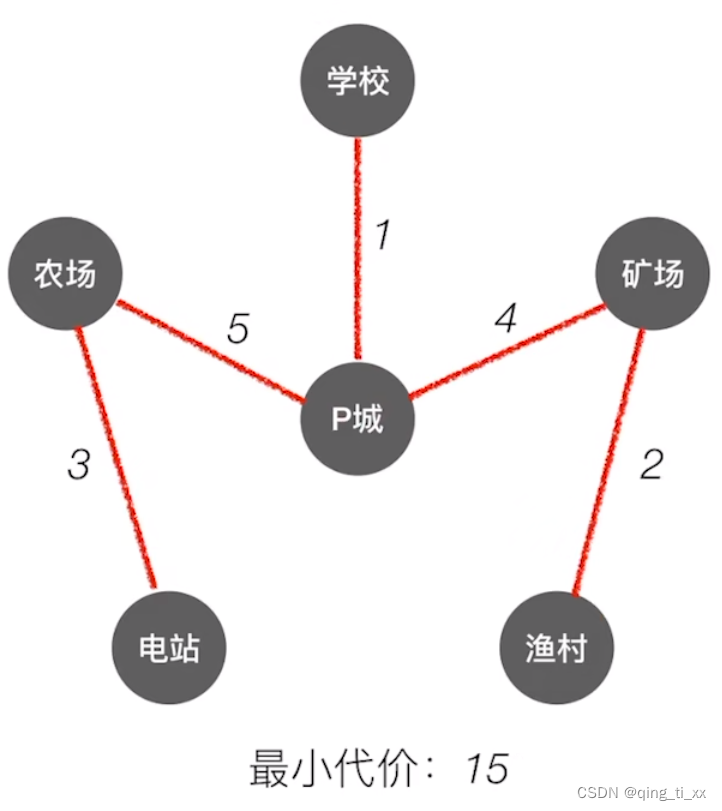
（2）Kruskal算法

介绍：每次选择一条权值最小的边，使这条边的两头连通(原本已经连通的就不选)，直到所有结点都连通。

时间复杂度:O(|E|*log2|E|)，适合用于边稀疏图

例子2：

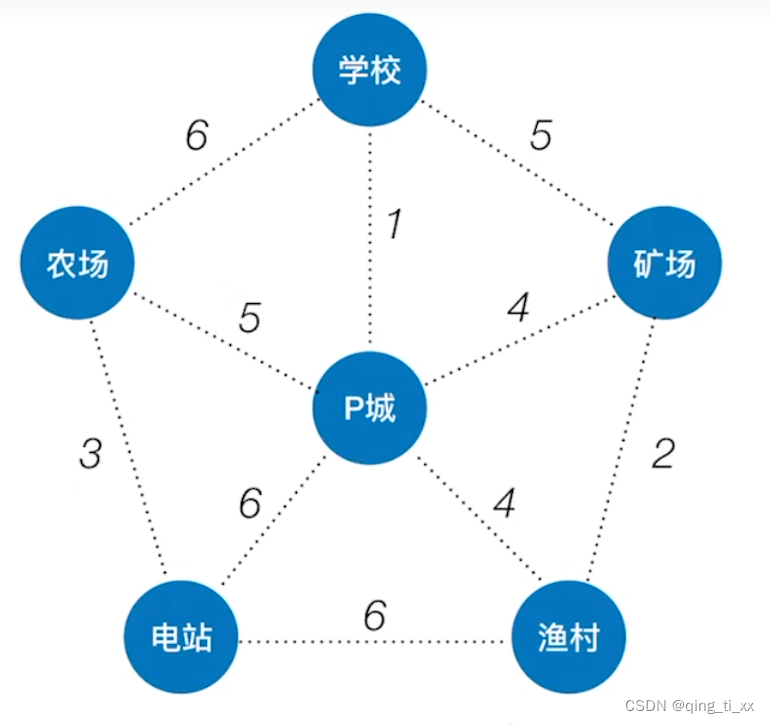
1、我们从P城出发，找一条权值最小的边，我们找到学校到P城的路径为1（最短），于是连通它们。

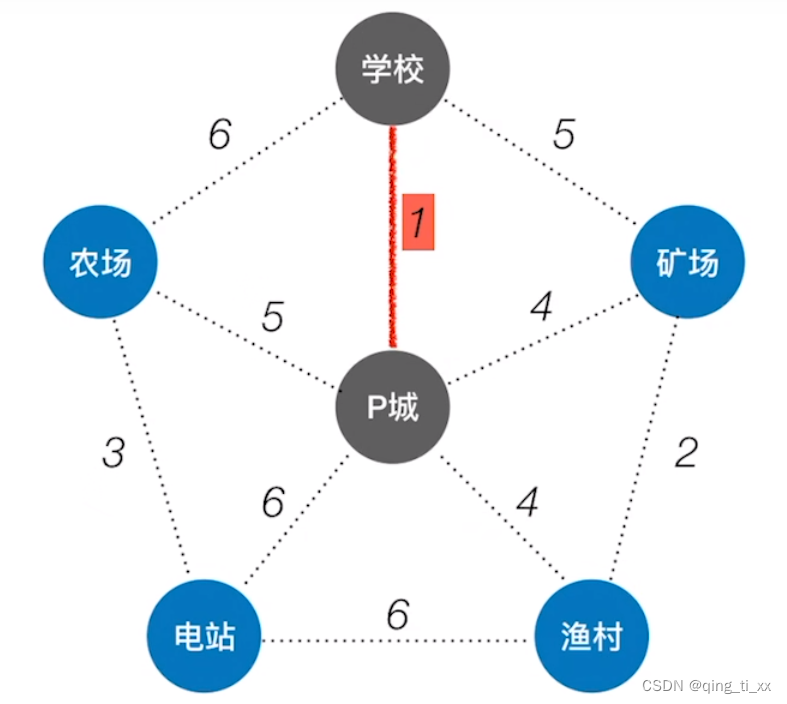
2、再次找最短，找到2，连通它们。

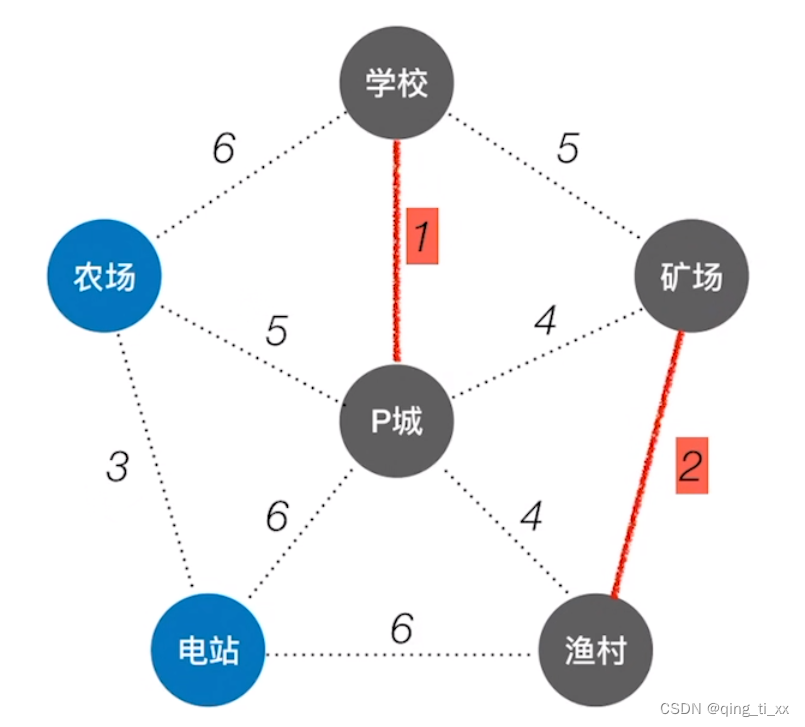
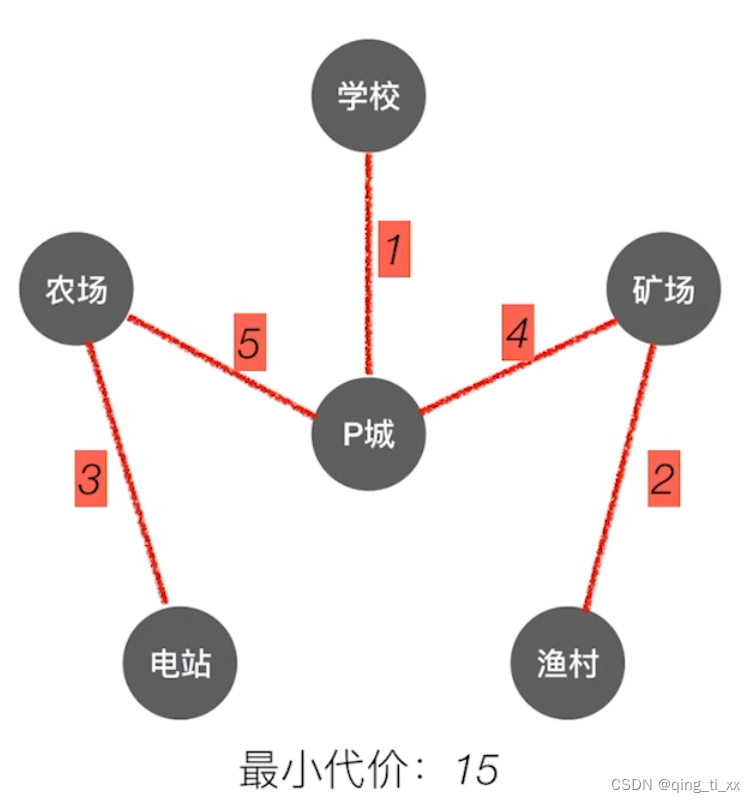
3、反复执行这个操作，直到所有的结点都连通。

第六章图六、最小生成树（Prim算法、Kruskal算法）

一、定义对于一个带权连通无向图G(V,E)，生成树不同，每棵树的权(即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树(Minimum-Spanning-Tree, MST)。二、手…...

编程日记 2023/9/12 0:41:05

机器学习笔记 - 什么是 MLOps？

什么是 MLOps？ Machine learning operations (MLOps) 作为一个新兴领域，MLOps 在数据科学家、机器学习工程师和人工智能爱好者中迅速崛起。MLOps 代表机器学习操作。MLOps 是机器学习工程的核心功能，专注于简化将机器学习模型投入生产、然后维护和监控的过程。MLOps 是一种…...

编程日记 2023/9/12 0:38:31

初阶扫雷（超详解）

✨博客主页：小钱编程成长记 🎈博客专栏：C语言小游戏 🎈推荐相关博文：初阶三子棋（超详解） 初阶扫雷 1.游戏介绍2.基本思路3.实现前的准备4.实现步骤4.1 打印菜单4.2 初始化扫雷棋盘4.3 打印扫雷棋…...

编程日记 2023/9/12 0:37:20

计算机视觉CV：1000字总结介绍

目录 1.CV计算机视觉 2.计算机视觉的应用 3.计算机视觉的基本技术 4.计算机视觉的发展趋势 1.CV计算机视觉计算机视觉（Computer Vision, CV）是指通过计算机技术模拟人类视觉，让计算机能够“看”懂和理解图像和视频。计算机视觉发展了多…...

编程日记 2023/9/12 0:36:14

JavaScript 之 Symbol 数据类型

一、简介 symbol类型是ES6新引入的一种基本数据类型，该类型具有静态属性和静态方法。其中静态属性暴露了几个内建的成员对象，静态方法暴露了全局的symbol注册。 symbol类型具有以下特点：① 唯一性：每个symbol值都是唯一的…...

编程日记 2023/9/12 0:34:57

1.下载Docker 2.设置DockerHub账号 3.运行Docker并下载Image 4.启动PostgreSQL Image 5.连接到数据库运行SQL docker run --name some-postgres -p 5432:5432 -e POSTGRES_PASSWORDmysecretpassword -d postgres 开放端口从Docker容器到主操作系统，这将允许我们…...

编程日记 2023/9/12 0:33:44

实现Spring Boot集成MyBatis

引言在Java开发中，Spring Boot和MyBatis是非常常用的框架。Spring Boot是一个快速开发应用程序的框架，而MyBatis是一个持久化框架，可以方便地操作数据库。本文将介绍如何使用Idea集成Spring Boot和MyBatis，并创建一个简单的示例…...

编程日记 2023/9/12 0:32:44

关于算法的时间复杂度（度量算法执行时间的两种方法、渐进时间复杂度、时间复杂度的几个性质、渐进估算、常见的渐进时间复杂度排序）

目录度量算法执行时间的两种方法事后统计法（Post Hoc Analysis）： 事前统计法（Pre Hoc Analysis）： 渐进时间复杂度时间复杂度的几个性质渐进估算常见的渐进时间复杂度排序度量算法执行时间的两…...

编程日记 2023/9/12 0:31:43

SpringBoot项目--电脑商城【显示商品详情功能】

1.持久层[Mapper] 1规划需要执行的SQL语句根据商品id显示商品详情的SQL语句 SELECT * FROM t_product WHERE id?2 设计接口和抽象方法在ProductMapper接口中添加抽象方法 /*** 根据商品id查询商品详情* param id 商品id* return 匹配的商品详情，如果没有匹配…...

编程日记 2023/9/12 0:30:42

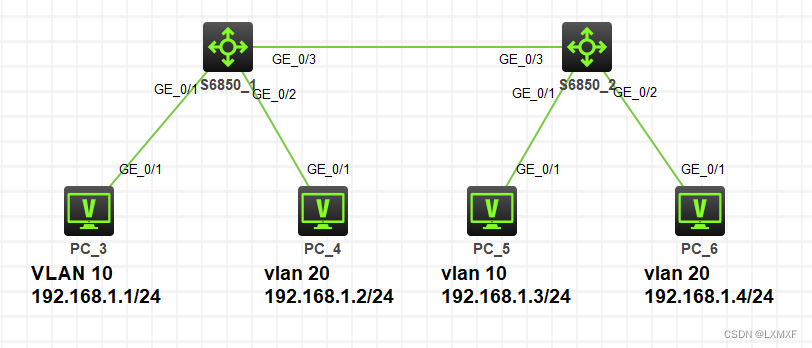
VLAN笔记

虚拟VLAN 什么是VLAN VLAN的作用 VLAN的优缺点 VLAN的配置方法 VLAN有哪些接口模式 access与trunk接口的区别 Hybrid接口拓扑实验enspCiscoH3C 什么是VLAN VLAN（Virtual Local Area Network）又称虚拟局域网，是指在交换局域网的基础上&a…...

编程日记 2023/9/12 0:29:41

分类算法系列⑤：决策树

目录 1、认识决策树 2、决策树的概念 3、决策树分类原理基本原理数学公式 4、信息熵的作用 5、决策树的划分依据之一：信息增益 5.1、定义与公式 5.2、⭐手动计算案例 5.3、log值逼近 6、决策树的三种算法实现 7、API 8、⭐两个代码案例 8.1、决策树…...

编程日记 2023/9/12 0:28:35

前端面试（基础）

一、CSS 1.说一下CSS的盒模型。在HTML页面中的所有元素都可以看成是一个盒子盒子的组成：内容content、内边距padding、边框border、外边距margin 盒模型的类型： 标准盒模型 margin border padding content IE盒模型 margin content(border…...

编程日记 2023/9/12 0:27:33

element-ui switch开关组件二次封装，添加loading效果，点击时调用接口后改变状态

先看效果： element-ui中的switch开关无loading属性（在element-plus时加入了），而且点击时开关状态就会切换，这使得在需要调用接口后再改变开关状态变得比较麻烦。思路：switch开关外包一层div，给…...

编程日记 2023/9/12 0:26:31

【GAN小白入门】Semi-Supervised GAN 理论与实战

🍨 本文为🔗365天深度学习训练营中的学习记录博客🍖 原作者：K同学啊🚀 文章来源：K同学的学习圈子论文原文：Semi-Supervised Learning with Generative Adversarial Networks.pdf在学习GAN的时候你有没有想过这样一个问题呢，如果我们生成的图像是带有标签的，例如数…...

编程日记 2023/9/12 0:25:30

Python自动化测试（1）-自动化测试及基本技术手段概述

生产力概述在如今以google为首的互联网时代，软件的开发和生产模式都已经发生了变化， 在《参与感》一书提到：某位从微软出来的工程师很困惑，微软在google还有facebook这些公司发展的时候，为何为感觉没法有效还击&…...

编程日记 2023/9/12 0:24:29

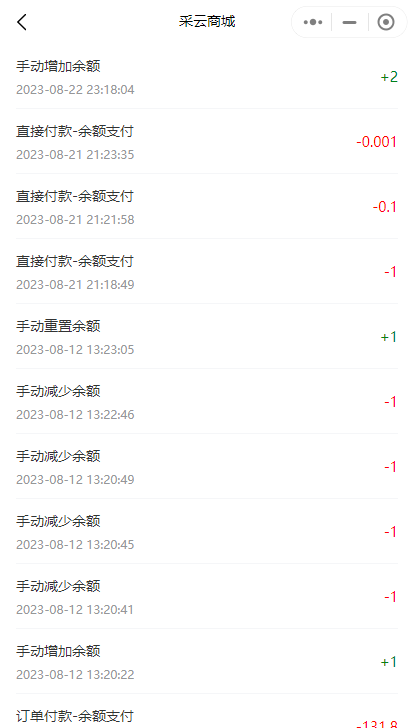
小程序中如何查看会员的余额和变更记录

通过查看会员的余额和变更记录，可以帮助商家更好地管理会员资金，提供更好的服务和用户体验。下面将介绍小程序中如何查看会员的余额以及余额的变更记录。 1. 找到指定的会员卡。在管理员后台->会员管理处，找到需要查看余额和记录的会员…...

编程日记 2023/9/12 0:23:28

【项目经验】elementui--table表格自定义表头及bug

一.思路首先我们肯定得循环表头，我们原生js封装的表格的实现原理就是这样。其次我们要把自己循环的label显示出来，对应的prop也要和表格数据相对应。用div标签循环都会出现错误（div里面套column），大家不要踩坑。第一…...

编程日记 2023/9/12 0:22:27

flink实现kafka、doris精准一次说明

前言说明：本文档只讨论数据源为kafka的情况实现kafka和doris的精准一次写入 flink的kafka连接器已经实现了自动提交偏移量到kafka，当flink中的数据写入成功后，flink会将这批次数据的offset提交到kafka，程序重启时，kafka中记录了当前groupId消费的offset位置，开始消费时将…...

编程日记 2023/9/12 0:21:26

【git】git commit、push之前自动执行脚本

可以使用 Git 的钩子（hooks）功能。Git 钩子是在特定事件发生时执行自定义脚本的方式。下面是一个使用 pre-commit 钩子的例子，用于在执行 git commit 之前自动执行脚本： 进入你的 Git 仓库的根目录。进入 .git/hooks 目录&…...

编程日记 2023/9/12 0:20:24

基于springboot+vue的加盟店管理系统(前后端分离)

博主主页：猫头鹰源码博主简介：Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战主要内容：毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询文末联系获取项目介绍…...

编程日记 2023/9/12 0:19:22

Gin中的Cookie和Session的用法

Gin中的Cookie和Session的用法文章目录 Gin中的Cookie和Session的用法介绍Cookie代码演示 Session代码展示介绍 cookie 和 session 是 Web 开发中常用的两种技术，主要用于跟踪用户的状态信息。 Cookie func (c *Context) Cookie(name string, value string, max…...

编程日记 2023/9/12 0:18:21

【算法】反悔贪心

文章目录反悔贪心力扣题目列表630. 课程表 III871. 最低加油次数LCP 30. 魔塔游戏2813. 子序列最大优雅度洛谷题目列表P2949 [USACO09OPEN] Work Scheduling GP1209 [USACO1.3] 修理牛棚 Barn RepairP2123 皇后游戏（🚹省选/NOI− TODO） 相关…...

编程日记 2023/9/12 0:17:20

Hadoop的安装和使用，Windows使用shell命令简单操作HDFS

1，Hadoop简介 Hadoop是一个能够对大量数据进行分布式处理的软件框架，并且是以一种可靠、高效、可伸缩的方式进行处理的，它具有以下几个方面的特性。高可靠性。高效性。高可扩展性。高容错性。成本低。运行在Linux平台上。支持多种编程…...

编程日记 2023/9/12 0:16:18

ubuntu上ffmpeg使用framebuffer显示video

这个主题是想验证使用fbdev(Linux framebuffer device），将video直接显示到Linux framebuffer上，在FFmpeg中对应的FFOutputFormat 就是ff_fbdev_muxer。 const FFOutputFormat ff_fbdev_muxer {.p.name "fbdev",.p.long_…...

编程日记 2023/9/12 0:15:17

82 # koa-bodyparser 中间件的使用以及实现

准备工作安装依赖 npm init -y npm i koakoa 文档：https://koajs.cn/# koa 中不能用回调的方式来实现，因为 async 函数执行的时候不会等待回调完成 app.use(async (ctx, next) > {console.log(ctx.path, ctx.method);if (ctx.path "/login…...

编程日记 2023/9/12 0:14:16

计算一串输出数字的累加和

计算一个文件内数字的累加和 awk {sum$1}END{print sum} 直接抽取数据以后的打印是这样的 cat step-iostat.1125.log |grep sda |cut -c "49-56" |awk {sum$1}END{print sum}...

编程日记 2023/9/12 0:13:15

python包导入原理解析

原文链接： https://www.cnblogs.com/hi3254014978/p/15317976.html 根据编程经验的不同，我们在运行程序时可能经常或者偶尔碰到下面这些问题，仔细观察后会发现这些问题无一例外都出现了一个相同的短语，很容易就可以发现&#xff0…...

编程日记 2023/9/12 0:12:11

MNIST手写数字辨识-cnn网路 (机器学习中的hello world，加油)

用PyTorch实现MNIST手写数字识别(非常详细) - 知乎 (zhihu.com) 参考来源（这篇文章非常适合入门来看，每个细节都讲解得很到位） 一、模块函数用法-查漏补缺： 1.关于torch.nn.functional.max_pool2d()的用法： 上述示例…...

编程日记 2023/9/12 0:11:10

论文笔记《3D Gaussian Splatting for Real-Time Radiance Field Rendering》

项目地址原论文 Abstract 最近辐射场方法彻底改变了多图/视频场景捕获的新视角合成。然而取得高视觉质量仍需神经网络花费大量时间训练和渲染，同时最近较快的方法都无可避免地以质量为代价。对于无边界的完整场景（而不是孤立的对象）和 10…...

编程日记 2023/9/12 0:10:09

数据库管理系统，数据库，sql的基本介绍以及它们之间的关系

数据库管理系统（Database Management System，简称DBMS）是一种软件工具或系统，用于管理和维护数据库的创建、访问、更新和管理。DBMS允许用户在数据库中存储、检索和操作数据，同时提供了数据安全性、完整性和一致性的控…...

编程日记 2023/9/12 0:09:08

店面设计费一般多少钱一平/宁波网站优化公司哪家好

1、登录mysql服务器 mysql -uroot -p 2、查询mysql服务器安装位置 # 以下两个sql任意一个可查询 select basedir as basePath from dual ; show variables like %basedir%; 参考：https://www.cnblogs.com/phpper/p/10773004.html 转载于:https://www.cnblogs.com/zq…...

编程日记 2024/11/3 4:25:58

郑州百度seo网站优化/如何做谷歌seo推广

获取服务器信息$sysos $_SERVER["SERVER_SOFTWARE"]; //获取服务器标识的字串$sysversion PHP_VERSION; //获取PHP服务器版本//以下两条代码连接mysql数据库并获取MySQL数据库版本信息mysql_connect("localhost", "mysql_user", "mysql_p…...

编程日记 2024/11/3 3:09:29

wordpress 多站点合集/推广网站的方法有哪些

模板介绍精美PPT模板设计，深红色组织结构图表合集PPT模板。一套可视图表幻灯片模板，内含红色多种配色，精美风格设计，动态播放效果，精美实用。一份设计精美的PPT模板，可以让你在汇报演讲时脱颖而出。希…...

编程日记 2024/11/2 23:26:11

做网站有什么用出/全媒体广告投放平台

第一步：建立数据库(这部分已经在《关于oracle中自增字段问题总结》一文中写过。点此查看第二步：创建一个查询过程，因为在登录时要根据用户名查询用户密码此步要用到pl/sql编程知识，代码如下：create or replace procedu…...

编程日记 2024/11/2 21:52:35

徐州品牌网站建设/今日新闻国内大事件

word条形码换行Tables can be difficult to read. Adding shaded bands to a table improves readability and really just makes it look better. Here’s how you can add striping to your Excel tables. 表格可能很难阅读。在表中添加阴影带可提高可读性，实际…...

编程日记 2024/11/2 20:37:41

做网站融资/今天最新的新闻

一．概述 suite套件，就是多个测试的集合，可以同时测试多个测试类。二．TestSuite的两种用法在写用法之前，先做点准备工作。 demo.php <?phpclass Demo{public function add($a, $b){return $a $b; } }业务类&a…...

编程日记 2024/11/2 16:47:02