时间复杂度与空间复杂度详解
时间复杂度与空间复杂度详解🦖
- 一、算法效率
- 1.1 如何衡量一个算法的好坏
- 1.2 算法的复杂度
- 二、时间复杂度
- 2.1 时间复杂度的定义
- 2.2 大O的渐进表示法
- 2.3 如何记录表示算法复杂度
- 三、空间复杂度
- 3.1 空间复杂度的定义
- 3.2 小试牛刀
一、算法效率
1.1 如何衡量一个算法的好坏
-
我一直有个问题,算法到底如何比较,如何衡量一个算法的好坏?
-
我的理解:
-
思路巧妙,神来之笔!
枯燥的代码,却带着无限的智慧,也是这智慧让程序员在学习过程中一次次惊呼:妙哉!此法妙哉!!所以对我而言,一个奇巧的思路是竞赛衡量的一个标准(主观感受)
-
时间、空间资源利用!
一串好的算法代码不一定是简洁的,但一定是空间、时间资源占用少的。
1.2 算法的复杂度
- 算法在编写成可执行程序运行时,需要耗费时间资源和空间资源,因此衡量一个算法的好坏,是从时间和空间两个维度上衡量的,即时间复杂度和空间复杂度。
- 时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间大小。
二、时间复杂度
2.1 时间复杂度的定义
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
举个例子:
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
Func1 执行的基本操作次数 :
- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
根据上述带入尝试,我们不难得出Func1执行的基本操作次数是下面这个函数表达式:
F ( N ) = N 2 + 2 ∗ N + 10 (数学表达式) F(N) = N^2 + 2*N + 10(数学表达式) F(N)=N2+2∗N+10(数学表达式)
在实际计算中,我们并不会计算精准的次数,一般采取估算量级,所以我们会使用大O的渐进表示法
2.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项(高数极限思想)。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:
O ( N 2 + 2 ∗ N + 10 ) − − > O ( N 2 ) O(N^2 + 2*N + 10)-->O(N^2) O(N2+2∗N+10)−−>O(N2)
总结一下: 大O渐进表示法主要是记录复杂度量级,去掉了那些对结果影响不大的项。
2.3 如何记录表示算法复杂度
一个算法运行过程往往有三种衡量记录情况:
最坏情况: 任意输入规模的最大运行次数(上界)
平均情况: 任意输入规模的期望运行次数
最好情况: 任意输入规模的最小运行次数(下界)
所以可以描述一个算法的复杂度范围,来表示算法的复杂度范围,但实际中我们往往采用最坏的情况来表示记录一个算法的复杂度(我也喜欢,因为每一次运行都只会有惊喜!!!)
三、空间复杂度
3.1 空间复杂度的定义
-
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度(额外空间大小) 。
-
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
3.2 小试牛刀
实例1:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i-1] > a[i]){Swap(&a[i-1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
实例1:我们必须明确的是:空间复杂度记录的是额外的临时变量空间大小,因此我们再看实例1的时候,只会计算end、exchange、i等临时变量大小即可。不用计算数组a开辟的空间大小。所以这里空间复杂度就是O(1);
实例2:
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{if(n==0)return NULL;long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));fibArray[0] = 0;fibArray[1] = 1;for (int i = 2; i <= n ; ++i){fibArray[i] = fibArray[i - 1] + fibArray [i - 2];}return fibArray;
}
实例2:这里相当于malloc,创建了n+1个临时空间大小,因此也非常简单,这里空间复杂度也就是O(N)。
这就是最基本的。空间复杂度相较于时间复杂度要简单很多,通常不是O(N)就是O(1)。
相关文章:

时间复杂度与空间复杂度详解
时间复杂度与空间复杂度详解🦖 一、算法效率1.1 如何衡量一个算法的好坏1.2 算法的复杂度 二、时间复杂度2.1 时间复杂度的定义2.2 大O的渐进表示法2.3 如何记录表示算法复杂度 三、空间复杂度3.1 空间复杂度的定义3.2 小试牛刀 一、算法效率 1.1 如何衡量一个算法…...

目录操作函数
mkdir函数 rmdir函数 删除空目录 rename函数 换名 chdir函数 修改当前的工作目录 getcwd函数 获取当前工作的路径...
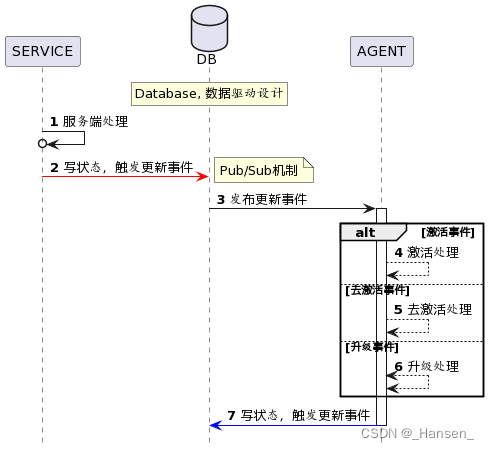
PlantUML入门教程:画时序图
软件工程中会用到各种UML图,例如用例图、时序图等。那我们能不能像写代码一样去画图呢? 今天推荐一款软件工程师的作图利器--PlantUML,它能让你用写代码的方式快速画出UML图。 一、什么是PlantUML? PlantUML是一个允许你快速作出…...

C#范围运算符
C#8.0语法中,范围运算符是一种用于快速截取序列的运算符,其语法为 “start…end”,表示从序列的 “start” 索引处开始,一直截取到"end" 索引处为止(包括 “end” 索引处的元素)。范围运算符主要…...
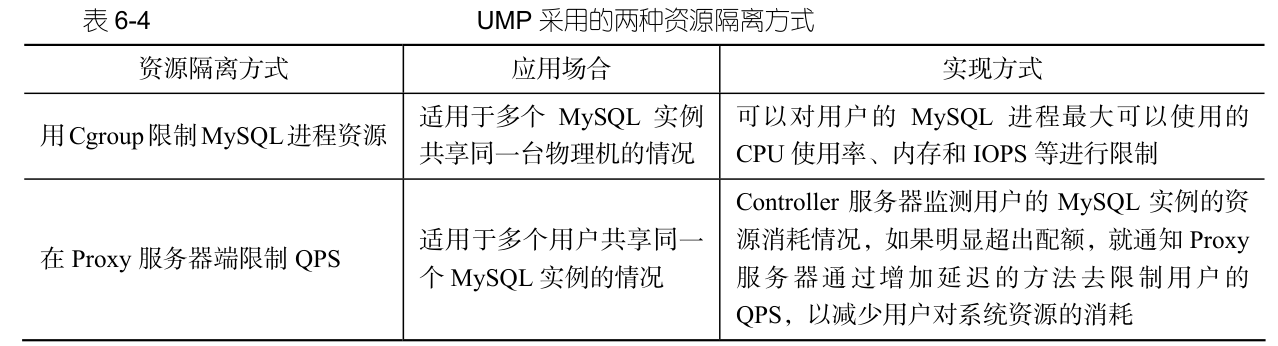
云数据库知识学习——云数据库产品、云数据库系统架构
一、云数据库产品 1.1、云数据库厂商概述 云数据库供应商主要分为三类。 ① 传统的数据库厂商,如 Teradata、Oracle、IBM DB2 和 Microsoft SQL Server 等。 ② 涉足数据库市场的云供应商,如 Amazon、Google、Yahoo!、阿里、百度、腾讯…...

C++中引用详解!
前言: 本文旨在讲解C中引用的相关操作,以及引用的一些注意事项!搬好小板凳,干货来了! 引用的概念 何谓引用呢?引用其实很容易理解,比如李华这个同学,他因为很调皮,所以…...

VUE3+TS项目无法找到模块“../version/version.js”的声明文件
问题描述 在导入 ../version/version.js 文件时,提示无法找到模块 解决方法 将version.js改为version.ts可以正常导入 注意,因为version.js是我自己写的模块,我可以直接该没有关系,但是如果是引入的其他的第三方包,…...

数据结构-堆的实现及应用(堆排序和TOP-K问题)
数据结构-堆的实现及应用[堆排序和TOP-K问题] 一.堆的基本知识点1.知识点 二.堆的实现1.堆的结构2.向上调整算法与堆的插入2.向下调整算法与堆的删除 三.整体代码四.利用回调函数避免对向上和向下调整算法的修改1.向上调整算法的修改2.向下调整算法的修改3.插入元素和删除元素函…...

Spring 条件注解没生效?咋回事
条件注解相信各位小伙伴都用过,Spring 中的多环境配置 profile 底层就是通过条件注解来实现的,松哥在之前的 Spring 视频中也有和大家详细介绍过条件注解的使用,感兴趣的小伙伴戳这里:Spring源码应该怎么学?。 从 Spr…...

96. 不同的二叉搜索树
class Solution { public:int numTrees(int n) {if (n0) {return 1;}vector<int> dp(n1, 0);dp[0] 1;dp[1] 0;for (int i 1; i < n; i) {for (int j 0; j < i; j) {dp[i] dp[j] * dp[i - 1 - j];}}return dp[n];} };...

Android Jetpack 中Hilt的使用
Hilt 是 Android 的依赖项注入库,可减少在项目中执行手动依赖项注入的样板代码。执行 手动依赖项注入 要求您手动构造每个类及其依赖项,并借助容器重复使用和管理依赖项。 Hilt 通过为项目中的每个 Android 类提供容器并自动管理其生命周期,…...

批量采集的时间管理与优化
在进行大规模数据采集时,如何合理安排和管理爬取任务的时间成为了每个专业程序员需要面对的挑战。本文将分享一些关于批量采集中时间管理和优化方面的实用技巧,帮助你提升爬虫工作效率。 1. 制定明确目标并设置合适频率 首先要明确自己所需获取数据的范…...

uniApp监听左右滑动事件
监听左右滑动事件的步骤 1. 添加需要监听滑动事件的元素 在你的页面中,添加需要监听滑动事件的元素。这可以是一个 view、swiper 或其他组件,取决于你的需求。例如: <template><view class"body" touchstart"touc…...
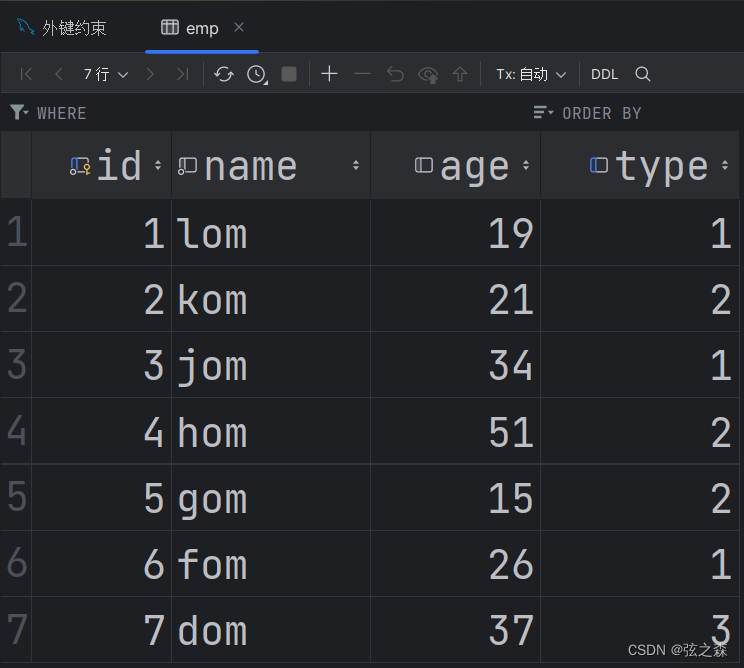
十八、MySQL添加外键?
1、外键 外键是用来让两张表的数据之间建立联系,从而保证数据的一致性和完整性。 注意,父表被关联的字段类型,必须和子表被关联的字段类型一致。 2、实际操作 (1)初始化两张表格: 子表: 父…...
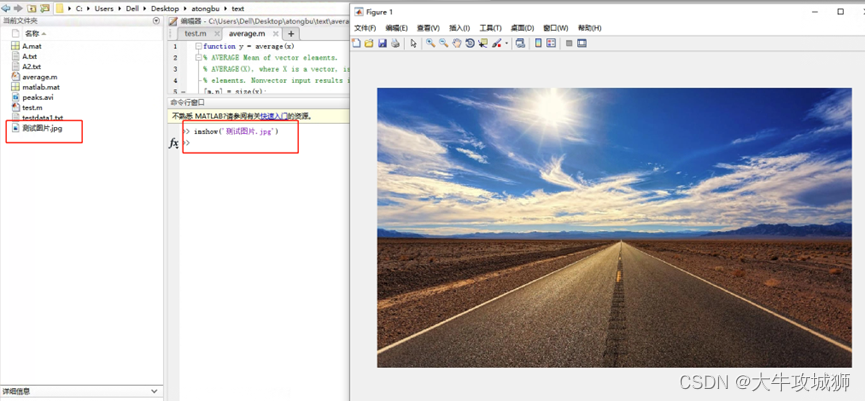
图像文件的操作MATLAB基础函数使用
简介 MATLAB中的图像处理工具箱体统了一套全方位的标准算法和图形工具,用于进行图像处理、分析、可视化和算法开发。这里仅仅对常用的基础函数做个使用介绍。 查询图像文件的信息 使用如下函数 imfinfo(filename,fmt) 函数imfinfo返回一个结构体的infoÿ…...
【k8s】Kubernetes版本v1.17.3 kubesphere 3.1.1 默认用户登录失败
1.发帖: Kubernetes版本v1.17.3 kubesphere 3.11 默认用户登录失败 - KubeSphere 开发者社区 2. 问题日志: 2.1问题排查方法 : 用户无法登录 http://192.168.56.100:30880/ 2.2查看用户状态 kubectl get users [rootk8s-node1 ~]# k…...

Mysql加密功能
Mysql加密功能 InnoDB加密功能查询条件问题开启整个数据库加密 InnoDB加密功能 InnoDB是MySQL数据库引擎的一种,它提供了加密存储的功能。具体来说,InnoDB引擎支持以下两种方式的加密存储: 表级加密:InnoDB支持表级加密ÿ…...

redis-win10安装和解决清缓存报错“Error: Protocol error, got “H“ as reply type byte”
win10安装 https://github.com/microsoftarchive/redis/releases 下载最新的zip,解压,把路径加到Path里,每次直接在cmd里 redis-server.exeError: Protocol error, got “H” as reply type byte 这个报错是因为我端口写错了。。无语 D:…...

【视觉检测】电源线圈上的导线弯直与否视觉检测系统软硬件方案
检测内容 线圈上的导线弯直与否检测系统。 检测要求 检测线圈上的导线有无弯曲,弯曲度由客户自己设定。检测速度5K/8H625PCS/H。 视觉可行性分析 对样品进行了光学实验,并进行图像处理,原则上可以使用机器视觉进行测试测量…...
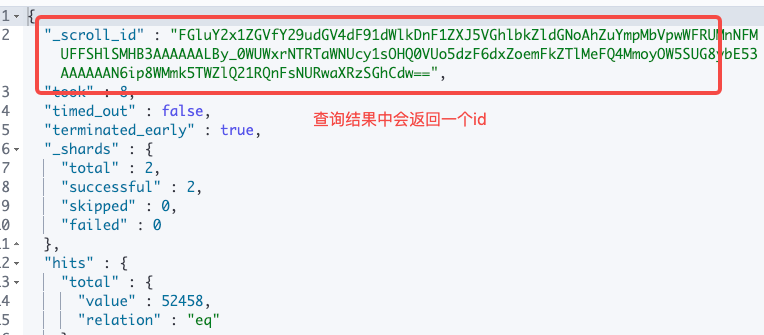
Java elasticsearch scroll模板实现
一、scroll说明和使用场景 scroll的使用场景:大数据量的检索和操作 scroll顾名思义,就是游标的意思,核心的应用场景就是遍历 elasticsearch中的数据; 通常我们遍历数据采用的是分页,elastcisearch还支持from size的…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
