算法训练营 day52 动态规划 买卖股票的最佳时机系列1
算法训练营 day52 动态规划 买卖股票的最佳时机系列1
买卖股票的最佳时机
121. 买卖股票的最佳时机 - 力扣(LeetCode)
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
确定dp数组(dp table)以及下标的含义
dp[i][0] 表示第i天持有股票所得最多现金 ,dp[i][1] 表示第i天不持有股票所得最多现金
-
确定递推公式
如果第i天持有股票即
dp[i][0], 那么可以由两个状态推出来- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:
dp[i - 1][0] - 第i天买入股票,所得现金就是买入今天的股票后所得现金即:
-prices[i]
那么
dp[i][0]应该选所得现金最大的,所以dp[i][0] = max(dp[i - 1][0], -prices[i]);如果第i天不持有股票即
dp[i][1], 也可以由两个状态推出来- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:
dp[i - 1][1] - 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:
prices[i] + dp[i - 1][0]
同样
dp[i][1]取最大的,dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]); - 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:
-
dp数组如何初始化
由递推公式
dp[i][0] = max(dp[i - 1][0], -prices[i]); 和dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出其基础都是要从dp[0][0]和dp[0][1]推导出来。那么
dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0; -
确定遍历顺序
从递推公式可以看出
dp[i]都是由dp[i - 1]推导出来的,那么一定是从前向后遍历。 -
举例推导dp数组
以示例1,输入:[7,1,5,3,6,4]为例,dp数组状态如下:

class Solution {public int maxProfit(int[] prices) {int[][] dp =new int[prices.length][2];dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i <prices.length; i++) {dp[i][0] =Math.max(dp[i-1][0],-prices[i]);dp[i][1] = Math.max(dp[i-1][1],dp[i][0]+prices[i]);}return dp[prices.length-1][1];}
}
买卖股票的最佳时机II
122. 买卖股票的最佳时机 II - 力扣(LeetCode)
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
- 第i-1天就持有股票,那么就保持现状,所得现金就是昨天持有股票的所得现金 即:
dp[i - 1][0] - 第i天买入股票,所得现金就是昨天不持有股票的所得现金减去今天的股票价格 即:
dp[i - 1][1] - prices[i]
注意这里和121. 买卖股票的最佳时机唯一不同的地方,就是推导dp[i][0]的时候,第i天买入股票的情况。
在121. 买卖股票的最佳时机中,因为股票全程只能买卖一次,所以如果买入股票,那么第i天持有股票即dp[i][0]一定就是 -prices[i]。
而本题,因为一只股票可以买卖多次,所以当第i天买入股票的时候,所持有的现金可能有之前买卖过的利润。
那么第i天持有股票即dp[i][0],如果是第i天买入股票,所得现金就是昨天不持有股票的所得现金 减去 今天的股票价格 即:dp[i - 1][1] - prices[i]。
再来看看如果第i天不持有股票即dp[i][1]的情况, 依然可以由两个状态推出来
- 第i-1天就不持有股票,那么就保持现状,所得现金就是昨天不持有股票的所得现金 即:
dp[i - 1][1] - 第i天卖出股票,所得现金就是按照今天股票价格卖出后所得现金即:
prices[i] + dp[i - 1][0]
class Solution {public int maxProfit(int[] prices) {int[][] dp = new int[prices.length][2];dp[0][0] = -prices[0];dp[0][1] = 0;for (int i = 1; i < prices.length; i++) {dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1] = Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[prices.length-1][1];}
}相关文章:

算法训练营 day52 动态规划 买卖股票的最佳时机系列1
算法训练营 day52 动态规划 买卖股票的最佳时机系列1 买卖股票的最佳时机 121. 买卖股票的最佳时机 - 力扣(LeetCode) 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票…...

3.基于分割的文本检测算法--DBNet++
文章目录1.概况2.DBNet中的主要方法2.1 网络结构2.2 适应特征图融合模块(Adaptive Scale Fusion Module, ASF)3.ASF模块的源码实现参考资料欢迎访问个人网络日志🌹🌹知行空间🌹🌹 1.概况 2022年02月份论文:Real-Time S…...

IOS打包、SDK接入记录等
IOS打包、SDK接入记录等 Mac上安装HCLR路径 /Applications/Unity/Hub/Editor/2019.4.40f1c1/Unity.app/Contents/il2cpp HCLR 指定4.40是要Unity启动打开的il2cpp,否则HCLR Installer他会报找不到MonoBleedingEdge Mac删除证书 只能点击钥匙串做上角的登录后&…...
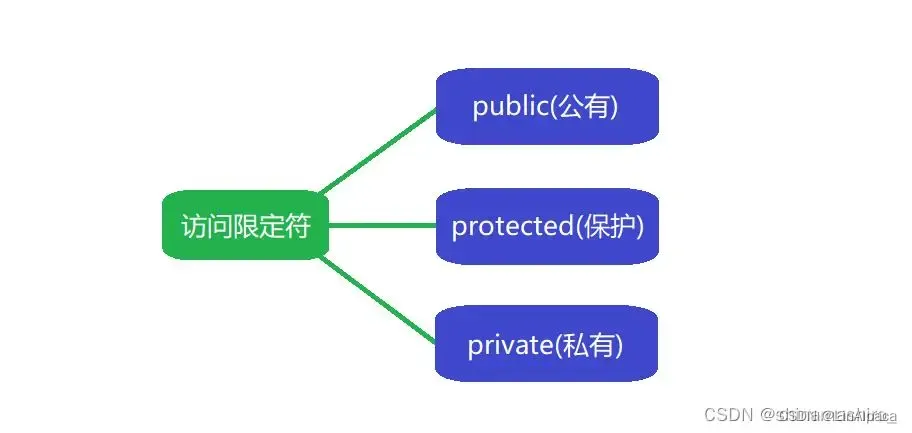
【C++】类与对象(引入)
目录 前言 类的引入 类的定义 封装与访问限定符 封装 访问限定符 类的实例化 类的大小 this指针 特性 前言 🎶我们都知道,C语言是面向过程的编程,而C是面向对象的编程,更多体现在编程的关注点上。 🎶就拿洗…...
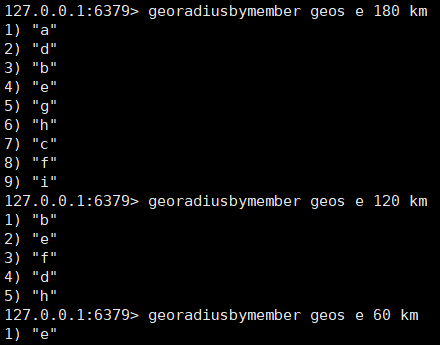
Redis 高级数据类型
文章目录一、Bitmaps:属性状态统计二、HyperLogLog:基数统计三、GEO:地理位置信息计算提示:以下是本篇文章正文内容,Redis系列学习将会持续更新 一、Bitmaps:属性状态统计 Bitmaps类型: 统计一…...

Java8 新特性-函数式接口
什么是函数式接口 先来看看传统的创建线程是怎么写的 Thread t1 new Thread(new Runnable() {Overridepublic void run() {System.out.println("t1");} }); t1.start();再来看看使用了函数式接口是怎么写的 Thread t2 new Thread(() -> System.out.println(&…...
这套软件测试试卷能打90分,直接入职字节吧
目录 一.填空 二、 判断题(正确的√,错误的╳)共10分,每小题1分 三、数据库部分:(共15分) 四、设计题。本题共 1 小题,满分 20分 一.填空 1、 系…...
GUI可视化应用开发及Python实现
0 建议学时 4学时,在机房进行 1 开发环境安装及配置 1.1 编程环境 安装PyCharm-community-2019.3.3 安装PyQt5 pip install PyQt5-tools -i https://pypi.douban.com/simple pip3 install PyQt5designer -i https://pypi.douban.com/simple1.2 环境配置 选择“…...
【论文简述】GMFlow: Learning Optical Flow via Global Matching(CVPR 2022)
一、论文简述 1. 第一作者:Haofei Xu 2. 发表年份:2022 3. 发表期刊:CVPR oral 4. 关键词:光流、代价体、Transformers、全局匹配、注意力机制 5. 探索动机:过去几年中具有代表性的光流学习框架的核心估计方式没有…...

【Spark分布式内存计算框架——离线综合实战】5. 业务报表分析
第三章 业务报表分析 一般的系统需要使用报表来展示公司的运营情况、 数据情况等,本章节对数据进行一些常见报表的开发,广告数据业务报表数据流向图如下所示: 具体报表的需求如下: 相关报表开发说明如下: 第一、数据…...

力扣-删除重复的电子邮箱
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:196. 删除重复的电子邮箱二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其…...

git基础
git-note Github Manual | GitHub Cheat Sheet | Visual Git Cheat Sheet 安装配置工具分支创建仓库.gitignore文件同步更改进行更改重做提交术语表 安装 desktop.github.com | git-scm.com 配置工具 对所有本地仓库的用户信息进行配置 对你的commit操作设置关联的用户名…...
postgres 源码解析50 LWLock轻量锁--1
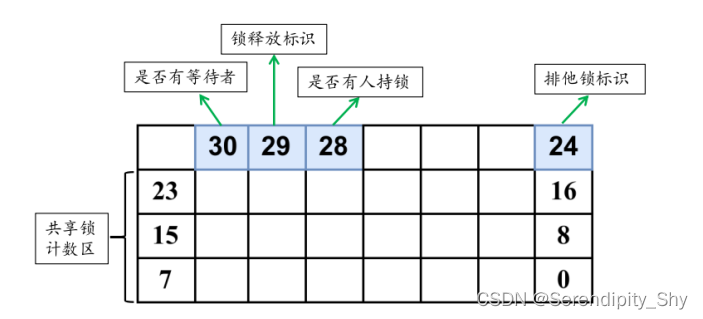
简介 postgres LWLock(轻量级锁)是由SpinLock实现,主要提供对共享存储器的数据结构的互斥访问。LWLock有两种锁模式,一种为排他模式,另一种是共享模式,如果想要读取共享内存中的内容,需要在读取…...

JVM优化常用命令
jps列出正在运行的虚拟机进程jpstop列出线程CPU或内存占用top top -Hp pid //列出pid全部线程jstat监视虚拟机运行状态信息jstat -gc pid 5000 //每隔5s打印gc情况jmapjmap -heap pid //输出jvm内存情况 jmap -histo:live pid | more //查看堆内存中的对象数量和大小 jma…...

按键中断实验
gpio.c#include"gpio.h"//给gpio使能和设置为输入模式void hal_gpio_init(){//使能GPIOF控制器RCC->MP_AHB4ENSETR|(0x1<<5);//通过GPIOF_将pf9/pf7/pf8设置为输入模式 GPIOF->MODER&(~(0x3<<18));GPIOF->MODER&(~(0x3<<14));GPI…...
kubernetes入门介绍,从0到1搭建并使用
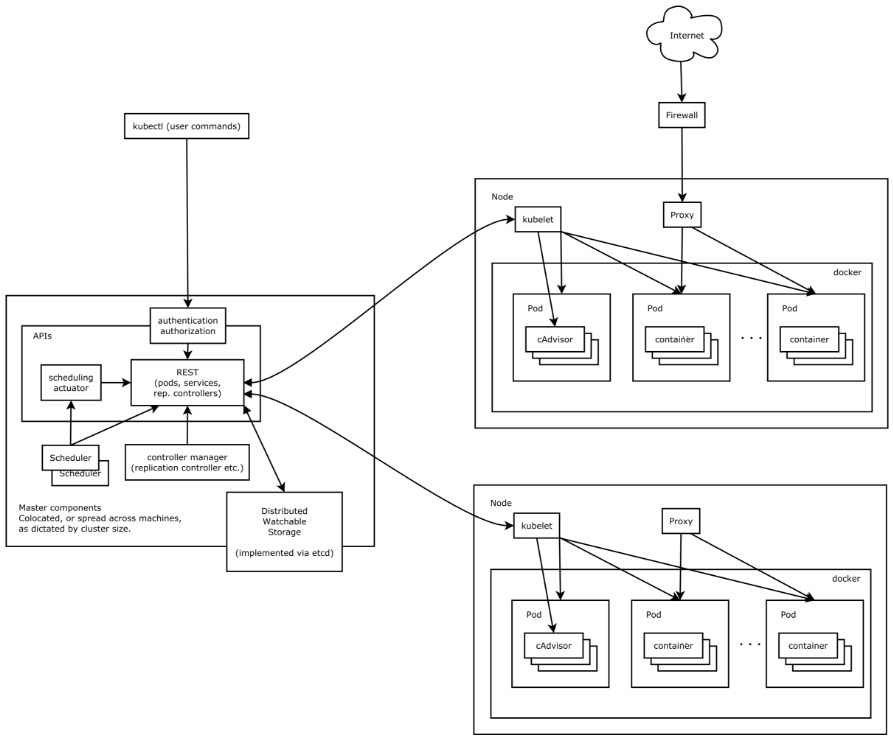
Kubernetes是一个容器编排系统,用于自动化应用程序部署、扩展和管理。本指南将介绍Kubernetes的基础知识,包括基本概念、安装部署和基础用法。 基础介绍 Kubernetes是Google开发的开源项目,是一个容器编排系统,可以自动化部署、…...

【C语言进阶】字符串函数与内存函数的学习与模拟实现
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C语言进阶 🎯长路漫漫浩浩,万事皆有期待 文章目录1.字符串处理函数介…...

【JavaEE初阶】第一节.多线程(进阶篇 ) 常见的锁策略、CAS及它的ABA问题
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、常见的锁策略 1.1 乐观锁 vs 悲观锁 1.2 普通的互斥锁 vs 读写锁 1.3 重量级锁 vs 轻量级锁 1.4 自旋锁 vs 挂起等待锁 1.5 公平…...

Linux基础命令-pstree树状显示进程信息
Linux基础命令-uname显示系统内核信息 Linux基础命令-lsof查看进程打开的文件 Linux基础命令-uptime查看系统负载 文章目录 前言 一 命令介绍 二 语法及参数 2.1 使用man查看命令语法 2.2 常用参数 三 参考实例 3.1 以树状图的形式显示所有进程 3.2 以树状图显示进程号…...
keepalived+LVS配置详解
keepalivedLVS配置详解keepalived简介keepalived的应用场景keepalived工作原理VRRP协议核心组件分层工作工作状态LVS简介LVS三种模式NAT模式(网络地址映射)IPTUN模式(IP隧道)DR模式(直接路由)三种模式对比keepalivedLVS配置1.master配置2. keepalived配置文件3 修改keepalived配…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...
