Leetcode 第 362 场周赛题解
Leetcode 第 362 场周赛题解
- Leetcode 第 362 场周赛题解
- 题目1:2848. 与车相交的点
- 思路
- 代码
- 复杂度分析
- 题目2:2849. 判断能否在给定时间到达单元格
- 思路
- 代码
- 复杂度分析
- 题目3:2850. 将石头分散到网格图的最少移动次数
- 思路
- 代码
- 复杂度分析
- 题目4:2851. 字符串转换
- 思路
- 代码
- 复杂度分析
Leetcode 第 362 场周赛题解
题目1:2848. 与车相交的点
思路
哈希。
代码
/** @lc app=leetcode.cn id=2848 lang=cpp** [2848] 与车相交的点*/// @lc code=start
class Solution
{
public:int numberOfPoints(vector<vector<int>> &nums){vector<bool> seat(101, false);for (const vector<int> &num : nums){int start = num[0], end = num[1];for (int i = start; i <= end; i++)seat[i] = true;}int count = 0;for (int i = 1; i <= 100; i++)if (seat[i])count++;return count;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n),其中 n 为数组 nums 的长度。
空间复杂度:O(L),辅助数组的长度,据题意 L = 100。
题目2:2849. 判断能否在给定时间到达单元格
思路
脑筋急转弯。
带点贪心的思想。
代码
class Solution
{
public:bool isReachableAtTime(int sx, int sy, int fx, int fy, int t){if (t == 1 && sx == fx && sy == fy)return false;return abs(sx - fx) <= t && abs(sy - fy) <= t;}
};
复杂度分析
时间复杂度:O(1)。
空间复杂度:O(1),没有辅助变量。
题目3:2850. 将石头分散到网格图的最少移动次数
思路
暴力列举全排列,每次计算出一个曼哈顿距离,更新最小值即为最小移动次数。
代码
/** @lc app=leetcode.cn id=2850 lang=cpp** [2850] 将石头分散到网格图的最少移动次数*/// @lc code=start
class Solution
{
public:int minimumMoves(vector<vector<int>> &grid){int m = grid.size(), n = m ? grid[0].size() : 0; // m = n = 3// 所有移走的石子个数 = 所有移入的石子个数(grid[i][j] = 0)vector<pair<int, int>> from; // 移走石子坐标数组vector<pair<int, int>> to; // 移入石子坐标数组// 构建 from 和 to 数组for (int i = 0; i < 3; i++)for (int j = 0; j < 3; j++){if (grid[i][j] > 1){// 有 grid[i][j] - 1 个可以移走的石子for (int k = 0; k < grid[i][j] - 1; k++)from.push_back(make_pair(i, j));}else if (grid[i][j] == 0)to.push_back(make_pair(i, j));}// 枚举 from 的全部排列可能,与 to 匹配,求 from[i] 和 to[i] 的曼哈顿距离之和,最小值即为答案int minCount = __INT_MAX__; // 最少移动次数// 使用 next_permutation 枚举全排列必须先对数组进行排序sort(from.begin(), from.end());do{int count = 0;for (int i = 0; i < from.size(); i++){// 计算曼哈顿距离count += abs(from[i].first - to[i].first) + abs(from[i].second - to[i].second);}minCount = min(minCount, count); // 更新答案} while (next_permutation(from.begin(), from.end()));return minCount;}
};
// @lc code=end
复杂度分析
时间复杂度:O(m×n×(m×n)!),使用 STL 函数 next_permutation 进行全排列的时间复杂度为O((m×n)!),循环内计算单次计算曼哈顿距离的时间复杂度为O(m×n),其中 m、n 分别为矩阵 gird 的长度和宽度,m = n = 3。
空间复杂度:O(mn),为辅助数组 from 和 to 的空间,其中 m、n 分别为矩阵 gird 的长度和宽度,m = n = 3。
题目4:2851. 字符串转换
超出能力范围。
思路
矩阵快速幂优化 DP(矩阵快速幂 + 动态规划 + KMP)
视频讲解:
https://www.bilibili.com/video/BV1U34y1N7Pe/?vd_source=df165d34990cd0aa2cacb2c452e99aad
代码
/** @lc app=leetcode.cn id=2851 lang=cpp** [2851] 字符串转换*/// @lc code=start// 矩阵快速幂优化 DPclass Solution
{
public:int numberOfWays(string s, string t, long long k){int n = s.size();int c = kmp_search(s + s.substr(0, n - 1), t);vector<vector<long long>> m = {{c - 1, c},{n - c, n - 1 - c}};m = pow(m, k);return m[0][s != t];}private:// KMP 模板vector<int> calc_max_match(string s){vector<int> match(s.size());int c = 0;for (int i = 1; i < s.size(); i++){char v = s[i];while (c && s[c] != v)c = match[c - 1];if (s[c] == v)c++;match[i] = c;}return match;}// KMP 模板// 返回 text 中出现了多少次 pattern(允许 pattern 重叠)int kmp_search(string text, string pattern){vector<int> match = calc_max_match(pattern);int match_cnt = 0, c = 0;for (int i = 0; i < text.size(); i++){char v = text[i];while (c && pattern[c] != v)c = match[c - 1];if (pattern[c] == v)c++;if (c == pattern.size()){match_cnt++;c = match[c - 1];}}return match_cnt;}const long long MOD = 1e9 + 7;// 矩阵乘法vector<vector<long long>> multiply(vector<vector<long long>> &a, vector<vector<long long>> &b){vector<vector<long long>> c(2, vector<long long>(2));for (int i = 0; i < 2; i++)for (int j = 0; j < 2; j++)c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;return c;}// 矩阵快速幂vector<vector<long long>> pow(vector<vector<long long>> &a, long long n){vector<vector<long long>> res = {{1, 0}, {0, 1}};for (; n; n /= 2){if (n % 2)res = multiply(res, a);a = multiply(a, a);}return res;}
};
// @lc code=end
复杂度分析
时间复杂度:O(n+logk),其中 n 为字符串 s 的长度。
空间复杂度:O(n),其中 n 为字符串 s 的长度。
相关文章:

Leetcode 第 362 场周赛题解
Leetcode 第 362 场周赛题解 Leetcode 第 362 场周赛题解题目1:2848. 与车相交的点思路代码复杂度分析 题目2:2849. 判断能否在给定时间到达单元格思路代码复杂度分析 题目3:2850. 将石头分散到网格图的最少移动次数思路代码复杂度分析 题目4…...
)
蓝桥杯官网练习题(0的个数)
问题描述 给定一个正整数 n ,请问 n 的十进制表示中末尾总共有几个 0 ? 输入格式 输入一行包含一个正整数 n。 输出格式 输出一个整数,表示答案。 样例输入 20220000样例输出 4评测用例规模与约定 对于所有评测用例,1 &l…...

计算线段上距离线段外某一点最近的点
一、问题 已知 p 0 = ( x 0 , y 0 ) p_0=(x_0, y_0) p...

港联证券股票分析:经济拐点显现 积极提升仓位
港联证券指出,商场底部上升的方向不变,当时稳增加和活跃资本商场的活跃方针仍在持续落地,一起也看到了一些经济数据边沿企稳的迹象,跟着方针作用的进一步闪现,商场情绪有望持续好转,上市公司基本面也有望得…...
)
不同的图像质量评价指标(IQA)
一、NR-IQA 这是一种方法不是指标 “Non-Reference Image Quality Assessment”(NR-IQA)是一种图像质量评价(Image Quality Assessment, IQA)方法,通常用于评估图像的质量,而无需使用参考图像(…...

linux命令-tar 命令
tar 命令 tar 命令一般用来打包文件 ,文件夹 , 方便传输使用. tar命令是在Linux和UNIX系统上用于创建、查看和提取tar归档文件的工具。它通常与gzip一起使用,以便在创建归档文件时进行压缩或解压缩。 -c: 创建归档文件 -x: 提取文件 -z: 告诉 tar 命令使用 gzip …...

selenium元素定位---ElementClickInterceptedException(元素点击交互异常)解决方法
1、异常原因 在编写ui自动化时,执行报错元素无法点击:ElementClickInterceptedException 具体报错:selenium.common.exceptions.ElementClickInterceptedException: Message: element click intercepted: Element <span class"el-c…...

05_css选择器的使用
一、css选择器的类型 1、标签选择器 用法:直接写 写标签名:标签名{} 示例: <!-- <!DOCTYPE html --> <html><head><meta charset"utf-8"><title>标签选择器</title><style type"te…...

跨平台游戏引擎 Axmol-2.0.0 正式发布
下载 https://github.com/axmolengine/axmol/releases/tag/v2.0.0 更新日志 添加实验性的 WebAssembly 构建支持(WebGL 2.0),由 nowasm 贡献 已知问题 WebGL context lost 尚未处理 部署在 github pages 的 demo 可快速预览,注意:由于 Git…...

面试总结归纳
面试总结 注:循序渐进,由点到面,从技术点的理解到项目中的使用, 要让面试官知道,我所知道的要比面试官更多 一、Mybatis 为ORM半持久层框架,它封装了JDBC,开发时只需要关注sql语句就可以了…...
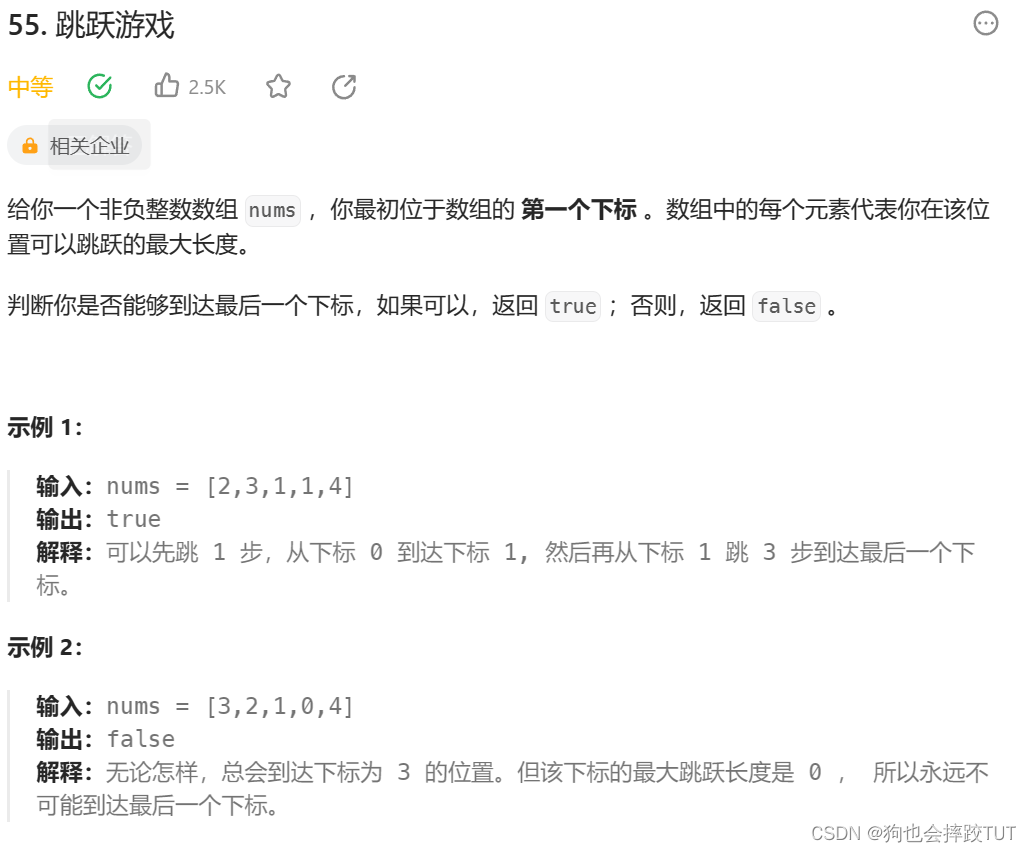
【刷题篇】贪心算法(一)
文章目录 分割平衡字符串买卖股票的最佳时机Ⅱ跳跃游戏钱币找零 分割平衡字符串 class Solution { public:int balancedStringSplit(string s) {int lens.size();int cnt0;int balance0;for(int i0;i<len;i){if(s[i]R){balance--;}else{balance;}if(balance0){cnt;}}return …...

从维基百科通过关键字爬取指定文本内容
通过输入搜索的关键字,和搜索页数范围,爬出指定文本内内容并存入到txt文档。代码逐行讲解。 使用re、res、BeautifulSoup包读取,代码已测,可以运行。txt文档内容不乱码。 import re import requests from bs4 import BeautifulS…...
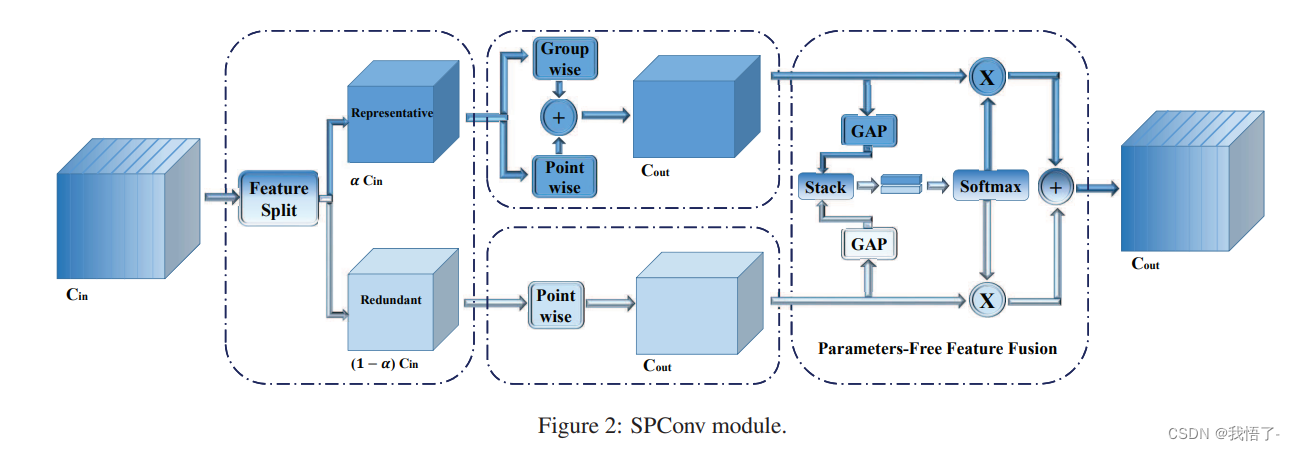
pytorch代码实现之SAConv卷积
SAConv卷积 SAConv卷积模块是一种精度更高、速度更快的“即插即用”卷积,目前很多方法被提出用于降低模型冗余、加速模型推理速度,然而这些方法往往关注于消除不重要的滤波器或构建高效计算单元,反而忽略了特征内部的模式冗余。 原文地址&am…...

一文解析-通过实例讲解 Linux 内存泄漏检测方法
一、mtrace分析内存泄露 mtrace(memory trace),是 GNU Glibc 自带的内存问题检测工具,它可以用来协助定位内存泄露问题。它的实现源码在glibc源码的malloc目录下,其基本设计原理为设计一个函数 void mtrace ()&#x…...

Spring Boot常用的参数验证技巧和使用方法
简介 Spring Boot是一个使用Java编写的开源框架,用于快速构建基于Spring的应用程序。在实际开发中,经常需要对输入参数进行验证,以确保数据的完整性和准确性。Spring Boot提供了多种方式来进行参数验证,并且可以很方便地集成到应…...

手机+卫星的科技狂想
最近硬件圈最火热的话题之一,应该就是突然上线、遥遥领先的华为Mate 60 Pro了。 其中,CPU和类5G网速是怎么实现的,是大家特别关注的问题。相比之下,卫星通话这个功能,讨论度就略低一些(没有说不火的意思&am…...
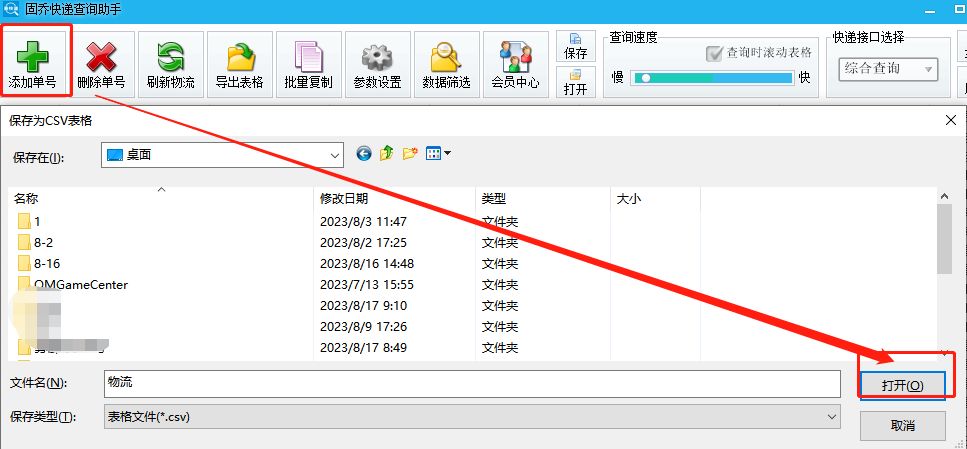
便捷查询中通快递,详细物流信息轻松获取
在如今快节奏的生活中,快递已成为人们生活中不可或缺的一部分。然而,快递查询却常常让人头疼,因为需要分别在不同的快递公司官网上进行查询,耗费时间和精力。为了解决这个问题,固乔科技推出了一款便捷的快递查询助手&a…...
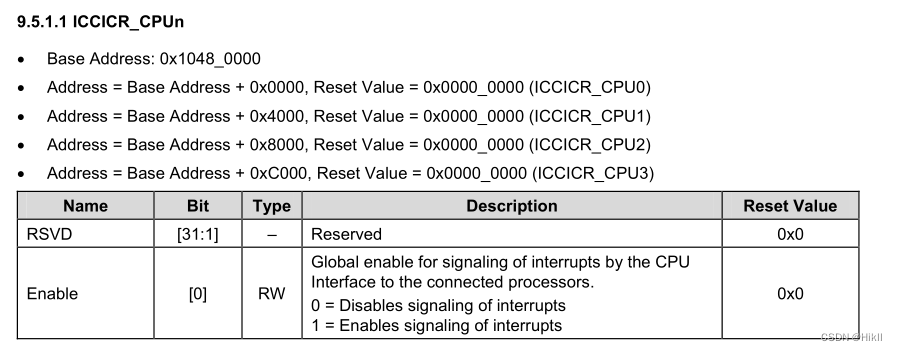
ARM接口编程—Interrupt(exynos 4412平台)
CPU与硬件的交互方式 轮询 CPU执行程序时不断地询问硬件是否需要其服务,若需要则给予其服务,若不需要一段时间后再次询问,周而复始中断 CPU执行程序时若硬件需要其服务,对应的硬件给CPU发送中断信号,CPU接收到中断信号…...
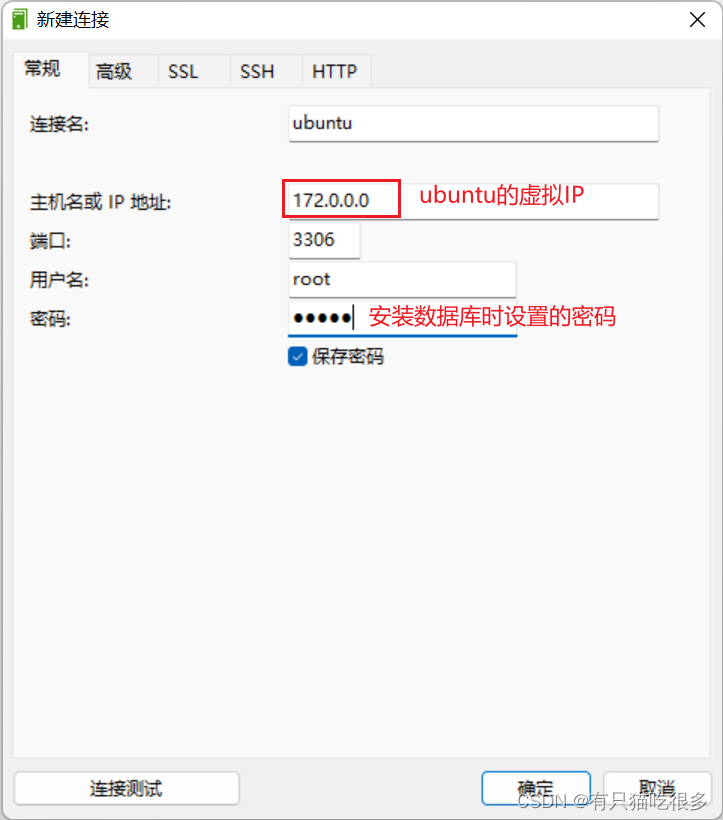
适用于Linux的Windows子系统(PHP搭建lmap、redis、swoole环境)
目录 前言 一、Windows安装Linux子系统 二、Ubuntu搭建PHP开发环境 1.PHP 安装 2.Apache2 安装 3.MySQL安装 4.Redis安装 5.Swoole安装 总结 前言 系列分为三章(从安装到项目使用): 一、适用于Linux的Windows子系统(系统安装步骤…...
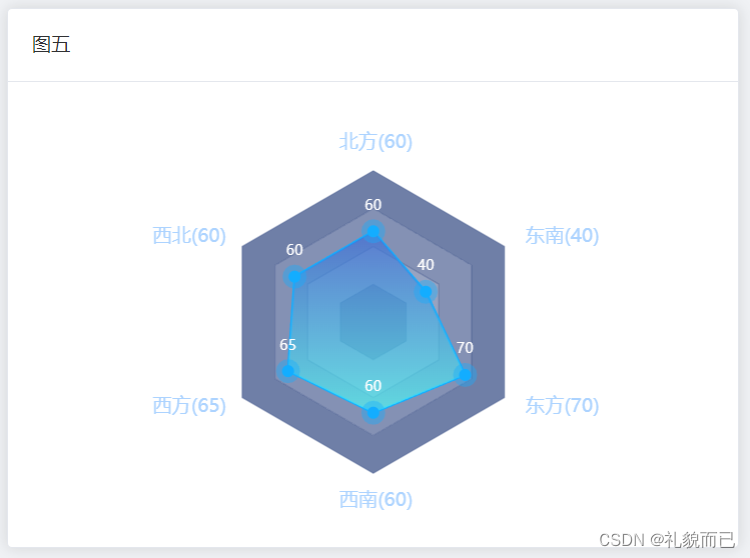
Vue3+Ts+Vite项目(第十二篇)——echarts安装与使用,vue3项目echarts组件封装
概述 技术栈:Vue3 Ts Vite Echarts 简介: 图文详解,教你如何在Vue3项目中引入Echarts,封装Echarts组件,并实现常用Echarts图例 文章目录 概述一、先看效果1.1 静态效果1.2 动态效果 二、话不多数,引入 …...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...
