day-49 代码随想录算法训练营(19) 动态规划 part 10
121.买卖股票的最佳时机
思路一:贪心
- 不断更新最小买入值
- 不断更新当前值和最小买入值的差值最大值
思路二:动态规划(今天自己写出来了哈哈哈哈哈哈哈)
- 1.dp存储:dp[i][0] 表示当前持有 dp[i][1]表示当前不持有
- 2.状态转移方程(递推式)
- dp[i][0]=max ( dp [ i - 1 ] [ 0 ] , - prices [ i ] ) 之前就持有/当前买入
- dp[i][1]=max ( dp [ i - 1 ] [ 1 ] , dp [ i - 1 ] [ 0 ] + prices [ i ] ) 之前就没持有/当前卖出
- dp[i][0]=max ( dp [ i - 1 ] [ 0 ] , - prices [ i ] ) 之前就持有/当前买入
- 3.初始化:dp[0][0]=-prices[0] dp[0][1] =0
- 4.遍历顺序:1-n
class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>>dp(n,vector<int>(2));dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<n;i++){dp[i][0]=max(dp[i-1][0],-prices[i]);dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[n-1][1];//最后肯定不持有利润最大}
};122.买卖股票的最佳时机||(拿捏)
思路一:贪心
- 只要有利润增长就卖出,最后一定获得最大利润
思路二:动态规划
1.dp存储:dp[i][0]为持有 dp[i][1]为不持有
2.状态转移方程(递推式):
- dp [ i ] [ 0 ] = max ( dp [ i - 1 ] [ 0 ] , dp [ i - 1 ] [ 1 ] - prices [ i ] ) 之前持有/现在买入(上一次不持有的金额 - 买入的金额)
- dp [ i ] [ 1 ] = max ( dp [ i - 1 ] [ 1 ] , dp [ i - 1 ] [ 0 ] + prices [ i ] ) 之前没持有/现在卖出(上一次持有的金额 + 卖出的金额)
3.初始化:dp[0][0]=-prices[0] dp[0][1]=0
4.遍历顺序:1-n
class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>>dp(n,vector<int>(2));dp[0][0]=-prices[0];dp[0][1]=0;for(int i=1;i<n;i++){dp[i][0]=max(dp[i-1][0],dp[i-1][1]-prices[i]);dp[i][1]=max(dp[i-1][1],dp[i-1][0]+prices[i]);}return dp[n-1][1];}
};123.买卖股票的最佳时机|||
思路:动态规划(5个状态)
class Solution {
public:int maxProfit(vector<int>& prices) {int n=prices.size();vector<vector<int>>dp(n,vector<int>(5,0));dp[0][1]=-prices[0];dp[0][3]=-prices[0];for(int i=1;i<n;i++){dp[i][0]=dp[i-1][0]; //第一天不持有dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i]); //第一天买入dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i]); //第一天卖出dp[i][3]=max(dp[i-1][3],dp[i-1][2]-prices[i]); //第二天买入dp[i][4]=max(dp[i-1][4],dp[i-1][3]+prices[i]);}return dp[n-1][4];}
};相关文章:
 动态规划 part 10)
day-49 代码随想录算法训练营(19) 动态规划 part 10
121.买卖股票的最佳时机 思路一:贪心 不断更新最小买入值不断更新当前值和最小买入值的差值最大值 思路二:动态规划(今天自己写出来了哈哈哈哈哈哈哈) 1.dp存储:dp[i][0] 表示当前持有 dp[i][1]表示当前不持有2.状…...

检查文件名是否含不可打印字符的C++代码源码
本篇文章属于《518抽奖软件开发日志》系列文章的一部分。 我在开发《518抽奖软件》(www.518cj.net)的时候,有时候需要检查输入的是否是合法的文件名,文件名是否含不可打印字符等。代码如下: //----------------------…...

学习笔记-正则表达式
https://www.runoob.com/regexp/regexp-tutorial.html 正则表达式re(Regular Expression)是一种文本模式,包括普通字符(例如,a 到 z 之间的字母)和特殊字符(称为"元字符"),可以用来描…...

Wireshark TS | 网络路径不一致传输丢包问题
问题背景 网络路径不一致,或者说是网络路径来回不一致,再专业点可以说是网络路径不对称,以上种种说法,做网络方向的工程师肯定会更清楚些,用简单的描述就是: A 与 B 通讯场景,C 和 D 代表中间…...

CMake高级用法实例分析(学习paddle官方的CMakeLists)
cmake基础学习教程 https://juejin.cn/post/6844903557183832078 官方完整CMakeLists cmake_minimum_required(VERSION 3.0) project(PaddleObjectDetector CXX C)option(WITH_MKL "Compile demo with MKL/OpenBlas support,defaultuseMKL." ON) o…...

数据采集: selenium 自动翻页接口调用时的验证码处理
写在前面 工作中遇到,简单整理理解不足小伙伴帮忙指正 对每个人而言,真正的职责只有一个:找到自我。然后在心中坚守其一生,全心全意,永不停息。所有其它的路都是不完整的,是人的逃避方式,是对大…...
IDEA安装翻译插件
IDEA安装翻译插件 File->Settings->Plugins 在Marketplace中,找到Translation,点击Install 更换翻译引擎 勾选自动翻译文档 翻译 鼠标右击->点击Translate...

DBeaver使用
一、导出表结构 二、导出数据CSV 导出数据时DBeaver并没有导出表结构,所以表结构需要额外保存; 导入数据CSV 导入数据时会因外键、字段长度导致失败;...

Nougat:一种用于科学文档OCR的Transformer 模型
随着人工智能领域的不断进步,其子领域,包括自然语言处理,自然语言生成,计算机视觉等,由于其广泛的用例而迅速获得了大量的普及。光学字符识别(OCR)是计算机视觉中一个成熟且被广泛研究的领域。它有许多用途,…...

redis八股1
参考Redis连环60问(八股文背诵版) - 知乎 (zhihu.com) 1.是什么 本质上是一个key-val数据库,把整个数据库加载到内存中操作,定期通过异步操作把数据flush到硬盘持久化。因为纯内存操作,所以性能很出色,每秒可以超过10…...

人工智能基础-趋势-架构
在过去的几周里,我花了一些时间来了解生成式人工智能基础设施的前景。在这篇文章中,我的目标是清晰概述关键组成部分、新兴趋势,并重点介绍推动创新的早期行业参与者。我将解释基础模型、计算、框架、计算、编排和矢量数据库、微调、标签、合…...
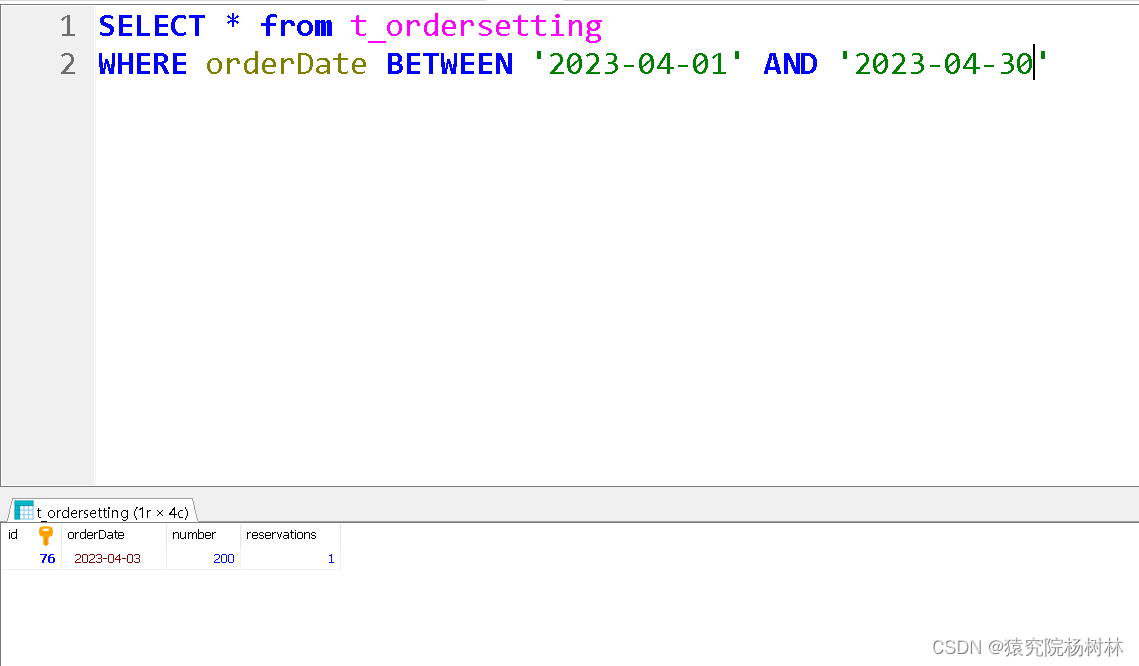
Date日期工具类(数据库日期区间问题)
文章目录 前言DateUtils日期工具类总结 前言 在我们日常开发过程中,当涉及到处理日期和时间的操作时,字符串与Date日期类往往要经过相互转换,且在SQL语句的动态查询中,往往月份的格式不正确,SQL语句执行的效果是不同的…...

为什么需要 TIME_WAIT 状态
还是用一下上一篇文章画的图 TCP 的 11 个状态,每一个状态都缺一不可,自然 TIME_WAIT 状态被赋予的意义也是相当重要,咱们直接结论先行 上文我们提到 tcp 中,主动关闭的一边会进入 TIME_WAIT 状态, 另外 Tcp 中的有 …...

Linux——(第七章)文件权限管理
目录 一、基本介绍 二、文件/目录的所有者 1.查看文件的所有者 2.修改文件所有者 三、文件/目录的所在组 1.修改文件/目录所在组 2.修改用户所在组 四、权限的基本介绍 五、rwx权限详解 1.rwx作用到文件 2.rwx作用到目录 六、修改权限 一、基本介绍 在Linux中&…...

Scala在大数据领域的崛起:当前趋势和未来前景
文章首发地址 Scala在大数据领域有着广阔的前景和现状。以下是一些关键点: Scala是一种具有强大静态类型系统的多范式编程语言,它结合了面向对象编程和函数式编程的特性。这使得Scala非常适合处理大数据,因为它能够处理并发、高吞吐量和复杂…...

前端面试经典题--页面布局
题目 假设高度已知,请写出三栏布局,其中左、右栏宽度各为300px,中间自适应。 五种解决方式代码 浮动解决方式 绝对定位解决方式 flexbox解决方式 表格布局 网格布局 源代码 <!DOCTYPE html> <html lang"en"> <…...

【webrtc】接收/发送的rtp包、编解码的VCM包、CopyOnWriteBuffer
收到的rtp包RtpPacketReceived 经过RtpDepacketizer 解析后变为ParsedPayloadRtpPacketReceived 分配内存,执行memcpy拷贝:然后把 RtpPacketReceived 给到OnRtpPacket 传递:uint8_t* media_payload = media_packet.AllocatePayload(rtx_payload.size());RTC...

Bash常见快捷键
生活在 Bash Shell 中,熟记以下快捷键,将极大的提高你的命令行操作效率。 编辑命令 Ctrl a :移到命令行首Ctrl e :移到命令行尾Ctrl f :按字符前移(右向)Ctrl b :按字符后移&a…...
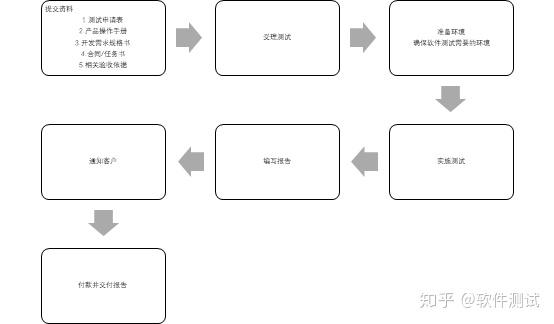
软件验收测试
1. 服务流程 验收测试 2. 服务内容 测试过程中,根据合同要求制定测试方案,验证工程项目是否满足用户需求,软件质量特性是否达到系统的要求。 3. 周期 10-15个工作日 4. 报告用途 可作为进行地方、省级、国家、部委项目的验收࿰…...

Java 与零拷贝
零拷贝是由操作系统实现的,使用 Java 中的零拷贝抽象类库在支持零拷贝的操作系统上运行才会实现零拷贝,如果在不支持零拷贝的操作系统上运行,并不会提供零拷贝的功能。 简述内核态和用户态 Linux 的体系结构分为内核态(内核空间…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

SpringCloud优势
目录 完善的微服务支持 高可用性和容错性 灵活的配置管理 强大的服务网关 分布式追踪能力 丰富的社区生态 易于与其他技术栈集成 完善的微服务支持 Spring Cloud 提供了一整套工具和组件来支持微服务架构的开发,包括服务注册与发现、负载均衡、断路器、配置管理等功能…...

npm install 相关命令
npm install 相关命令 基本安装命令 # 安装 package.json 中列出的所有依赖 npm install npm i # 简写形式# 安装特定包 npm install <package-name># 安装特定版本 npm install <package-name><version>依赖类型选项 # 安装为生产依赖(默认&…...
