leetcode分类刷题:队列(Queue)(三、优先队列用于归并排序)
1、当TopK问题出现在多个有序序列中时,就要用到归并排序的思想了
2、将优先队列初始化为添加多个有序序列的首元素的形式,再循环K次优先队列的出队和出队元素对应序列下个元素的入队,就能得到TopK的元素了
3、这些题目好像没有TopK 大用小顶堆,TopK 小用大顶堆反着来的经验了,得顺着来了:TopK 大用大顶堆,TopK 小用小顶堆
23. 合并 K 个升序链表
1、优先队列用于归并排序的经典题目:给定的有序序列为升序链表,要将所有升序链表合并成一个升序链表
2、该题直接用小顶堆实现归并排序,初始化时将所有头节点(每个有序序列的最小值)入堆,再依次弹出优先队列进行节点之间的连接;如果要直接将ListNode入堆,需要重写<,即__lt__()函数,使得节点之间能进行比较
from typing import Optional, List
import heapq
'''
23. 合并 K 个升序链表
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例 1:输入:lists = [[1,4,5],[1,3,4],[2,6]]输出:[1,1,2,3,4,4,5,6]解释:链表数组如下:[1->4->5,1->3->4,2->6]将它们合并到一个有序链表中得到。1->1->2->3->4->4->5->6
思路1、将所有链表元素全部加入优先队列(小顶堆),再依次弹出优先队列重新建立节点赋值
思路2、将链表按照(头节点值,索引,头节点)形式加入优先队列(小顶堆),再依次弹出优先队列进行节点连接——不理解为什么去掉元组里的索引就会出错
思路3、自定义节点的比较方式,直接将节点加入优先队列(小顶堆),再依次弹出优先队列进行节点连接——这叫归并?
'''class ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextclass Solution:def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:# # 思路1、将所有链表元素全部加入优先队列(小顶堆),再依次弹出优先队列重新建立节点赋值# # 情况1、数组为空# if len(lists) == None:# return None# # 情况2、将数组中所有链表添加到小顶堆# que = []# for head in lists:# if head != None:# cur = head# while cur != None:# heapq.heappush(que, cur.val)# cur = cur.next# # 继续将小顶堆的元素弹出构建为新的链表# dummyHead = ListNode(-1)# cur = dummyHead# while len(que) > 0:# cur.next = ListNode(heapq.heappop(que))# cur = cur.next# return dummyHead.next# # 思路2、将链表按照(头节点值,索引,头节点)形式加入优先队列(小顶堆),再依次弹出优先队列进行节点连接# # 情况1、数组为空# if len(lists) == None:# return None# # 情况2、将链表按照(头节点值,索引,头节点)形式加入优先队列(小顶堆)# que = []# for i in range(len(lists)):# if lists[i] != None:# heapq.heappush(que, (lists[i].val, i, lists[i]))# # 将小顶堆的节点弹出进行连接# dummyHead = ListNode(-1)# cur = dummyHead# while len(que) > 0:# _, i, head = heapq.heappop(que)# if head.next != None:# heapq.heappush(que, (head.next.val, i, head.next))# cur.next = head# cur = cur.next# return dummyHead.next# 思路3、自定义节点的比较方式,直接将节点加入优先队列(小顶堆),再依次弹出优先队列进行节点连接class Comparer:def __init__(self, node: Optional[ListNode]):self.node = nodedef __lt__(self, other):return self.node.val < other.node.val# 情况1、数组为空if len(lists) == None:return None# 情况2、将节点加入优先队列(小顶堆)que = []for head in lists:if head != None:heapq.heappush(que, Comparer(head))# 将小顶堆的节点弹出进行连接dummyHead = ListNode(-1)cur = dummyHeadwhile len(que) > 0:head = heapq.heappop(que).nodeif head.next != None:heapq.heappush(que, Comparer(head.next))cur.next = headcur = cur.nextreturn dummyHead.next
接下来的3道题目都是在leetcode分类刷题:二分查找(Binary Search)(四、基于值域的数组/矩阵类型)总结过的,当时就觉得值域二分法+双指针的思路也太复杂了,果然用归并排序的思想就要容易多了
378. 有序矩阵中第 K 小的元素
1、优先队列用于归并排序的经典题目:没有显式给定多个有序序列,需要将矩阵的每一行看作是一个个有序序列
2、该题目一开始我按照TopK 大用小顶堆,TopK 小用大顶堆反着来先用的大顶堆,并保持元素总数为K,提交后发现会超时!
3、直接用小顶堆实现归并排序,初始化时将所有矩阵第一列(每个有序序列的最小值)入堆,再循环K次小顶堆的出堆和出堆元素对应序列下个元素的入堆,循环结束就能得到第K小的元素了
4、这里题目的关键还是在于多个有序序列,循环K次小顶堆的出堆总是能保证依次出队的是最小、次小等依此类推,循环K次小顶堆的入堆也总是能保证所有有序序列各自的最小值都在堆中(除非该有序序列被访问完毕)
from typing import List
import heapq
'''
378. 有序矩阵中第 K 小的元素
题目描述:给你一个n x n矩阵matrix ,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是 排序后 的第 k 小元素,而不是第 k 个 不同 的元素。
你必须找到一个内存复杂度优于O(n2) 的解决方案。
示例 1:输入:matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8输出:13解释:矩阵中的元素为 [1,5,9,10,11,12,13,13,15],第 8 小元素是 13
题眼:Top K
思路1、优先队列(大顶堆):保持堆内元素总数为k,那么堆顶元素即为第k个最小元素
思路2、归并排序:采用优先队列(小顶堆),归并k次得到第k小的数,类似“23. 合并 K 个升序链表”
'''class Solution:def kthSmallest(self, matrix: List[List[int]], k: int) -> int:# # 思路1、优先队列(大顶堆):保持堆内元素总数为k,那么堆顶元素即为第k个最小元素# n = len(matrix)# que = []# for i in range(n):# for j in range(n):# heapq.heappush(que, -matrix[i][j]) # 添加相反数:因为python默认维护小顶堆# if len(que) > k:# heapq.heappop(que)# return -que[0]# 思路2、归并排序:采用优先队列(小顶堆),归并k次得到第k小的数,类似“23. 合并 K 个升序链表”n = len(matrix)que = []# 初始化优先队列(小顶堆)for i in range(n):heapq.heappush(que, (matrix[i][0], i, 0)) # 将每一行的最小值加入:堆顶元素为第一小的元素for _ in range(k - 1):_, i, j = heapq.heappop(que)if j + 1 <= n - 1: # 每次归并都要加入出堆序列中的最小值,保证所有排序序列各自的最小值都在堆中,直到序列为空heapq.heappush(que, (matrix[i][j + 1], i, j + 1))return heapq.heappop(que)[0]if __name__ == '__main__':obj = Solution()while True:try:in_line = input().strip().split('=')matrix = []for row in in_line[1].strip()[1: -4].split(']')[:-1]:matrix.append([int(n) for n in row.split('[')[1].split(',')])k = int(in_line[2])# print(matrix, k)print(obj.kthSmallest(matrix, k))except EOFError:break
373. 查找和最小的 K 对数字
1、优先队列用于归并排序的经典题目:没有显式给定多个有序序列,可以模拟成“378. 有序矩阵中第 K 小的元素”的矩阵形式,将nums1当作矩阵的行,nums2当作矩阵的列,再把矩阵的每一行看作是一个个有序序列
2、该题目按照值域二分+双指针需要分别添加小于小于pairSum的数对和等于pairSum的数对,非常容易出错,换成归并排序的解法就没那么繁杂了
3、这道题我也一开始我按照TopK 大用小顶堆,TopK 小用大顶堆反着来先用的大顶堆,并保持元素总数为K,提交后发现也会超时!
4、直接用小顶堆实现归并排序,初始化时将所有nums1的元素+nums[0](每个有序序列的最小值)入堆,再循环K次小顶堆的出堆和出堆元素对应序列下个元素的入堆,循环结束就能得到第K小的元素了
5、这道题目还有个细节,可能K会大于所有数对的数量,即升序返回数对就可以了,是一种不用排序的情况
6、这里题目的关键还是在于多个有序序列,循环K次小顶堆的出堆总是能保证依次出队的是最小、次小等依此类推,循环K次小顶堆的入堆也总是能保证所有有序序列各自的最小值都在堆中(除非该有序序列被访问完毕)
from typing import List
import heapq
'''
373. 查找和最小的 K 对数字
题目描述:给定两个以 升序排列 的整数数组 nums1 和 nums2,以及一个整数 k。
定义一对值(u,v),其中第一个元素来自nums1,第二个元素来自 nums2。
请找到和最小的 k个数对(u1,v1), (u2,v2) ... (uk,vk)。
示例 1:输入: nums1 = [1,7,11], nums2 = [2,4,6], k = 3输出: [1,2],[1,4],[1,6]解释: 返回序列中的前 3 对数:[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
题眼:Top K
思路1、优先队列(大顶堆):保持元素总数为k个,最终k个元素为最小的k个:会超时
思路2、归并排序:利用上两个序列是递增数组的条件,模拟成“378. 有序矩阵中第 K 小的元素”的矩阵形式,将nums1当作矩阵的行,nums2当作矩阵的列,建立优先
队列(小顶堆),归并k次得到前最k小的数
'''class Solution:def kSmallestPairs(self, nums1: List[int], nums2: List[int], k: int) -> List[List[int]]:# # 思路1、优先队列(大顶堆):保持元素总数为k个,最终k个元素为最小的k个:会超时# que = []# for n1 in nums1:# for n2 in nums2:# heapq.heappush(que, (-(n1 + n2), n1, n2)) # 大顶堆:添加相反数,因为Python默认维护小顶堆# if len(que) > k:# heapq.heappop(que)# result = [[0] for _ in range(len(que))]# for i in range(len(result) - 1, -1, -1):# _, n1, n2 = heapq.heappop(que)# result[i] = [n1, n2]# return result# 思路2、归并排序:利用上两个序列是递增数组的条件,模拟成“378. 有序矩阵中第 K 小的元素”的矩阵形式,将nums1当作矩阵的行,nums2当作矩阵的列,# 建立优先队列(小顶堆),归并k次得到前最k小的数result = []# 情况1、所有数对都要被返回:也可以把k=min(k,len(nums1)*len(nums2))合并到情况2去写if len(nums1) * len(nums2) <= k:for n1 in nums1:for n2 in nums2:result.append([n1, n2])return result# 情况2、归并k次得到前最k小的数que = []# 初始化优先队列(小顶堆)for i in range(len(nums1)):heapq.heappush(que, (nums1[i] + nums2[0], i, 0))# 归并k次得到前最k小的数for _ in range(k):_, i, j = heapq.heappop(que)result.append([nums1[i], nums2[j]])if j + 1 <= len(nums2) - 1:heapq.heappush(que, (nums1[i] + nums2[j + 1], i, j + 1))return resultif __name__ == '__main__':obj = Solution()while True:try:in_line = input().strip().split('=')nums1 = [int(n) for n in in_line[1].strip().split('[')[1].split(']')[0].split(',')]nums2 = [int(n) for n in in_line[2].strip().split('[')[1].split(']')[0].split(',')]k = int(in_line[3])# print(nums1, nums2, k)print(obj.kSmallestPairs(nums1, nums2, k))except EOFError:break
719. 找出第 K 小的数对距离
1、优先队列用于归并排序的经典题目:没有显式给定多个有序序列,可以模拟成以索引0~len(nums)-2为距离起点的len(nums)-1个有序序列,每个序列的元素总数为len(nums)-1、len(nums)-2…1
2、这道题我也一开始我按照TopK 大用小顶堆,TopK 小用大顶堆反着来先用的大顶堆,并保持元素总数为K,提交后发现也会超时!
3、直接用小顶堆实现归并排序,初始化时将所有以索引0~len(nums)-2为距离起点的距离(每个有序序列的最小值)入堆,再循环K次小顶堆的出堆和出堆元素对应序列下个元素的入堆,循环结束就能得到第K小的元素了,最终提交后还是超时了,主要是这道题目有个比较长的测试用例,没办法,看来还是只能用值域二分+双指针了
import heapq
from typing import List
'''
719. 找出第 K 小的数对距离
题目描述:数对 (a,b) 由整数 a 和 b 组成,其数对距离定义为 a 和 b 的绝对差值。
给你一个整数数组 nums 和一个整数 k ,数对由 nums[i] 和 nums[j] 组成且满足 0 <= i < j < nums.length 。
返回 所有数对距离中 第 k 小的数对距离。
示例 1:输入:nums = [1,3,1], k = 1输出:0解释:数对和对应的距离如下:(1,3) -> 2(1,1) -> 0(3,1) -> 2距离第 1 小的数对是 (1,1) ,距离为 0 。
题眼:TopK
思路1、优先队列(大顶堆):保持堆内元素个数为K,则堆顶元素为第K小的:会超时
思路2、归并排序:优先队列(小顶堆),类似“373. 查找和最小的 K 对数字”,本题在排序后会存在len(nums)-1个升序序列,然后进行k次归并排序得到前最k小的数
'''class Solution:def smallestDistancePair(self, nums: List[int], k: int) -> int:# # 思路1、优先队列(大顶堆):保持堆内元素个数为K,则堆顶元素为第K小的:会超时# que = []# for i in range(len(nums)):# for j in range(i + 1, len(nums)):# heapq.heappush(que, -abs(nums[i] - nums[j])) # 大顶堆:添加相反数,因为Python默认维护小顶堆# if len(que) > k:# heapq.heappop(que)# return -que[0]# 思路2、归并排序:优先队列(小顶堆),类似“373. 查找和最小的 K 对数字”,本题在排序后会存在len(nums)-1个升序序列,然后进行k次归并排序# 得到前最k小的数nums.sort()que = []for i in range(len(nums) - 1): # 初始化 优先队列(小顶堆)heapq.heappush(que, (abs(nums[i] - nums[i + 1]), i, i + 1))result = 0# 归并k次得到前最k小的数for _ in range(k):result, i, j = heapq.heappop(que)if j + 1 <= len(nums) - 1:heapq.heappush(que, (abs(nums[i] - nums[j + 1]), i, j + 1))return resultif __name__ == "__main__":obj = Solution()while True:try:in_line = input().strip().split('=')nums = [int(n) for n in in_line[1].split('[')[1].split(']')[0].split(',')]k = int(in_line[2])print(obj.smallestDistancePair(nums, k))except EOFError:break
相关文章:
(三、优先队列用于归并排序))
leetcode分类刷题:队列(Queue)(三、优先队列用于归并排序)
1、当TopK问题出现在多个有序序列中时,就要用到归并排序的思想了 2、将优先队列初始化为添加多个有序序列的首元素的形式,再循环K次优先队列的出队和出队元素对应序列下个元素的入队,就能得到TopK的元素了 3、这些题目好像没有TopK 大用小顶堆…...

无线窨井水位监测仪|排水管网智慧窨井液位计安装案例
城市窨井在城市排水、雨水、污水输送等方面发挥着重要作用,是污水管网、排水管网 建设重要的组成部分。随着城镇精细化建设及人民安全防范措施水平的提高,对窨井内水位的监测提出了更高的要求,他是排水管网问题的晴雨表,窨井信息化…...

024 - STM32学习笔记 - 液晶屏控制(一) - LTDC与DMA2D初始
024- STM32学习笔记 - LTDC控制液晶屏 在学习如何控制液晶屏之前,先了解一下显示屏的分类,按照目前市场上存在的各种屏幕材质,主要分为CRT阴极射线管显示屏、LCD液晶显示屏、LED显示屏、OLED显示屏,在F429的开发板上,…...
)
Python数据容器:dict(字典、映射)
1、什么是字典 Python中的字典是通过key找到对应的Value(相当于现实生活中通过“字”找到“该字的含义” 我们前面所学习过的列表、元组、字符串以及集合都不能够提供通过某个东西找到其关联的东西的相关功能,字典可以。 例如 这里有一份成绩单…...
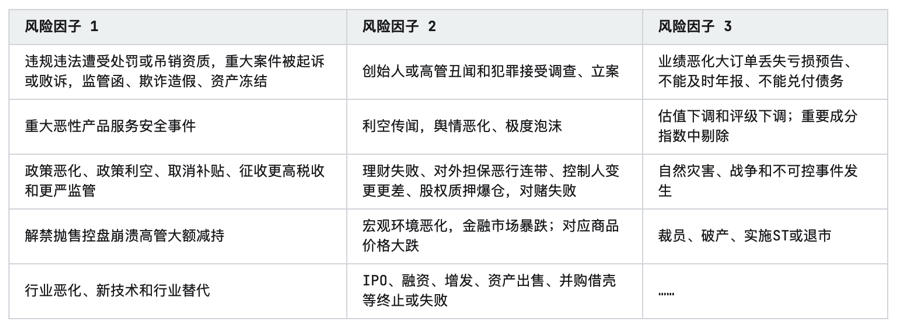
2023年基因编辑行业研究报告
第一章 行业发展概况 1.1 定义 基因编辑(Gene Editing),又称基因组编辑(Genome Editing)或基因组工程(Genome Engineering),是一项精确的科学技术,可以对含有遗传信息的…...
Spring MVC:请求转发与请求重定向
Spring MVC 请求转发请求重定向附 请求转发 转发( forward ),指服务器接收请求后,从一个资源跳转到另一个资源中。请求转发是一次请求,不会改变浏览器的请求地址。 简单示例: 1.通过 String 类型的返回值…...

按键灯待机2秒后灭掉
修改文件:/device/mediatek/mt6580/init.mt6580.rc chown system system /sys/class/leds/red/triggerchown system system /sys/class/leds/green/triggerchown system system /sys/class/leds/blue/triggerchown system system sys/devices/platform/device_info/…...

SpringBoot通过自定义注解实现日志打印
目录 前言: 正文 一.Spring AOP 1.JDK动态代理 2.Cglib动态代理 使用AOP主要的应用场景: SpringBoot通过自定义注解实现日志打印 一.Maven依赖 二.ControllerMethodLog.class自定义注解 三.Spring AOP切面方法的执行顺序 四.ControllerMethodL…...

代码随想录算法训练营第七天 |151.翻转字符串里的单词
今天是代码随想录的第七天,写了力扣的151.翻转字符串里的单词; 之后或许还要再琢磨琢磨 代码随想录链接 力扣链接 151.翻转字符串里的单词,代码如下: # class Solution: # def reverseWords(self, s: str) -> str: # …...
WEBRTC 发送视频RTP包)
【WebRTC---源码篇】(十:一)WEBRTC 发送视频RTP包
RTPSenderVideo在整个框架中起到重要的作用,它把采集的数据进行编码,并且在流程中会进行将编码后的数据进行RTP打包,最后发送到网络层 RTPSenderVideo::SendVideo //对编码数据打包 bool RTPSenderVideo::SendVideo(int payload_type,absl::optional<VideoCodecType>…...

cmd 90 validate error!(达梦数据库日志报错)
达梦数据库报错 error-cmd 90 validate error! 环境介绍1 解决办法 环境介绍 某生产环境数据库启动后,dm_实例名_202309.log,偶尔报错cmd 90 validate error! 1 解决办法 接口用错了,消息非法,比如用 6 的 JDBC 连 7 或 7 的 …...
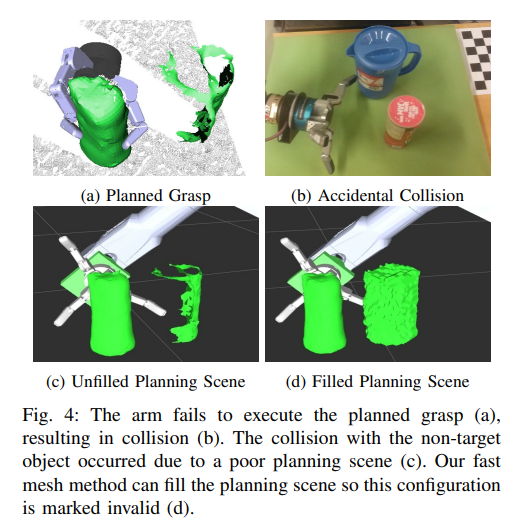
Shape Completion Enabled Robotic Grasping
摘要-这项工作提供了一个架构,使机器人能够通过形状完成抓取规划。形状完成是通过使用3D卷积神经网络(CNN)来完成的。该网络是在我们自己的新的开源数据集上训练的,该数据集包含了从不同视角捕获的超过44万个3D样本。运行时,从单个视角捕获的…...
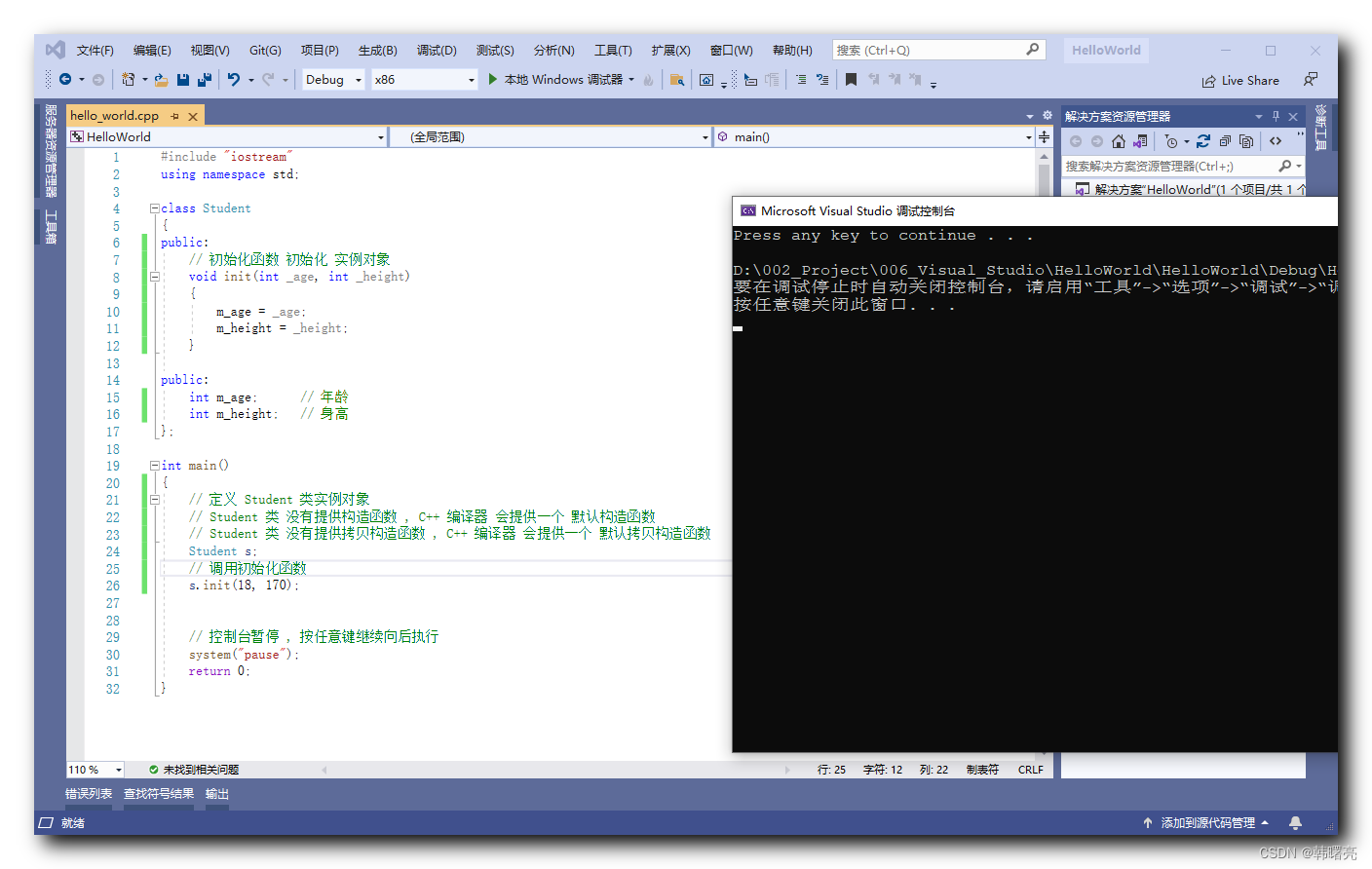
【C++】构造函数意义 ( 构造函数显式调用与隐式调用 | 构造函数替代方案 - 初始化函数 | 初始化函数缺陷 | 默认构造函数 )
文章目录 一、构造函数意义1、类的构造函数2、构造函数显式调用与隐式调用3、构造函数替代方案 - 初始化函数4、初始化函数缺陷5、默认构造函数6、代码示例 - 初始化函数无法及时调用 一、构造函数意义 1、类的构造函数 C 提供的 构造函数 和 析构函数 作为 类实例对象的 初始化…...
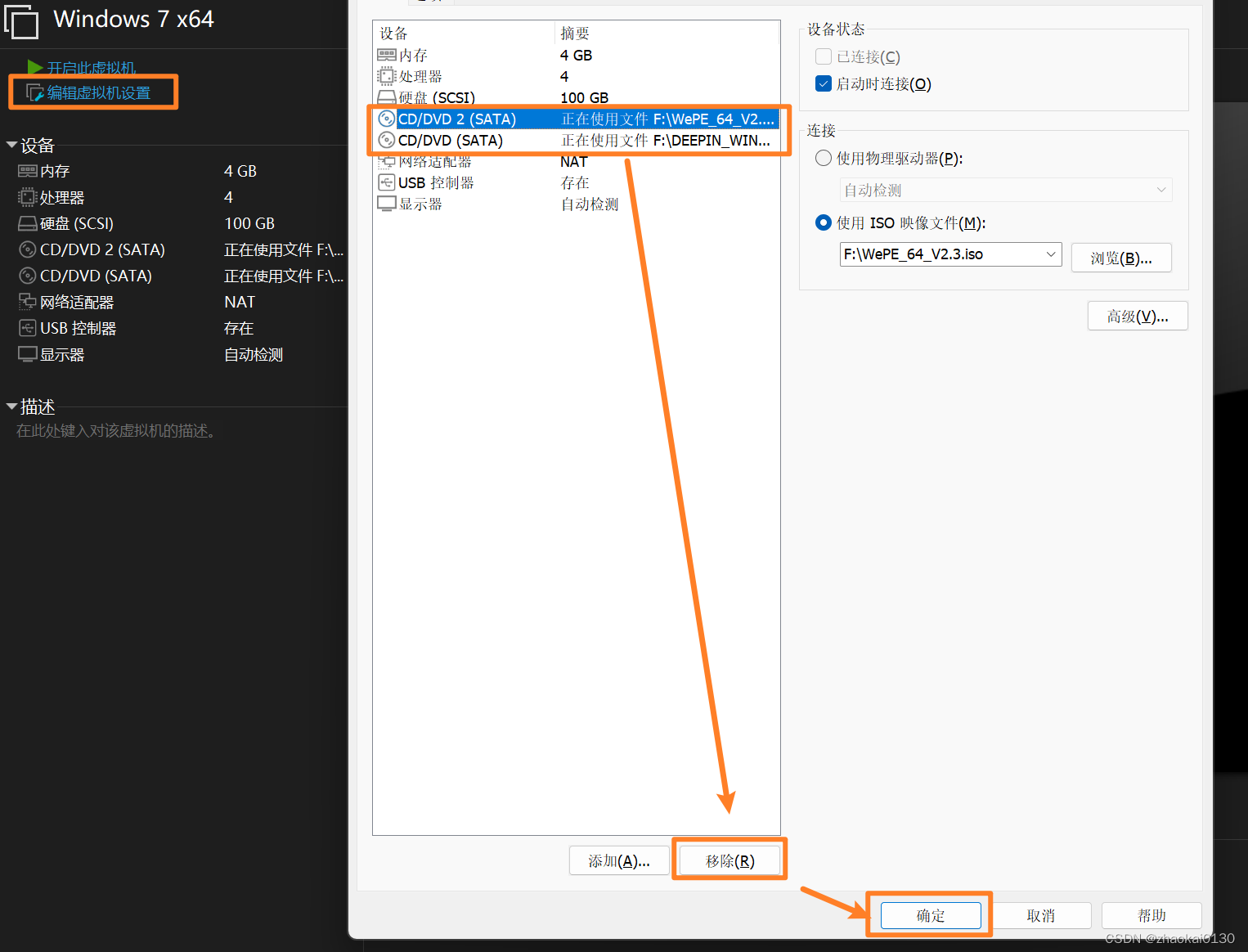
VMware16安装ghost版win7
文章目录 准备工作GHO 文件装机工具 新建虚拟机配置虚拟机还需要一个 CD/DVD PE 安装步骤分区还原挂载 CD/DVD开始还原 还原之后 准备工作 GHO 文件 可以去百度搜索这种文件,我这里是从系统之家下载的deepin win7 ghost 系统 装机工具 因为下载的 ghost 版的 w…...

项目集成swagger,访问不到swagger页面
项目集成swagger 文章目录 前言一、背景二、问题复现1.Full authentication is required to access this resource2.Illegal DefaultValue null for parameter type integer 总结 前言 项目集成swagger这个没啥好整的,maven项目就在pom文件导入依赖,ser…...
变透明的解决方案)
微信小程序怎么隐藏顶部导航栏(navigationBar)变透明的解决方案
怎么隐藏小程序顶部导航栏(navigationBar)? 官网说:Navigation是小程序的顶部导航组件,当页面配置 navigationStyle 设置为 custom 的时候可以使用此组件替代原生导航栏。 那么,我们就知道这种效果是可以…...
RabbitMQ基础概念-02
RabbitMQ是基于AMQP协议开发的一个MQ产品, 首先我们以Web管理页面为 入口,来了解下RabbitMQ的一些基础概念,这样我们后续才好针对这些基础概念 进行编程实战。 可以参照下图来理解RabbitMQ当中的基础概念: 虚拟主机 virtual hos…...

从构建者到设计者的低代码之路
低代码开发技术,是指无需编码或通过少量代码就可以快速生成应用程序的工具,一方面可降低企业应用开发人力成本和对专业软件人才的需求,另一方面可将原有数月甚至数年的开发时间成倍缩短,帮助企业实现降本增效、灵活迭代。那么&…...

Linux创建进程 及父子进程虚拟空间 多进程GDB调试
父子进程的资源是读时共享,写时拷贝,用到某一个资源,比如说改变变量的值的时候才去拷贝这个变量到一个独立的空间 父子进程的关系: 区别: 1.fork()函数的返回值不同 父进程中:>…...

uni-app 之 表格设置
uni-app 之 表格设置 image.png <view style"padding: 3%; border: #1296db;"><table style"width: 100%; border-collapse: collapse; "><tr style"height: 50px;border: 2px solid;border-color: #F7F7F7;"><td style&qu…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...
