论文阅读 (100):Simple Black-box Adversarial Attacks (2019ICML)
文章目录
- 1 概述
- 1.1 要点
- 1.2 代码
- 1.3 引用
- 2 背景
- 2.1 目标与非目标攻击
- 2.2 最小化损失
- 2.3 白盒威胁模型
- 2.4 黑盒威胁模型
- 3 简单黑盒攻击
- 3.1 算法
- 3.2 Cartesian基
- 3.3 离散余弦基
- 3.4 一般基
- 3.5 学习率 ϵ \epsilon ϵ
- 3.6 预算
1 概述
1.1 要点
题目:简单黑盒对抗攻击 (Simple black-box adversarial attacks)
策略:提出了一个在黑盒设置下构建对抗图像的简单方法:
- 从预定义的正交基中随机采样一个向量,并将其添加或减去到目标图像;
- 在多个现实任务下展示了算法的性能和效率;
- 算法非常快,且实现仅需不要20Pytorch代码;
1.2 代码
https://github.com/cg563/simple-blackbox-attack
1.3 引用
@inproceedings{Guo:2019:24842493,
author = {Guo, Chuan and Gardner, Jacob and You, Yurong and Wilson, Andrew Gordon and Weinberger, Kilian},
title = {Simple black-box adversarial attacks},
booktitle = {{ICML}},
pages = {2484--2493},
year = {2019},
url = {https://proceedings.mlr.press/v97/guo19a.html}
}
2 背景
对抗样本的研究关注于机器学习模型对细微改变的健壮性。图像分类的任务是成功预测人类所认知的图像。自然地,这样的微小改变不会影响人类的判断。基于此,可以将健壮性形式化表述为:给定一个模型 h h h和一些输入-标签对 ( x , y ) (x,y) (x,y),如果模型能正确分类 h ( x ) = y h(x)=y h(x)=y,则称 h h h是关于概率度量 d ( ⋅ , ⋅ ) d(\cdot,\cdot) d(⋅,⋅)为 ρ \rho ρ健壮的:
h ( x ′ ) = y ∀ x ′ ∈ { x ′ ∣ d ( x ′ , x ) ≤ ρ } . h(x')=y\ \forall x'\in\{ x' | d(x',x) \leq \rho \}. h(x′)=y ∀x′∈{x′∣d(x′,x)≤ρ}.度量 d d d通常被近似为 L 0 , L 2 , L ∞ L_0,L_2,L_\infty L0,L2,L∞,以度量输入 x x x和扰动 x ′ x' x′之间视觉不相似性的程度。除非特别说明,本文均采用 d ( x , x ′ ) = ∥ x − x ′ ∥ 2 d(x,x')=\| x-x' \|_2 d(x,x′)=∥x−x′∥2作为感知度量。在几何上,难以察觉的变化区域被定义为一个半径 ρ \rho ρ、以 x x x为中心的超球。对抗攻击的目标便是找到一个对抗方向 δ \delta δ,使得模型对 x ′ = x + δ x'=x+\delta x′=x+δ的决策发生改变。
2.1 目标与非目标攻击
最简单的成功攻击的条件是将原始预测改变为其它任意类别 h ( x ′ ) ≠ y h(x')\neq y h(x′)=y。这便是非目标攻击。与此相应地,目标攻击的目标是对于选择的目标类 y ′ y' y′,有 h ( x ′ ) = y ′ h(x')=y' h(x′)=y′。为了简便,余下的讨论均在目标攻击下进行。
2.2 最小化损失
由于模型输出离散决策,因此寻找对抗性扰动来改变模型首先是一个离散优化问题。然而,其经常定义一个代理损失 ℓ y ( ⋅ ) \ell_y(\cdot) ℓy(⋅)来度量模型 h h h将输入归类为 y y y的确信度。因此,对抗扰动问题可以被制定为最小化模型分类确信度的连续优化问题:
min δ ℓ y ( x + δ ) subject to ∥ δ ∥ 2 < ρ \min_\delta\ell_y(x+\delta) \text{ subject to }\| \delta \|_2<\rho δminℓy(x+δ) subject to ∥δ∥2<ρ当模型 h h h输出对应于每个类别的概率 p h ( ⋅ ∣ x ) p_h(\cdot|x) ph(⋅∣x)时,一个常用的对抗损失是类别 y y y的概率: ℓ y ( x ′ ) = p h ( y ∣ x ′ ) \ell_y(x')=p_h(y|x') ℓy(x′)=ph(y∣x′),其需要最小化正确分类的概率。对于目标攻击,一个选择是 ℓ y ′ ( x ′ ) = − p h ( y ′ ∣ x ′ ) \ell_{y'}(x')=-p_h(y'|x') ℓy′(x′)=−ph(y′∣x′),本质上是最大化误分类为 y ′ y' y′的概率。
2.3 白盒威胁模型
依赖于所在的应用领域,攻击者对于目标模型 h h h的知识有不同程度的了解。在白盒威胁模型下,分类器 h h h将提供给攻击者。在该设置下,一个有力的攻击策略是在对抗损失 ℓ y ( ⋅ ) \ell_y(\cdot) ℓy(⋅)下执行梯度下降或者近似理论。为了确保不易察觉的改变,一种方式是控制扰动的范数 ∥ δ ∥ 2 \|\delta\|_2 ∥δ∥2、早停,或者直接在损失优化过程中引入正则或者约束。
2.4 黑盒威胁模型
对于很多实际应用而言,白盒假设是不切实际的。例如,模型 h h h的展示形式是API,仅能够基于输入获取查询结果。对于攻击者而言,黑盒模型将更具有挑战性,这是因为梯度信息将不能引导对抗方向 δ \delta δ,且每次查询将消耗时间和金钱。因此,黑盒威胁设置下,附加了最小化查询次数 h h h的优化目标。修改后的优化目标为:
min δ ℓ y ( x + δ ) subject to: ∥ δ ∥ < ρ , queries ≤ B \min_\delta\ell_y(x+\delta)\text{ subject to: }\|\delta\|<\rho,\text{ queries}\leq B δminℓy(x+δ) subject to: ∥δ∥<ρ, queries≤B其中 B B B是固定代价。对于迭代优化算法而言,攻击算法需要快速收敛到可行解。
3 简单黑盒攻击
假设已有一张图像 x x x、黑盒神经网络 h h h,分类器 h ( x ) = y h(x)=y h(x)=y。我们的目标是找到一个小的扰动 δ \delta δ,其满足 h ( x + δ ) ≠ y h(x+\delta)\neq y h(x+δ)=y。尽管在黑盒设置下,梯度信息是缺失的,输出概率依然可以用于引导对抗图像的生成。
3.1 算法
算法1展示了本文输入的伪代码:对于任意方向 q \mathbf{q} q和步长大小 ϵ \epsilon ϵ, x + ϵ q x+\epsilon\mathbf{q} x+ϵq或者 x − ϵ q x-\epsilon\mathbf{q} x−ϵq可能会降低 p h ( y ∣ x ) p_h(y|x) ph(y∣x)。因此我们重复地随机选择方向 q \mathbf{q} q并添加或者减去它。为了最小化查询 h ( ⋅ ) h(\cdot) h(⋅)的次数,总是首先尝试添加 ϵ q \epsilon\mathbf{q} ϵq。如果概率 p h ( y ∣ x ) p_h(y|x) ph(y∣x)降低则采取该步骤,否则将减去 ϵ q \epsilon\mathbf{q} ϵq。
所提出的简单黑盒攻击 (SimBA) ,使用目标图像标签对 ( x , y ) (x,y) (x,y)作为输入,以及正交候选向量 Q Q Q和步长 ϵ > 0 \epsilon>0 ϵ>0。为了简化,我们均匀随机采样 q ∈ Q \mathbf{q}\in Q q∈Q。为了保证最大的查询效率,确保了没有两个方向将会取消或者削减对方,或者不合适地放大或者增加 δ \delta δ的范数。在 T T T次更新后,扰动的范数为 ∥ δ ∥ 2 = T ϵ \|\delta\|_2=\sqrt{T}\epsilon ∥δ∥2=Tϵ。

3.2 Cartesian基
正交搜索方向 Q Q Q的一个很自然的选择是标准基 Q = I Q=I Q=I,其对应算法在像素空间的更新方向。本质上,算法在每次更新随机选择一个像素增加或者减少,这样的攻击被称为 L 0 L_0 L0攻击,其将尽可能少的改变像素。
3.3 离散余弦基
最近的工作发现低频空间中的随机噪声更有可能是对抗性的。对此,我们将探索离散余弦变换 (DCT)。DCT是一个正交变换,其用于将2D图像空间 R d × d \mathbb{R}^{d\times d} Rd×d中的信号映射到与余弦波函数的幅度相对于的频率系数。接下来,我们将DCT提取的正交频率集合称为 Q DCT Q_\text{DCT} QDCT。完整的 Q DCT Q_\text{DCT} QDCT包含 d × d d\times d d×d个频段,我们仅保留比例 r r r的低频段,以在低频空间中生成对抗扰动。
3.4 一般基
理论上,在基向量可以被高效采集的前提下,任意的正交基都能用于本文方法。这对于高分辨率数据集,例如ImageNet来说无疑是一个大的挑战,因为每一个正交基的维度是 d × d d\times d d×d。迭代采样方法,例如Gram-Schmidt不能使用,因为内存代价随采样向量的数量线性增长。因此,本文仅选用标准基向量和DCT基向量。
3.5 学习率 ϵ \epsilon ϵ
给定任意的搜索方向 Q Q Q,一些方法能够更多的降低 p h ( y ∣ x ) p_h(y|x) ph(y∣x)。此外,输出概率 p h ( y ∣ x + ϵ q ) p_h(y|x+\epsilon\mathbf{q}) ph(y∣x+ϵq)可能是非单调的。图1展示了在像素空间和DCT空间随机采样搜索方向时,输出概率随 ϵ \epsilon ϵ变化的相对情况 (ReaNet-50预测ImageNet验证集)。结果表明,概率 p h ( y ∣ x + ϵ q ) p_h(y|x+\epsilon\mathbf{q}) ph(y∣x+ϵq)的下降与 ϵ \epsilon ϵ的增长相匹配。尽管一些方向增加了正确类别的概率,该概率的预期变化为负且斜率相对较陡。这说明算法对 ϵ \epsilon ϵ的选择不敏感,其将快速降低正类别的概率。

3.6 预算
通过探索 Q Q Q的正交性,我们能够约束 δ \delta δ的范数。在每次迭代过程中,基向量将被用于加或者减,当无法改变输出概率时,则抛弃。令 α i ∈ { − ϵ , 0 , ϵ } \alpha_i\in\{-\epsilon,0,\epsilon\} αi∈{−ϵ,0,ϵ}表示在第 t t t步时的搜索方向,因此:
δ t + 1 = δ t + α t q t \delta_{t+1}=\delta_t+\alpha_t\mathbf{q}_t δt+1=δt+αtqt最终的扰动可以记作:
δ T = ∑ t = 1 T α t q t \delta_T=\sum_{t=1}^T\alpha_t\mathbf{q}_t δT=t=1∑Tαtqt因为方向 q t \mathbf{q}_t qt是正交的,对于任意的 t ≠ t ′ t\neq t' t=t′, q t ⊤ q t ′ = 0 \mathbf{q}_t^\top\mathbf{q}_{t'}=0 qt⊤qt′=0。因此,对抗扰动的 L 2 L_2 L2范数计算为:
∥ δ T ∥ 2 2 = ∥ ∑ t = 1 T α t q t ∥ 2 2 = ∑ t = 1 T ∥ α t q t ∥ 2 2 = ∑ t = 1 T α t 2 ∥ q t ∥ 2 2 ≤ T ϵ 2 \left\| \delta_T \right\|_2^2 = \left\| \sum_{t=1}^T\alpha_t\mathbf{q}_t \right\|_2^2 = \sum_{t=1}^T\left\| \alpha_t\mathbf{q}_t \right\|_2^2 = \sum_{t=1}^T\alpha_t^2\left\| \mathbf{q}_t \right\|_2^2\leq T\epsilon^2 ∥δT∥22= t=1∑Tαtqt 22=t=1∑T∥αtqt∥22=t=1∑Tαt2∥qt∥22≤Tϵ2因此,在 T T T轮迭代之后,对抗扰动的最大 L 2 L_2 L2范数为 T ϵ \sqrt{T}\epsilon Tϵ,这对于任意正交基均成立。
相关文章:

论文阅读 (100):Simple Black-box Adversarial Attacks (2019ICML)
文章目录 1 概述1.1 要点1.2 代码1.3 引用 2 背景2.1 目标与非目标攻击2.2 最小化损失2.3 白盒威胁模型2.4 黑盒威胁模型 3 简单黑盒攻击3.1 算法3.2 Cartesian基3.3 离散余弦基3.4 一般基3.5 学习率 ϵ \epsilon ϵ3.6 预算 1 概述 1.1 要点 题目:简单黑盒对抗攻…...

41 个下载免费 3D 模型的最佳网站
推荐:使用 NSDT场景编辑器 快速搭建3D应用场景 1. Pikbest Pikbest是一个设计资源平台,提供超过3万件创意艺术品。您可以在Pikbest上找到设计模板,演示幻灯片,视频和音乐等。您可以找到不同的3D模型,例如婚礼装饰&…...

SpringMVC之JSR303和拦截器
认识JSR303 JSR303是一项Java标准规范,也叫做Bean Validation规范,提供了一种JavaBean数据验证的规范方式。在SpringMVC中,可以通过引入JSR303相关的依赖,来实现数据的校验。 在使用JSR303进行校验时,需要在需要校验的…...

通过rabbitmq生成延时消息,并生成rabbitmq镜像
通过rabbitmq生成延时消息队列,并生成rabbitmq镜像 整体描述1. 使用场景2. 目前问题3. 前期准备 具体步骤1. 拉取镜像2. 运行镜像3. 安装插件4. 代码支持4.1 config文件4.2 消费监听4.2 消息生产 5. 功能测试 镜像操作1. 镜像制作2. 镜像导入 总结 整体描述 1. 使用…...

结构型模式-外观模式
隐藏系统的复杂性,并向客户端提供了一个客户端可以访问系统的接口。这种类型的设计模式属于结构型模式,它向现有的系统添加一个接口,来隐藏系统的复杂性。 这种模式涉及到一个单一的类,该类提供了客户端请求的简化方法和对现有系…...
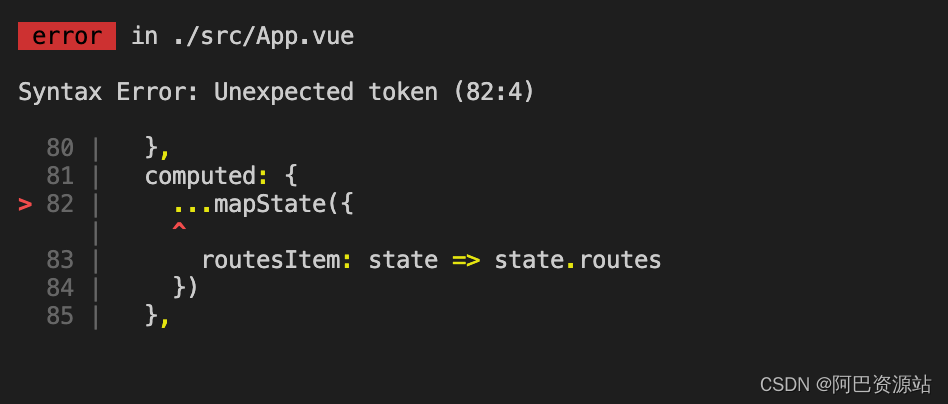
vue三个点…运算符时报错 Syntax Error: Unexpected token
出现以下问题报错: 解决: 在项目根目录新建一个名为.babelrc的文件 {"presets": ["stage-2"] }...

C# wpf 实现桌面放大镜
文章目录 前言一、如何实现?1、制作无边框窗口2、Viewbox放大3、截屏显示(1)、截屏(2)、转BitmapSource(3)、显示 4、定时截屏 二、完整代码三、效果预览总结 前言 做桌面截屏功能时需要放大镜…...

Mybatis中的#{}和${}的区别
#{}和${}他们两都是替换参数的作用,但也还是有很大区别的。 目录 一、${} 二、#{} 三、注意点 一、${} 它是直接替换过来,不添加其它的什么。 比如下面的sql语句 select *from user where id${id} 如果id1,那么他替换过来就还是1ÿ…...

选择(使用)数据库
MySQL从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article/details/129334507?spm1001.2014.3001.5502 语法格式: use 数据库名称;大家应该知道,在对数据库进行操作的时候,要制定数据库的操作对象,也就是说操作哪一个数据库 案列:选择testing数据库 …...

GFS分布式文件系统
1、GlusterFS简介 GlusterFS(GFS)是一个开源的分布式文件系统 由存储服务器、客户端以及NFS/Samba 存储网关(可选,根据需要选择使用)组成。MFS 传统的分布式文件系统大多通过元服务器来存储元数据,元数据…...

虚函数、纯虚函数、多态
一.虚函数 在基类的函数前加上virtual关键字,在派生类中重写该函数,运行时将会根据所指对象的实际类型来调用相应的函数,如果对象类型是派生类,就调用派生类的函数,如果对象类型是基类,就调用基类的函数。 …...
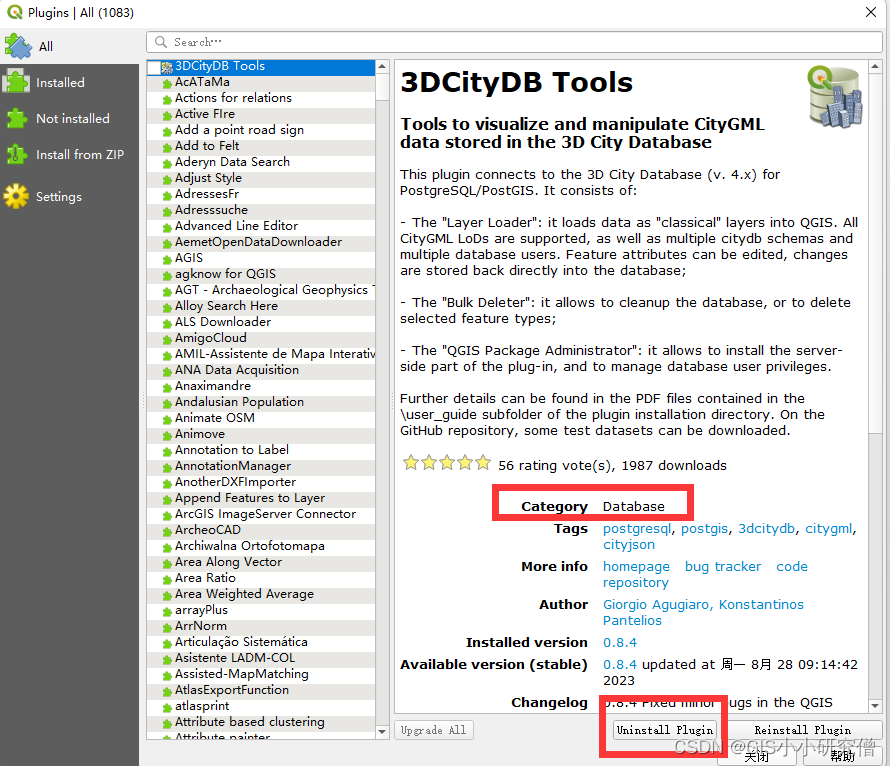
QGIS学习3 - 安装与管理插件
QGIS安装与管理插件主要是使用了菜单栏安装与管理插件这个菜单。 1、通过压缩文件等添加非官方插件 通过压缩文件添加有可能会提示存在安全问题等,直接点是即可。 之后点击install plugins即可完成。安装后导入插件 但是load失败了应该是安装没有成功。只能通过u…...

LeetCode377. 组合总和 Ⅳ
377. 组合总和 Ⅳ 文章目录 [377. 组合总和 Ⅳ](https://leetcode.cn/problems/combination-sum-iv/)一、题目二、题解方法一:完全背包一维数组动态规划思路代码分析 方法二:动态规划二维数组 一、题目 给你一个由 不同 整数组成的数组 nums ࿰…...

QT将数据写入文件,日志记录
项目场景: 在QT应用中,有时候需要将错误信息记录在log文件里面,或者需要将数据输出到文件中进行比对查看使用。 创建log文件,如果文件存在则不创建 QDir dir(QCoreApplication::applicationDirPath()"/recv_data");if(…...

vue2与vue3的使用区别与组件通信
1. 脚手架创建项目的区别: vue2: vue init webpack “项目名称”vue3: vue create “项目名称” 或者vue3一般与vite结合使用: npm create vitelatest yarn create vite2. template中结构 vue2: template下只有一个元素节点 <template><div><div…...

亚信科技与中国信通院达成全方位、跨领域战略合作
9月11日,亚信科技(中国)有限公司「简称:亚信科技」与中国信息通信研究院「简称:中国信通院」在京达成战略合作,双方将在关键技术研发、产业链协同等方面展开全方位、跨领域、跨行业深度合作,共促…...

华为Linux系统开发工程师面试
在Linux系统开发工程师的面试中,你可能会遇到以下一些问题: 在同一个网站中,当客户访问的时候,会出现有的页面访问的速度快而有的慢,系统和服务完全正常、网络带宽正常,你如何诊断这个问题?你以…...

Qt利用QTime实现sleep效果分时调用串口下发报文解决串口下发给下位机后产生的粘包问题
Qt利用QTime实现sleep效果分时调用串口下发报文解决串口下发给下位机后产生的粘包问题 文章目录 Qt利用QTime实现sleep效果分时调用串口下发报文解决串口下发给下位机后产生的粘包问题现象解决方法 现象 当有多包数据需要连续下发给下位机时,比如下载数据等&#x…...
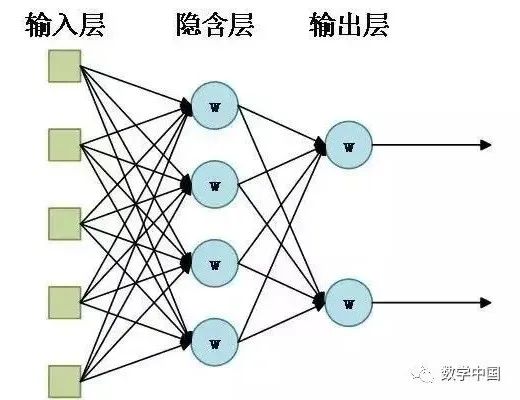
人工智能:神经细胞模型到神经网络模型
人工智能领域中的重要流派之一是:从神经细胞模型(Neural Cell Model)到神经网络模型(Neural Network Model)。 一、神经细胞模型 第一个人工神经细胞模型是“MP”模型,它是由麦卡洛克、匹茨合作࿰…...

Redisson分布式锁实战
实战来源 此问题基于电商 这周遇见这么一个问题,简略的说一下 由MQ发布了两个消息,一个是订单新增,一个是订单状态变更 由于直接付款之后,这两个消息的发布时间不分先后,可能会造成两种情况,1、订单状态变更…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
