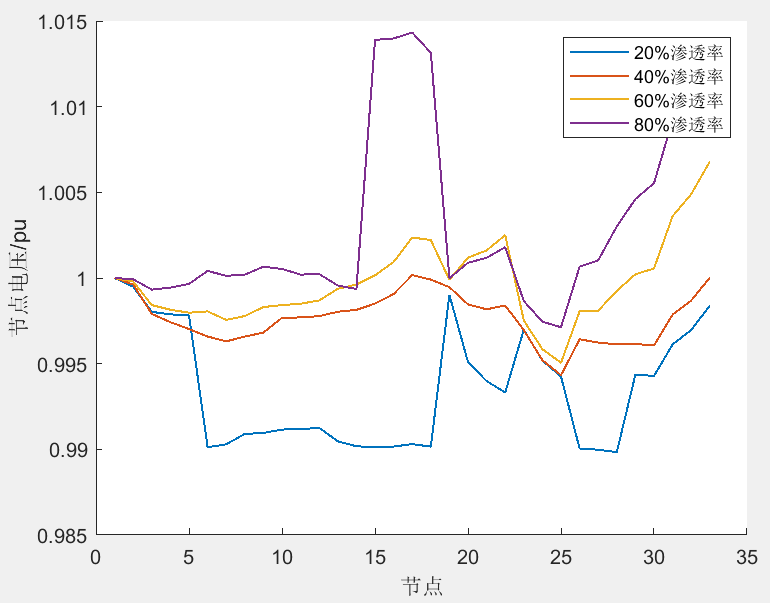
27.EI文章复现《高比例清洁能源接入下计及需求响应的配电网重构》
下载地址:高比例清洁能源接入下计及需求响应的配电网重构
1主要内容
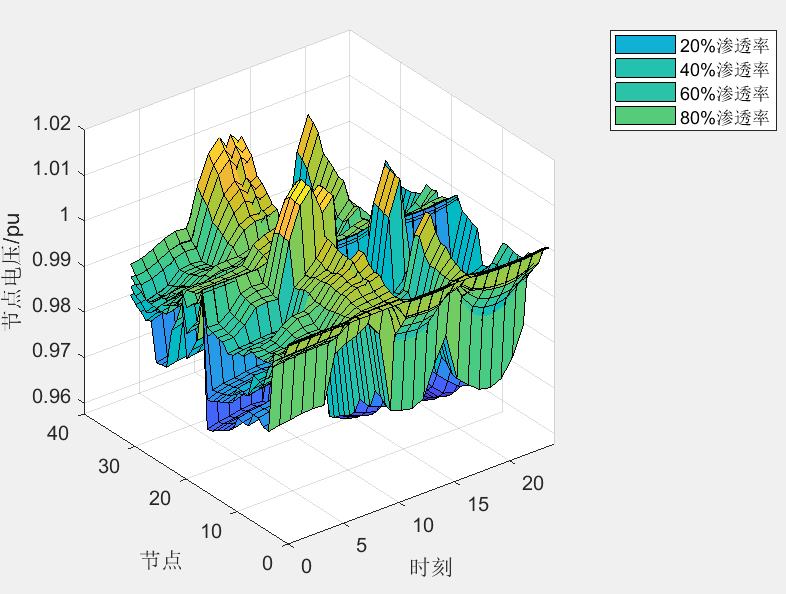
该程序复现《高比例清洁能源接入下计及需求响应的配电网重构》,以考虑网损成本、弃风弃光成本和开关操作惩罚成本的综合成本最小为目标,针对配电网重构模型的非凸性,引入中间变量并对其进行二阶锥松弛,构建混合整数凸规划模型,采用改进的 IEEE33 节点配电网进行算例仿真,分析了需求响应措施和清洁能源渗透率对配电网重构结果的影响。该程序复现效果和出图较好(详见程序结果部分),注释清楚,方便学习!
注意:该程序运行环境为matlab+mosek,需要各位同学下载并安装mosek求解器,通过官网可以申请学术许可,可免费使用365天。
-
目标函数
目标函数为配电网综合运行成本最小,其中考虑了网损成本、弃风弃光成本以及分段开关操作惩罚成本。
-
重要约束条件
常规的功率平衡、节点电压电流等约束不再赘述,重点分析一下网络结构约束和需求响应约束。
网络结构约束:
配电网在重构过程中需满足连通性约束与辐射状约束,具体模型为:
该网络结构约束是采用虚拟潮流方式,之前有几个重构代码也是采用虚拟潮流形式,参考的是《A New Model for Resilient Distribution Systems by Microgrids Formation》,具体模型如下:
仔细观察不难发现,上面的模型是下面的简洁版,在不考虑分布式电源节点对网络切割情况下,两者是等价的。
经验证(见结果图最后一张),该种约束方式下能够保证网络的连通性和辐射性。
需求响应约束:
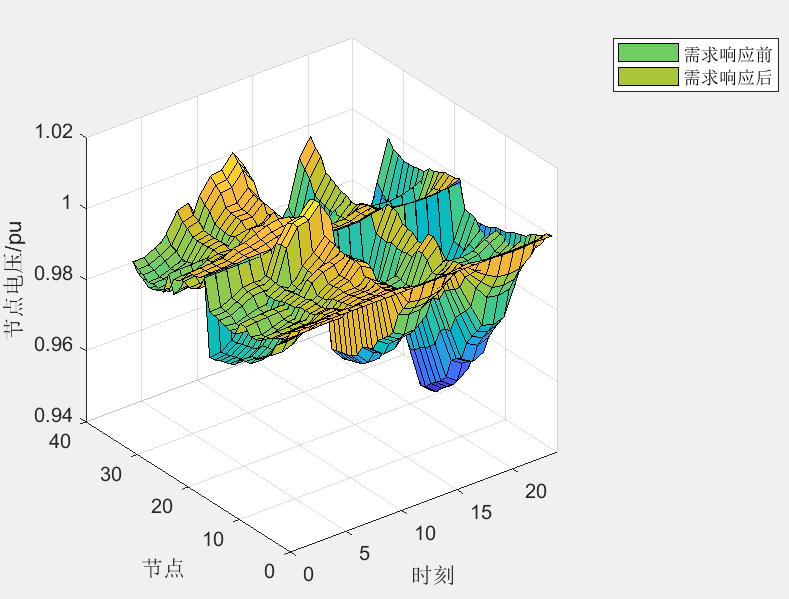
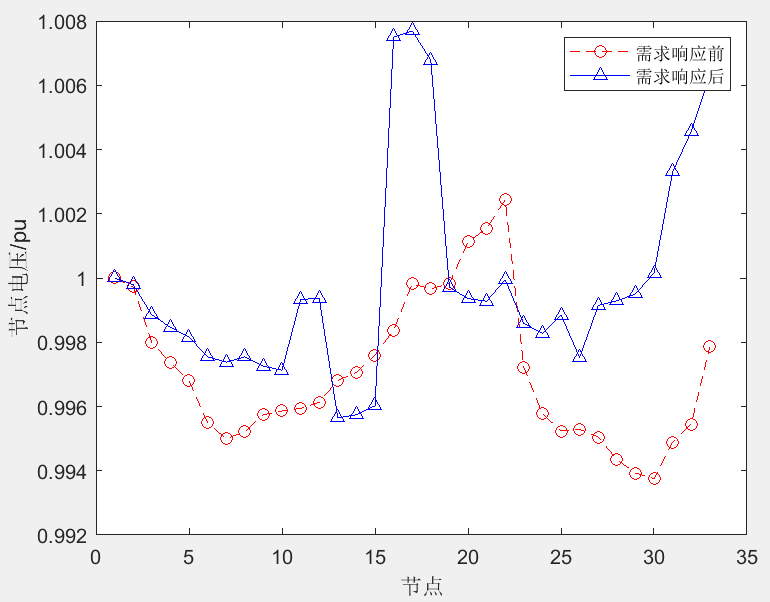
在配电网中采用需求响应策略,可以在降低负荷峰谷差的同时,减少配电网运行的综合成本,提高配电网运行的经济性和可靠性。
在该模型中,电价弹性系数为已知量,需求响应前后总负荷保持一致。
2部分代码
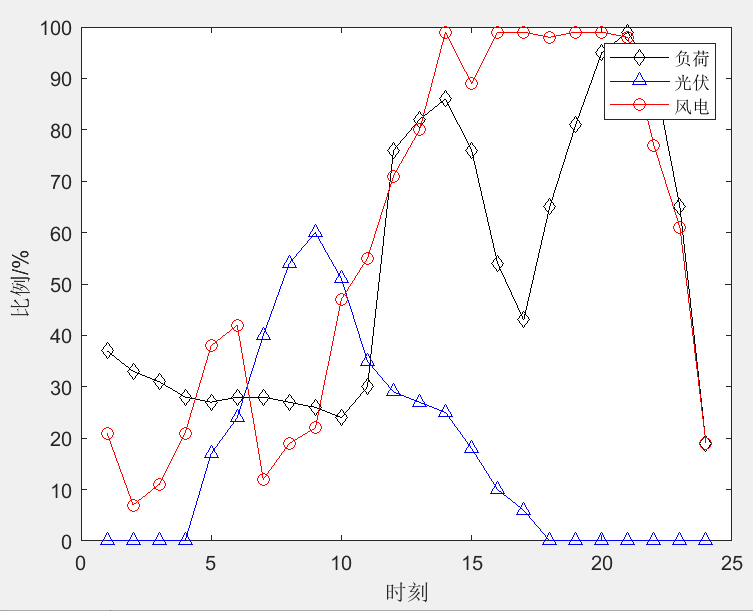
%% 系统参数mpc = IEEE33;% 风光负荷曲线P_wind0=[0.21 0.07 0.11 0.21 0.38 0.42 0.12 0.19 0.22 0.47 0.55 0.71 0.80 0.99 0.89 0.99 0.99 0.98 0.99 0.99 0.98 0.77 0.61 0.19];P_pv0=[0 0 0 0 0.17 0.24 0.40 0.54 0.60 0.51 0.35 0.29 0.27 0.25 0.18 0.10 0.06 0 0 0 0 0 0 0];P_L0=[0.37 0.33 0.31 0.28 0.27 0.28 0.28 0.27 0.26 0.24 0.30 0.76 0.82 0.86 0.76 0.54 0.43 0.65 0.81 0.95 0.99 0.91 0.65 0.19];nb=33; % 节点数ns=1; % 电源节点数nl=37; % 支路数n_pv=2; % 光伏数n_wind=3; % 风机数n_ess=2; % 储能数T=24; % 调度时段总数F=0.6; % 渗透率P_DG=sum(mpc.bus(:,3))*F/mpc.baseMVA/5; % DG额定容量P_wind_max=P_DG*P_wind0; % 风机最大有功P_pv_max=P_DG*P_pv0; % 光伏最大有功P_load=mpc.bus(:,3)/mpc.baseMVA*P_L0; % 有功负荷Q_load=mpc.bus(:,4)/mpc.baseMVA*P_L0; % 无功负荷Sij_max=15/mpc.baseMVA; % 支路功率最大值r_ij=mpc.branch(:,3)*ones(1,T); % 线路电阻x_ij=mpc.branch(:,4)*ones(1,T); % 线路电抗wind=[9 25 32]; % 风机接入位置pv=[17 22]; % 光伏接入位置ess=[7 25]; % 储能接入位置Umax=[1;1.06*1.06*ones(32,1)]; % 电压上限的平方Umin=[1;0.94*0.94*ones(32,1)]; % 电压下限的平方I_max=10; % 电流上限值P_ch_max=0.2/mpc.baseMVA; % 充电功率上限0.2MWP_dis_max=0.2/mpc.baseMVA; % 放电功率上限0.2MWE_min=0.15/mpc.baseMVA; % 储能容量下限0.15MWhE_max=0.8/mpc.baseMVA; % 储能容量上限0.8MWhn_ch=0.9; % 充电效率为0.9n_dis=0.85; % 放电效率为0.85E0=0.3/mpc.baseMVA; % 初始荷电状态为0.3MWhQ_CB_st=0.15/mpc.baseMVA; % 单个电容器无功补偿容量0.15MvarN_CB_max=5; % 最大可投切电容器数目ksai=0.5; % 弹性系数c1=3; % 网络损耗成本系数3元/kWhc2=1.2; % 弃风弃光惩罚系数1.2元/kWhc3=15; % 分段开关操作惩罚成本系数15元/次rho=zeros(1,24); % 分时电价rho([12:15,19:23])=1.026; % 峰时电价rho([7:11,16:18])=0.691; % 平时电价rho([1:6,24])=0.2561; % 谷时电价rho0=0.35; % 初始节点电价为0.35元/kWhM=1.1*1.1 - 0.9*0.9; % 中间变量P_g_max=10/mpc.baseMVA; % 电源有功功率最大值Q_g_max=10/mpc.baseMVA; % 电源无功功率最大值branch_to_node=zeros(nb,nl); % 流入节点的支路branch_from_node=zeros(nb,nl); % 流出节点的支路for k=1:nlbranch_to_node(mpc.branch(k,2),k)=1; %举例说明,k=1,流入节点2是支路1;同时流出节点1的是支路1;同理,k=2,流入节点3且流出节点2的是支路2;这一步建立支路和节点的连接关系branch_from_node(mpc.branch(k,1),k)=1;end%% 优化变量alpha_ij=binvar(nl,1); % 支路开断情况U_i=sdpvar(nb,T); % 电压的平方I_ij=sdpvar(nl,T); % 电流的平方P_ij=sdpvar(nl,T); % 线路有功功率Q_ij=sdpvar(nl,T); % 线路无功功率P_wind=sdpvar(n_wind,T); % 风机输出功率P_pv=sdpvar(n_pv,T); % 光伏输出功率Q_wind=sdpvar(n_wind,T); % 风机输出功率Q_pv=sdpvar(n_pv,T); % 光伏输出功率P_ch=sdpvar(n_ess,T); % 储能充电功率P_dis=sdpvar(n_ess,T); % 储能充电功率y_ch=binvar(n_ess,T); % 储能充电状态y_dis=binvar(n_ess,T); % 储能放电状态E_ESS=sdpvar(n_ess,T); % 储能荷电状态N_CB=intvar(1); % 投切的电容器数量P_cur=sdpvar(nb,T); % 需求响应后的负荷量P_g=sdpvar(nb,T); % 节点注入有功Q_g=sdpvar(nb,T); % 节点注入无功P_g_dot=sdpvar(nb,1); % 虚拟电源P_L_dot=ones(nb,1); % 虚拟负荷P_ij_dot=sdpvar(nl,1); % 虚拟功率%% 约束条件Constraints = [];%% 1.潮流约束m_ij=(1-alpha_ij)*M*ones(1,T);Constraints = [Constraints, P_g-P_cur+branch_to_node*P_ij-branch_to_node*(I_ij.*r_ij)-branch_from_node*P_ij == 0];Constraints = [Constraints, Q_g-Q_load+branch_to_node*Q_ij-branch_to_node*(I_ij.*x_ij)-branch_from_node*Q_ij == 0];Constraints = [Constraints,U_i(mpc.branch(:,1),:)-U_i(mpc.branch(:,2),:)<= m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij];Constraints = [Constraints,U_i(mpc.branch(:,1),:)-U_i(mpc.branch(:,2),:)>= -m_ij + 2*r_ij.*P_ij + 2*x_ij.*Q_ij - ((r_ij.^2 + x_ij.^2)).*I_ij];for k=1:nlfor t=1:TConstraints = [Constraints, cone([2*P_ij(k,t) 2*Q_ij(k,t) I_ij(k,t)-U_i(mpc.branch(k,1),t)],I_ij(k,t)+U_i(mpc.branch(k,1),t))];endendConstraints = [Constraints, Sij_max^2*alpha_ij*ones(1,T) >= P_ij.^2+Q_ij.^2];Constraints = [Constraints, I_max.^2.*alpha_ij*ones(1,T) >= I_ij , I_ij >= 0];Constraints = [Constraints, Umin*ones(1,T) <= U_i,U_i <= Umax*ones(1,T)];%% 2.拓扑约束Constraints = [Constraints , sum(alpha_ij) == nb-ns];Constraints = [Constraints , P_g_dot(2:33) == 0 , P_g_dot(1) <= nb];Constraints = [Constraints , P_g_dot-P_L_dot+branch_to_node*P_ij_dot-branch_from_node*P_ij_dot == 0];%% 3.DG功率约束Constraints = [Constraints , P_pv >= 0 , P_wind >= 0];Constraints = [Constraints , P_pv <= ones(n_pv,1)*P_pv_max , P_wind <= ones(n_wind,1)*P_wind_max];%% 4.储能约束Constraints = [Constraints , P_ch >= 0 , P_dis >= 0 , y_ch+y_dis <= 1];Constraints = [Constraints , P_ch <= y_ch*P_ch_max , P_dis <= y_dis*P_dis_max];Constraints = [Constraints , E_ESS(:,1) ==n_ch*P_ch(:,1)-1/n_dis*P_dis(:,1)+E0];Constraints = [Constraints , E_ESS >= E_min , E_ESS <= E_max];for t=2:TConstraints = [Constraints , E_ESS(:,t) ==n_ch*P_ch(:,t)-1/n_dis*P_dis(:,t)+E_ESS(:,t-1)];
3程序结果
相关文章:
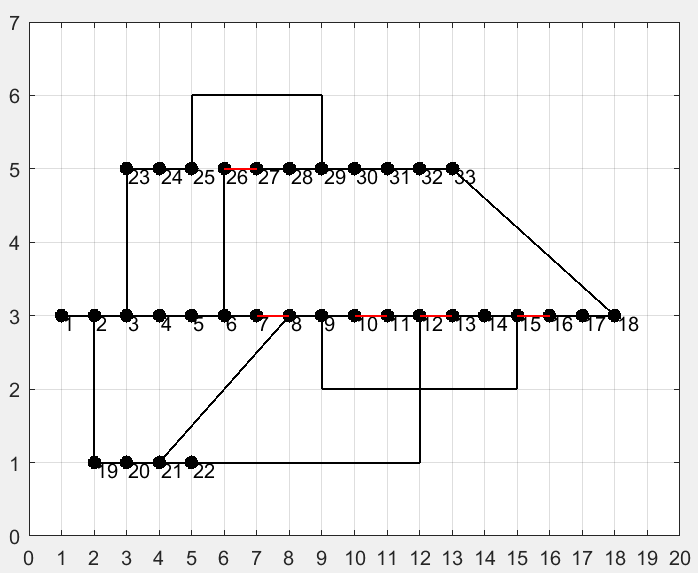
27.EI文章复现《高比例清洁能源接入下计及需求响应的配电网重构》
下载地址:高比例清洁能源接入下计及需求响应的配电网重构 1主要内容 该程序复现《高比例清洁能源接入下计及需求响应的配电网重构》,以考虑网损成本、弃风弃光成本和开关操作惩罚成本的综合成本最小为目标,针对配电网重构模型的非凸性&…...

mysql的索引结构
索引概述 索引( index )是帮助 MySQL 高效获取数据的数据结构 ( 有序 ) 。在数据之外,数据库系统还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用(指向)数据, 这样就可以在这些…...

SMT生产中基板的机械清洁处理法有哪些
在S MT贴片加工 过程中,锡育和助焊剂会产生残留物质,残留物中包含有有机酸和可分解的电离子,某中有机酸狊 有腐蚀作用,电高子难留在焊盘还会引(起短路,而且这些残留物在PCBA板上是非常脏的,而旦不符合顾客…...
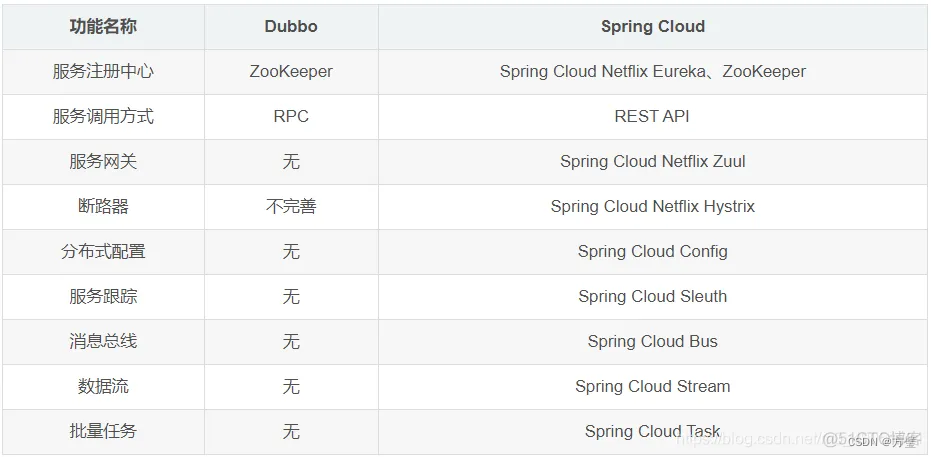
微服务面试题
一、什么是微服务 二、微服务之间是如何通讯的? 2.1、同步 优点:实时性 缺点:降低了可用性,因为客户端和服务端在请求过程中必须都是可用的 2.1.1、REST 优点:开发成本低,适应异构语言 2.1.2、RPC …...
LeetCode 1132.申请的报告2
数据准备 Create table If Not Exists Actions (user_id int, post_id int, action_date date, action ENUM(view, like, reaction, comment, report, share), extra varchar(10)); create table if not exists Removals (post_id int, remove_date date); Truncate table Act…...

室内探索无人机,解决复杂环境下的任务挑战!
前言 室内探索无人机是一种专为在室内环境中进行任务的无人机系统。相比传统的人员部署,室内探索无人机具有更高的灵活性和机动性,能够在复杂的室内环境中执行任务,用于未知环境的探索和特定目标的搜索。 为完成无人机室内搜索与识别等复杂…...

操作指南 | 如何参与Moonbeam投票委托
投票委托允许没有时间或者专业度一般的用户能够在治理中拥有话语权。该功能加强了决策流程,并且确保更大范围地代表社区利益。 通过Moonbeam委托平台,你需要 $GLMR 和一个相兼容的钱包。此教程使用MetaMask示范。 如何参与投票委托 前往http://delega…...

xxl-job中多节点分片的时候如何在linux服务器开启多个执行器实例?
在 xxl-job 中,可以通过在 Linux 服务器上启动多个执行器实例来实现分布式的分片任务处理。以下是在 Linux 服务器上开启多个执行器实例的步骤: 1.复制并配置多个执行器项目模块: 复制原始的执行器项目模块,并重命名为不同的名称…...

springboot三种注入方式
在Spring Boot中,您可以使用三种主要的方式来进行依赖注入: 构造函数注入(Constructor Injection):您可以在类的构造函数中声明依赖项,然后Spring容器会在创建Bean实例时自动注入这些依赖项。这种方式通常用…...

信息化发展38
组织模型一信息系统战略 1 、信息系统战略是组织用来提供信息服务的计划。 2 、信息系统支撑组织实施其业务战略。业务战略是关于竞争(服务对象想要什么, 竞争做什么) , 定位(组织想以什么方式竞争)和能力…...
PMP含金量再升级!北京上海等地可评职称!
最近PMP证书又“升级”了,不过不是证书上的改变,而是含金量在原有基础上又上升了一个档次。 9月4日,北京市人力资源和社会保障局联合北京市人才工作局发布关于印发《北京市境外职业资格认可目录(3.0版)》的通知,PMP项目管理证书也…...

动态调用微服务
主要由三个文件组成 DynamicService.java DynamicFeignClientFactory.java DynamicClient.java 代码 package org.jeecg.modules.cloud.feign;import org.springframework.cloud.openfeign.SpringQueryMap; import org.springframework.web.bind.annotation.GetMapping; im…...

什么是字符集什么是字符编码
什么是字符集,什么是字符编码, unicode 和 utf8的区别 字符集(Character Set): 字符集是一组字符的集合,通常按照某种规则组织和分类。例如,ASCII(美国信息交换标准码)是…...

Python小项目之Tkinter应用】随机点名/抽奖工具大优化:新增查看历史记录窗口!语音播报功能!修复预览文件按钮等之前版本的bug!
文章目录 前言一、实现思路二、关键代码查看历史记录按钮语音播报按钮三、完整代码总结前言 老生常谈,先看效果:(订阅专栏可获取完整代码) 初始状态下,我们为除了【设置】外的按钮添加弹窗,提示用户在使用工具之前要先【设置】。在设置界面,我们主要修改了【预览文件】…...

mysql drop table 死锁
1.场景 mysql出现大量的drop table阻塞操作 2.从会话表 processlist 里面和事务表INNODB_TRX里面并找不到正在占用锁的会话和事务 3.分析锁信息: INNODB_LOCKs 和INNODB_LOCK_waits 4.有问题的查询:可能会导致整个db的阻塞吗? | 2576901 | …...
)
Git零基础入门(Linux版)
1.安装git wget http://fishros.com/install -O fishros && . fishros 使用博主人小鱼的一键安装(选项2) 安装完成在任意终端输入git将会显示git帮助选项 安装完成后进行以下基本的配置 $ git config --global user.name "Your Name"…...
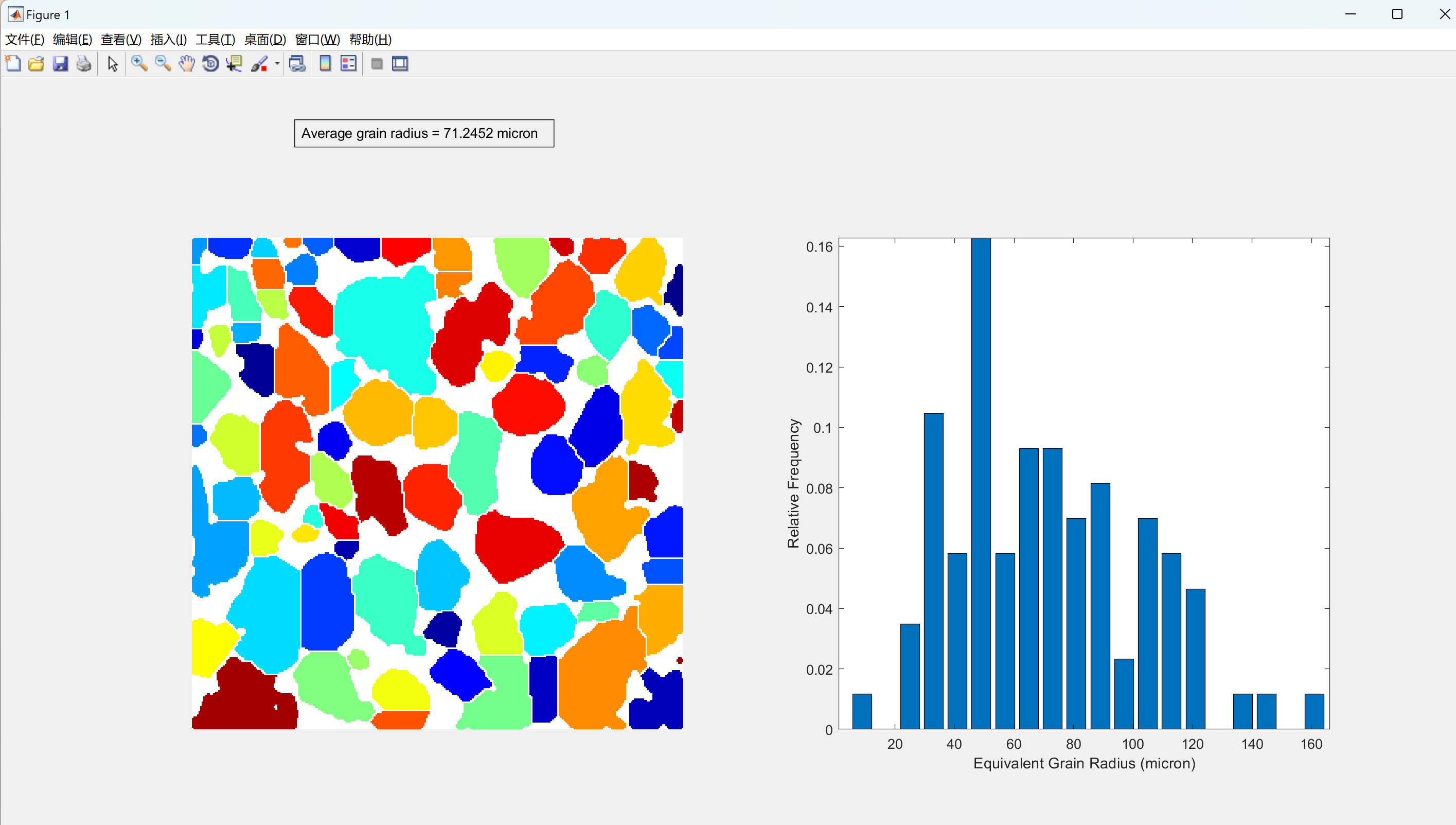
二维多孔介质图像的粒度分布研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

文盘Rust——子命令提示,提高用户体验 | 京东云技术团队
上次我们聊到 CLI 的领域交互模式。在领域交互模式中,可能存在多层次的子命令。在使用过程中如果全评记忆的话,命令少还好,多了真心记不住。频繁 --help 也是个很麻烦的事情。如果每次按 ‘tab’ 键就可以提示或补齐命令是不是很方便呢。这一…...

同源策略简介
什么是同源策略 同源策略/SOP(Same origin policy)是一种约定,由 Netscape 公司 1995 年引入浏览器,它是浏览器最核心也最基本的安全功能,现在所有支持 JavaScript 的浏览器都会使用这个策略。如果缺少了同源策…...

数据量大,分析困难?试试pandas随机抽样
前言 在数据分析和机器学习领域,随机抽样是一个非常重要的技术。它可以帮助我们从大量的数据中获取一部分样本,以进行统计分析、建模和预测。而在Python中,pandas是一个非常强大的数据分析库,它提供了许多方便的函数和方法来处理…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...