线性代数的学习和整理19,特征值,特征向量,以及引入的正交化矩阵概念(草稿)
目录
1 什么是特征值和特征向量?
1.1 特征值和特征向量这2个概念先放后
1.2 直观定义
1.3 严格定义
2 如何求特征值和特征向量
2.1 方法1:结合图形看,直观方法求
2.1.1 单位矩阵的特征值和特征向量
2.1.2 旋转矩阵
2.2 根据严格定义的公式 A*X=λ*X 来求
2.3 特征方程
2.4 互异特征值对应的特征向量之间是线性无关的
3 对角化,普通矩阵对角化为对角矩阵
2
特征值,放大伸缩倍数
特征向量,旋转角度
3.3 特征值和特征向量是什么?
直接说现在:特征向量这个块往哪个方向进行了拉伸,各个方向拉伸了几倍。这也让人很容易理解为什么,行列式的值就是特征值的乘积。
特征向量也代表了一些良好的性质,即这些线在线性变换后没有发生方向的偏移(可以逆转)只是长度发生了改变。

1 什么是特征值和特征向量?
1.1 特征值和特征向量这2个概念先放后
特征值和特征向量这2个概念先放后
先搞清楚,为什么会有特征值和特征向量
1.2 直观定义
因为有的向量,经过线性组合(线性映射)后其还是共线(方向不变/或刚好相反),这时
这些没有发生变换的向量称为特征向量
变换前后的伸缩比例叫做特征值
配图
1.3 严格定义
假设A是n阶方阵,X为非零向量,如果存在λ 使得如下等式成立
A*X=λ*X
那么λ就是A的特征值,非零向量x是A的特征向量
2 如何求特征值和特征向量
2.1 方法1:结合图形看,直观方法求
2.1.1 单位矩阵的特征值和特征向量
I*X=X
因此单位矩阵特征值是1,特征向量是向量空间内的任意向量
2.1.2 旋转矩阵
$$
\left[
\begin{matrix}
cos(θ) & -sin(θ) \\
sin(θ) & cos(θ) \\
\end{matrix}
\right]
$$
旋转矩阵需要根据,具体的转动角度θ来确定
注意θ用弧度值不要用角度值
比如θ=Π/2 不共线
θ=Π 还是共线,但是方向改变了,特征值-1 ,特征向量是所有向量?
因为任意向量来和旋转矩阵,都是刚好旋转这个弧度值
2.2 根据严格定义的公式 A*X=λ*X 来求
A*X=λ*X
A*X-λ*X=0
(A*-λ)*X=0
(A*-λ*I)*X=0
如果|A*-λ*I|≠0,那么(A*-λ*I)*X=0 只能是x=0,而x不能是零向量,因此|A*-λ*I|=0
联立方程组求解
|A*-λ*I|=0
(A*-λ*I)*X=0
|A*-λ*I|=0 → |1-λ,1 ;1 ,1-λ |=0 → (1-λ)^2-1=0
λ=0
λ=2
根据这个带入方程去求特征向量
?
2.3 特征方程
2.4 互异特征值对应的特征向量之间是线性无关的
3 对角化,普通矩阵对角化为对角矩阵
逆天 对角矩阵=[λ1,0 ; 0,λ2]
AP=P*Λ
APP-=P*Λ*P-
A=P*Λ* P-
如果P是正交矩阵,那么P-=Pt 而Pt 很好求
则A=P*Λ* Pt
相关文章:

线性代数的学习和整理19,特征值,特征向量,以及引入的正交化矩阵概念(草稿)
目录 1 什么是特征值和特征向量? 1.1 特征值和特征向量这2个概念先放后 1.2 直观定义 1.3 严格定义 2 如何求特征值和特征向量 2.1 方法1:结合图形看,直观方法求 2.1.1 单位矩阵的特征值和特征向量 2.1.2 旋转矩阵 2.2 根据严格定义…...

初步了解android如何锁键
百年三万六千日,光阴只有瞬息间。 手机下面的三个图形,正方形,园形,三角形分别的什么建?都起到什么功能? 三角形的那个叫返回键,就是可以返回你的上一个操作; 圆形是HOME键,按一下可…...
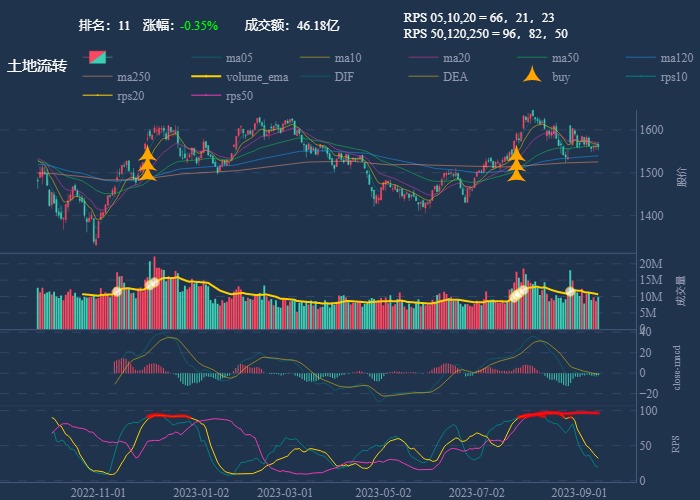
行业追踪,2023-09-13
自动复盘 2023-09-13 凡所有相,皆是虚妄。若见诸相非相,即见如来。 k 线图是最好的老师,每天持续发布板块的rps排名,追踪板块,板块来开仓,板块去清仓,丢弃自以为是的想法,板块去留让…...
)
$nextTick和setTimeout区别(宏任务微任务)
nextTick 在vue 源码中是利用 Promise.resolve()实现的。该问题实际就是Promise与setTimeout的区别,本质是Event Loop中微任务与宏任务的区别。 nextTick:在下次 DOM 更新循环结束之后执行延迟回调。在修改数据之后立即使用这个方法,获取更新后的 DOM。…...

Linux内核及可加载内核模块编程
图1 Linux系统整体结构 图2 Linux的源代码结构 下面显示一段内核模块代码案例: #include <linux/moduLe.h> #include <linux/kernel.h #include <linux/intt.h> /*模块的初始化函数lkp_ init()_init是用于初始化的修饰符 */ static int __init lk…...

软件设计师_备考笔记
考试介绍及考点分布情况 考试要求: (1)掌握数据表示、算术和逻辑运算; (2)掌握相关的应用数学、离散数学的基础知识; (3)掌握计算机体系结构以及各主要部件的性能和基…...

Java学习笔记------抽象类和抽象方法
抽象方法 抽象方法:将共性的行为(方法)抽取到父类之后,由于每一个子类执行的内容是不一样的,所以,在父类中不能确定具体的方法体,该方法就可以定义为抽象方法抽象类:如果一个类中存…...

毕业设计选题指南-25个优质选题
毕业设计是大学生活中的一项重要任务,它不仅代表了您所学知识的应用,还为未来职业道路奠定了基础。然而,许多学生常常陷入选题的困境,不知道如何选择一个合适的毕业设计题目。本文将提供一些建议,帮助您决定一个适合您…...
React使用useImperativeHandle实现父组件触发子组件事件
相关知识: useImperativeHandle forwardRef 相关代码: 获取子组件实例,由于这是函数组件,没有this因此不能整体获取,我们可以通过useImperativeHandle获取想要的变量或者方法。 父组件import React, { useRef } fro…...
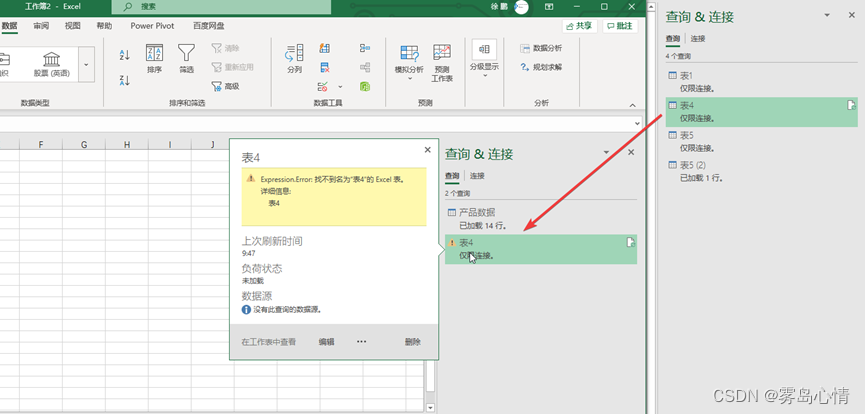
【PowerQuery】Excel的PowerQuery的复制
在Excel中构建符合要求的PowerQuery连接之后,所有的PowerQuery 连接已经顺利的保存在Excel 工作簿当中,但是如何去查看已经保存的PowerQuery连接呢?图6.3 显示了查看PowerQuery连接。 Excel界面->数据页签->查询与连接 如果你的Power…...
这个制作企业期刊的神器我怎么没早点发现
和大家分享个好消息,发现这款制作企业期刊的神器特好用 有点后悔早些没发现它,没用过的可以试试,FLBOOK在线制作电子杂志平台 下面教大家一些如何使用FLBOOK的过程 1.打开FLBOOK平台,点击登录与注册 2.点击开始制作,…...
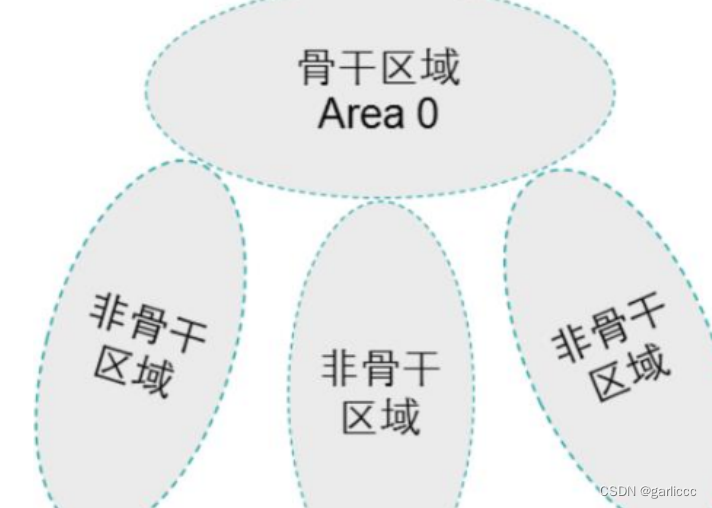
核心实验18_ospf高级_ENSP
项目场景: 核心实验18_ospf高级_ENSP 多区域虚链路 实搭拓扑图: 具体操作: R1: [R1]ospf 1 router-id 1.1.1.1 [R1-ospf-1]area 0 [R1-ospf-1-area-0.0.0.0]net 1.1.1.0 0.0.0.255 [R1-ospf-1-area-0.0.0.0]net 10.1.12.0 0.0.0.255 [R1-os…...

【python零基础入门学习】python基础篇之系统模块调用shell命令执行(四)
本站以分享各种运维经验和运维所需要的技能为主 《python》:python零基础入门学习 《shell》:shell学习 《terraform》持续更新中:terraform_Aws学习零基础入门到最佳实战 《k8》暂未更新 《docker学习》暂未更新 《ceph学习》ceph日常问题解…...

用python实现基本数据结构【01/4】
说明 如果需要用到这些知识却没有掌握,则会让人感到沮丧,也可能导致面试被拒。无论是花几天时间“突击”,还是利用零碎的时间持续学习,在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢?列表、字典、集…...

Ubuntu22.04 install Kafka
kafka quickstart install kafka...
实现JSONP请求
同源策略 JavaScript 的浏览器都会使用这个策略。所谓同源是指,域名,协议,端口相同。 而所有非同源的请求(即 域名,协议,端口 其中一种或多种不相同),都会被作为跨域请求。实际上请求…...

如何将安防视频监控系统/视频云存储EasyCVR平台推流到公网直播间?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,支持海量视频的轻量化接入与汇聚、转码与处理、全网智能分发、视频集中存储等。音视频流媒体视频平台EasyCVR拓展性强,视频能力丰富,具体可实现视频监控直播、视频轮播、视频录像、…...
使用内网负载机(Linux)执行Jmeter性能测试
一、背景 在我们工作中有时候会需要使用客户提供的内网负载机进行性能测试,一般在什么情况下我们需要要求客户提供内网负载机进行性能测试呢? 遇到公网环境下性能测试达到了带宽瓶颈。那么这时,我们就需要考虑在内网环境负载机下来执行我们…...
Web自动化测试进阶 —— Selenium模拟鼠标操作
鼠标操作事件 在实际的web产品测试中,对于鼠标的操作,不单单只有click(),有时候还要用到右击、双击、拖动等操作,这些操作包含在ActionChains类中。 ActionChains类中鼠标操作常用方法: 首先导入ActionChains类&…...

Python之函数
函数是什么? 函数是对程序逻辑进行结构化或过程化的一种编程方法,将整块代码巧妙地隔离成易于管理的小块。把重复代码放到函数中而不是进行大量的拷贝,这样既能节省空间,也有助于保持一致性;通常函数都是用于实现某一种…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

FFmpeg avformat_open_input函数分析
函数内部的总体流程如下: avformat_open_input 精简后的代码如下: int avformat_open_input(AVFormatContext **ps, const char *filename,ff_const59 AVInputFormat *fmt, AVDictionary **options) {AVFormatContext *s *ps;int i, ret 0;AVDictio…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
