数据结构基础7:二叉树【链式结构】实现和递归思想。
二叉树的链式结构实现
- 一.二叉树链式结构的实现:
- 1.前置说明:
- 1.创建二叉树:
- 2.二叉树的结构:
- 2.二叉树的遍历:
- 1.二叉树的前中后序遍历:
- 2.内容拓展:
- 二.二叉树链式(题目)
- 题目一:计算节点的个数:
- 方法一:注意事项:
- 方法二:注意事项:
- 题目二:计算叶子节点的个数:
- 方法一:
- 题目三:求第K层节点的个数:
- 方法一:
- 题目四:
- 方法一:重新定义一个函数:
- 方法二:(判断左右节点数值和root数值)
- 题目五:二叉树的最大深度:
- 方法一:
一.二叉树链式结构的实现:
1.前置说明:
对于一颗二叉树的构建是比较复杂的在刚刚开始了解二叉树的构建的时候。我们可以通过创建多个节点的方式去构建二叉树的结构,直接连接节点的左右节点构建一个二叉树方便去学习。
1.创建二叉树:
struct TreeNode* byNode(TreeNodeData x)
{struct TreeNode* tmp = (struct TreeNode*)malloc(sizeof(struct TreeNode));if (tmp == NULL){perror(tmp);exit(-1);}tmp->val = x;tmp->left = NULL;tmp->right = NULL;return tmp;
}void creatTreeNode()
{//1.构建二叉树:struct TreeNode* n1 = byNode(1);struct TreeNode* n2 = byNode(2);struct TreeNode* n3 = byNode(3);struct TreeNode* n4 = byNode(4);struct TreeNode* n5 = byNode(5);struct TreeNode* n6 = byNode(6);struct TreeNode* n7 = byNode(7);n1->left = n2;n1->right = n3;n2->left = n4;n2->right = n5;n3->left = n6;n3->right = n7;}
int main()
{//1.构建二叉树:creatTreeNode();
}
2.二叉树的结构:
1.需要注意的是上面的代码不是创建二叉树的一个正规方法,后面我的博客是会去涉及到二叉树的一个创建:
1.空树:
2.非空树:
从二叉树的概念可知二叉树是递归构建的所以后面的操作都是基于递归构建的内容。
2.二叉树的遍历:
1.二叉树的前中后序遍历:
1.学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
2.前中后序遍历递归结构遍历:
- 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
- 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
- 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
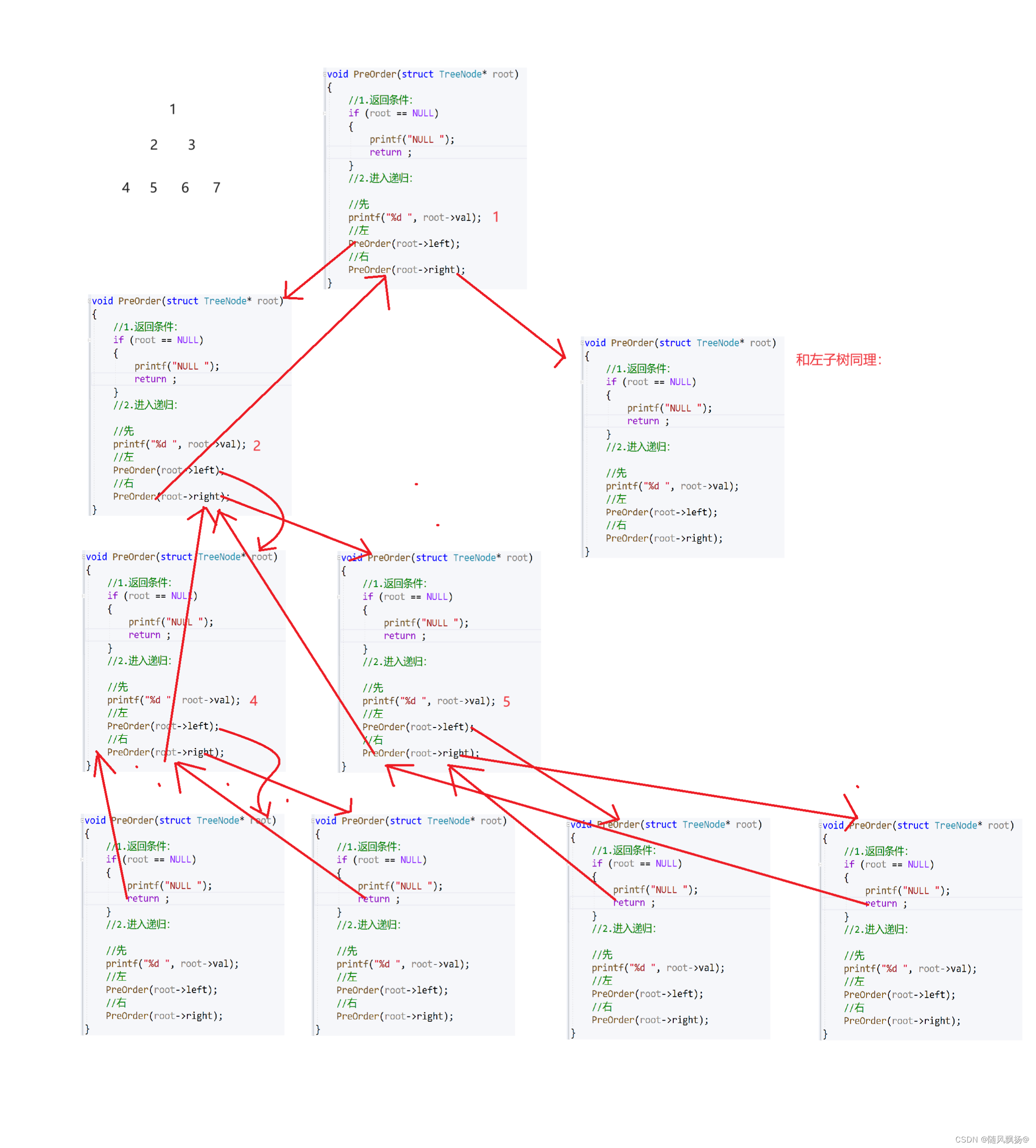
前序遍历:
//1.前序
void PreOrder(struct TreeNode* root)
{//1.返回条件:if (root == NULL){printf("NULL ");return ;}//2.进入递归://先printf("%d ", root->val);//左PreOrder(root->left);//右PreOrder(root->right);
}
中序遍历:
//2.中序
void InOrder(struct TreeNode* root)
{//1.返回条件:if (root == NULL){printf("NULL ");return;}//2.进入递归://左PreOrder(root->left);//根:printf("%d ", root->val);//右PreOrder(root->right);
}
后序遍历:
//3.后序
void PostOrder(struct TreeNode* root)
{//1.返回条件:if (root == NULL){printf("NULL ");return;}//2.进入递归://左PreOrder(root->left);//右PreOrder(root->right);//根:printf("%d ", root->val);
}
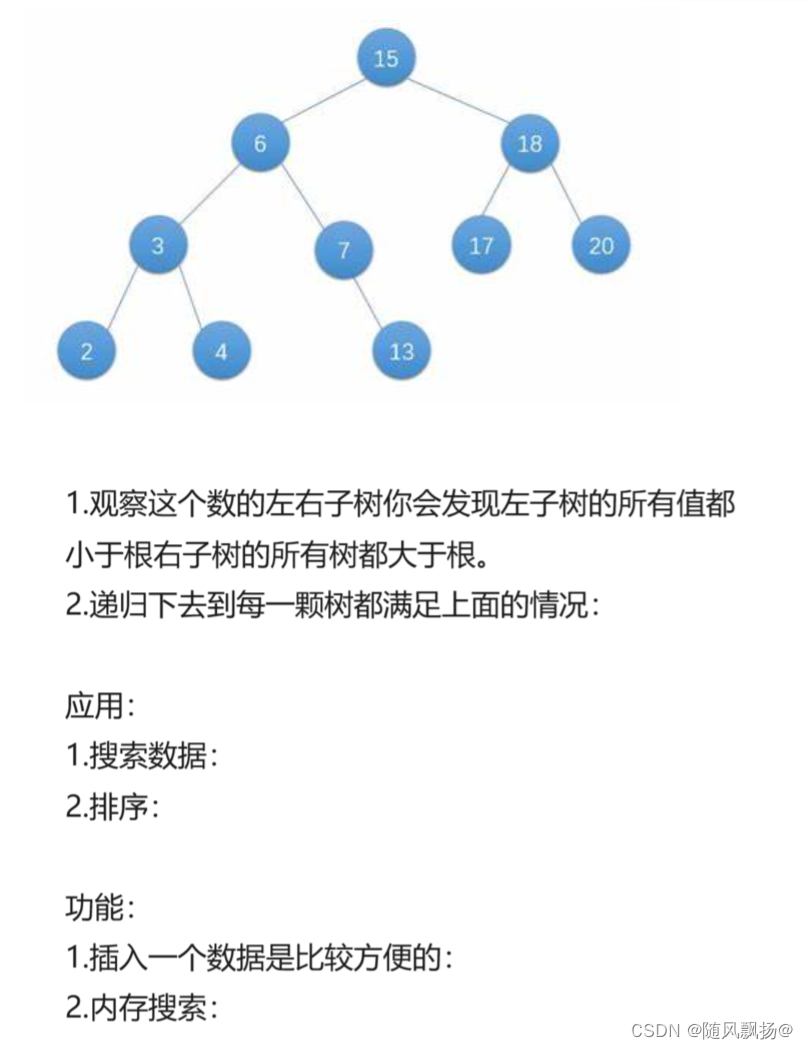
2.内容拓展:
一.普通二叉树:
1.增删查改是没有意义的:内容上的增删查改对二叉树的结构造成破坏:二.二叉搜索树(链式结构):
1.AVL树:
2.红黑树:
3.二叉树的oj题目:
二.二叉树链式(题目)
题目一:计算节点的个数:
方法一:注意事项:
1.创建在函数里面创建静态局部变量进入递归函数这个变量不会再一次创建:
2.注意root到空的时候的返回值为0:
3.注意不要去创建多个树如果存在多个树去计算节点会导致静态变量数值的问题:
//题目一:计算节点个数://方法一(使用局部静态):
int TreeSize(TN* root)
{//1.返回条件:if (root == NULL){return 0;}//只会在第一次进入函数去定义:static int num = 0;//2.进入递归://1.当前节点:num++;//2.左:TreeSize(root->left);//3.右:TreeSize(root->right);return num;
}
方法二:注意事项:
1.使用分治的思路去每次加上一个当前节点的个数。
2.当节点为空的时候就返回一个0.
3.注意:这个函数可以同时去计算多个树的节点个数:
//方法二(使用分治的思路):
int TreeSize2(TN* root)
{if (root == NULL)return 0;//左节点+右节点return TreeSize2(root->left) + TreeSize2(root->right) + 1;
}
题目二:计算叶子节点的个数:
方法一:
1,叶子节点是没有左子树没有右子树的就是叶子节点:
2.遍历每一个节点,并且判断节点是否是叶子节点:
3.使用分治的思路去计数:
int TreeLeafSize(TN* root)
{//1.只有叶子才返回:if (root->left == NULL && root->right==NULL){return 1;}//2.进入左右子树递归:return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}题目三:求第K层节点的个数:
方法一:
1.函数需要传参数K
2.找根节点的K层就相当于找根节点左子树根的第K-1层:
3.找根节点的K层就相当于找根节点右子树根的第K-1层:
4.进入函数不要多次的进行–,k–不要写在函数中:下一次进入右树的时候就不需要再一次的–了!
//题目三:计算第K层节点个数://方法一:int TreeKSize(TN* root, int k)
{assert(k!=0);//1.如果在k层没有到的情况下到空返回0if (root == NULL){return 0;}//2.当到达K层的时候。if (k == 1){return 1;}//3.没有到达K层并且没有为空的时候就进入递归://3-1:进入不同的栈中只要是同层的就可以保证K值相同:k--;return TreeKSize(root->left, k)+TreeKSize(root->right,k);
}
题目四:
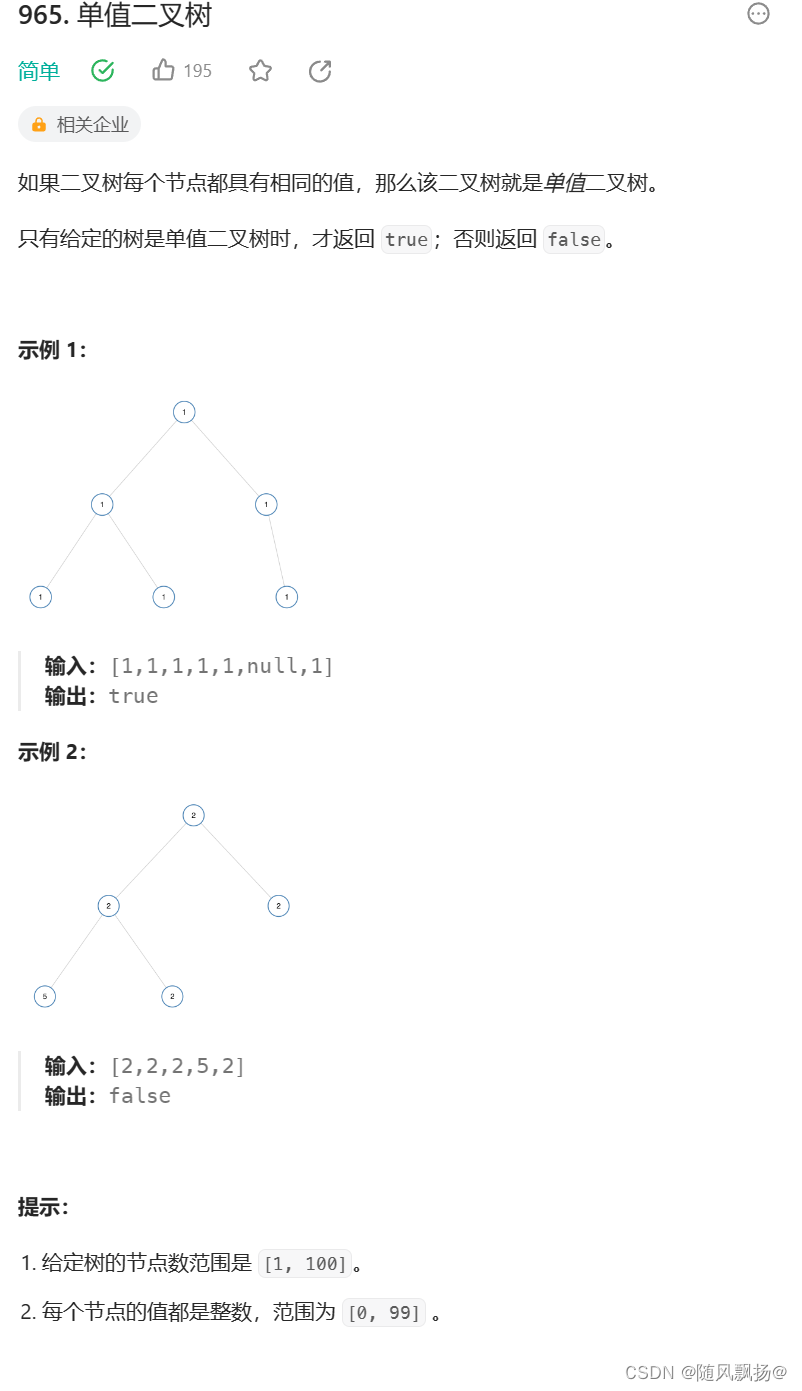
题目链接:单值二叉树
方法一:重新定义一个函数:
1.我们前面大部分的操作就是root为空就返回(true)(因为我们是比较数值是否相同所有返回true):
2…如果每一次通过root的数值去判断我们是需要传数值到递归的下一个部分:
3.如果左子树有不相等的就直接返回false(就不需要进入右子树判断):
4.如果左右相等的就继续函数不需要返回(继续进入函数)。
bool isUnivalTreeNode(struct TreeNode* root,int val)
{//1.到空树:if(root==NULL){return true;}//2.数值相同:if(root->val==val){}else if(root->val!=val){return false;}//左子树:if(isUnivalTreeNode(root->left,root->val)){//右子树:return isUnivalTreeNode(root->right,root->val);}return false;
}bool isUnivalTree(struct TreeNode* root){//左子树:if(isUnivalTreeNode(root->left,root->val)){//右子树:return isUnivalTreeNode(root->right,root->val);}return false;
}
方法二:(判断左右节点数值和root数值)
1.如果根为空就返回真:
2.如果左右子树的根节点数值和当前root的数值相同就继续递归进入。
3.如果左右子树中有一个节点数值和root的数值不相同就返回
bool isUnivalTree(struct TreeNode* root){if(root==NULL)return true;//1.这两个思路可以解决一个为空,一个有的情况。//2.解决两个都为空的情况。//3.解决两个都不是空的情况。if(root->left!=NULL && root->left->val != root->val){return false;}if(root->right!=NULL && root->right->val != root->val){return false;}//进入递归:return isUnivalTree(root->left) && isUnivalTree(root->right);
}
题目五:二叉树的最大深度:
方法一:
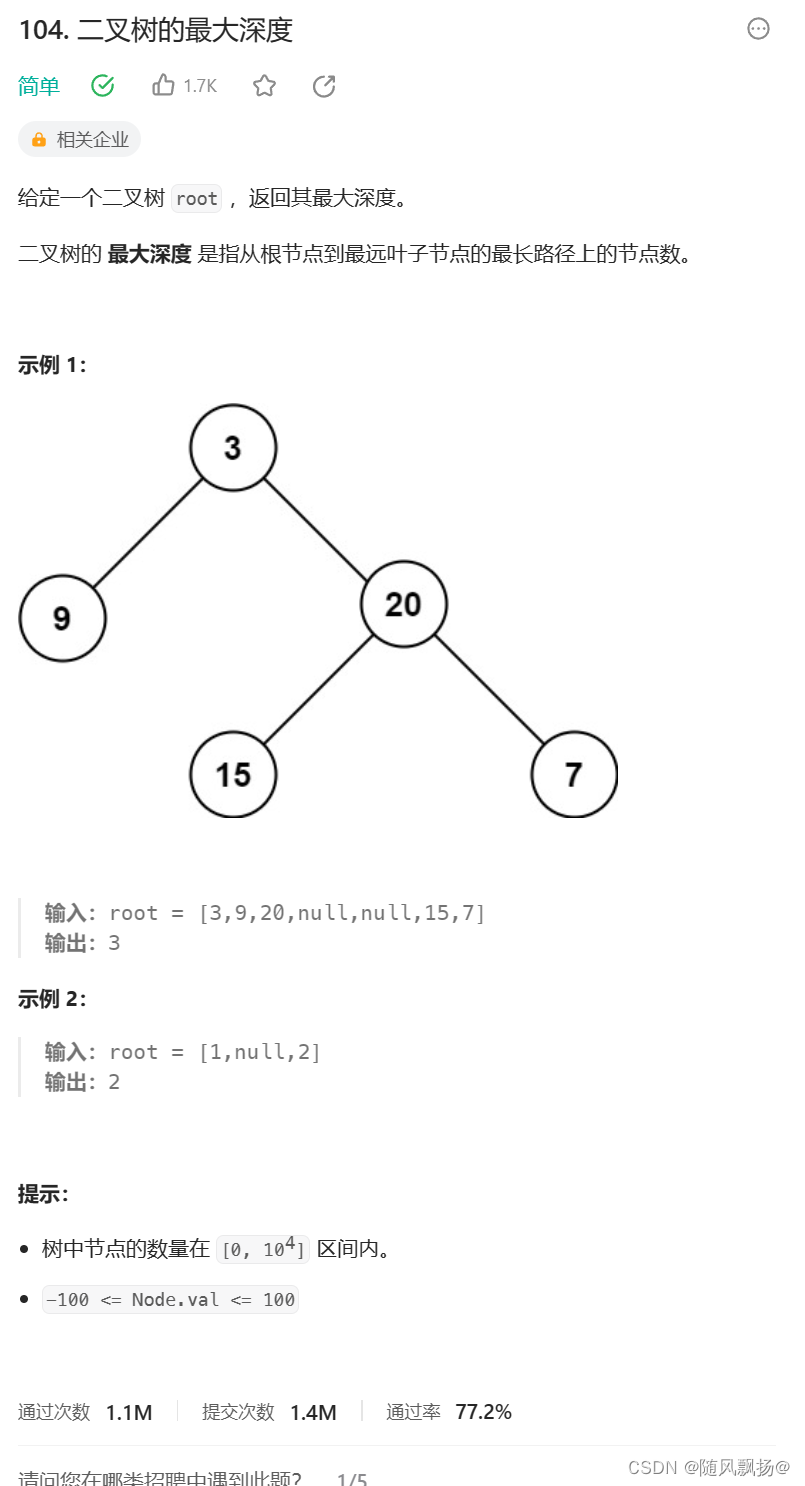
二叉树的深度
1.如果到空就返回0,空不是节点数。
2.每一次比较左右的数的值拿出较大的数值进行+1这个+1就相当加上当前节点。
3.子树的根节点不是空就继续。
int maxDepth(struct TreeNode* root){//1.左为空返回0(空节点不是节点数是一个返回的标志)。//2.右子树不是空就继续进入函数。if(root==NULL)return 0;//2.比较左右子树的返回值取较大的数值:int max=maxDepth(root->left);int max1=maxDepth(root->right); if(max1>max){max=max1;}//在回去的过程中自己也是节点return max+1;
}
相关文章:

数据结构基础7:二叉树【链式结构】实现和递归思想。
二叉树的链式结构实现 一.二叉树链式结构的实现:1.前置说明:1.创建二叉树:2.二叉树的结构: 2.二叉树的遍历:1.二叉树的前中后序遍历:2.内容拓展: 二.二叉树链式(题目)题目一:计算节点…...

[.NET 6] IHostedService 的呼叫等等我的爱——等待Web应用准备就绪
📢欢迎点赞 :👍 收藏 ⭐留言 📝 如有错误敬请指正,赐人玫瑰,手留余香!📢本文作者:由webmote 原创📢作者格言:新的征程,我们面对的不是技术而是人心,人心不可测,海水不可量,唯有技术,才是深沉黑夜中的一座闪烁的灯塔 !序言 在这篇文章中,我将介绍如何等…...

基于jeecg-boot的flowable流程自定义业务退回撤回或驳回到发起人后的再次流程提交
更多nbcio-boot功能请看演示系统 gitee源代码地址 后端代码: https://gitee.com/nbacheng/nbcio-boot 前端代码:https://gitee.com/nbacheng/nbcio-vue.git 在线演示(包括H5) : http://122.227.135.243:9888 主要…...

python如何学习
功能如此强大、高效的Python,却非常的简单好学,这让学它的同学爱不释手,也让越来越多的互联网企业开始用Python来做主要的开发语言,比如谷歌、Facebook(现Meta)、豆瓣、知乎等知名互联网公司都在使用Python…...

Centos7更新php7.2版本升级
之前搭建的LNMP环境php使用yum安装的版本为7.2,现有项目wordpress安装wp插件需要php7.4版本的支持,需要在原来的环境更新php版本。 一、卸载php7.2 yum remove php*原先的安装方式是yum安装直接yum remove就可以卸载否则需要rpm命令查询,按…...

操作系统学习笔记---计算机系统概述
目录 概念 功能和目标 特征 并发 共享(资源共享) 虚拟 异步 发展与分类 手工操作阶段(无OS) 批处理阶段 单道批处理系统 多道批处理系统 分时操作系统 实时操作系统 网络操作系统 分布式计算机系统 个人计算机操…...

uniapp H5 navigateBack无法返回上一层级
项目场景: 提交表单后需要返回上一级 原因分析: H5在PC端打开,当前页面重新加载的情况下,出现navigateBack不能返回,由于H5端页面刷新后返回页面栈会消失 //提交 const handleSubmit async () > {form.value?.a…...

Android性能优化之应用瘦身(APK瘦身)
关于作者:CSDN内容合伙人、技术专家, 从零开始做日活千万级APP。 专注于分享各领域原创系列文章 ,擅长java后端、移动开发、人工智能等,希望大家多多支持。 目录 一、导读二、概览2.1 apk组成 三、优化方向3.1 源代码3.1.1 代码混…...
C语言数组和指针笔试题(二)(一定要看)
目录 字符数组二例题1例题2例题3例题4例题5例题6例题7总结 字符数组三例题1例题2例题3例题4例题5例题6例题7 字符数组二 char arr[] {a,b,c,d,e,f} 1:printf("%d\n", strlen(arr)); 2:printf("%d\n", strlen(arr0)); 3:printf("%d\n", strlen(…...

uniapp——实现在线选座功能——技能提升
首先声明一点:下面的内容是从一个uniapp的程序中摘录的,并非本人所写,先做记录,以免后续遇到相似需求抓耳挠腮。 这里写目录标题 效果图代码——html部分cu-custom组件anil-seat组件 代码——jscss部分 效果图 代码——html部分 …...

领域驱动设计:微服务的各种边界
文章目录 演进式架构微服务还是小单体?微服务边界的作用 在用 DDD 进行微服务设计时,我们可以通过事件风暴来确定领域模型边界,划定微服务边界,定义业务和系统运行边界,从而保证微服务的单一职责和随需而变的架构演进能…...

MySQL之数据类型
目录 一、MySQL数据类型分类 二、数值类型 1、整数类型 2、bit类型 3、小数类型 三、字符串类型 1、char 2、varchar 3、char和varchar比较 四、日期和时间类型 五、enum和set 一、MySQL数据类型分类 MySQL 数据类型可以大致分为以下三类: 数值类型:用于…...

词法作用域改变词法作用域
一、词法作用域 1.定义: 为什么叫词法作用域?因为大部分标准语言编译器的第一个工作阶段叫作词法化,词法化的过程会对源代码中的字符进行检查,如果是有状态的解析过程,还会赋予单词语义。 简单来说࿰…...
,重载(overload),重写(override)小结。)
关于C++的隐藏 (hidden),重载(overload),重写(override)小结。
关于隐藏 (hidden) 假如继承以后,子类出现父类同名函数, 即使参数的形式不同, 也会导致父类的函数隐藏, 不参与函数匹配,不能使用。 这个链接讲的不错。https://zhuanlan.zhihu.com/p/575423511 #include <iostrea…...

算法通关村18关 | 透析回溯的模板
回溯有清晰的解题模板, void backtracking(参数){if (终止条件){存放结果;return;}for (选择本层中的集合元素(画成树,就是树节点孩子的大小) {处理节点;backtracking();回溯,撤销处理结果;}} 1. 从N叉树说起 在回溯之前&#x…...
)
【论文阅读】Untargeted Backdoor Attack Against Object Detection(针对目标检测的无目标后门攻击)
文章目录 一.论文信息二.论文内容0.摘要1.论文概述2.背景介绍3.作者贡献4.重点图表 一.论文信息 论文题目: Untargeted Backdoor Attack Against Object Detection(针对目标检测的无目标后门攻击) 发表年份: 2023-ICASSP&#x…...
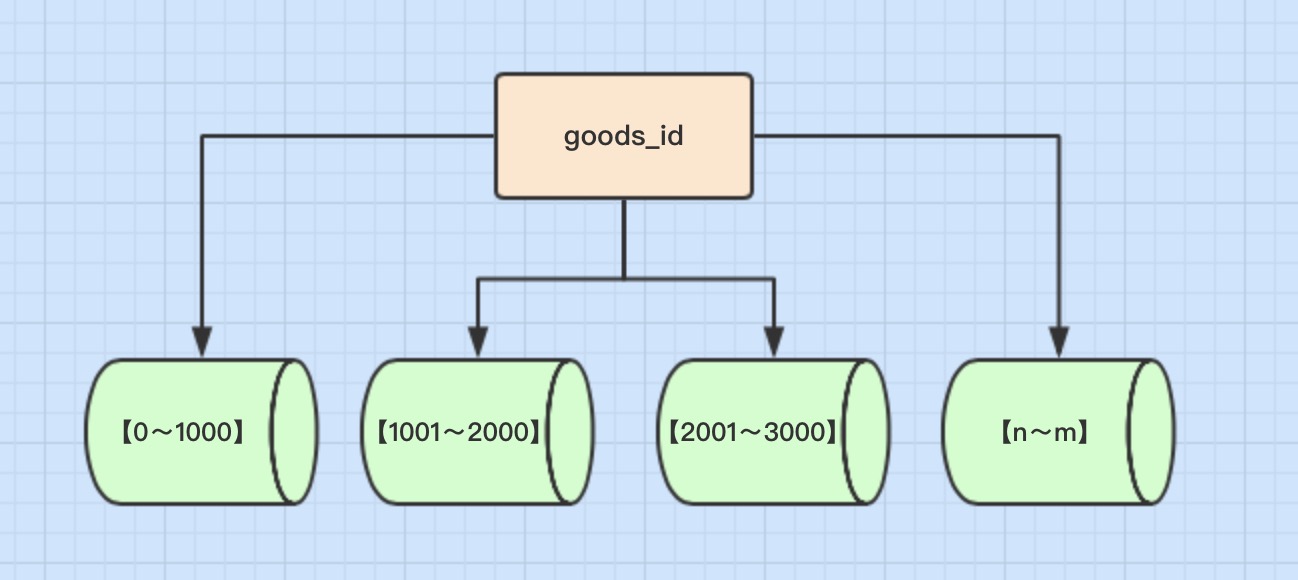
分库分表---理论
目录 一、垂直切分 1、垂直分库 2、垂直分表 3、垂直切分优缺点 二、水平切分 1、水平分库 2、水平分表 3、水平切分优缺点 三、数据分片规则 1、Hash取模分表 2、数值Range分表 3、一致性Hash算法 四、分库分表带来的问题 1、分布式事务问题 2、跨节点关联查询…...

[golang 流媒体在线直播系统] 2.搭建基于golang的流媒体服务器实现拉流推流,以及Html客户端拉取hls类型的流
一.使用 Go 语言的开源框架Livego搭建流媒体服务器 1.Livego 框架的介绍 Go 语言拥有强大的 服务器性能 ,golang 在语言级别解决了 多进程并发 的问题,支持 多核 CPU均衡使用 ,支持 海量轻量级线程 ,所以非常适合做 流媒体服务器 .而 livego 是基于golang 开发的简单高效的…...

9月12日作业
作业代码 #include <iostream>using namespace std;class Shape { protected:double cir;double area; public://无参构造Shape() {cout<<"无参构造"<<endl;}//有参构造Shape(double c, double a):cir(c), area(a){cout<<"有参构造&quo…...
React框架下如何集成H.265网页流媒体视频播放器EasyPlayer.js?
H5无插件流媒体播放器EasyPlayer属于一款高效、精炼、稳定且免费的流媒体播放器,可支持多种流媒体协议播放,可支持H.264与H.265编码格式,性能稳定、播放流畅,能支持WebSocket-FLV、HTTP-FLV,HLS(m3u8&#…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...