熵 | 无线通信知识
文章目录
- 一、信息论(熵、联合熵、条件熵)
- 二、Bernoulli熵
- 三、联合熵和条件熵
- 四、互信息
- 五、相对熵(KL距离)
- 六、微分熵
- 七、最大熵分布
- 常需要的不等式公式
一、信息论(熵、联合熵、条件熵)
熵定义: H ( X ) = E [ − l o g 2 p ( x ) ] = − ∑ x ∈ X p ( x ) l o g 2 p ( x ) H(X)=E[-log_2p(x)]=-\sum_{x\in X}p(x)log_2p(x) H(X)=E[−log2p(x)]=−x∈X∑p(x)log2p(x)
note
- H(X)是X的平均香农信息内容
- H(X)是每个符号的平均信息量
- 二元问题(抛硬币),H(X)取值为[H(X),H(X)+1]
为什么用 l o g 2 ( . ) log_2(.) log2(.)衡量信息
非负性: f ( p ) ≥ 0 f(p)\ge0 f(p)≥0, 0 ≤ p ≤ 1 0\le p\le1 0≤p≤1
特殊点:当p=0, f ( p ) = ∞ f(p)=\infty f(p)=∞
可加性
单调递增连续性 ??
二、Bernoulli熵
符号集 χ = [ 0 , 1 ] \chi=[0,1] χ=[0,1],对应的概率 p ⃗ = [ p , 1 − p ] \vec{p}=[p,1-p] p=[p,1−p]
Bernoulli熵: H ( X ) = H ( p ) = − p l o g 2 p − ( 1 − p ) l o g 2 ( 1 − p ) H(X)=H(p)=-plog_2p-(1-p)log_2(1-p) H(X)=H(p)=−plog2p−(1−p)log2(1−p)
note:
- 通常用 H ( p ) H(p) H(p)表示 H ( X ) H(X) H(X)
- p=0 or 1时, H ( p ) = 0 H(p)=0 H(p)=0
- H ( p ) H(p) H(p)是p的凸函数
- p=0.5, H ( p ) H(p) H(p)最大
- H ( p ) H(p) H(p)的取值范围 0 ≤ H ( p ) ≤ l o g 2 ∣ χ ∣ 0\le H(p)\le log_2|\chi| 0≤H(p)≤log2∣χ∣

三、联合熵和条件熵
联合熵:
H ( X , Y ) = − E l o g p ( x , y ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) l o g p ( x , y ) H(X,Y)=-Elogp(x,y)=-\sum_{x\in X} \sum_{y\in Y} p(x,y)logp(x,y) H(X,Y)=−Elogp(x,y)=−x∈X∑y∈Y∑p(x,y)logp(x,y)
条件熵
H ( Y ∣ X ) = − E l o g ( y ∣ x ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) l o g p ( y ∣ x ) H(Y|X)=-Elog(y|x)=-\sum_{x\in X} \sum_{y\in Y}p(x,y)logp(y|x) H(Y∣X)=−Elog(y∣x)=−x∈X∑y∈Y∑p(x,y)logp(y∣x)
H ( Y ∣ X ) = ∑ x ∈ X p ( x ) H ( Y ∣ X = x ) H(Y|X)=\sum_{x\in X}p(x)H(Y|X=x) H(Y∣X)=x∈X∑p(x)H(Y∣X=x)
熵的链式法则
- H ( X , Y ) = H ( X ) + H ( Y ∣ X ) H(X,Y)=H(X)+H(Y|X) H(X,Y)=H(X)+H(Y∣X)
- H ( X , Y ∣ Z ) = H ( X ∣ Z ) + H ( Y ∣ X , Z ) H(X,Y|Z)=H(X|Z)+H(Y|X,Z) H(X,Y∣Z)=H(X∣Z)+H(Y∣X,Z)
- H ( X 1 , X 2 , . . . . X n ) = ∑ i = 1 n H ( X i ∣ X i − 1 , . . . . X 1 ) H(X_1,X_2,....X_n)=\sum_{i=1}^{n}H(X_i|X_{i-1},....X_1) H(X1,X2,....Xn)=∑i=1nH(Xi∣Xi−1,....X1)
四、互信息
定义:
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X;Y)=H(X)-H(X|Y)=H(X)+H(Y)-H(X,Y) I(X;Y)=H(X)−H(X∣Y)=H(X)+H(Y)−H(X,Y)
互信息具有对称性
I ( X ; Y ) = H ( X ) − H ( X ∣ Y ) = H ( Y ) − H ( Y ∣ X ) I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X) I(X;Y)=H(X)−H(X∣Y)=H(Y)−H(Y∣X)
I ( X ; Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I(X;Y)=H(X)+H(Y)-H(X,Y) I(X;Y)=H(X)+H(Y)−H(X,Y)
I ( X ; Y ) = I ( Y , X ) I(X;Y)=I(Y,X) I(X;Y)=I(Y,X)
I ( X ; X ) = H ( X ) I(X;X)=H(X) I(X;X)=H(X)
I ( X ; Y ) ≥ 0 I(X;Y)\ge0 I(X;Y)≥0,当且仅当X Y互相独立时,等号成立
互信息的链式法则
I ( X 1 , X 2 , . . . . X n ; Y ) = ∑ i = 1 n I ( X i ; Y ∣ X i − 1 , . . . . , X 1 ) I(X_1,X_2,....X_n;Y)=\sum_{i=1}^nI(X_i;Y|X_{i-1},....,X_1) I(X1,X2,....Xn;Y)=i=1∑nI(Xi;Y∣Xi−1,....,X1)
五、相对熵(KL距离)
D ( p ⃗ ∣ ∣ q ⃗ ) = ∑ x ∈ X p ( x ) l o g q ( x ) p ( x ) = E p ⃗ [ − l o g q ( x ) ] − H ( p ⃗ ) D(\vec{p}||\vec{q})=\sum_{x\in X}p(x)log\frac{q(x)}{p(x)}=E_{\vec{p}}[-logq(x)]-H(\vec{p}) D(p∣∣q)=x∈X∑p(x)logp(x)q(x)=Ep[−logq(x)]−H(p)
D ( p ⃗ ∣ ∣ q ⃗ ) D(\vec{p}||\vec{q}) D(p∣∣q)测量的是两个概率分布 p ⃗ \vec{p} p和 q ⃗ \vec{q} q间的距离,并非真实距离
D ( p ⃗ ∣ ∣ q ⃗ ) ≥ 0 D(\vec{p}||\vec{q})\ge 0 D(p∣∣q)≥0,当且仅当 p ⃗ \vec{p} p= q ⃗ \vec{q} q,等号成立
六、微分熵
对于连续型随机变量,一个以f(x)为密度函数的连续型随机变量,X的微分熵h(x)为:
h ( x ) = ∫ − ∞ ∞ f X ( x ) l o g f X ( x ) d x = E − l o g f X ( x ) h(x)=\int_{-\infty}^{\infty}f_X{(x)}logf_X(x)dx=E-logf_X(x) h(x)=∫−∞∞fX(x)logfX(x)dx=E−logfX(x)
note
- 微分熵仅依赖于随机变量的概率密度函数,有时候将微分熵写为h(f)
- 微分熵可以为负值
微分熵分类
| 均匀分布的微分熵 | 高斯分布的微分熵 | 多元高斯分布的微分熵 | |
|---|---|---|---|
| 前提条件:随机变量服从 | 均匀分布 X ∼ U ( a , b ) X\sim U(a,b) X∼U(a,b) | 高斯分布 X ∼ U ( μ , σ 2 ) X\sim U(\mu,\sigma^2) X∼U(μ,σ2) | X 1 : n ∼ N ( m ⃗ , k ⃗ ) X_{1:n}\sim N(\vec{m},\vec{k}) X1:n∼N(m,k) |
| f ( x ) = { 1 b − a , x ∈ ( a , b ) ) 0 e l s e f(x)=\left\{\begin{matrix}\frac{1}{b-a} ,&x\in(a,b)) \\ 0 &else \end{matrix}\right. f(x)={b−a1,0x∈(a,b))else | f ( x ) = 1 ( 2 π σ 2 ) 1 2 e x p { − 1 2 σ 2 ( x − μ ) 2 } f(x)=\frac{1}{(2\pi\sigma^2)^{\frac{1}{2}}}exp\{-\frac{1}{2\sigma^2}(x-\mu)^2\} f(x)=(2πσ2)211exp{−2σ21(x−μ)2} | f ( x ) = ∣ 2 π k ⃗ ∣ 1 2 e x p { − 1 2 ( x − m ⃗ ) T k ⃗ − 1 ( x − m ⃗ ) } f(x)=|2\pi\vec{k}|^\frac{1}{2}exp\{-\frac{1}{2}(x-\vec{m})^T\vec k^{-1}(x-\vec m)\} f(x)=∣2πk∣21exp{−21(x−m)Tk−1(x−m)}m:均值矢量 k ⃗ \vec k k协方差矢量 | |
| 微分熵 | h ( x ) = ∫ a b f ( x ) l o g f ( x ) d x = l o g ( b − a ) h(x)=\int_a^bf(x)logf(x)dx=log(b-a) h(x)=∫abf(x)logf(x)dx=log(b−a)当b-a<1时,h(x)<0 | h ( x ) = − l o g e ∫ − ∞ ∞ f ( x ) l n f ( x ) d x = 1 2 l o g ( 2 π e σ 2 ) h(x)=-loge\int_{-\infty}^{\infty}f(x)lnf(x)dx=\frac{1}{2}log(2\pi e\sigma^2) h(x)=−loge∫−∞∞f(x)lnf(x)dx=21log(2πeσ2) | h ( x ) = 1 2 l o g ∣ 2 π e k ⃗ ∣ h(x)=\frac{1}{2}log|2\pi e\vec k| h(x)=21log∣2πek∣ |
七、最大熵分布
-
条件一:(幅值约束)对于r有限长范围(a,b)使其最大熵的分布是均匀分布
u ( x ) = 1 b − a → u(x)=\frac{1}{b-a} \rightarrow u(x)=b−a1→、 0 ≤ D ( f ∣ ∣ x ) → h f ( x ) = l o g ( b − a ) 0 \le D(f||x) \rightarrow h_f(x)=log(b-a) 0≤D(f∣∣x)→hf(x)=log(b−a) -
条件二:(功率约束)给定协方差矩阵 k ⃗ \vec k k,零均值的多元高斯分布能使熵在 ( − ∞ , ∞ ) n (-\infty,\infty)^n (−∞,∞)n上最大
ϕ ( x ) = ∥ 2 π k ⃗ ∥ 1 2 e x p { − 1 2 x T k ⃗ − 1 x ⃗ } \phi (x)=\|2\pi\vec{k}\|^\frac{1}{2}exp\{-\frac{1}{2}x^T\vec k^{-1}\vec x\} ϕ(x)=∥2πk∥21exp{−21xTk−1x};
0 ≤ D ( f ∣ ∣ x ) = h f ( x ) − E f l o g ϕ ( x ) → h f ( x ) ≤ − ( l o g e ) E f ( − 1 2 l n ∣ 2 π k ⃗ ∣ − 1 2 x T k ⃗ − 1 x ) = h ϕ ( x ) 0 \le D(f||x)=h_f(x)-E_flog\phi(x) \rightarrow h_f(x)\le-(loge)E_f(-\frac{1}{2}ln|2\pi \vec k|-\frac{1}{2}x^T \vec k^{-1}x)=h_{\phi (x)} 0≤D(f∣∣x)=hf(x)−Eflogϕ(x)→hf(x)≤−(loge)Ef(−21ln∣2πk∣−21xTk−1x)=hϕ(x)
常需要的不等式公式
H ( Y ∣ X ) ≤ H ( X ) H(Y|X)\le H(X) H(Y∣X)≤H(X),X和Y互相独立时,等号成立
H ( X 1 , X 2 , . . . . X n ) ≤ ∑ i = 1 n H ( X i ) H(X_1,X_2,....X_n)\le \sum_{i=1}^nH(X_i) H(X1,X2,....Xn)≤∑i=1nH(Xi),当且仅当 X i X_i Xi互相独立时等号成立
参考文章:通信算法基础知识汇总(5)、通信算法基础知识汇总(8)
相关文章:

熵 | 无线通信知识
文章目录 一、信息论(熵、联合熵、条件熵)二、Bernoulli熵三、联合熵和条件熵四、互信息五、相对熵(KL距离)六、微分熵七、最大熵分布常需要的不等式公式 一、信息论(熵、联合熵、条件熵) 熵定义: H ( X ) E [ − l …...
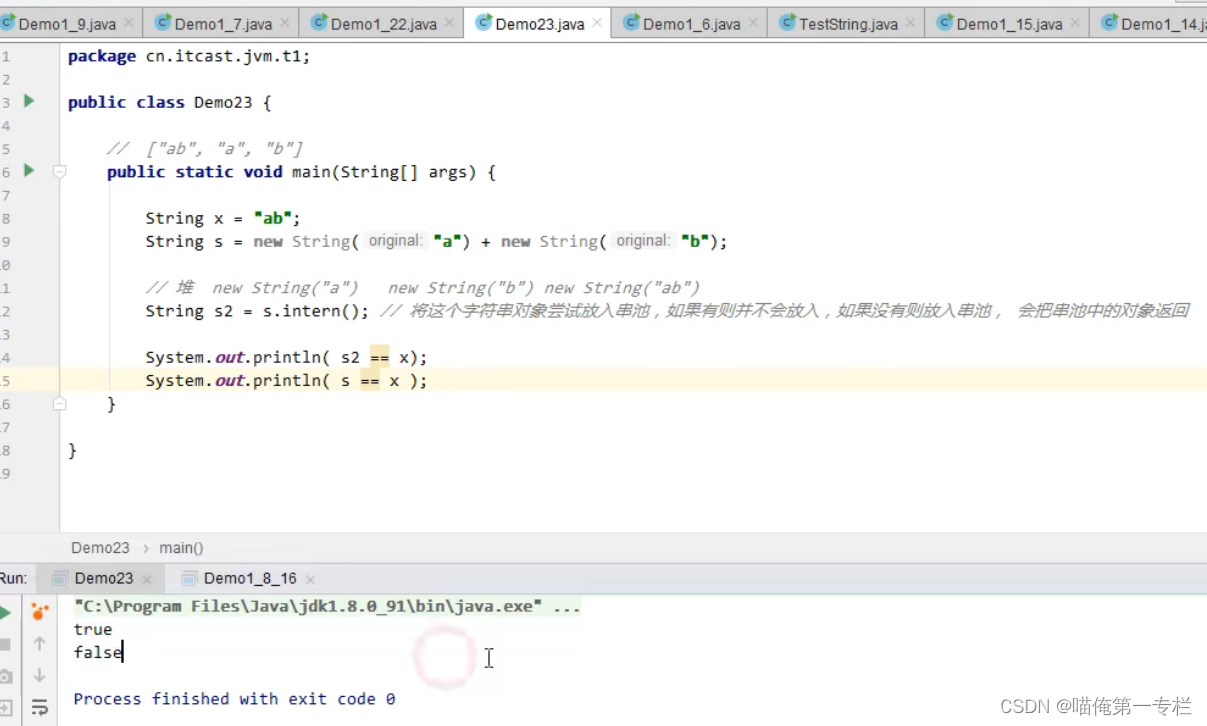
黑马JVM总结(七)
(1)StringTable_编译器优化 “a”“b”对应#4:是去常量池中找ab的这个符号 astore 5:是把这个存入编号为5的局部变量 “ab”对应的指令 #4,跟“a”“b”对应#4下面弄是一样的 在执行s3“ab”这行个代码时…...

Vue3核心语法一
Vue3核心语法一 rectiveshallowReactiverefcomputedwatchwatchEffet 使用Vue3创建项目template中标签可以多个根标签,可以通过setup开启组合式API,组合式API优点可以使相同业务放到一起 rective 定义响应式数据, import { reactive} from "vue";const data reactiv…...

5.11.Webrtc接口的设计原理
在上节课中呢,我向你介绍了web rtc的接口宏,那有很多同学会产生疑问啊,那觉得web rtc为什么要把接口设计的这么复杂?还非要通过宏来实现一个代理类,再通过代理类来调用到web rtc内部。 那为什么要这么设计呢…...

2022年09月 C/C++(八级)真题解析#中国电子学会#全国青少年软件编程等级考试
C/C++编程(1~8级)全部真题・点这里 第1题:道路 N个以 1 … N 标号的城市通过单向的道路相连:。每条道路包含两个参数:道路的长度和需要为该路付的通行费(以金币的数目来表示) Bob and Alice 过去住在城市 1.在注意到Alice在他们过去喜欢玩的纸牌游戏中作弊后,Bob和她分手…...
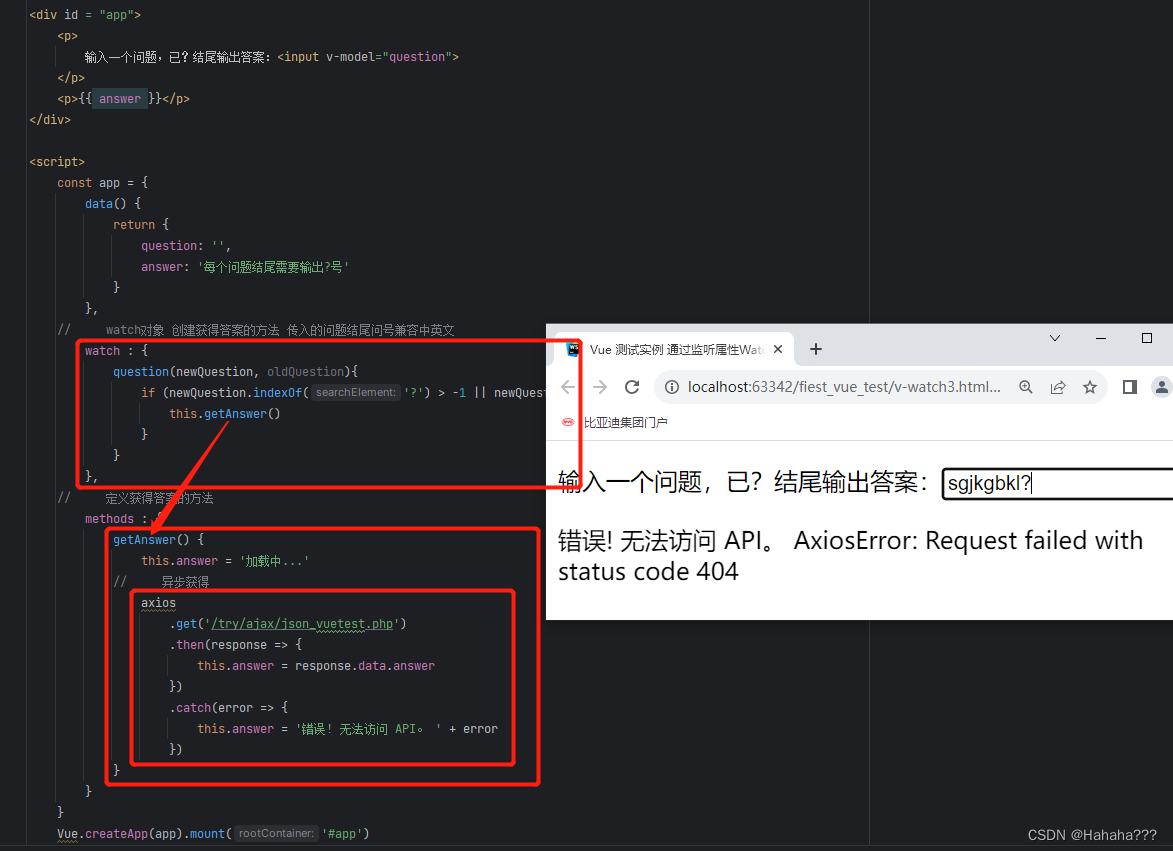
Vue3 监听属性-watch
文章目录 Vue3 监听属性-watch1. 概念2. 实例2.1 通过使用 watch 实现计数器2.2 千米与米之间的换算2.3 异步加载中使用 watch2.4 小计 Vue3 监听属性-watch 1. 概念 Vue3 监听属性 watch,可以通过 watch 来响应数据的变化。 watch 的作用:用于监测响应…...
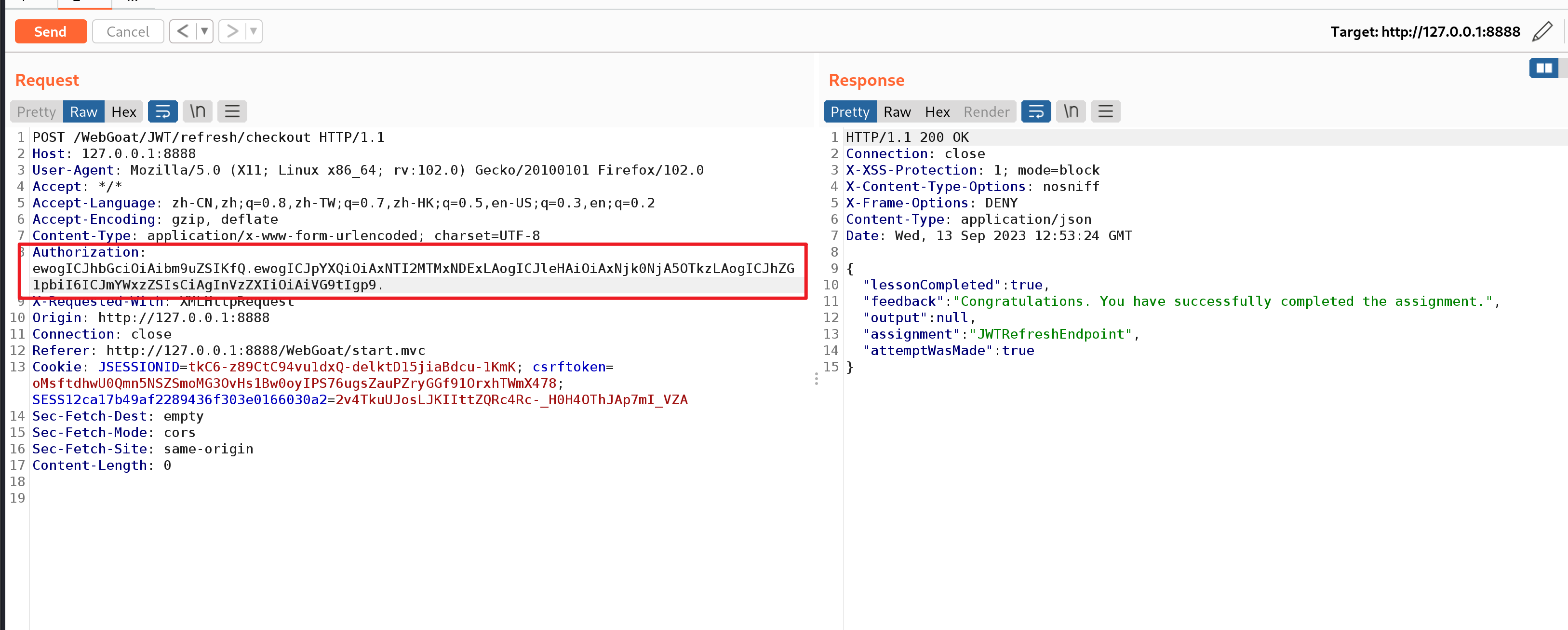
JWT安全
文章目录 理论知识cookie(放在浏览器)session(放在 服务器)tokenjwt(json web token)headerpayloadSignatureJWT通信流程 JWT与Token 区别相同点区别 WebGoat靶场--JWT tokens环境启动第四关第五关第七关 属于越权漏洞 理论知识 cookie(放在浏览器) …...
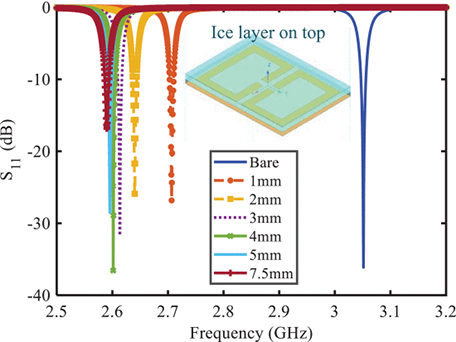
LabVIEW利用人工神经网络辅助进行结冰检测
LabVIEW利用人工神经网络辅助进行结冰检测 结冰对各个领域构成重大威胁,包括但不限于航空航天和风力涡轮机行业。在起飞过程中,飞机机翼上轻微积冰会导致升力降低25%。研究报告称,涡轮叶片上的冰堆积可在19个月的运行时间内造成29MWh的功率损…...

Linux安装MySQL8.0
又又又又..Linux装MySQL。 删除原有的MySQL 查看安装的mysql信息:rpm -qa|grep -i mysql 删除mysql相关服务:rpm -e --nodeps 查询mysql遗留文件和依赖信息:find / -name mysql 手动删除mysql配置文件:rm -rf /etc/my.cnf 相关…...
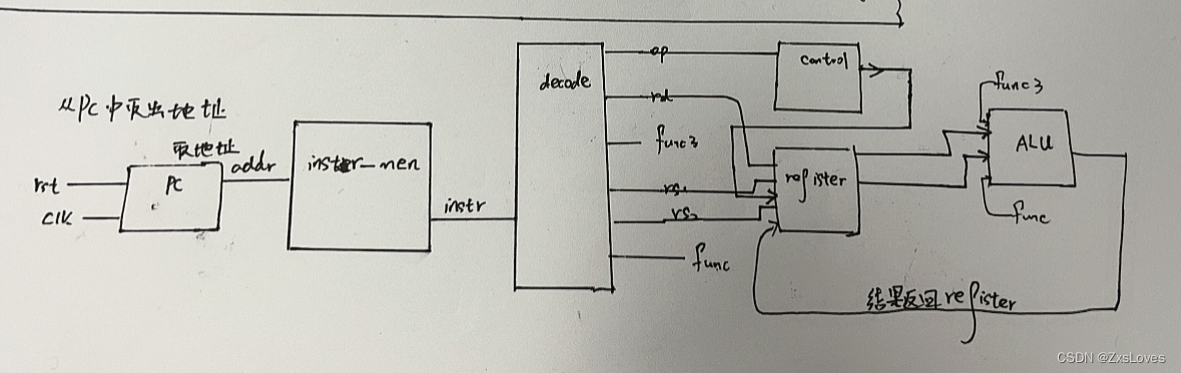
【【萌新编写RISCV之前言CPU的部分介绍.3】】
萌新编写RISCV之前言CPU的部分介绍.3 CPU的数字电路结构实际十分简单,最主要的模块有PC(地址生成),ALU(运算),Register(寄存),Decode(译码&#…...

dl_model_param
set_dl_model_param —设置深度学习模型的参数 get_dl_model_param — Return the parameters of a deep learning model 返回深度学习模型的参数 使用read_dl_model读取前一步初始化后的网络模型,得到模型的句柄DLModelHandle。 接着用read_dict读取预处理后的数…...
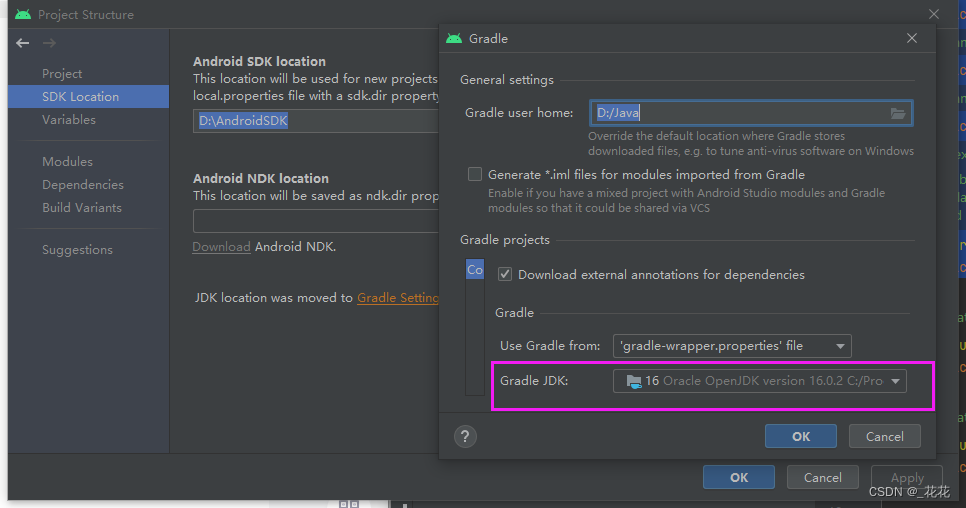
Android相机调用-CameraX【外接摄像头】【USB摄像头】
Android相机调用有原生的Camera和Camera2,我觉得调用代码都太复杂了,CameraX调用代码简洁很多。 说明文档:https://developer.android.com/jetpack/androidx/releases/camera?hlzh-cn 现有查到的调用资料都不够新,对于外接摄像…...

第一个Java程序
1. 将扩展名.text更改为.java 2.文件夹(Hello.java)上方输入“cmd空格回车”(没有加号) 3.在命令提示符内输入“javac空格文件夹名称.java回车” (javac空格Hello.java回车) 执行成功后,文件夹下多一个Hello.class…...

OpenCV之霍夫变换检测直线
霍夫变换 首先是笛卡尔坐标系到霍夫空间的转换,比如笛卡尔坐标系中有一条直线 yaxb。 笛卡尔坐标系中一条直线,对应霍夫空间的一个点。 反过来同样成立(霍夫空间的一条直线,对应笛卡尔坐标系的一个点) 原理其实很简单 …...
lv3 嵌入式开发-11 Linux下GDB调试工具
目录 1 GDB简介 2 GDB基本命令 3 GDB调试程序 1 GDB简介 GDB是GNU开源组织发布的一个强大的Linux下的程序调试工具。 一般来说,GDB主要帮助你完成下面四个方面的功能: 1、启动你的程序,可以按照你的自定义的要求随心所欲的运行程序&#…...
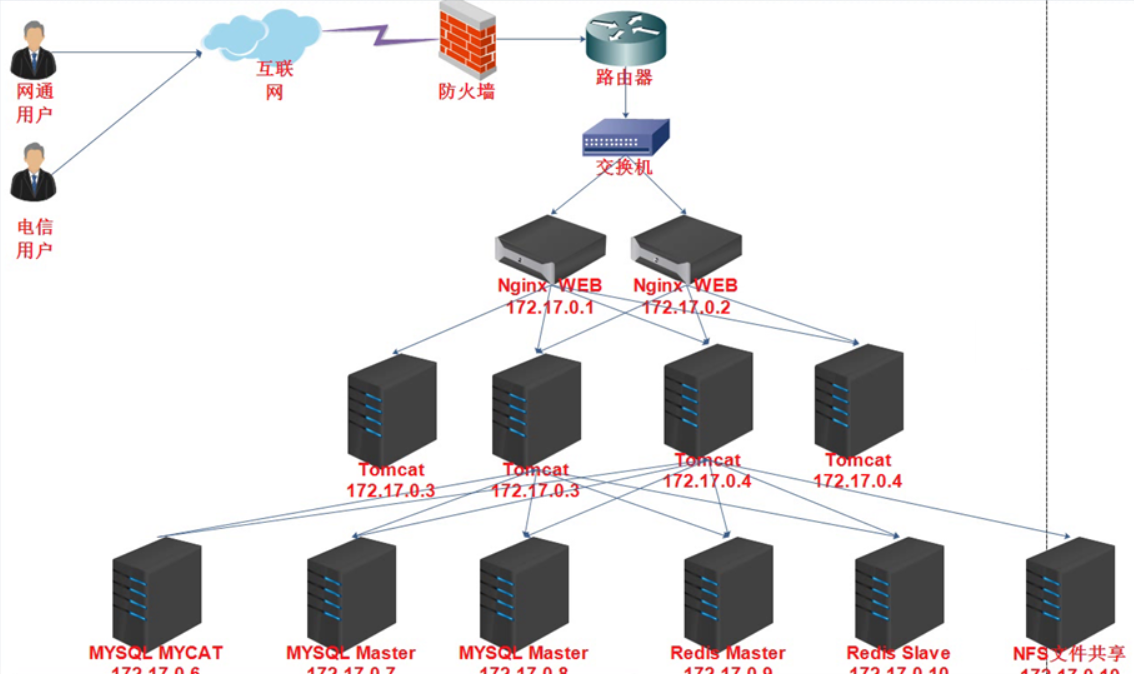
Zabbix监控平台概念
1.概念 Zabbix是一款开源的、免费的、分布式监控平台支持web管理,WEB界面可以方便管理员使用可以监控硬件服务器CPU温度、风扇转速、操作系统CPU、EME、DISK、I/O、流量宽带、负载、端口、进程等Zabbix是C/S架构,Client客户端和Server端组成 2.Zabbix可…...
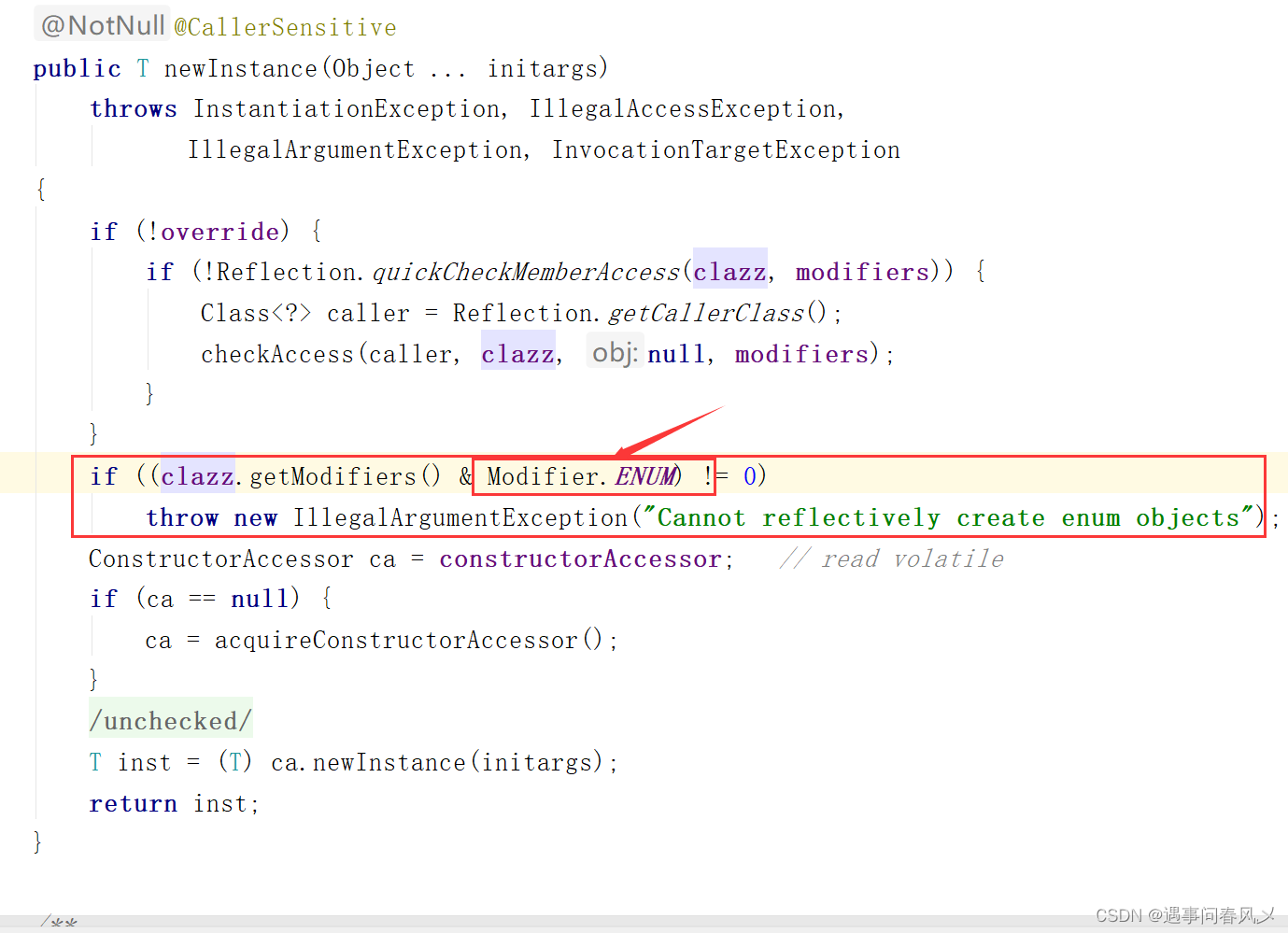
【javaSE】 枚举与枚举的使用
文章目录 🎄枚举的背景及定义⚾枚举特性总结: 🌲枚举的使用🚩switch语句🚩常用方法📌示例一📌示例二 🎍枚举优点缺点🌴枚举和反射🚩枚举是否可以通过反射&…...
NetSuite知识会汇编-管理员篇顾问篇2023
本月初,开学之际,我们发布了《NetSuite知识会汇编-用户篇 2023》,这次发布《NetSuite知识会汇编-管理员篇&顾问篇2023》。本篇挑选了近两年NetSuite知识会中的一些文章,涉及开发、权限、系统管理等较深的内容,共19…...

根号分治与多项式的巧妙结合:GYM-104386G
使用范围:序列上对于每种数的计数问题 考虑对每种数的出现次数进行根号分治 如果出现次数很少,直接平方暴力即可 如果很大考虑任意 ( i , j ) (i,j) (i,j),我们拆一下,再移一下,然后就变成了卷积形式...

通过FTP高速下载几百G数据
基因组下载 (FTP) 常见问题解答 基因组FTP站点有哪些亮点?下载多个基因组组装数据的最简单方法是什么?下载大型数据集的最佳协议是什么?为什么 NCBI 基因组 FTP 站点要重组?我如何及时了解 NCBI 基因组 FTP 站点的变化?...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Ubuntu Cursor升级成v1.0
0. 当前版本低 使用当前 Cursor v0.50时 GitHub Copilot Chat 打不开,快捷键也不好用,当看到 Cursor 升级后,还是蛮高兴的 1. 下载 Cursor 下载地址:https://www.cursor.com/cn/downloads 点击下载 Linux (x64) ,…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
Android屏幕刷新率与FPS(Frames Per Second) 120hz
Android屏幕刷新率与FPS(Frames Per Second) 120hz 屏幕刷新率是屏幕每秒钟刷新显示内容的次数,单位是赫兹(Hz)。 60Hz 屏幕:每秒刷新 60 次,每次刷新间隔约 16.67ms 90Hz 屏幕:每秒刷新 90 次,…...
