线性代数的本质(十)——矩阵分解
文章目录
- 矩阵分解
- LU分解
- QR分解
- 特征值分解
- 奇异值分解
- 奇异值分解
- 矩阵的基本子空间
- 奇异值分解的性质
- 矩阵的外积展开式
矩阵分解
矩阵的因式分解是把矩阵表示为多个矩阵的乘积,这种结构更便于理解和计算。
LU分解
设 A A A 是 m × n m\times n m×n 矩阵,若 A A A 可以写成乘积
A = L U A=LU A=LU
其中, L L L 为 m m m 阶下三角方阵,主对角线元素全是1。 U U U 为 A A A 得到一个行阶梯形矩阵。这样一个分解称为LU分解。 L L L 称为单位下三角方阵。
我们先来看看,LU分解的一个应用。当 A = L U A=LU A=LU 时,方程 A x = b A\mathbf x=\mathbf b Ax=b 可写成 L ( U x ) = b L(U\mathbf x)=\mathbf b L(Ux)=b,于是分解为下面两个方程
L y = b U x = y L\mathbf y=\mathbf b \\ U\mathbf x=\mathbf y Ly=bUx=y
因为 L L L 和 U U U 都是三角矩阵,每个方程都比较容易解。
LU 分解算法:本节只讲述仅用行倍加变换求解。可以证明,单位下三角矩阵的乘积和逆也是单位下三角矩阵 。此时,可以用行倍加变换寻找 L L L 和 U U U 。假设存在单位下三角初等矩阵 P 1 , ⋯ , P s P_1,\cdots,P_s P1,⋯,Ps 使
P 1 ⋯ P s A = U P_1\cdots P_sA=U P1⋯PsA=U
于是便得到了 U U U 和 L L L
L = ( P 1 , ⋯ , P s ) − 1 L=(P_1,\cdots,P_s)^{-1} L=(P1,⋯,Ps)−1
QR分解
如果 m × n m\times n m×n 矩阵 A A A 的列向量线性无关,那么 A A A 可以分解为 A = Q R A=QR A=QR,其中 Q Q Q 是一个 m × n m\times n m×n 正交矩阵,其列为 col A \text{col }A col A 的一组标准正交基, R R R 是一个上 n × n n\times n n×n 三角可逆矩阵,且其对角线上的元素全为正数。
证:矩阵 A = ( x 1 , x 2 , ⋯ , x n ) A=(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n) A=(x1,x2,⋯,xn) 的列向量是 col A \text{col }A col A 的一组基,使用施密特正交化方法可以构造一组标准正交基 u 1 , u 2 , ⋯ , u n \mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n u1,u2,⋯,un ,取
Q = ( u 1 , u 2 , ⋯ , u n ) Q=(\mathbf u_1,\mathbf u_2,\cdots,\mathbf u_n) Q=(u1,u2,⋯,un)
因为在正交化过程中 x k ∈ span { x 1 , ⋯ , x k } = span { u 1 , ⋯ , u k } , k = 1 , 2 , ⋯ , n \mathbf x_k\in\text{span}\{\mathbf x_1,\cdots,\mathbf x_k\}=\text{span}\{\mathbf u_1,\cdots,\mathbf u_k\},\quad k=1,2,\cdots,n xk∈span{x1,⋯,xk}=span{u1,⋯,uk},k=1,2,⋯,n 。所以 x k \mathbf x_k xk 可线性表示为
x k = r 1 k u 1 + ⋯ + r k k u k + 0 ⋅ u k + 1 + ⋯ + 0 ⋅ u n \mathbf x_k=r_{1k}\mathbf u_1+\cdots+r_{kk}\mathbf u_k+0\cdot\mathbf u_{k+1}+\cdots+0\cdot\mathbf u_n xk=r1ku1+⋯+rkkuk+0⋅uk+1+⋯+0⋅un
于是
x k = Q r k \mathbf x_k=Q\mathbf r_k xk=Qrk
其中 r k = ( r 1 k , ⋯ , r k k , 0 , ⋯ , 0 ) T \mathbf r_k=(r_{1k},\cdots,r_{kk},0,\cdots,0)^T rk=(r1k,⋯,rkk,0,⋯,0)T ,且 r k k ⩾ 0 r_{kk}\geqslant 0 rkk⩾0 (在正交化过程中,若 r k k < 0 r_{kk}<0 rkk<0 ,则 r k k r_{kk} rkk 和 u k \mathbf u_k uk 同乘-1)。取 R = ( r 1 , r 2 , ⋯ , r n ) R=(\mathbf r_1,\mathbf r_2,\cdots,\mathbf r_n) R=(r1,r2,⋯,rn) ,则
A = ( Q r 1 , Q r 2 , ⋯ , Q r n ) = Q R A=(Q\mathbf r_1,Q\mathbf r_2,\cdots,Q\mathbf r_n)=QR A=(Qr1,Qr2,⋯,Qrn)=QR
例:求 A = [ 1 0 0 1 1 0 1 1 1 1 1 1 ] A=\begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix} A= 111101110011 的一个 QR 分解
解:通过施密特正交化方法我们可以得到 col A \text{col }A col A 的一组标准正交基,将这些向量组成矩阵
Q = [ 1 / 2 − 3 / 12 0 1 / 2 1 / 12 − 2 / 6 1 / 2 1 / 12 1 / 6 1 / 2 1 / 12 1 / 6 ] Q=\begin{bmatrix}1/2&-3/\sqrt{12}&0\\1/2&1/\sqrt{12}&-2/\sqrt{6}\\1/2&1/\sqrt{12}&1/\sqrt{6}\\1/2&1/\sqrt{12}&1/\sqrt{6}\end{bmatrix} Q= 1/21/21/21/2−3/121/121/121/120−2/61/61/6
注意到 Q Q Q 是正交矩阵, Q T = Q − 1 Q^T=Q^{-1} QT=Q−1 。所以 R = Q − 1 A = Q T A R=Q^{-1}A=Q^TA R=Q−1A=QTA
R = [ 1 / 2 1 / 2 1 / 2 1 / 2 − 3 / 12 1 / 12 1 / 12 1 / 12 0 − 2 / 6 1 / 6 1 / 6 ] [ 1 0 0 1 1 0 1 1 1 1 1 1 ] = [ 2 3 / 2 1 0 3 / 12 2 / 12 0 0 2 / 6 ] R=\begin{bmatrix}1/2&1/2&1/2&1/2\\ -3/\sqrt{12}&1/\sqrt{12}&1/\sqrt{12}&1/\sqrt{12} \\ 0&-2/\sqrt{6}&1/\sqrt{6}&1/\sqrt{6} \end{bmatrix} \begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix}= \begin{bmatrix}2&3/2&1\\0&3/\sqrt{12}&2/\sqrt{12}\\0&0&2/\sqrt{6} \end{bmatrix} R= 1/2−3/1201/21/12−2/61/21/121/61/21/121/6 111101110011 = 2003/23/12012/122/6
特征值分解
特征值分解是将矩阵分解成特征值和特征向量形式:
A = Q Σ Q − 1 A=Q\Sigma Q^{-1} A=QΣQ−1
其中, Σ = diag ( λ 1 , λ 2 , ⋯ , λ n ) \Sigma=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_n) Σ=diag(λ1,λ2,⋯,λn) 是一个对角阵,其对角线元素是矩阵 A A A 的特征值按降序排列 λ 1 ⩾ λ 2 ⩾ ⋯ ⩾ λ n \lambda_1\geqslant\lambda_2\geqslant\cdots\geqslant\lambda_n λ1⩾λ2⩾⋯⩾λn, Q = ( u 1 , u 2 , … , u n ) Q=(\mathbf u_1,\mathbf u_2,\dots,\mathbf u_n) Q=(u1,u2,…,un) 是特征值对应的特征向量组成的矩阵。

特征值分解后,方阵的幂变得更容易计算
A t = Q Σ t Q − 1 = Q [ λ 1 t ⋱ λ n t ] Q − 1 A^t=Q\Sigma^t Q^{-1}=Q\begin{bmatrix}\lambda_1^t\\&\ddots\\&&\lambda_n^t\end{bmatrix}Q^{-1} At=QΣtQ−1=Q λ1t⋱λnt Q−1
特征值分解可以理解为:先切换基向量,然后伸缩变换,最后再切换回原来的基向量。其中, Σ \Sigma Σ 中的特征向量描述伸缩变换的程度,特征向量描述变换的方向。
特征值分解有一定的局限性,因为它只适用于满秩的方阵。
例:求矩阵 A = [ − 2 1 1 0 2 0 − 4 1 3 ] A=\begin{bmatrix}-2&1&1\\0&2&0\\-4&1&3\end{bmatrix} A= −20−4121103 的特征值分解。
解:矩阵 A A A 的特征多项式为 det ( A − λ I ) = − ( λ − 2 ) 2 ( λ + 1 ) \det(A-\lambda I)=-(\lambda-2)^2(\lambda+1) det(A−λI)=−(λ−2)2(λ+1) 。特征值和特征向量分别为
λ 1 = − 1 : u 1 = [ 1 0 1 ] ; λ 2 = 2 : u 2 = [ 0 1 − 1 ] , u 3 = [ 1 0 4 ] \lambda_1=-1:\mathbf u_1=\begin{bmatrix}1\\0\\1\end{bmatrix};\quad \lambda_2=2:\mathbf u_2=\begin{bmatrix}0\\1\\-1\end{bmatrix}, \mathbf u_3=\begin{bmatrix}1\\0\\4\end{bmatrix} λ1=−1:u1= 101 ;λ2=2:u2= 01−1 ,u3= 104
可通过行变换计算逆矩阵
( Q , I ) = [ 0 1 1 1 0 0 1 0 0 0 1 0 − 1 4 1 0 0 1 ] → [ 1 0 0 0 1 0 0 1 0 − 1 / 3 1 / 3 1 / 3 0 0 1 4 / 3 − 1 / 3 − 1 / 3 ] = ( I , Q − 1 ) (Q,I)=\begin{bmatrix}\begin{array}{ccc:ccc} 0&1&1&1&0&0\\1&0&0&0&1&0\\-1&4&1&0&0&1 \end{array}\end{bmatrix}\to \begin{bmatrix}\begin{array}{ccc:ccc} 1&0&0&0&1&0\\0&1&0&-1/3&1/3&1/3\\0&0&1&4/3&-1/3&-1/3 \end{array}\end{bmatrix}=(I,Q^{-1}) (Q,I)= 01−1104101100010001 → 1000100010−1/34/311/3−1/301/3−1/3 =(I,Q−1)
所以
A = [ 0 1 1 1 0 0 − 1 4 1 ] [ 2 0 0 0 2 0 0 0 − 1 ] [ 0 1 0 − 1 / 3 1 / 3 1 / 3 4 / 3 − 1 / 3 − 1 / 3 ] A=\begin{bmatrix}0&1&1\\1&0&0\\-1&4&1\end{bmatrix} \begin{bmatrix}2&0&0\\0&2&0\\0&0&-1\end{bmatrix} \begin{bmatrix}0&1&0\\-1/3&1/3&1/3\\4/3&-1/3&-1/3\end{bmatrix} A= 01−1104101 20002000−1 0−1/34/311/3−1/301/3−1/3
奇异值分解
奇异值分解
奇异值分解(Singular Value Decomposition, SVD)是线性代数中一种重要的矩阵分解,在生物信息学、信号处理、金融学、统计学等领域有重要应用。
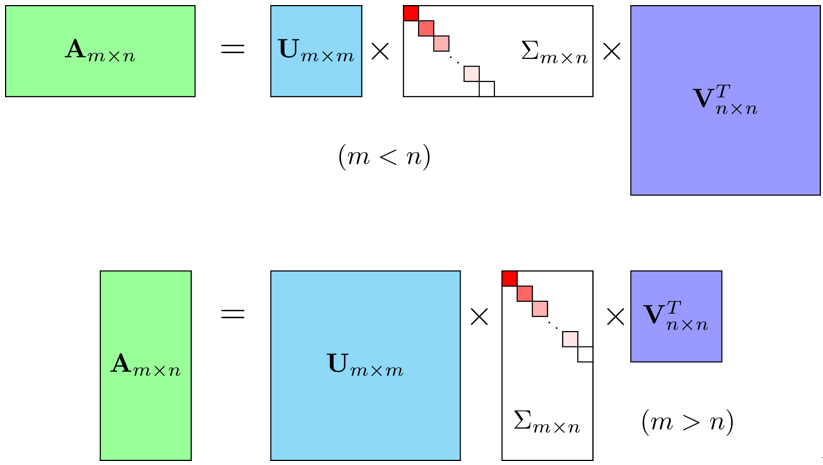
SVD 可以理解为同一线性变换 T : R n ↦ R m T:\R^n\mapsto\R^m T:Rn↦Rm 在不同基下的矩阵表示。假设 Grant 选用标准基,对应的矩阵为 A m × n A_{m\times n} Am×n 。类似于特征值分解, Jennifer 通过选择合适的基向量,对应的矩阵变为简单的长方形对角矩阵 Σ m × n \Sigma_{m\times n} Σm×n,即只有伸缩变换。
假定 Jennifer 使用矩阵 V n = ( v 1 , ⋯ , v n ) V_n=(\mathbf v_1,\cdots,\mathbf v_n) Vn=(v1,⋯,vn) 的列向量作为 R n R^n Rn 的基,使用矩阵 U n = ( u 1 , ⋯ , u m ) U_n=(\mathbf u_1,\cdots,\mathbf u_m) Un=(u1,⋯,um)的列向量作为 R m R^m Rm 的基 。那么,对于 Jennifer 视角下的向量 x ∈ R n \mathbf x\in R^n x∈Rn
- 同样的向量,用 Grant 的坐标系表示为 V x V\mathbf x Vx
- 用 Grant 的语言描述变换后的向量 A V x AV\mathbf x AVx
- 将变换后的结果变回 Jennifer 的坐标系 U − 1 A V x U^{-1}AV\mathbf x U−1AVx
于是,我们得到同一个线性变换 T T T 在 Jennifer 的坐标系下对应的矩阵 Σ = U − 1 A V \Sigma=U^{-1}AV Σ=U−1AV ,也可理解为矩阵 A A A 分解为 A m × n = U m Σ m × n V n − 1 A_{m\times n}=U_m\Sigma_{m\times n}V^{-1}_n Am×n=UmΣm×nVn−1 。
接下来,自然是探讨上述矩阵分解的适用条件。
注意到
A T A = ( U Σ V − 1 ) T ( U Σ V − 1 ) = V − T Σ T U T U Σ V − 1 A^TA=(U\Sigma V^{-1})^T(U\Sigma V^{-1})=V^{-T}\Sigma^TU^TU\Sigma V^{-1} ATA=(UΣV−1)T(UΣV−1)=V−TΣTUTUΣV−1
不妨取 U , V U,V U,V 为单位正交基,即 U , V U,V U,V 为正交矩阵 U T U = I , V T V = I U^TU=I,V^TV=I UTU=I,VTV=I ,则
A T A = V Σ T Σ V T A^TA=V\Sigma^T\Sigma V^T ATA=VΣTΣVT
于是,可知 V V V 的列向量为 A T A A^TA ATA 的特征向量, Σ T Σ \Sigma^T\Sigma ΣTΣ 为 n n n 阶对角阵,其对角元素为 A T A A^TA ATA 的特征值。事实上 A T A A^TA ATA 为对称阵,必定存在正交矩阵 V V V 相似对角化。
同理
A A T = U Σ Σ T U T AA^T=U\Sigma\Sigma^T U^T AAT=UΣΣTUT
可知 U U U 的列向量为 A A T AA^T AAT 的特征向量, Σ Σ T \Sigma\Sigma^T ΣΣT 为 m m m 阶对角阵,其对角元素为 A A T AA^T AAT 的特征值。矩阵 A T A A^TA ATA 为对称阵,必定存在正交矩阵 U U U 相似对角化。
目前 U , V U,V U,V 我们都求出来了,只剩下求出长方形对角矩阵 Σ \Sigma Σ 。根据 Sylvester降幂公式, A T A A^TA ATA 和 A A T AA^T AAT 有相同的非零特征值。
令 Σ = [ Λ r O O O ] \Sigma=\begin{bmatrix}\Lambda_r&O\\O&O\end{bmatrix} Σ=[ΛrOOO] ,其中 Λ r = diag ( σ 1 , ⋯ , σ r ) \Lambda_r=\text{diag}(\sigma_1,\cdots,\sigma_r) Λr=diag(σ1,⋯,σr) 。则
Σ T Σ = [ Λ r 2 O O O ] n , Σ Σ T = [ Λ r 2 O O O ] m \Sigma^T\Sigma=\begin{bmatrix}\Lambda_r^2&O\\O&O\end{bmatrix}_n,\quad \Sigma\Sigma^T=\begin{bmatrix}\Lambda_r^2&O\\O&O\end{bmatrix}_m ΣTΣ=[Λr2OOO]n,ΣΣT=[Λr2OOO]m
其中 Λ r 2 = diag ( σ 1 2 , ⋯ , σ r 2 ) \Lambda_r^2=\text{diag}(\sigma_1^2,\cdots,\sigma_r^2) Λr2=diag(σ12,⋯,σr2) 。因此,矩阵 Σ \Sigma Σ 的对角元素是 A T A A^TA ATA 和 A A T AA^T AAT 的特征值 λ j \lambda_j λj 的平方根
σ j = λ j \sigma_j=\sqrt{\lambda_j} σj=λj
综上,任意矩阵均可奇异值分解。

定义:SVD是指将秩为 r r r 的 m × n m\times n m×n 矩阵 A A A分解为
A = U Σ V T A=U\Sigma V^T A=UΣVT
其中 U U U 为 m m m 阶正交阵, V V V 为 n n n 阶正交阵, Σ \Sigma Σ 为 m × n m\times n m×n 维长方形对角矩阵,对角元素称为矩阵 A A A 的奇异值,一般按降序排列 σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ r > 0 \sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_r>0 σ1⩾σ2⩾⋯⩾σr>0 ,这样 Σ \Sigma Σ 就唯一确定了。矩阵 U U U 的列向量称为左奇异向量(left singular vector),矩阵 V V V 的列向量称为右奇异向量(right singular vector)。
例:这里我们用一个简单的矩阵来说明奇异值分解的步骤。求矩阵 A = [ 0 1 1 1 1 0 ] A=\begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix} A= 011110 的奇异值分解
解:首先求出对称阵 A T A A^TA ATA 和 A A T AA^T AAT
A T A = [ 0 1 1 1 1 0 ] [ 0 1 1 1 1 0 ] = [ 2 1 1 2 ] A A T = [ 0 1 1 1 1 0 ] [ 0 1 1 1 1 0 ] = [ 1 1 0 1 2 1 0 1 1 ] A^TA=\begin{bmatrix}0&1&1\\1&1&0\end{bmatrix} \begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix}= \begin{bmatrix}2&1\\1&2\end{bmatrix} \\ AA^T=\begin{bmatrix}0&1\\1&1\\1&0\end{bmatrix} \begin{bmatrix}0&1&1\\1&1&0\end{bmatrix}= \begin{bmatrix}1&1&0\\1&2&1\\0&1&1\end{bmatrix} ATA=[011110] 011110 =[2112]AAT= 011110 [011110]= 110121011
然后求出 A T A A^TA ATA 的特征值和特征向量
λ 1 = 3 : v 1 = [ 1 / 2 1 / 2 ] ; λ 2 = 1 : v 2 = [ − 1 / 2 1 / 2 ] \lambda_1=3:\mathbf v_1=\begin{bmatrix}1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix};\quad \lambda_2=1:\mathbf v_2=\begin{bmatrix}-1/\sqrt{2}\\1/\sqrt{2}\end{bmatrix} λ1=3:v1=[1/21/2];λ2=1:v2=[−1/21/2]
求出 A A T AA^T AAT 的特征值和特征向量
λ 1 = 3 : u 1 = [ 1 / 6 2 / 6 1 / 6 ] ; λ 2 = 1 : u 2 = [ 1 / 2 0 − 1 / 2 ] ; λ 3 = 0 : u 3 = [ 1 / 3 − 1 / 3 1 / 3 ] ; \lambda_1=3:\mathbf u_1=\begin{bmatrix}1/\sqrt{6}\\2/\sqrt{6}\\1/\sqrt{6}\end{bmatrix};\quad \lambda_2=1:\mathbf u_2=\begin{bmatrix}1/\sqrt{2}\\0\\-1/\sqrt{2}\end{bmatrix};\quad \lambda_3=0:\mathbf u_3=\begin{bmatrix}1/\sqrt{3}\\-1/\sqrt{3}\\1/\sqrt{3}\end{bmatrix}; λ1=3:u1= 1/62/61/6 ;λ2=1:u2= 1/20−1/2 ;λ3=0:u3= 1/3−1/31/3 ;
其次可以利用 σ i = λ i \sigma_i=\sqrt{\lambda_i} σi=λi 求出奇异值 3 , 1 \sqrt{3},1 3,1
最终得到 A A A的奇异值分解
A = U Σ V T = [ 1 / 6 1 / 2 1 / 3 2 / 6 0 − 1 / 3 1 / 6 − 1 / 2 1 / 3 ] [ 3 0 0 1 0 0 ] [ 1 / 2 1 / 2 − 1 / 2 1 / 2 ] A=U\Sigma V^T=\begin{bmatrix}1/\sqrt{6}&1/\sqrt{2}&1/\sqrt{3}\\2/\sqrt{6}&0&-1/\sqrt{3}\\1/\sqrt{6}&-1/\sqrt{2}&1/\sqrt{3}\end{bmatrix} \begin{bmatrix}\sqrt{3}&0\\0&1\\0&0\end{bmatrix} \begin{bmatrix}1/\sqrt{2}&1/\sqrt{2}\\-1/\sqrt{2}&1/\sqrt{2}\end{bmatrix} A=UΣVT= 1/62/61/61/20−1/21/3−1/31/3 300010 [1/2−1/21/21/2]
矩阵的基本子空间
设矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT ,有 r r r 个不为零的奇异值,则可以得到矩阵 A A A 的四个基本子空间:
- 正交阵 U U U 的前 r r r 列是 col A \text{col }A col A 的一组单位正交基
- 正交阵 U U U 的后 m − r m-r m−r 列是 ker A T \ker A^T kerAT 的一组单位正交基
- 正交阵 V V V 的前 r r r 列是 col A T \text{col }A^T col AT 的一组单位正交基
- 正交阵 V V V 的后 n − r n-r n−r 列是 ker A \ker A kerA 的一组单位正交基
A ( v 1 , ⋯ , v r ⏟ col A T , v r + 1 ⋯ v n ⏟ ker A ) = ( u 1 , ⋯ , u r ⏟ col A , u r + 1 ⋯ u m ⏟ ker A T ) [ σ 1 ⋱ σ r O ] ⏟ Σ m × n A(\underbrace{\mathbf v_1,\cdots,\mathbf v_r}_{\text{col }A^T},\underbrace{\mathbf v_{r+1}\cdots\mathbf v_n}_{\ker A})= (\underbrace{\mathbf u_1,\cdots,\mathbf u_r}_{\text{col }A},\underbrace{\mathbf u_{r+1}\cdots\mathbf u_m}_{\ker A^T}) \underbrace{\begin{bmatrix}\sigma_1\\&\ddots\\&&\sigma_r\\&&&O \end{bmatrix}}_{\Sigma_{m\times n}} A(col AT v1,⋯,vr,kerA vr+1⋯vn)=(col A u1,⋯,ur,kerAT ur+1⋯um)Σm×n σ1⋱σrO
证:易知 A V = U Σ AV=U\Sigma AV=UΣ ,即
{ A v i = σ i u i , 1 ⩽ i ⩽ r A v i = 0 , r < i ⩽ n \begin{cases} A\mathbf v_i=\sigma_i\mathbf u_i, &1\leqslant i\leqslant r \\ A\mathbf v_i=0, &r< i\leqslant n \end{cases} {Avi=σiui,Avi=0,1⩽i⩽rr<i⩽n
取 v 1 , ⋯ , v n \mathbf v_1,\cdots,\mathbf v_n v1,⋯,vn 为 R n \R^n Rn 的单位正交基,对于 ∀ x ∈ R n \forall\mathbf x\in \R^n ∀x∈Rn ,可以写出 x = c 1 v 1 + ⋯ + c n v n \mathbf x=c_1\mathbf v_1+\cdots+c_n\mathbf v_n x=c1v1+⋯+cnvn,于是
A x = c 1 A v 1 + ⋯ + c r A v r + c r + 1 A v r + 1 + ⋯ + c n v n = c 1 σ 1 u 1 + ⋯ + c r σ 1 u r + 0 + ⋯ + 0 \begin{aligned} A\mathbf x&=c_1A\mathbf v_1+\cdots+c_rA\mathbf v_r+c_{r+1}A\mathbf v_{r+1}+\cdots+c_n\mathbf v_n \\ &=c_1\sigma_1\mathbf u_1+\cdots+c_r\sigma_1\mathbf u_r+0+\cdots+0 \end{aligned} Ax=c1Av1+⋯+crAvr+cr+1Avr+1+⋯+cnvn=c1σ1u1+⋯+crσ1ur+0+⋯+0
所以 A x ∈ span { u 1 , ⋯ , u r } A\mathbf x\in\text{span}\{\mathbf u_1,\cdots,\mathbf u_r\} Ax∈span{u1,⋯,ur} ,这说明矩阵 U U U 的前 r r r 列是 col A \text{col }A col A 的一组单位正交基,因此 rank A = r \text{rank }A=r rank A=r 。同时可知,对于任意的 x ∈ span { v r + 1 , ⋯ , v n } ⟺ A x = 0 \mathbf x\in\text{span}\{\mathbf v_{r+1},\cdots,\mathbf v_n\}\iff A\mathbf x=0 x∈span{vr+1,⋯,vn}⟺Ax=0 ,于是 V V V 的后 n − r n-r n−r 列是 ker A \ker A kerA 的一组单位正交基。
同样通过 A T U = V Σ A^TU=V\Sigma ATU=VΣ 可说明 V V V 的前 r r r 列是 col A T \text{col }A^T col AT 的一组单位正交基, U U U 的后 m − r m-r m−r 列是 ker A T \ker A^T kerAT 的一组单位正交基。
奇异值分解的性质
设矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT ,秩 rank A = r \text{rank }A=r rank A=r ,分别将 U , Σ , V U,\Sigma,V U,Σ,V 进行分块
U = ( U r , U m − r ) V = ( V r , V n − r ) Σ = [ Λ r O O O ] U=(U_r,U_{m-r}) \\ V=(V_r,V_{n-r}) \\ \Sigma=\begin{bmatrix}\Lambda_r&O\\O&O\end{bmatrix} U=(Ur,Um−r)V=(Vr,Vn−r)Σ=[ΛrOOO]
其中 U r = ( u 1 , ⋯ , u r ) U_r=(\mathbf u_1,\cdots,\mathbf u_r) Ur=(u1,⋯,ur) 为 m × r m\times r m×r维矩阵, V r = ( v 1 , ⋯ , v r ) V_r=(\mathbf v_1,\cdots,\mathbf v_r) Vr=(v1,⋯,vr) 为 n × r n\times r n×r维矩阵, Λ r = diag ( σ 1 , ⋯ , σ r ) \Lambda_r=\text{diag}(\sigma_1,\cdots,\sigma_r) Λr=diag(σ1,⋯,σr) 为 r r r 阶对角阵。应用矩阵乘法的性质,奇异值分解可以简化为
A = U r Λ r V r T A=U_r\Lambda_r V^T_r A=UrΛrVrT
这个分解称为简化奇异值分解。
性质:
- 奇异值分解可理解为将线性变换分解为三个简单的变换:正交变换 V T V^T VT,伸缩变换 Σ \Sigma Σ 和正交变换 U U U 。
- 矩阵 A A A 的奇异值分解中,奇异值是唯一的,但矩阵 U , V U,V U,V 不是唯一的。
- 令 λ \lambda λ 为 A T A A^TA ATA 的一个特征值, v \mathbf v v 是对应的特征向量,则
∥ A v ∥ 2 = v T A T A v = λ v T v = λ ∥ v ∥ \|A\mathbf v\|^2=\mathbf v^TA^TA\mathbf v=\lambda\mathbf v^T\mathbf v=\lambda\|\mathbf v\| ∥Av∥2=vTATAv=λvTv=λ∥v∥ - 易知 A V = U Σ AV=U\Sigma AV=UΣ 或 A T U = V Σ T A^TU=V\Sigma^T ATU=VΣT,则左奇异向量和右奇异向量存在关系
A v j = σ j u j A T u j = σ j v j A\mathbf v_j=\sigma_j\mathbf u_j \\ A^T\mathbf u_j=\sigma_j\mathbf v_j Avj=σjujATuj=σjvj
矩阵的外积展开式
矩阵 A = U Σ V T A=U\Sigma V^T A=UΣVT 可展开为若干个秩为1的 m × n m\times n m×n矩阵之和
A = σ 1 u 1 v 1 T + σ 2 u 2 v 2 T + ⋯ + σ r u r v r T A=\sigma_1\mathbf u_1\mathbf v_1^T+\sigma_2\mathbf u_2\mathbf v_2^T+\cdots+\sigma_r\mathbf u_r\mathbf v_r^T A=σ1u1v1T+σ2u2v2T+⋯+σrurvrT
上式称为矩阵 A A A 的外积展开式。
在长方形对角矩阵 Σ \Sigma Σ 中奇异值按从大到小的顺序排列 σ 1 ⩾ σ 2 ⩾ ⋯ ⩾ σ r > 0 \sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_r>0 σ1⩾σ2⩾⋯⩾σr>0 。在很多情况下,由于奇异值递减很快,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上。因此,我们可以用前面 k k k 个大的奇异值来近似描述矩阵。
奇异值分解也是一种矩阵近似的方法,这个近似是在矩阵范数意义下的近似。矩阵范数是向量范数的直接推广。
∥ A ∥ 2 = ( ∑ j = 1 n ∑ i = 1 m ∣ a i j ∣ 2 ) 1 / 2 \|A\|_2=(\sum_{j=1}^{n}\sum_{i=1}^{m} |a_{ij}|^2)^{1/2} ∥A∥2=(j=1∑ni=1∑m∣aij∣2)1/2
可以证明
∥ A ∥ 2 2 = tr ( A T A ) = ∑ i = 1 r σ i 2 \|A\|_2^2=\text{tr}(A^TA)= \sum_{i=1}^{r} \sigma_i^2 ∥A∥22=tr(ATA)=i=1∑rσi2
设矩阵
A k = ∑ i = 1 k σ i u i v i T A_k=\sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i^T Ak=i=1∑kσiuiviT
则 A k A_k Ak 的秩为 k k k ,矩阵 A k A_k Ak 称为 A A A 的截断奇异值分解。并且 A k A_k Ak 是秩为 k k k 时的最优近似,即 A k A_k Ak 为以下最优问题的解
min ∥ A − X ∥ 2 s.t. rank A = k \min\|A-X\|_2 \\ \text{s.t. rank }A=k min∥A−X∥2s.t. rank A=k
上式称为低秩近似(low-rank approximation)。于是奇异值分解可近似为
A ≈ ∑ i = 1 k σ i u i v i T = U m × k Σ k × k V n × k T A\approx \sum_{i=1}^k\sigma_i\mathbf u_i\mathbf v_i^T=U_{m\times k}\Sigma_{k\times k}V_{n\times k}^T A≈i=1∑kσiuiviT=Um×kΣk×kVn×kT
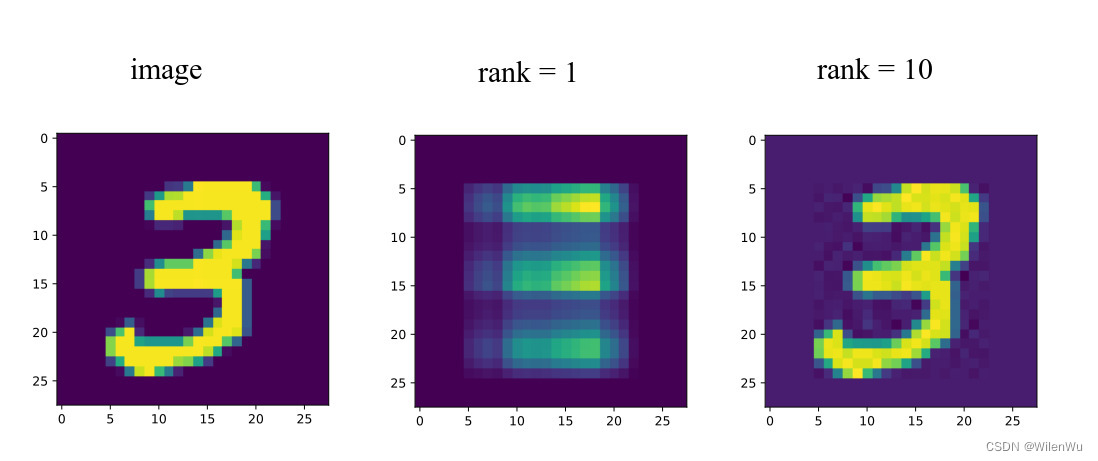
其中 k k k 是一个远远小于 m m m和 n n n的数,从计算机内存的角度来说,矩阵左(右)奇异向量和奇异值的存储要远远小于矩阵 A A A的。所以,截断奇异值分解就是在计算精度和时间空间之间做选择。如果 k k k越大,右边的三个矩阵相乘的结果越接近于 A A A。
截断奇异值分解常用于图像压缩,如下图
相关文章:

线性代数的本质(十)——矩阵分解
文章目录 矩阵分解LU分解QR分解特征值分解奇异值分解奇异值分解矩阵的基本子空间奇异值分解的性质矩阵的外积展开式 矩阵分解 矩阵的因式分解是把矩阵表示为多个矩阵的乘积,这种结构更便于理解和计算。 LU分解 设 A A A 是 m n m\times n mn 矩阵,…...

vue实现鼠标拖拽div左右移动的功能
直接代码: <template><div class"demo"><div class"third-part" id"发展历程"><div class"title">发展历程</div><div class"content" id"nav" v-if"dataList…...
基于Python和mysql开发的商城购物管理系统分为前后端(源码+数据库+程序配置说明书+程序使用说明书)
一、项目简介 本项目是一套基于Python和mysql开发的商城购物管理系统,主要针对计算机相关专业的正在做毕设的学生与需要项目实战练习的Python学习者。 包含:项目源码、项目文档、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过…...

MySQL内外连接、索引特性
目录 内连接 外连接 索引特性 理解索引 删除索引 MySQL内外连接是一种用于联接两个或多个表的操作。内连接只返回满足连接条件的行,外连接返回满足条件和不满足条件的行。 内连接 SQL如下: SELECT ... FROM t1 INNER JOIN t2 ON 连接条件 [INNER …...

滚动条设置
不同浏览器滚动条样式及滚动定位 是否可以滚动 overflow:scroll overflow:autooverflow:scroll – 只有超出了盒子才会有滚动条 overflow:auto – 一直有滚动的盒子,只是超出了盒子才会出现滚动条滑块,可以滚动 谷歌浏览器滚动…...
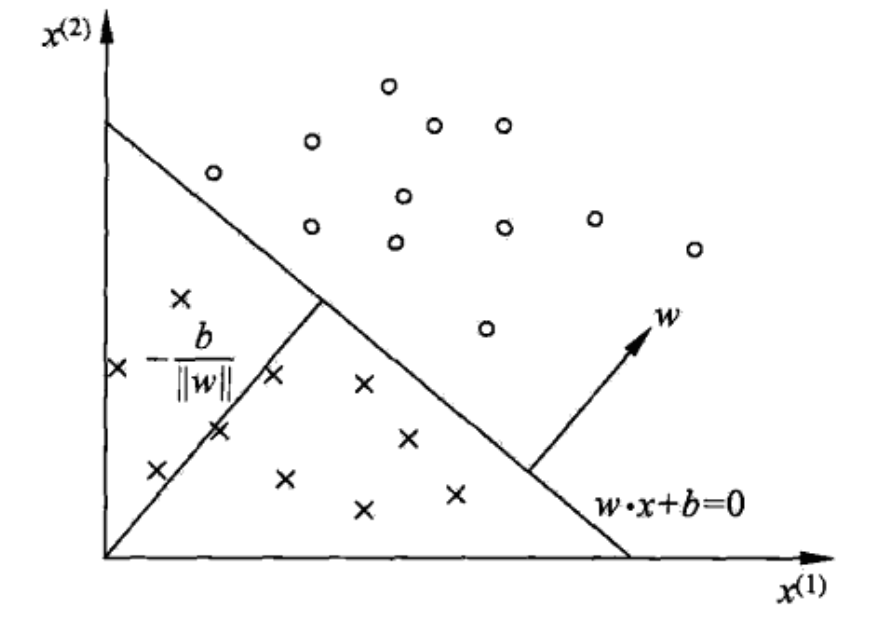
【AI】机器学习——感知机
文章目录 4.1 感知机基本概念4.2 策略4.2.1 数据集的线性可分性4.2.2 学习策略目标损失函数的构造关于距离的解释 4.3 算法4.3.1 原始形式损失函数的梯度下降法 4.3.2 PLA例题4.3.3 算法收敛性 4.4 PLA对偶形式4.4.1 原始PLA分析4.4.2 PLA对偶形式4.4.3 优点 4.1 感知机基本概念…...

蓝牙遥控器在T2-U上的应用
文章目录 简介优势使用流程示例代码遥控器命令表遥控器代码实现开启遥控器配对功能运行 简介 Tuya beacon 协议是基于 BLE 广播通信技术,完善配对解绑、组包拆包、群组管理、加密解密、安全策略,形成的一种轻量、安全的可接入涂鸦云的蓝牙协议。 蓝牙 …...
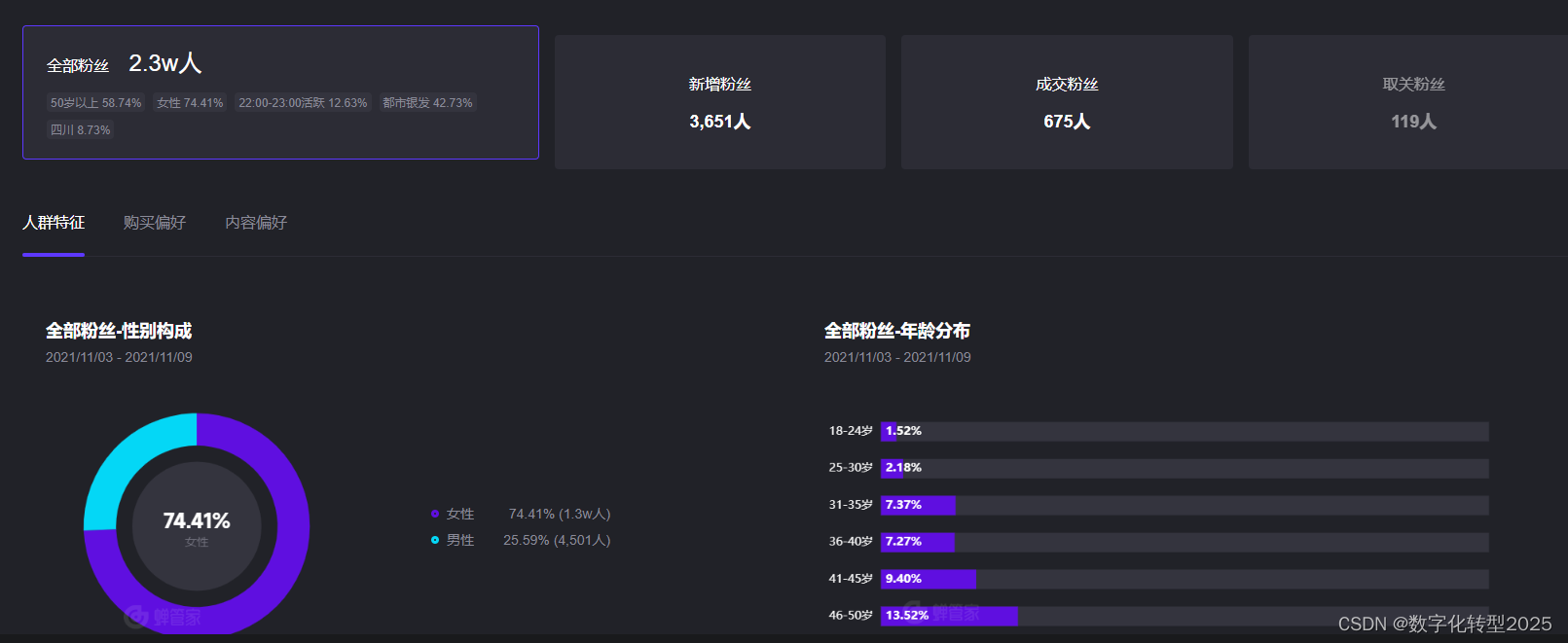
数据驱动的数字营销与消费者运营
引言:基于海洋馆文旅企业在推广宣传中,如何通过指标体系量化分析广告收益对业务带来的收益价值的思考? 第一部分:前链路引流投放的策略与实战 1.1 动态广告的实现: 偶然与必然 动态广告是一种基于实时数据和用户行为的广告形式,它…...

Qt点亮I.MX6U开发板的一个LED
本篇开始将会介绍与开发版相关的Qt项目,首先从点亮一个LED开始。I.MX6U和STM32MP157的相关信息都会用到,但是后期还是将I.MX6U的学习作为重点。当然其他开发版的开发也可以参考本博文。 文章目录 1. Qt是如何操控开发板上的一个LED2. 出厂内核设备树中注…...

网络摄像头-流媒体服务器-视频流客户端
取电脑的视频流 当涉及交通事件检测算法和摄像头视频数据处理时,涉及的代码案例可能会非常复杂,因为这涉及到多个组件和技术。以下是一个简单的Python代码示例,演示如何使用OpenCV库捕获摄像头视频流并进行实时车辆检测,这是一个…...
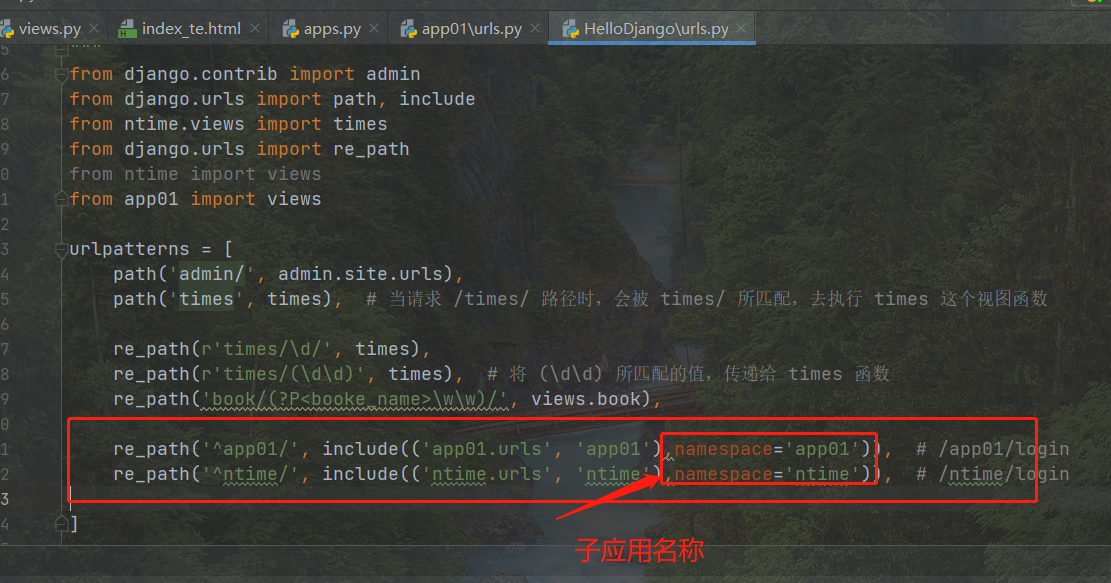
Django05_反向解析
Django05_反向解析 5.1 反向解析概述 随着功能的不断扩展,路由层的 url 发生变化,就需要去更改对应的视图层和模板层的 url,非常麻烦,不便维护。这个时候我们可以通过反向解析,将 url解析成对应的 试图函数 通过 path…...

基于HTML、CSS和JavaScript制作一个中秋节倒计时网页
💂 个人网站:【工具大全】【游戏大全】【神级源码资源网】🤟 前端学习课程:👉【28个案例趣学前端】【400个JS面试题】💅 寻找学习交流、摸鱼划水的小伙伴,请点击【摸鱼学习交流群】 这个项目使用HTML、CSS和…...

富斯I6刷10通道固件
使用USB转串口模块刷写10通道固件 一、下载固件 1. 十通道英文固件 下载地址: https://github.com/benb0jangles/FlySky-i6-Mod-/tree/master 选择 FlySky-i6-Mod–master \ 10ch Mod i6 Updater \ 10ch_MOD_i6_Programmer_V1 路径下的文件,亲测可用。 2. 原版六通道中…...

vector的模拟实现 总结
vector的模拟实现 总结 vector.hTest.cpp vector.h 1、迭代器的实现 #pragma oncenamespace JPC {template<class T>class vector{public://对于存储空间是连续的结构而言,可以用原身指针来 模拟实现 迭代器。typedef T* iterator;typedef const T* const_i…...

k8s中的有状态,无状态,pv、pvc等
数据库是一个典型的有状态服务,他的部署和无状态服务是不一样的。 PostgresSQL----基于Kubernetes部署PostgresSQL-CSDN博客 一、创建SC、PV和PVC存储对象 二、部署PostgresSQL Volume Kubernetes 中文指南——云原生应用架构实战手册 有状态应用: …...
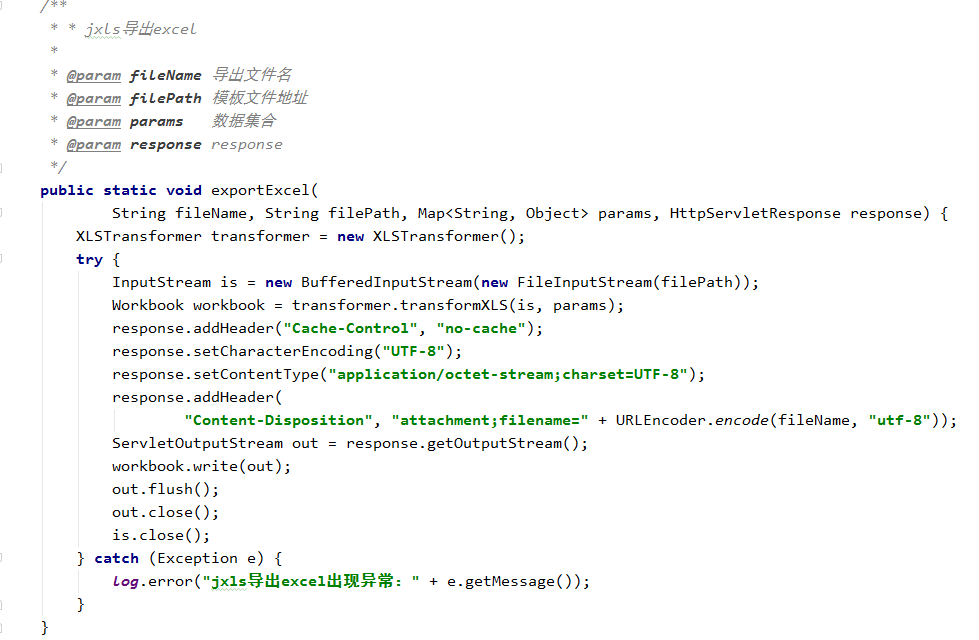
springboot+jxls复杂excel模板导出
JXLS 是基于 Jakarta POI API 的 Excel 报表生成工具,可以生成精美的 Excel 格式报表。它采用标签的方式,类似 JSP 标签,写一个 Excel 模板,然后生成报表,非常灵活,简单! Java 有一些用于创建 …...
用selenium webdriver获取网站cookie后,实现免登录上网站
以csdn为例,代码分为两部分。 一、csdn_get_cookies.py为半手动登录网站后获取cookies 二、csdn_use_cookies.py为使用获取到的cookies免登录上网站 #获取登录cookiesfrom selenium import webdriver import jsoncsdn_driver webdriver.Chrome() url "htt…...

如何使用Java进行安全测试?
要使用Java进行安全测试,可以按照以下步骤进行: 确定测试目标:首先,明确要测试的应用程序或系统的安全目标和需求。确定要测试的安全方面,如身份验证、授权、输入验证、安全配置等。 了解安全测试知识:熟悉…...
)
Linux之Socket函数(详细篇)
本篇是基于Linux man手册的一些总结 socket作用: create an endpoint for communication 函数结构 c #include <sys/types.h> /* See NOTES */ #include <sys/socket.h> int socket(int domain, int type, int protocol); 描述 socket() …...
Dajngo06_Template模板
Dajngo06_Template模板 6.1 Template模板概述 模板引擎是一种可以让开发者把服务端数据填充到html网页中完成渲染效果的技术 静态网页:页面上的数据都是写死的,万年不变 动态网页:页面上的数据是从后端动态获取的(后端获取数据库…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

GruntJS-前端自动化任务运行器从入门到实战
Grunt 完全指南:从入门到实战 一、Grunt 是什么? Grunt是一个基于 Node.js 的前端自动化任务运行器,主要用于自动化执行项目开发中重复性高的任务,例如文件压缩、代码编译、语法检查、单元测试、文件合并等。通过配置简洁的任务…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

【java面试】微服务篇
【java面试】微服务篇 一、总体框架二、Springcloud(一)Springcloud五大组件(二)服务注册和发现1、Eureka2、Nacos (三)负载均衡1、Ribbon负载均衡流程2、Ribbon负载均衡策略3、自定义负载均衡策略4、总结 …...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...

LangChain【6】之输出解析器:结构化LLM响应的关键工具
文章目录 一 LangChain输出解析器概述1.1 什么是输出解析器?1.2 主要功能与工作原理1.3 常用解析器类型 二 主要输出解析器类型2.1 Pydantic/Json输出解析器2.2 结构化输出解析器2.3 列表解析器2.4 日期解析器2.5 Json输出解析器2.6 xml输出解析器 三 高级使用技巧3…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
