【线性代数】沉浸式线性代数在线学习网站
地址:http://immersivemath.com/ila/index.html
这是全球第一本带交互式图形的线性代数教材,作者是 J. Ström, K. Åström, and T. Akenine-Möller。
全书一共十章,各章节内容如下:

接下来我将对各章节进行简单的总结,另外请注意,阅读过程中请一定不要忘记各章节提供的的可交互图表。
第一章:简介
第一章主要交代了两件事情,第一个是关于符号说明,这个几乎在所有书籍中都有,主要就是告诉你用什么符号表示向量,用什么符号表示矩阵等等。
第二个事情就是回顾了一下三角函数的知识,不要惊讶为什么几何学的东西会出现在这里,三角函数在很多领域都有所应用,在机器学习领域,可以用来计算向量的余弦相似性,而余弦相似性又可以作为目标函数的一种评价指标。
第二章:向量
向量可以说是线性代数中最基础的东西了,就连线性代数的另一大主角矩阵也可以看作是向量的排列组合。
直白地讲,向量就是一组数字的集合,向量存在的最大意义是它们提供了一种有效的数学工具,用于描述和处理现实世界中的各种实体,并在向量空间中发掘实体间的各种关系。
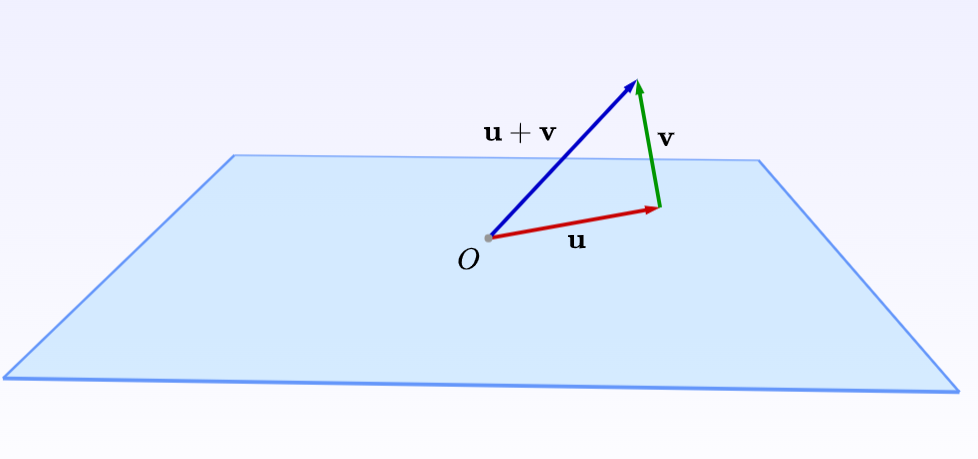
第三章:向量的点积
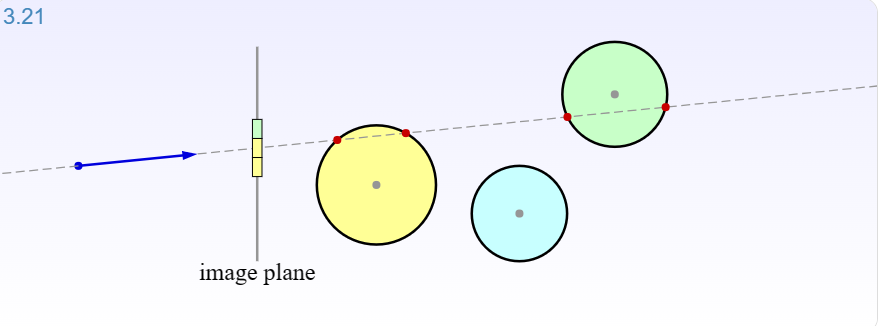
这是继向量加法,向量与标量乘法后,另一个重要的向量操作,向量的点积是两个向量之间的乘法运算,结果是它们对应分量的乘积之和。其作用是计算向量之间的夹角、判断正交性、进行投影和分解、计算相似性和相关性等。
向量的点积是非常重要且经常使用的概念,例如,计算机图形学中光线追踪算法。
第四章:向量的叉积
这是继向量加法,向量与标量乘法,向量点积后,最后一个重要的向量操作,与点积结果为标量不同,叉积的结果仍然是一个向量,也就是说比点点积多了一个方向信息。
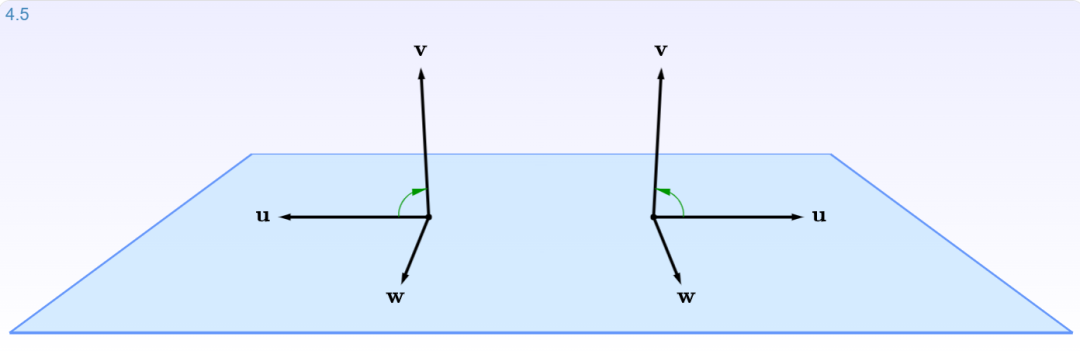
举个应用的例子,计算四面体的体积。
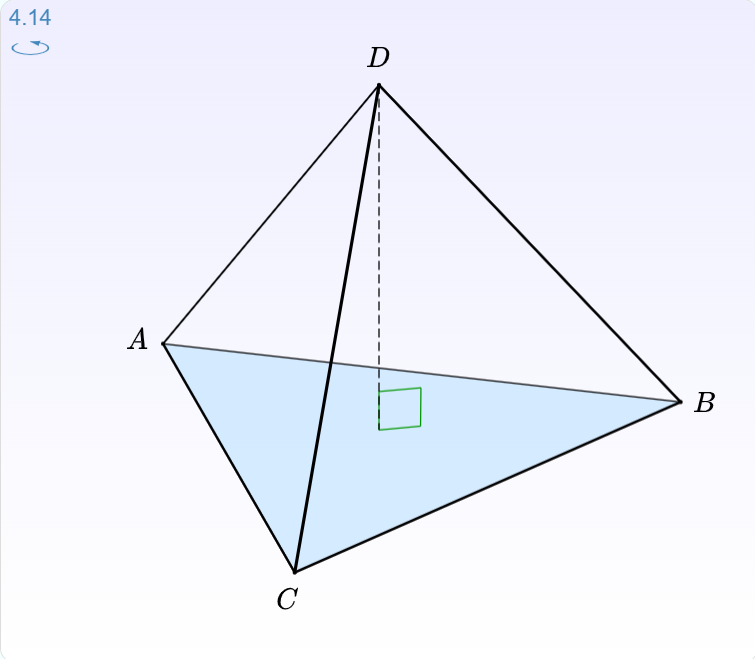
用四个点表示成三个向量。
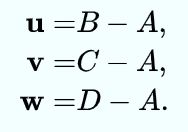
则四面体的体积为:
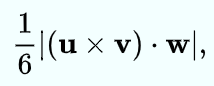
第五章:高斯消元
高斯消元是一种求解线性方程组的方法,也可以用于求矩阵的逆,其实我们在小学就接触过高斯消元,只不过小学学的都是有唯一解的二元一次方程组。
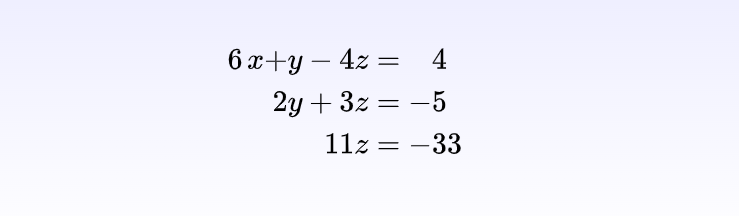
本章节提供了一个实际应用的例子:视频压缩,大家可以研究一下。

第六章:矩阵
矩阵是线性代数中,除向量外的另一大主角,可以从两方面看待矩阵,一方面是静止的,例如,一幅图像可以用矩阵表示,另一方面是动态的,例如可以用矩阵表示一个变换。
对于矩阵,可以去探索一些属性,例如,对于图像进行主成分分析,就能实现降维的目的。计算矩阵的逆,就能快速求解线性方程组。分解矩阵,就能将复杂的问题简化。

第七章:矩阵的行列式
矩阵的行列式是一个方阵所对应的一个标量值。行列式可以看作是矩阵的一个重要属性,根据行列式的值可以进一步判断矩阵是否可逆,线性方程组的解的情况,计算特征值和特征向量等等。
第八章:矩阵的秩
矩阵的秩也可以看作是矩阵的一个非常重要的性质,矩阵的秩是指矩阵中线性独立的行或列的最大数量,也可以理解为矩阵中非零行(或列)的个数。
通过矩阵的秩可以判断矩阵行向量或者列向量的相关性,方程组解的存在性,矩阵的可逆性,以及特征值和特征向量的计算等,
本章提供了一个通过声音恢复结构的例子。

第九章:线性映射
线性映射是指在向量空间之间进行的一种特殊的映射关系,它保持向量的线性组合性质。简而言之,线性映射是指满足加法和数乘运算规则的映射。
具体来说,设有两个向量空间 V 和 W,一个映射 T: V → W 被称为线性映射,如果对于任意向量 u、v ∈ V 和标量 c,满足以下两个条件:
加法性:T(u + v) = T(u) + T(v)。即线性映射对向量的加法保持性质,映射后的结果等于分别映射后的结果相加。
数乘性:T(cu) = cT(u)。即线性映射对向量的数乘保持性质,映射后的结果等于数乘后再进行映射。
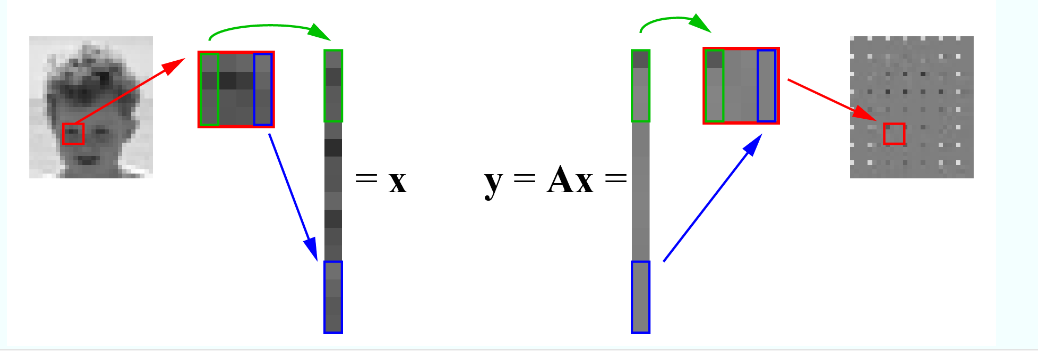
线性系统的性质就决定了其不能表示复杂映射能力,如果要想表示复杂映射关系,就要考虑非线性映射。这也是为什么要在神经网络中加入激活函数的原因。
第十章:特征值与特征向量
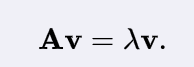
它是矩阵最重要的属性,没有之一。本章提供的例子也很经典。
特征脸

PageRank中稳态向量的求解
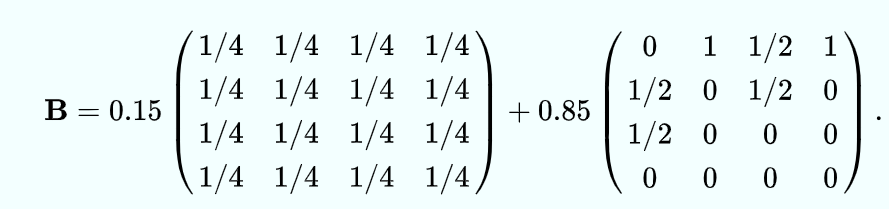
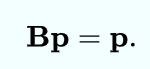
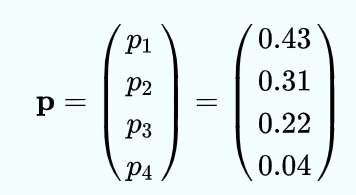
相关文章:
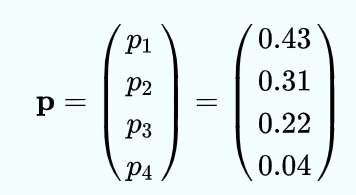
【线性代数】沉浸式线性代数在线学习网站
地址:http://immersivemath.com/ila/index.html 这是全球第一本带交互式图形的线性代数教材,作者是 J. Strm, K. strm, and T. Akenine-Mller。 全书一共十章,各章节内容如下: 接下来我将对各章节进行简单的总结,另外…...

Kotlin中特性、数据类、伴生对象、顶层函数
Kotlin中的函数参数和属性声明 在 Kotlin 中,函数参数和属性有不同的声明方式和行为。这些特性使得 Kotlin 代码更加安全、易于理解和维护。 函数参数的只读性 fun sum(a: Int, b: Int): Int {var modifiedA aif (modifiedA > 0) {modifiedA 1}//三元表达式v…...

《PostgreSQL物化视图:创建、维护与应用》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

shell脚本之test命令
shell脚本之test命令 数值比较:2. 字符串比较:3. 文件测试:4. 逻辑操作:5. 其他测试: test命令在Shell脚本中用于进行条件测试和条件判断。它用于检查文件、字符串和数值的各种条件,并返回一个状态码&#…...

JAVA设计模式8:装饰模式,动态地将责任附加到对象上,扩展对象的功能
作者主页:Designer 小郑 作者简介:3年JAVA全栈开发经验,专注JAVA技术、系统定制、远程指导,致力于企业数字化转型,CSDN博客专家,阿里云社区专家博主,蓝桥云课讲师。 目录 一、什么是装饰模式二、…...

Linux学习之MySQL备份
xtrabackup资源下载 完全备份与恢复 # 1.物理备份与恢复 # 冷备份,需停止数据库服务 适合线下服务器。 [rootmysql50 ~]# systemctl stop mysqld [rootmysql50 ~]# mkdir /bakdir [rootmysql50 ~]# cp -r /var/lib/mysql /bakdir/mysql.bak [rootmysql50 ~]# cd /…...
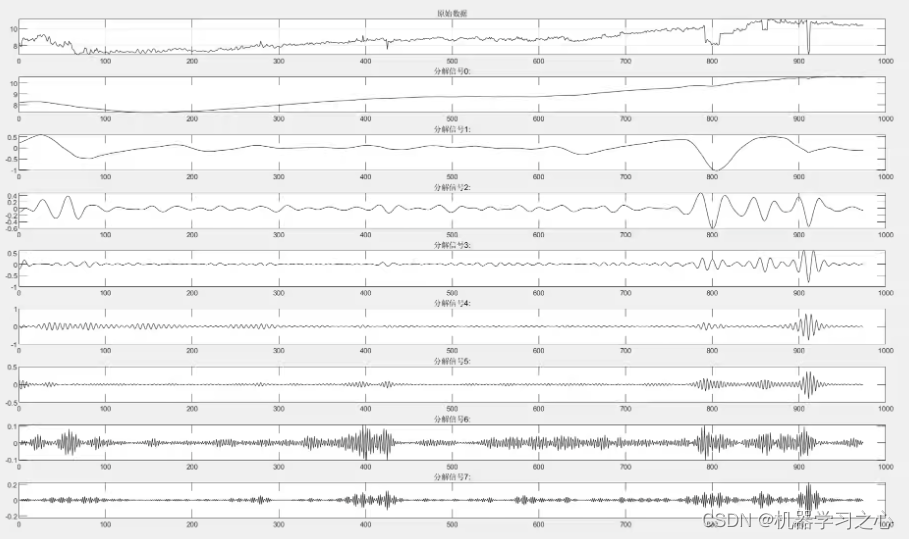
时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化
时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化 目录 时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 北方苍鹰优化算法NGO优化VMD,对其分解层数,惩罚因子数做优化…...
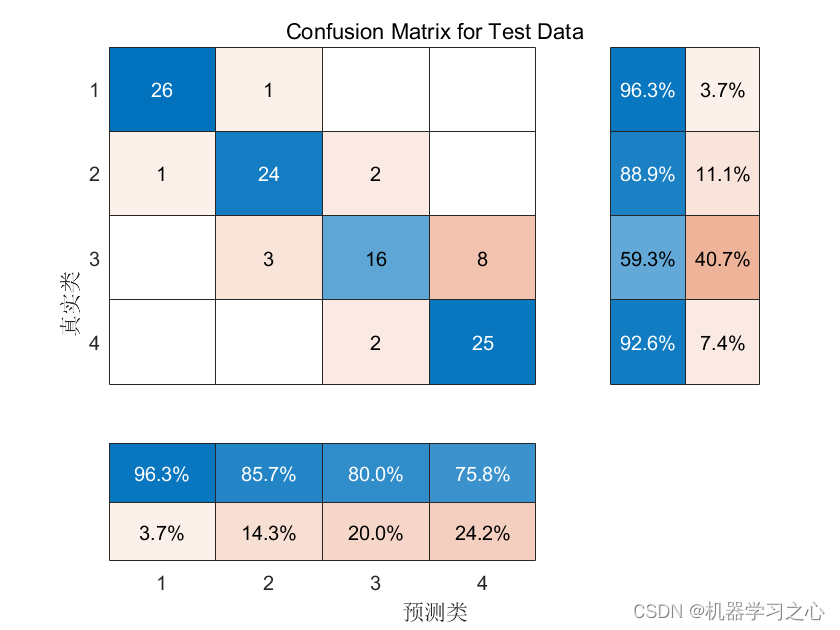
分类预测 | Matlab实现RBF-Adaboost多特征分类预测
分类预测 | Matlab实现RBF-Adaboost多特征分类预测 目录 分类预测 | Matlab实现RBF-Adaboost多特征分类预测效果一览基本介绍研究内容程序设计参考资料 效果一览 基本介绍 1.Matlab实现基于RBF-Adaboost数据分类预测(Matlab完整程序和数据) 2.多特征输入…...

【Java代码规范】阿里编码规约 VS CheckStyle
全文速览: 1、关于代码编码质量2、如何小成本有效管理企业内的编码规范 2.1 阿里编码规约IDE插件2.2 CheckStyle IDE插件 3、如何在代码提交中检验规范 3.1 阿里编码规约配置git precommit check3.2 CheckStyle配置git precommit check3.3 实践 1、关于代码编码质…...
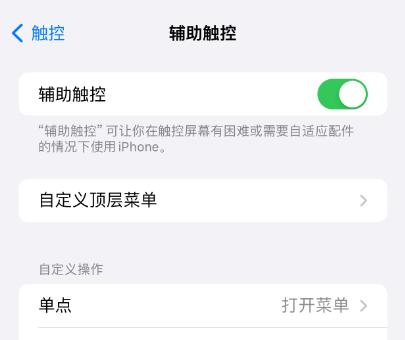
iPhone苹果15手机圆点怎么设置让屏幕上显示出来圆形图标?
iPhone苹果15手机圆点怎么设置让屏幕上显示出来圆形图标? 1、在iPhone苹果手机上找到「设置」并点击打开; 2、在苹果iPhone设置内找到「辅助功能」并点击打开; 3、在苹果iPhone手机辅助功能内的动作交互内找到「触控」并点击打开;…...

kibana报错内存溢出问题解决
一、背景: kibana内存溢出,进程被kill掉,导致前端页面访问不到。 报错内容 二、报错原因: 发现是前端 js 报的内存 oom 异常,通过网上资料发现node.js 的默认内存大小为1.4G Node 中通过 JavaScript 使用内存时只能…...

【C语法】1124循环结构
#include <stdio.h> int main(){ //输入一个数。倒叙输出各个位上的数。 //123456 6 5 4 3 2 1 // 1输出个位上的数 %10 // 2将这个数去掉个位上的数。 / 10 // 3当这个数最后变成0时结束 int a 0; printf("请输入一个正整数:"); scanf…...

在PHP8中向数组添加元素-PHP8知识详解
在php8中向数组添加元素有多种方法,在这里主要讲解几个常用的方法:使用方括号[]添加元素、使用array_unshift()函数,向数组的头部添加元素、使用array_push()函数,向数组的尾部添加元素、使用array_splice()函数添加元素。 1、使用…...
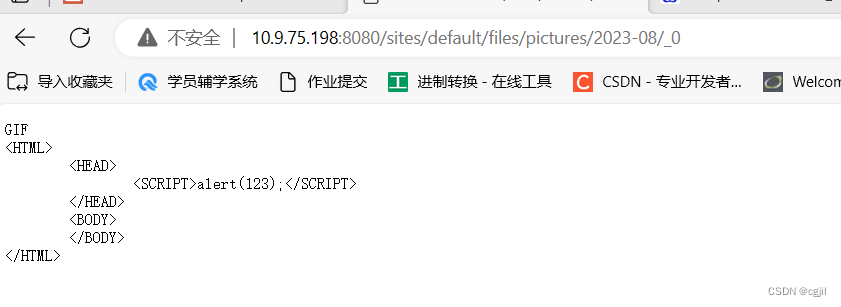
Drupal __ 8.5.0 __ XSS文件上传 __CVE-2019-6341
Drupal __ 8.5.0 __ XSS文件上传 __CVE-2019-6341 说明内容漏洞编号CVE-2019-6341漏洞名称Drupal XSS漏洞漏洞评级中危影响范围在7.65之前的Drupal 7版本中; 8.6.13之前的Drupal 8.6版本; 8.5.14之前的Drupal 8.5版本。漏洞描述Drupal诞生于2000年,是一…...
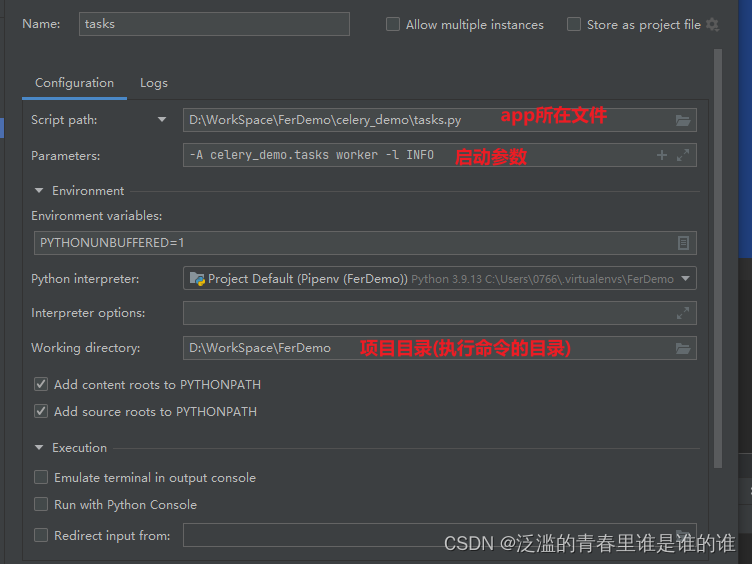
Pycharm中配置Celery启动
Pycharm中配置Celery启动 前置条件 目录结构 ----FerDemo --------celery_demo ------------tasks.py tasks.py文件代码 import sys import time from celery import Celeryapp Celery(demo,backendredis://:password127.0.0.1/0,brokerredis://:password127.0.0.1/1,broker…...

Jmeter —— 常用的几种断言方法(基本用法)
在使用JMeter进行性能测试或者接口自动化测试工作中,经常会用到的一个功能,就是断言,断言相当于检查点,它是用来判断系统返回的响应结果是否正确,以此帮我们判断测试是否通过,本文 主要介绍几种常用的断言&…...

mybatis bean属性识别丢失【NoSuchPropertyException】
背景 发现线上报错日志 org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.builder.BuilderException: Error evaluating expression Cause: org.apache.ibatis.ognl.NoSuchPropertyException: 参考 https://github.com/mybatis/mybatis-…...

点云从入门到精通技术详解100篇-基于补全点云与图像像素级融合的障碍物识别
目录 前言 感知融合技术研究现状及问题 感知融合技术概述 特征级融合研究现状...

商品分类显示scroll-view布局实现
快捷键 view{菜单数据$}*40 回车后即可快速生成 <view class="cates"> <!-- 搜索开始 --><SearchBar></SearchBar> <!-- 搜索结束 --> <view class="cates_container"> <!-- 左侧菜单 开始 --> <scroll-vie…...

基本的SELECT语句——“MySQL数据库”
各位CSDN的uu们好呀,好久没有更新小雅兰的MySQL数据库专栏啦,接下来一段时间,小雅兰都会更新MySQL数据库的知识,下面,让我们进入今天的主题吧——基本的SELECT语句!!! SQL概述 SQL语…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...
