线段树总结
文章目录
- 参考文档
- 题目
- 线段树实现
- 单点修改,区间求值
- 模板题目
- 308. 二维区域和检索 - 可变
- 区间修改,区间求值
- 1. 掉落的方块(区间开点)
- 2. 维护序列
- 3. 一个简单的问题2
- 4. 天际线问题
- 动态开点
- 1. 区间和个数(单点修改开点)
- 问题以及注意事项
参考文档
线段树动态开点java
动态开点c++
线段树leetcode题目
题目
| 题目 | 知识点/注意点 | 难度 |
|---|---|---|
| 更新数组后处理求和查询 | 线段树 | 困难 |
| 维护序列 | 区间修改、求和 | 困难 |
| 掉落的方块 | 右边区间-1 | 困难 |
| leetcode 气球颜色变换 | 右边区间-1 | |
| leetcode 218.天际线 | 右边区间-1 | 困难 |
| leetcode 307. 区域和检索 - 数组可修改 | 下标开始的位置 | 困难 |
| leetcode 315. 计算右侧小于当前元素的个数 | 保证r >= l | 困难 |
| leetcode 493. 翻转对 | 离散化 / 动态开点 | 困难 |
| leetcode 327. 区间和的个数 | 离散化 / 动态开点 | 困难 |
线段树实现
- 一般Push_down和push_up是需要手动实现的。
- 注意下标从1开始,build和使用的时候需要注意。
- 动态开点的时候,push_down和update会动态开点。
- 使用的时候,需要保证r >= l,否则会出现各种问题。
- 动态开点的时候,需要保证(l, r)的范围包含全部点。
单点修改,区间求值
模板题目
static const int maxn = 4e5 + 4;int sum[maxn];int n;void push_up(int u) {sum[u] = sum[u << 1] + sum[u << 1 | 1];}void build(int u, int l, int r, vector<int>&nums) {if (l == r) {sum[u] = nums[l - 1];return ;}int mid = (l + r) >> 1;build(u << 1, l, mid, nums);build(u << 1 | 1, mid + 1, r, nums);push_up(u);}void update(int u, int l, int r, int p, int x) {if (p == l && l == r) {sum[u] = x;return ;}int mid = (l + r) >> 1;if (p <= mid) update(u << 1, l, mid, p, x);else update(u << 1 | 1, mid + 1, r, p, x);push_up(u);}int query(int u, int l, int r, int L, int R) {if (L <= l && r <= R) {return sum[u];}int mid = (l + r) >> 1;int ans = 0;if (L <= mid) ans = query(u << 1, l, mid, L, R);if (R > mid) ans += query(u << 1 | 1, mid + 1, r, L, R);return ans; }
308. 二维区域和检索 - 可变
class Solution {
public:// 加是不行的。为什么呢?因为区间[l, r]上的高度不统一。static const int N = 1e6 + 10;int maxh[N], lc[N], rc[N], idx = 0, root = 0; // root应该写成全局变量,int lazy[N];// int add[N]; // 区间同时增加高度不行void push_up(int u) {maxh[u] = max(maxh[lc[u]], maxh[rc[u]]);}// 将区间,改编成add_h。如果没有区间就开点void push_down(int &u, int x) {if (!u) u = ++idx; // push_down的时候也需要创建新的lazy[u] = maxh[u] = x;}// 懒标记下推void push_down(int u) {// if (add[u] == 0) return ;if (lazy[u] == 0) return ;push_down(lc[u], lazy[u]);push_down(rc[u], lazy[u]);lazy[u] = 0; // 清除懒标记}// [L, R]增加add_x, 需要加上引用,让lc和rc指向正确位置。void update(int &u, int l, int r, int L, int R, int add_x) {if (u == 0) u = ++idx; // 给儿子创建一个新的点if (L <= l && r <= R) {push_down(u, add_x);// printf("add_x = %d\n", add_x);return ;}push_down(u);int mid = (l + r) >> 1;// printf("mid = %d l = %d r = %d, L = %d, R = %d\n", mid, l, r, L, R);if (L <= mid) update(lc[u], l, mid, L, R, add_x);if (R > mid) update(rc[u], mid + 1, r, L, R, add_x);push_up(u); // 没有传递u, 所以u不会变}// 询问,不用加引用int query(int u, int l, int r, int L, int R) {if (u == 0) return 0; // 如果没更新这个区间直接返回if (L <= l && r <= R) {return maxh[u];}push_down(u);int mid = (l + r) >> 1;int maxv = 0;// printf("%d %d %d %d %d\n", mid, l, r, L, R);if (L <= mid) maxv = query(lc[u], l, mid, L, R);if (R > mid) maxv = max(maxv, query(rc[u], mid + 1, r, L, R));return maxv;}vector<int> fallingSquares(vector<vector<int>>& positions) {vector<int>ans;for (auto vec : positions) {int l = vec[0], r = vec[0] + vec[1] - 1, z = vec[1];int cur = query(root, 1, 1e9, l, r);// printf("cur = %d\n", cur);update(root, 1, 1e9, l, r, z + cur);ans.push_back(maxh[1]);}return ans;}
};
区间修改,区间求值
1. 掉落的方块(区间开点)
大区间
少查询
动态开点: 使用指针的进行开点
离散化
int x = info[0], h = info[1], cur = query(1, 1, N, x, x + h - 1);
查询 – [x, x + h - 1]
修改 – [x, x + h - 1, cur + h]
当前的最大值就是tr[1].val
class Solution {
public:// 加是不行的。为什么呢?因为区间[l, r]上的高度不统一。static const int N = 1e6 + 10;int maxh[N], lc[N], rc[N], idx = 0, root = 0; // root应该写成全局变量,int lazy[N];// int add[N]; // 区间同时增加高度不行void push_up(int u) {maxh[u] = max(maxh[lc[u]], maxh[rc[u]]);}// 将区间,改编成add_h。如果没有区间就开点void push_down(int &u, int x) {if (!u) u = ++idx; // push_down的时候也需要创建新的lazy[u] = maxh[u] = x;}// 懒标记下推void push_down(int u) {// if (add[u] == 0) return ;if (lazy[u] == 0) return ;push_down(lc[u], lazy[u]);push_down(rc[u], lazy[u]);lazy[u] = 0; // 清除懒标记}// [L, R]增加add_xvoid update(int &u, int l, int r, int L, int R, int add_x) {if (u == 0) u = ++idx; // 给儿子创建一个新的点if (L <= l && r <= R) {push_down(u, add_x);// printf("add_x = %d\n", add_x);return ;}push_down(u);int mid = (l + r) >> 1;// printf("mid = %d l = %d r = %d, L = %d, R = %d\n", mid, l, r, L, R);if (L <= mid) update(lc[u], l, mid, L, R, add_x);if (R > mid) update(rc[u], mid + 1, r, L, R, add_x);push_up(u); // 没有传递u, 所以u不会变}int query(int &u, int l, int r, int L, int R) {if (u == 0) return 0; // 如果没更新这个区间直接返回if (L <= l && r <= R) {return maxh[u];}push_down(u);int mid = (l + r) >> 1;int maxv = 0;// printf("%d %d %d %d %d\n", mid, l, r, L, R);if (L <= mid) maxv = query(lc[u], l, mid, L, R);if (R > mid) maxv = max(maxv, query(rc[u], mid + 1, r, L, R));return maxv;}vector<int> fallingSquares(vector<vector<int>>& positions) {vector<int>ans;for (auto vec : positions) {int l = vec[0], r = vec[0] + vec[1] - 1, z = vec[1];int cur = query(root, 1, 1e9, l, r);// printf("cur = %d\n", cur);update(root, 1, 1e9, l, r, z + cur);ans.push_back(maxh[1]);}return ans;}
};
- 问题1:为什么动态开点不判断u是否为空?询问直接返回就行了,更新的时候需要判断。
- 问题2:直接把val赋值成为add,是否都是这样?还是仅仅是这个题目这样?仅仅这个题目这样。
2. 维护序列
调试技巧
- 首先判断build是否成功
- 其次判断询问是否成功
- 最后根据根节点的信息判断更新是否成功。
- push_down和push_up可以输出前后的sum[u]进行判断
3. 一个简单的问题2
java代码再acwnig的java代码上。
- long的使用
- 两个push_down
- 一个push_down是下推
- 另一个是更新区间的sum和懒标记
4. 天际线问题
class NumMatrix {
public:// 每一行使用一个线段树来维护static const int MAXN = 8e4 + 4;static const int N = 3e2 + 4;int sum[N][MAXN];vector<vector<int>>nums;int m, n;void push_up(int row, int u) {sum[row][u] = sum[row][u << 1] + sum[row][u << 1 | 1];}void build(int row, int u, int l, int r) {if (l == r) {sum[row][u] = nums[row][l - 1];return ;}int mid = (l + r) >> 1;// printf("%d %d %d\n", l, r, mid);build(row, u << 1, l, mid);build(row, u << 1 | 1, mid + 1, r);push_up(row, u);}void update(int u, int l, int r, int row, int col, int x) {if (l == r && col == l) { // l == r的时候col一定等于lsum[row][u] = x;return ;}int mid = (l + r) >> 1;if (col <= mid) update(u << 1, l, mid, row, col, x);else update(u << 1 | 1, mid + 1, r, row, col, x);push_up(row, u);}int query(int u, int l, int r, int row, int L, int R) {if (L <= l && r <= R) {return sum[row][u];}int mid = (l + r) >> 1;int ans = 0;if (L <= mid) ans += query(u << 1, l, mid, row, L, R);if (R > mid) ans += query(u << 1 | 1, mid + 1, r, row, L, R);return ans; }NumMatrix(vector<vector<int>>& matrix) {this->nums = matrix;m = nums.size();n = nums[0].size();for (int i = 0; i < m; i++) {build(i, 1, 1, n);// printf("%d\n", sum[i][1]);}}void update(int row, int col, int val) {col++;update(1, 1, n, row, col, val);}int sumRegion(int row1, int col1, int row2, int col2) {int ans = 0;col1++, col2++;for (int i = row1; i <= row2; i++) {ans += query(1, 1, n, i, col1, col2);}return ans;}
};/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix* obj = new NumMatrix(matrix);* obj->update(row,col,val);* int param_2 = obj->sumRegion(row1,col1,row2,col2);*/
动态开点
1. 区间和个数(单点修改开点)
- 注意求最大和最小值的过程
- 注意前缀和为0的情况需要加入进去。而前缀和为0的时候,不用考虑query,因为一定为0,所有的点都是0。
typedef long long LL;static const int N = 4e6 + 10; // 开太小了也爆栈LL add[N];int idx = 0, root = 0, lc[N], rc[N];void push_up(int u) {add[u] = add[lc[u]] + add[rc[u]]; // 如果使用node,可能会出现点不存在的情况,但是这里并不会,因为add[0] = 0;}// 单点修改开点void update(int &u, LL l, LL r, LL p) {if (!u) u = ++idx;// add[u]++; // 直接相当于push_up了if (l == r && l == p) {add[u] += 1;return ;} LL mid = (l + r) >> 1;if (p <= mid) update(lc[u], l, mid, p);else update(rc[u], mid + 1, r, p);push_up(u);}LL query(int u, LL l, LL r, LL L, LL R) {if (!u) return 0;if (L <= l && r <= R) return add[u];LL mid = (l + r) >> 1;LL ans = 0;if (L <= mid) ans += query(lc[u], l, mid, L, R);if (R > mid) ans += query(rc[u], mid + 1, r, L, R);return ans;}int countRangeSum(vector<int>& nums, int low, int high) {int n = nums.size();LL ans = 0;vector<LL>sum(n + 1);sum[0] = 0;memset(lc, 0, sizeof lc);memset(rc, 0 ,sizeof rc);for (int i = 1; i <= n; i++) {sum[i] = sum[i - 1] + nums[i - 1];}LL minv = LLONG_MAX, maxv = LLONG_MIN;for (LL x: sum) {minv = min({minv, x, x - high});maxv = max({maxv, x, x - high});}// cout << minv << " " << maxv << endl;for (LL x: sum) {LL l = x - high, r = x - low;// cout <<x << " " << l << " " << r << endl;ans += query(root, minv, maxv, l, r);// cout << query(root, minv, maxv, l, r) << endl;update(root, minv, maxv, x);}return ans;}
};
问题以及注意事项
- 天际线和方块的问题中,为什么需要右端点-1,而不是左端点 + 1呢?
- 具体的调试技巧,看上面的维护序列。
- 注意使用的时候,区间从1开始,
相关文章:

线段树总结
文章目录参考文档题目线段树实现单点修改,区间求值模板题目308. 二维区域和检索 - 可变区间修改,区间求值1. 掉落的方块(区间开点)2. 维护序列3. 一个简单的问题24. 天际线问题动态开点1. 区间和个数(单点修改开点)问题以及注意事…...
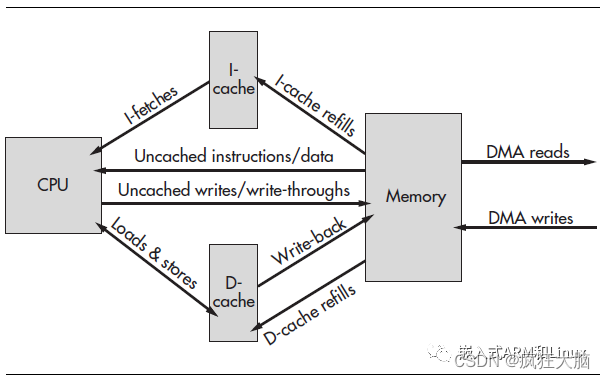
龙芯GS232(MIPS 32)架构cache管理笔记
1 mips32架构 MIPS架构是一种基于精简指令集(Reduced Instruction Set Computer,RISC)的计算机处理器架构。MIPS架构由MIPS Technologies公司在1981年开发,并在1984年发布了第一款MIPS处理器。 MIPS架构的特点包括: …...

js去重
<script>let arr [{ id: 0, name: "张三" },{ id: 1, name: "李四" },{ id: 2, name: "王五" },{ id: 3, name: "赵六" },{ id: 1, name: "孙七" },{ id: 2, name: "周八" },{ id: 2, name: "吴九&qu…...
小白都能看懂的C语言入门教程
文章目录C语言入门教程1. 第一个C语言程序HelloWorld2. C语言的数据类型3. 常量变量的使用4. 自定义标识符#define5. 枚举的使用6. 字符串和转义字符7. 判断和循环8. 函数9. 数组的使用10. 操作符的使用11. 结构体12. 指针的简单使用C语言入门教程 1. 第一个C语言程序HelloWor…...
leetcode 21~30 学习经历
leetcode 21~30 学习经历21. 合并两个有序链表22. 括号生成23. 合并K个升序链表24. 两两交换链表中的节点25. K 个一组翻转链表26. 删除有序数组中的重复项27. 移除元素28. 找出字符串中第一个匹配项的下标29. 两数相除30. 串联所有单词的子串小结21. 合并两个有序链表 将两个升…...

让ArcMap变得更加强大,用python执行地理处理以及编写自定义脚本工具箱
文章目录一、用python执行地理处理工具1.1 例:乘以0.00011.2 例:裁剪栅格1.3 哪里查看调用某工具的代码?二、用python批量执行地理处理工具2.1 必需的python语法知识for循环语句缩进的使用注释的使用2.2 一个批处理栅格的代码模板三、创建自定…...

SAP 项目实施阶段全过程
在sap实施项目的周期和步骤上,根据各公司对业务的理解不同,也被划分为各个阶段,但其中由普华永道提出的分七步走,个人觉得对刚进入这一行业的人很有帮助,接下来一起分享和讨论下: sap实施项目生命周期&…...

idea中的Maven导包失败问题解决总结
idea中的Maven导包失败问题解决总结 先确定idea和Maven 的配置文件settings 没有问题 找到我们本地的maven仓库,默认的maven仓库路径是在\C:\Users\用户名.m2下 有两个文件夹,repositotry是放具体jar包的,根据报错包的名,找对应文…...
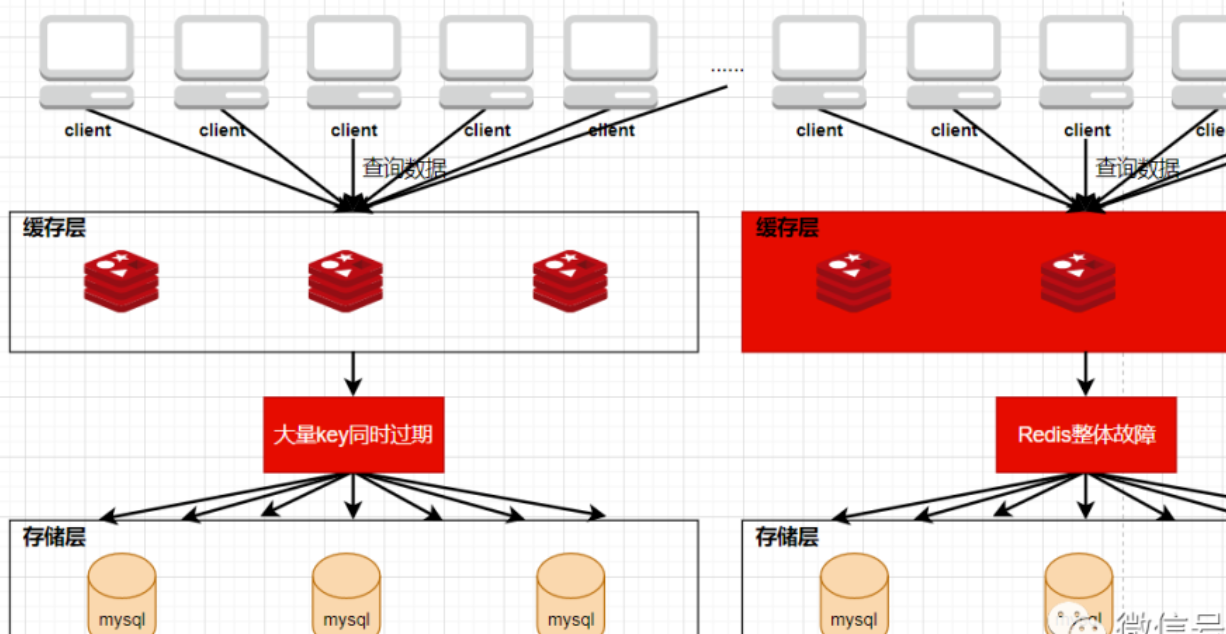
REDIS中的缓存穿透,缓存击穿,缓存雪崩原因以及解决方案
需求引入一般在项目的开发中,都是使用关系型数据库来进行数据的存储,通常不会存在什么高并发的情况,可是一旦涉及大数据量的需求,比如商品抢购,网页活动导致的主页访问量瞬间增大,单一使用关系型数据库来保存数据的系统…...
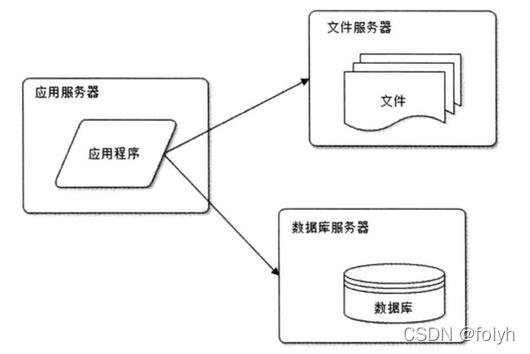
数据库及缓存之MySQL(一)
思维导图 常见知识点 1.mysql存储引擎: 2.innodb与myisam区别: 3.表设计字段选择: 4.mysql的varchar(M)最多存储数据: 5.事务基本特性: 6.事务并发引发问题: 7.mysql索引: 8.三星索引…...

项目管理中,项目经理需要具备哪些能力?
项目经理是团队的领导者,是带领项目团队对项目进行策划、执行,完成项目目标,对于项目经理来说,想要有序推进项目,使项目更成功,光有理论知识是不够的,也要具备这些能力: 1、分清主…...

itk中的一些图像处理
文章目录1.BinomialBlurImageFilter计算每个维度上的最近邻居平均值2.高斯平滑3.图像的高阶导数 RecursiveGaussianImageFilter4.均值滤波5.中值滤波6.离散高斯平滑7.曲率驱动流去噪图像 CurvatureFlowImageFilter8.由参数alpha和beta控制的幂律自适应直方图均衡化9.Canny 边缘…...
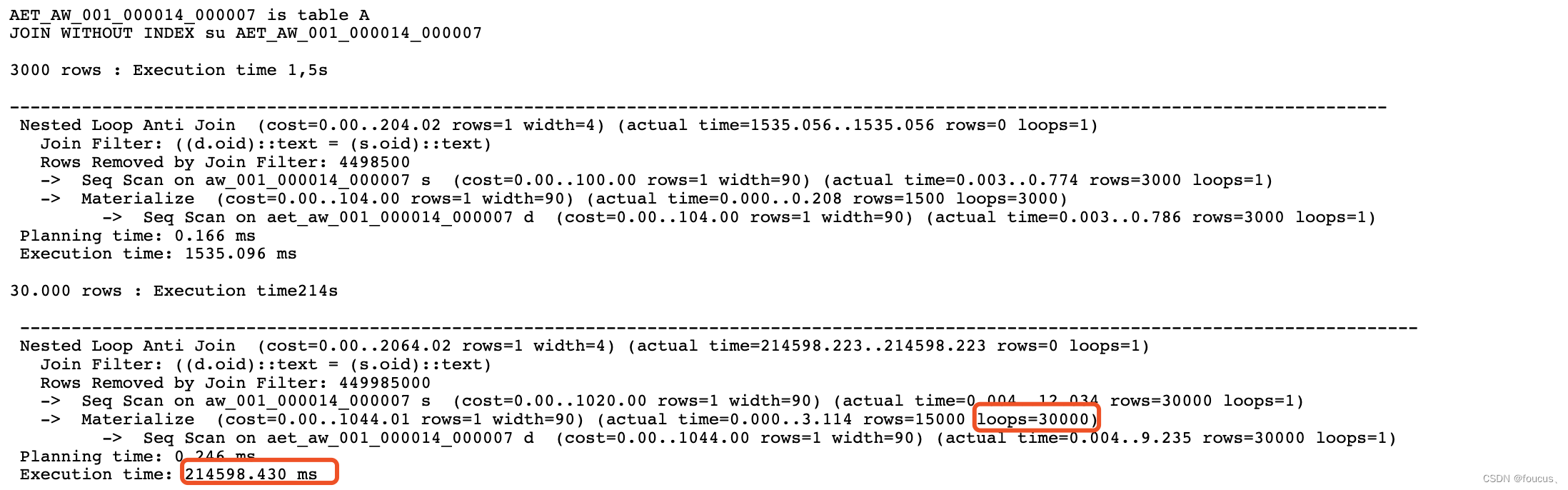
Endless lseek导致的SQL异常
最近碰到同事咨询的一个问题,在执行一个函数时,发现会一直卡在那里。 strace抓了下发现会话一直在执行lseek,大致情况如下: 16:13:55.451832 lseek(33, 0, SEEK_END) 1368064 <0.000037> 16:13:55.477216 lseek(33, 0, SE…...
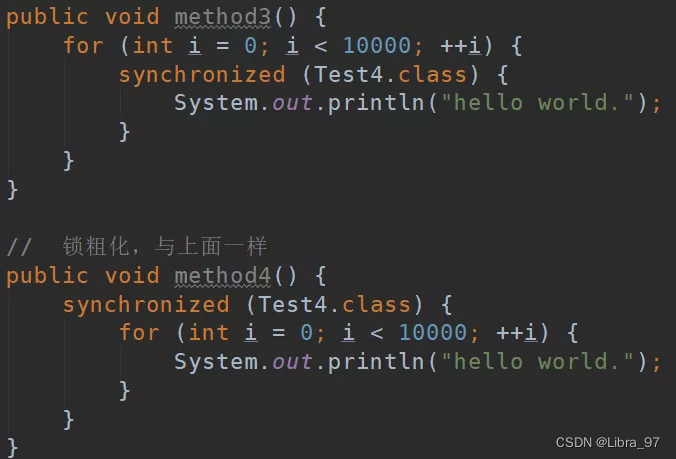
JUC-day01
JUC-day01 什么是JUC线程的状态: wait sleep关键字:同步锁 原理(重点)Lock接口: ReentrantLock(可重入锁)—>AQS CAS线程之间的通讯 1 什么是JUC 1.1 JUC简介 在Java中,线程部分是一个重点,本篇文章说的JUC也是关于线程的。JUC就是java.util .con…...
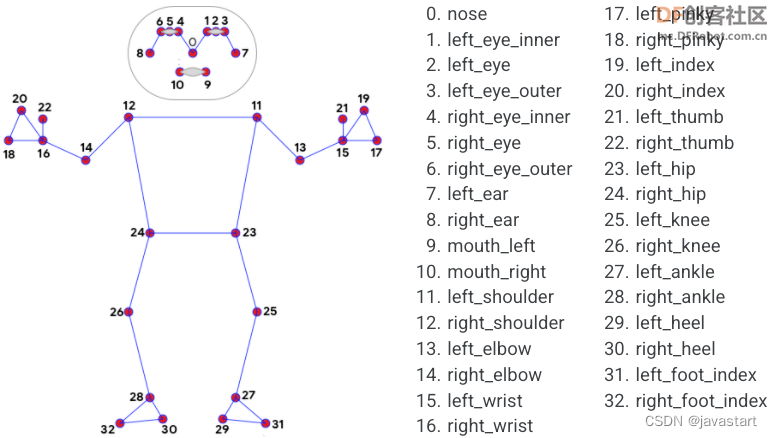
Mind+Python+Mediapipe项目——AI健身之跳绳
原文:MindPythonMediapipe项目——AI健身之跳绳 - DF创客社区 - 分享创造的喜悦 【项目背景】跳绳是一个很好的健身项目,为了获知所跳个数,有的跳绳上会有计数器。但这也只能跳完这后看到,能不能在跳的过程中就能看到,…...

数据库概述
20世纪60年代后期,就出现了数据库技术。取得成就如下:造就了四位图灵奖得主发展成为以数据建模和DBMS核心技术为主,内容丰富的一门学科。带动了一个巨大的软件产业-DBMS产品及其相关工具和解决方案。四个基本概念数据数据是数据库中存储的基本…...
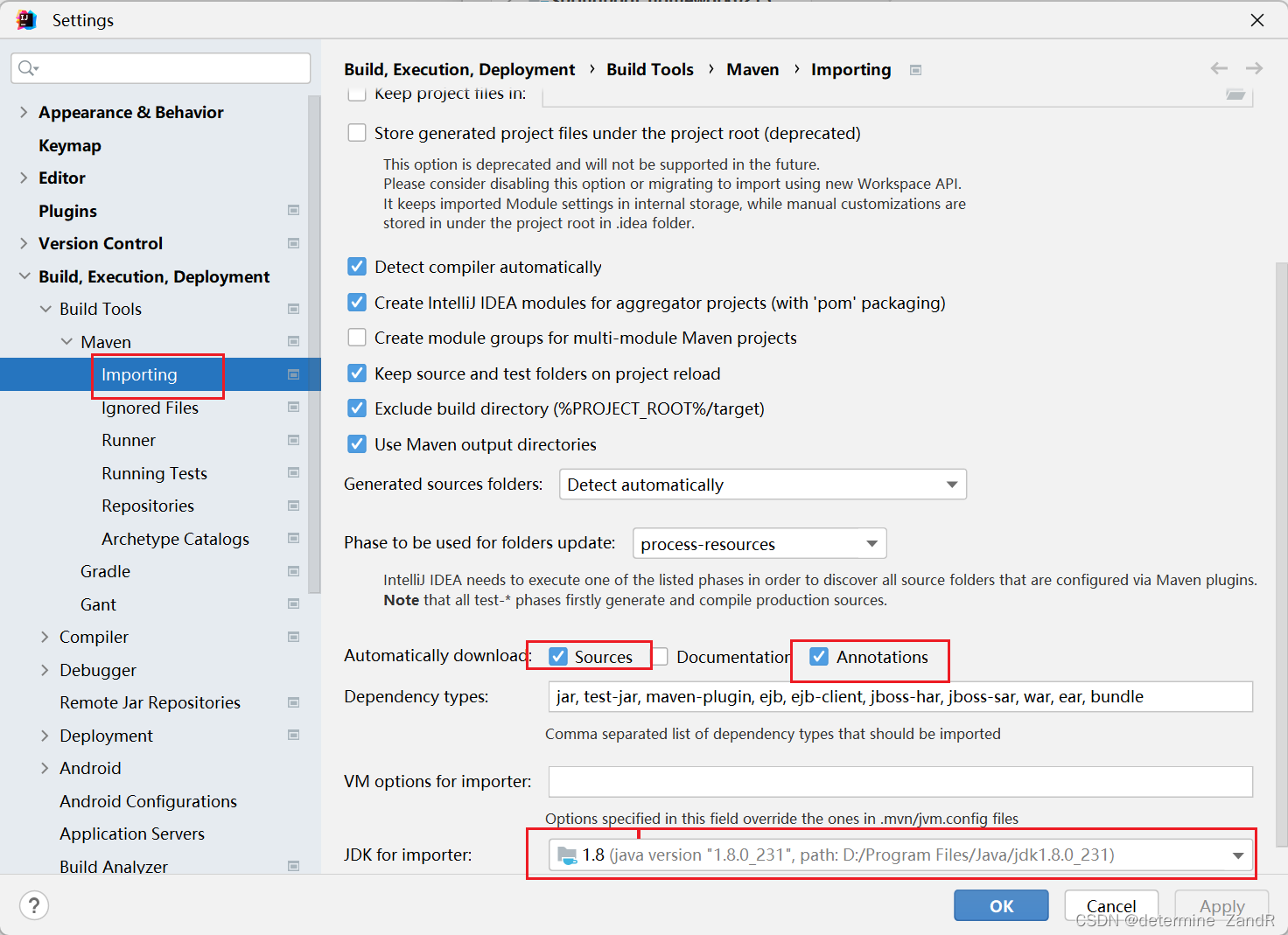
【已解决】解决IDEA的maven刷新依赖时出现Connot reconnect错误
前言 小编我将用CSDN记录软件开发求学之路上亲身所得与所学的心得与知识,有兴趣的小伙伴可以关注一下!也许一个人独行,可以走的很快,但是一群人结伴而行,才能走的更远!让我们在成长的道路上互相学习&#…...
文件的变编译和引用、执行)
动态链接库(.so)文件的变编译和引用、执行
动态链接库(.so)文件的变编译和引用 动态链接库:SO(Shared Object)是一种动态链接库,也被称为共享库。它是一种可被多个程序共享使用的二进制代码库,其中包含已编译的函数和代码。与静态链接库不同,动态链接…...
文件解压命令)
linux(centos8)文件解压命令
linux解压命令tar 解压命令常用解压命令1 [.tar] 文件 解压到当前文件夹2 [.tar.gz] 文件 解压到当前文件夹3 [.tar] 解压到指定文件夹 -C 必须是大写unzip 解压命令常用解压命令1 [.zip]解压到当前文件夹2 [.zip] 解压到指定文件夹2 [.zip] 解压到指定文件夹(强行覆…...

阅读笔记6——通道混洗
一、逐点卷积 当前先进的轻量化网络大都使用深度可分离卷积或组卷积,以降低网络的计算量,但这两种操作都无法改变特征图的通道数,因此需要使用11的卷积。总体来说,逐点的11卷积有如下两点特性: 可以促进通道之间的信息…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...

DriveGPT4: Interpretable End-to-end Autonomous Driving via Large Language Model
一、研究背景与创新点 (一)现有方法的局限性 当前智驾系统面临两大核心挑战:一是长尾问题,即系统在遇到新场景时可能失效,例如突发交通状况或非常规道路环境;二是可解释性问题,传统方法无法解释智驾系统的决策过程,用户难以理解车辆行为的依据。传统语言模型(如 BERT…...
)
Android多媒体——音/视频数据播放(十八)
在媒体数据完成解码并准备好之后,播放流程便进入了最终的呈现阶段。为了确保音视频内容能够顺利输出,系统需要首先对相应的播放设备进行初始化。只有在设备初始化成功后,才能真正开始音视频的同步渲染与播放。这一过程不仅影响播放的启动速度,也直接关系到播放的稳定性和用…...
