机器学习笔记之最优化理论与方法(八)无约束优化问题——常用求解方法(中)
机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[中]
- 引言
- 回顾:最速下降算法的缺陷
- 经典牛顿法基本介绍
- 经典牛顿法的问题
- 经典牛顿法的优点与缺陷
- 经典牛顿法示例
- 修正牛顿法介绍
- 拟牛顿法
- 拟牛顿法的算法过程
- 矩阵 B k + 1 \mathcal B_{k+1} Bk+1的获取方法
引言
本节将继续介绍无约束优化问题的常用求解方法,包括牛顿法、拟牛顿法。
本节是对优化算法(十八~二十)牛顿法的理论补充,其中可能出现一些定理的证明过程这里不再赘述,并在相应位置附加链接。
回顾:最速下降算法的缺陷
在上一节中介绍了最速下降法,并提到一个缺陷:梯度下降法仅使用负梯度方向作为下降方向。
- 不可否认的是:在每一次迭代过程中,负梯度方向必然是当前迭代步骤的最速下降方向,但它仅仅是局部最优解;
- 这个最速下降方向仅使用了目标函数 f ( ⋅ ) f(\cdot) f(⋅)在当前数值解 x k x_k xk的一阶梯度信息;而实际上二阶梯度信息同样可以参与下降方向的判别。
经典牛顿法基本介绍
相比之下,牛顿法 ( Newton Method ) (\text{Newton Method}) (Newton Method)则使用一阶与二阶梯度信息共同判别下降方向。从目标函数的角度观察,可以理解为:对 x k x_k xk处的二次逼近函数进行最小化。
使用泰勒展开式对目标函数 f ( x ) f(x) f(x)进行二阶泰勒展开:
对于经典牛顿法 ( Pure Newton Method ) (\text{Pure Newton Method}) (Pure Newton Method),仅设置步长α k = 1 \alpha_k=1 αk=1。与最速下降法相反,在牛顿法中我们更关注迭代过程中选择的方向,而非步长。其中x − x k x - x_k x−xk表示下降方向;
min f ( x ) = min f [ x k + 1 ⋅ ( x − x k ) ] = min { f ( x k ) + 1 1 ! ⋅ [ ∇ f ( x k ) ] T ( x − x k ) + 1 2 ! ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) + O ( ∥ x − x k ∥ 2 ) } ≈ min { f ( x k ) + 1 1 ! ⋅ [ ∇ f ( x k ) ] T ( x − x k ) + 1 2 ! ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) } \begin{aligned} \min f(x) & = \min f[x_k + 1\cdot (x - x_k)] \\ & = \min \left\{ f(x_k) + \frac{1}{1!} \cdot [\nabla f(x_k)]^T(x - x_k) + \frac{1}{2!} (x - x_k)^T \nabla^2 f(x_k) (x -x_k) + \mathcal O(\|x - x_k\|^2)\right\} \\ & \approx \min \left\{ f(x_k) + \frac{1}{1!} \cdot [\nabla f(x_k)]^T(x - x_k) + \frac{1}{2!} (x - x_k)^T \nabla^2 f(x_k) (x -x_k)\right\} \end{aligned} minf(x)=minf[xk+1⋅(x−xk)]=min{f(xk)+1!1⋅[∇f(xk)]T(x−xk)+2!1(x−xk)T∇2f(xk)(x−xk)+O(∥x−xk∥2)}≈min{f(xk)+1!1⋅[∇f(xk)]T(x−xk)+2!1(x−xk)T∇2f(xk)(x−xk)}
从而直接对上述二元函数求解最小值。首先求解梯度 ∇ f ( x ) \nabla f(x) ∇f(x):
∇ f ( x ) = ∇ f ( x k ) + 1 2 ⋅ [ ∇ 2 f ( x k ) ] T ⋅ 2 ( x − x k ) \nabla f(x) = \nabla f(x_k) + \frac{1}{2} \cdot [\nabla^2 f(x_k)]^T \cdot2(x - x_k) ∇f(x)=∇f(xk)+21⋅[∇2f(xk)]T⋅2(x−xk)
令 ∇ f ( x ) ≜ 0 \nabla f(x) \triangleq 0 ∇f(x)≜0,有:
{ [ ∇ 2 f ( x k ) ] T ( x − x k ) = − ∇ f ( x k ) ⇒ x = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) \begin{cases} [\nabla^2 f(x_k)]^T (x - x_k) = -\nabla f(x_k) \\ \Rightarrow x = x_k - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k) \end{cases} {[∇2f(xk)]T(x−xk)=−∇f(xk)⇒x=xk−[∇2f(xk)]−1∇f(xk)
很明显,该线搜索表达方式中: α k = 1 , D k = − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) \alpha_k = 1,\mathcal D_k = -[\nabla^2 f(x_k)]^{-1} \nabla f(x_k) αk=1,Dk=−[∇2f(xk)]−1∇f(xk)。其对应算法迭代步骤这里不再赘述,见牛顿法与正则化一节。
经典牛顿法的问题
观察上述迭代公式: x = x k − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) x = x_k - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k) x=xk−[∇2f(xk)]−1∇f(xk)
- 如果该迭代公式能够正常执行,必然需要满足 ∇ 2 f ( x k ) ≻ 0 \nabla^2 f(x_k) \succ 0 ∇2f(xk)≻0,即 x k x_k xk位置对应的 Hessian Matrix \text{Hessian Matrix} Hessian Matrix必然是正定矩阵。由 ∇ 2 f ( x k ) ≻ 0 \nabla^2 f(x_k) \succ 0 ∇2f(xk)≻0可以推出:二次逼近函数 f ( x ) = f ( x k ) + [ ∇ f ( x k ) ] T ( x − x k ) + 1 2 ( x − x k ) T ∇ 2 f ( x k ) ( x − x k ) \begin{aligned}f(x) = f(x_k) + [\nabla f(x_k)]^T (x - x_k) + \frac{1}{2}(x -x_k)^T \nabla^2 f(x_k)(x - x_k)\end{aligned} f(x)=f(xk)+[∇f(xk)]T(x−xk)+21(x−xk)T∇2f(xk)(x−xk)必然是凸函数,从而 D k = − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) \mathcal D_k = -[\nabla^2 f(x_k)]^{-1} \nabla f(x_k) Dk=−[∇2f(xk)]−1∇f(xk)是下降方向,并且是全局最优解。
这里可以解决优化算法(十八)经典牛顿法中的疑惑。并不是所有情况下f ( x ) f(x) f(x)是凸函数,开口向上有最小解;只有∇ 2 f ( x k ) ≻ 0 \nabla^2 f(x_k) \succ 0 ∇2f(xk)≻0时才可以。 - 相反,如果 Hessian Matrix ⇒ ∇ 2 f ( x k ) \text{Hessian Matrix } \Rightarrow \nabla^2 f(x_k) Hessian Matrix ⇒∇2f(xk)不是正定矩阵:
- 如果存在 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)特征值为 0 0 0—— [ ∇ 2 f ( x k ) ] − 1 [\nabla^2 f(x_k)]^{-1} [∇2f(xk)]−1无法求解;
- 如果存在 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)特征值为负值——那么观察 [ ∇ f ( x k ) ] T D k [\nabla f(x_k)]^{T} \mathcal D_k [∇f(xk)]TDk:
在上一节介绍了[ ∇ f ( x k ) ] T D k [\nabla f(x_k)]^T \mathcal D_k [∇f(xk)]TDk的物理意义:x k x_k xk所在位置关于方向向量 D k \mathcal D_k Dk的方向导数;当[ ∇ f ( x k ) ] T D k < 0 [\nabla f(x_k)]^T \mathcal D_k < 0 [∇f(xk)]TDk<0时,方向向量D k \mathcal D_k Dk是下降方向。
[ ∇ f ( x k ) ] T D k = − [ ∇ f ( x k ) ] T [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) [\nabla f(x_k)]^T \mathcal D_k = - [\nabla f(x_k)]^T [\nabla^2 f(x_k)]^{-1}\nabla f(x_k) [∇f(xk)]TDk=−[∇f(xk)]T[∇2f(xk)]−1∇f(xk)
很明显,该结果是三个矩阵的线性组合,如果 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)中存在一个负特征值,加上开始的负号,其连加项中必然存在一个结果是正值,虽然不清楚该正值的具体大小,但能够肯定的是: [ ∇ f ( x k ) ] T D k [\nabla f(x_k)]^T\mathcal D_k [∇f(xk)]TDk不能百分之百地确认其小于 0 0 0,从而 D k \mathcal D_k Dk未必是下降方向。
经典牛顿法的优点与缺陷
- 优点:
- 当初始点 x 0 x_0 x0足够接近于收敛点 x ∗ x^* x∗时,并且 ∇ 2 f ( x ) \nabla^2 f(x) ∇2f(x)满足较好性质时,其收敛速度是二阶收敛。
相关证明详见优化算法(十九)经典牛顿法的收敛性分析,这里不再赘述。 - 该方法具有二次终止性。
如果使用牛顿法求解凸二次函数最小化问题时,不仅存在二次终止性,甚至可以实现一步终止。因为求得的下降方向是全局最优方向。
- 当初始点 x 0 x_0 x0足够接近于收敛点 x ∗ x^* x∗时,并且 ∇ 2 f ( x ) \nabla^2 f(x) ∇2f(x)满足较好性质时,其收敛速度是二阶收敛。
- 缺陷:
- 首先,在迭代过程中只有更新位置的 Hessian Matrix ⇒ ∇ 2 f ( ⋅ ) ≻ 0 \text{Hessian Matrix } \Rightarrow \nabla^2 f(\cdot) \succ 0 Hessian Matrix ⇒∇2f(⋅)≻0时才能使用;
- 并且由于 Hessian Matrix \text{Hessian Matrix} Hessian Matrix是 n n n阶方阵,其计算时间复杂度是 O ( k 3 ) \mathcal O(k^3) O(k3),计算量大。并且适用范围较窄。
经典牛顿法示例
这里依然使用最速下降法中的示例:最小化目标函数 min f ( x , y ) = 1 2 x 2 + 2 y 2 \begin{aligned}\min f(x,y) = \frac{1}{2}x^2 + 2y^2\end{aligned} minf(x,y)=21x2+2y2,设置初始点 x 0 = ( 2 1 ) T x_0 = (2 \quad 1)^T x0=(21)T对于凸二次函数的解法可以实现一步收敛。对应代码表示如下:
import numpy as np
import math
import matplotlib.pyplot as pltdef f(x, y):return 0.5 * (x ** 2) + 2 * (y ** 2)def Derf(x,y):return np.array([x,4 * y])def DoubleDerf():return np.array([[1.0,0.0],[0.0,4.0]])def ConTourFunction(x,Contour):return math.sqrt(0.5 * (Contour - (0.5 * (x ** 2))))def NewtomMethod(epsilon=0.001):Start = np.array([2.0,1.0])LocList = list()LocList.append(Start)alpha = 0.2NextList = list()while True:D = np.linalg.inv(DoubleDerf()).dot(Derf(Start[0],Start[1]))Next = Start - alpha * DNextList.append(Next)if np.linalg.norm(Derf(Next[0],Next[1])) <= epsilon:LocList.append(Next)breakelse:Start = NextLocList.append(NextList[-1])return LocListdef DrawPicture(LocList):ContourList = [0.1,0.2,0.5,1.0]LimitParameter = 0.0001plt.figure(figsize=(10, 5))for Contour in ContourList:# 设置范围时,需要满足x的定义域描述。x = np.linspace(-1 * math.sqrt(2 * Contour) + LimitParameter, math.sqrt(2 * Contour) - LimitParameter, 200)y1 = [ConTourFunction(i, Contour) for i in x]y2 = [-1 * j for j in y1]plt.plot(x, y1, '--', c="tab:blue")plt.plot(x, y2, '--', c="tab:blue")plotList = list()for (x, y) in LocList:plotList.append((x, y))plt.scatter(x, y, s=50, facecolor="none", edgecolors="tab:red", marker='o')if len(plotList) < 2:continueelse:plt.plot([plotList[0][0], plotList[1][0]], [plotList[0][1], plotList[1][1]], c="tab:red")plotList.pop(0)plt.show()if __name__ == '__main__':LocList = NewtomMethod()DrawPicture(LocList)
当alpha=1.0时,对应图像结果表示如下:
可以看出,选择准确的方向与合适的步长,即可达到一步收敛。

当然,如果给出的步长过小,导致收敛可能无法一步到位。例如:alpha=0.2时的图像结果表示如下:
在该示例中,由于目标函数是凸二次函数,因而它的二阶逼近函数就是目标函数自身。从而每次寻找的方向都是全局最优方向。

修正牛顿法介绍
针对经典牛顿法中的缺陷:
{ D k = − [ ∇ 2 f ( x k ) ] − 1 ∇ f ( x k ) α k = 1 \begin{cases} \mathcal D_k = - [\nabla^2 f(x_k)]^{-1} \nabla f(x_k) \\ \alpha_k = 1 \end{cases} {Dk=−[∇2f(xk)]−1∇f(xk)αk=1
针对步长 α k \alpha_k αk的修正:
-
修正原因:牛顿法是对目标函数的二阶逼近函数进行优化。而不是真正对目标函数自身进行优化。如果目标函数过于复杂,其对应泰勒展开式中高阶项系数无法忽视,这导致:仅仅表示成二阶逼近函数无法对目标函数进行充分表示。
反之,如果仅使用二阶逼近函数表示复杂函数,会导致:虽然默认的 α k = 1 \alpha_k=1 αk=1能够使二阶逼近函数有效收敛,但可能无法使目标函数有效收敛。
-
修正方法:由于方向必然是下降方向,那么基于该方向使用线搜索方法(如 Wolfe \text{Wolfe} Wolfe准则)重新确定 α k \alpha_k αk。
针对方向 D k \mathcal D_k Dk的修正:
- 方法一:正则化法。如果 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)不是正定矩阵,使用矩阵 B k \mathcal B_k Bk进行替代: D k = − B k − 1 ∇ f ( x k ) \mathcal D_k = -\mathcal B_k^{-1} \nabla f(x_k) Dk=−Bk−1∇f(xk)。
关于正则化法的详细介绍见本节内链接牛顿法与正则化。
B k = ∇ 2 f ( x k ) + λ I \mathcal B_k = \nabla^2 f(x_k) + \lambda \mathcal I Bk=∇2f(xk)+λI
其中 I \mathcal I I表示单位矩阵; λ \lambda λ为适当正数为保持 B k \mathcal B_k Bk正定。
这也称作Hessian Matrix \text{Hessian Matrix} Hessian Matrix主对角线扰动; - 方法二:正则化法的优化版:
关于方法一的缺陷:λ \lambda λ的取值存在约束/技巧。假设∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)不是正定矩阵,并且其对应的特征值为λ i ( i = 1 , 2 , ⋯ , n ) \lambda_i(i=1,2,\cdots,n) λi(i=1,2,⋯,n),对应λ \lambda λ的取值必须满足:
λ > max i = 1 , 2 , ⋯ , n { − λ i } \lambda > \mathop{\max}\limits_{i=1,2,\cdots,n} \{-\lambda_i\} λ>i=1,2,⋯,nmax{−λi}
这意味着:满足该条件的 λ \lambda λ值可能会很大,并且是每一个对角线元素加上 λ \lambda λ。从而导致原始特征值被λ \lambda λ被分掉相应权重。
优化版:可以将 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)进行特征值分解
其中Diag ( τ i ) \text{Diag}(\tau_i) Diag(τi)表示由特征值τ i \tau_i τi构成的对角阵。
∇ 2 f ( x k ) = Q T Diag ( τ i ) Q \nabla^2 f(x_k) = \mathcal Q^T \text{Diag}(\tau_i) \mathcal Q ∇2f(xk)=QTDiag(τi)Q
对于 τ i ( i = 1 , 2 , ⋯ , n ) \tau_i(i=1,2,\cdots,n) τi(i=1,2,⋯,n)可以执行如下操作:
其中δ \delta δ是一适当的正数。
τ i = { τ i if τ i ≥ δ δ Otherwise \tau_i = \begin{cases} \tau_i \quad \text{if } \tau_i \geq \delta \\ \delta \quad \text{Otherwise} \end{cases} τi={τiif τi≥δδOtherwise
这种操作相比于方法一的优势在于:关于 > 0 >0 >0的特征值,没有修改它的特征信息,从而该维度依然受到 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)自身特征值的主导。 - 方法三:若存在某一步骤其 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)不是正定矩阵,可以在该步骤中直接使用最速下降法替代牛顿法。我们不否认:
最速下降法的方向可能不优秀(局部最优),但它至少必然是下降方向。
拟牛顿法
拟牛顿法 ( Quasi-Newton Method ) (\text{Quasi-Newton Method}) (Quasi-Newton Method)与牛顿法相似,其都是考虑:目标函数 f ( ⋅ ) f(\cdot) f(⋅)在 x k x_k xk位置的二阶逼近函数。记该函数为 m k ( x ) m_k(x) mk(x),表示如下:
m k ( x ) = f ( x k ) + [ ∇ f ( x k ) ] T ( x − x k ) + 1 2 ( x − x k ) T B k ( x − x k ) B k ≻ 0 m_k(x) = f(x_k) + [\nabla f(x_k)]^T(x - x_k) + \frac{1}{2} (x - x_k)^T\mathcal B_k(x - x_k) \quad \mathcal B_k \succ 0 mk(x)=f(xk)+[∇f(xk)]T(x−xk)+21(x−xk)TBk(x−xk)Bk≻0
但拟牛顿法与牛顿法的核心区别在于:牛顿法使用 Hessian Matrix ⇒ ∇ 2 f ( x k ) \text{Hessian Matrix} \Rightarrow \nabla^2 f(x_k) Hessian Matrix⇒∇2f(xk)作为二次型位置的矩阵:
- 其中 ∇ 2 f ( x k ) ∈ R n × n \nabla^2 f(x_k) \in \mathbb R^{n \times n} ∇2f(xk)∈Rn×n,不容易计算;
- ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)性质不够稳定,它可能是一个非正定矩阵。
而拟牛顿法则直接使用正定矩阵 B k ≻ 0 \mathcal B_k \succ 0 Bk≻0替代 ∇ 2 f ( x k ) \nabla^2 f(x_k) ∇2f(xk)。当然 B k \mathcal B_k Bk仅仅是一个正定矩阵虽然在计算上便捷了,但我们同样期望它能存在如下性质:
- B k \mathcal B_k Bk能够体现 m k ( x ) m_k(x) mk(x)的一些二阶梯度信息;
- 相比于 ∇ 2 f ( x k ) ∈ R n × n \nabla^2 f(x_k) \in\mathbb R^{n \times n} ∇2f(xk)∈Rn×n的不易获取,期望 B k \mathcal B_k Bk相比之下能够更容易获取。
后续操作与牛顿法别无二致:
{ ∇ m k ( x ) = ∇ f ( x k ) + B k ( x − x k ) = 0 ⇒ x = x k − B k − 1 ∇ f ( x k ) \begin{cases} \nabla m_k(x) = \nabla f(x_k) + \mathcal B_k (x - x_k) = 0 \\ \quad \\ \Rightarrow x = x_k- \mathcal B_k^{-1} \nabla f(x_k) \end{cases} ⎩ ⎨ ⎧∇mk(x)=∇f(xk)+Bk(x−xk)=0⇒x=xk−Bk−1∇f(xk)
并记 D k = − B k − 1 ∇ f ( x k ) \mathcal D_k = - \mathcal B_k^{-1}\nabla f(x_k) Dk=−Bk−1∇f(xk)为使 min m k ( x ) \min m_k(x) minmk(x)的下降方向。
其对应的方向导数: [ ∇ f ( x k ) ] T D k < 0 [\nabla f(x_k)]^T \mathcal D_k < 0 [∇f(xk)]TDk<0恒成立。
拟牛顿法的算法过程
关于拟牛顿法的算法过程表示如下:
- 初始化:初始点 x 0 x_0 x0;描述终止条件的 ϵ \epsilon ϵ; k = 0 k=0 k=0;以及初始状态下的正定矩阵 B 0 \mathcal B_0 B0:
我们既希望B 0 \mathcal B_0 B0包含该函数在x 0 x_0 x0点处的二阶梯度信息,又希望该B 0 \mathcal B_0 B0是稳定的正定矩阵。例如根据上述方法,以∇ 2 f ( x 0 ) \nabla^2 f(x_0) ∇2f(x0)为基础,并对该矩阵进行修正。
B 0 = ∇ 2 f ( x 0 ) + λ ⋅ I B 0 ≻ 0 \mathcal B_0 = \nabla^2 f(x_0) + \lambda \cdot \mathcal I \quad \mathcal B_0 \succ 0 B0=∇2f(x0)+λ⋅IB0≻0 - 判断当前点 x k x_k xk是否为收敛点: if ∥ ∇ f ( x k ) ∥ ≤ ϵ \text {if } \|\nabla f(x_k)\| \leq \epsilon if ∥∇f(xk)∥≤ϵ,如果是,算法终止;反之,向下执行步骤;
- 计算下降方向: D k = − B k − 1 ∇ f ( x k ) \mathcal D_k = - \mathcal B_k^{-1} \nabla f(x_k) Dk=−Bk−1∇f(xk)
- 基于下降方向,通过非线性搜索方法(例如 Armijo , Wolfe \text{Armijo},\text{Wolfe} Armijo,Wolfe)来确定步长 α k \alpha_k αk;
- 计算下一个更新点 x k + 1 x_{k+1} xk+1的位置: x k + 1 = x k + α k ⋅ D k x_{k+1} = x_k + \alpha_k \cdot \mathcal D_k xk+1=xk+αk⋅Dk;并确定 x k + 1 x_{k+1} xk+1对应的 B k + 1 \mathcal B_{k+1} Bk+1。返回步骤 2 2 2,如果满足条件,算法停止;反之,继续迭代。
核心问题很明显: B k + 1 \mathcal B_{k+1} Bk+1怎么求 ? ? ?只要 B k + 1 \mathcal B_{k+1} Bk+1求出来,就可以得到相应的下降方向,从而持续迭代过程。
其中 B k + 1 \mathcal B_{k+1} Bk+1的确定方式有很多种,从而对应不同的拟牛顿法。
矩阵 B k + 1 \mathcal B_{k+1} Bk+1的获取方法
获取矩阵 B k + 1 \mathcal B_{k+1} Bk+1的基本要求
关于矩阵 B k + 1 \mathcal B_{k+1} Bk+1,它的基本要求是:
该方程也被称作拟牛顿方程。
∇ f ( x k + 1 ) − ∇ f ( x k ) = B k + 1 ( x k + 1 − x k ) \nabla f(x_{k+1}) - \nabla f(x_k) = \mathcal B_{k+1} (x_{k+1} - x_k) ∇f(xk+1)−∇f(xk)=Bk+1(xk+1−xk)
为什么 B k + 1 \mathcal B_{k+1} Bk+1需要满足该条件 ? ? ?
-
根据上述算法流程,完全可以确定 x k + 1 x_{k+1} xk+1的具体位置,从而可以计算出目标函数 f ( ⋅ ) f(\cdot) f(⋅)在该位置处的梯度信息: ∇ f ( x k + 1 ) \nabla f(x_{k+1}) ∇f(xk+1);
如果是正常牛顿法,我们需要继续计算Hessian Matrix ⇒ ∇ 2 f ( x k + 1 ) \text{Hessian Matrix } \Rightarrow \nabla^2 f(x_{k+1}) Hessian Matrix ⇒∇2f(xk+1)用于下一次迭代。 -
并且 ∇ f ( x k ) \nabla f(x_k) ∇f(xk)是上一次迭代位置 x k x_k xk的梯度结果,是已知项。观察上述等式左侧,根据拉格朗日中值定理,可以表示为如下形式:
由于没有办法确定x k , x k + 1 x_k,x_{k+1} xk,xk+1之间的大小关系,因而关于ξ \xi ξ的描述表示为:ξ = λ ⋅ x k + ( 1 − λ ) ⋅ x k + 1 ; λ ∈ ( 0 , 1 ) \xi = \lambda \cdot x_k + (1 - \lambda) \cdot x_{k+1};\lambda \in (0,1) ξ=λ⋅xk+(1−λ)⋅xk+1;λ∈(0,1)而不是ξ ∈ ( x k , x k + 1 ) \xi \in (x_k,x_{k+1}) ξ∈(xk,xk+1)
∇ f ( x k + 1 ) − ∇ f ( x k ) = ∇ 2 f ( ξ ) ⋅ ( x k + 1 − x k ) \nabla f(x_{k+1}) - \nabla f(x_k) = \nabla^2 f(\xi) \cdot (x_{k+1} - x_k) ∇f(xk+1)−∇f(xk)=∇2f(ξ)⋅(xk+1−xk) -
对比拉格朗日中值定理与拟牛顿方程,相当于使用 B k + 1 \mathcal B_{k+1} Bk+1对 ∇ 2 f ( ξ ) \nabla^2 f(\xi) ∇2f(ξ)进行替换,并且拟牛顿方程内,除了 B k + 1 \mathcal B_{k+1} Bk+1,其余项均是已知项。所以 B k + 1 \mathcal B_{k+1} Bk+1可求。
继续观察:关于矩阵 [ B k + 1 ] n × n [\mathcal B_{k+1}]_{n \times n} [Bk+1]n×n,首先它必然是对称矩阵,从而包含 n ( n + 1 ) 2 \begin{aligned}\frac{n(n+1)}{2}\end{aligned} 2n(n+1)个变量(
上三角/下三角阵元素数量);但拟牛顿方程所描述的方程组内仅包含 n n n个方程( x k , x k + 1 ∈ R n x_k,x_{k+1}\in \mathbb R^n xk,xk+1∈Rn),由于 n ( n + 1 ) 2 ≥ n ; n ∈ N + \begin{aligned}\frac{n(n+1)}{2} \geq n;n \in \mathbb N^{+}\end{aligned} 2n(n+1)≥n;n∈N+恒成立,从而满足拟牛顿方程的 B k + 1 \mathcal B_{k+1} Bk+1不唯一。 -
为表达方便,记:
它们都是拟牛顿方程~
{ y k = B k + 1 S k S k = H k + 1 y k ⇐ { y k = ∇ f ( x k + 1 ) − ∇ f ( x k ) S k = x k + 1 − x k H k = B k − 1 \begin{cases} y_k = \mathcal B_{k+1} \mathcal S_k \\ \mathcal S_k = \mathcal H_{k+1} y_k \end{cases} \Leftarrow \begin{cases} y_k = \nabla f(x_{k+1}) - \nabla f(x_k) \\ \mathcal S_k = x_{k+1} - x_k \\ \mathcal H_k = \mathcal B_k^{-1} \end{cases} {yk=Bk+1SkSk=Hk+1yk⇐⎩ ⎨ ⎧yk=∇f(xk+1)−∇f(xk)Sk=xk+1−xkHk=Bk−1
矩阵 B k + 1 \mathcal B_{k+1} Bk+1的选择
选择 B k + 1 \mathcal B_{k+1} Bk+1的核心思路:通过已有信息 ( y k , S k , B k ) ⇒ B k + 1 (y_k,\mathcal S_k,\mathcal B_k) \Rightarrow \mathcal B_{k+1} (yk,Sk,Bk)⇒Bk+1或者已有信息 ( y k , S k , H k ) ⇒ H k + 1 (y_k,\mathcal S_k,\mathcal H_k) \Rightarrow \mathcal H_{k+1} (yk,Sk,Hk)⇒Hk+1。
求出那个都可以,因为最终我们需要获取下降方向: D k + 1 = − B k + 1 − 1 ∇ f ( x k + 1 ) = − H k + 1 ∇ f ( x k + 1 ) \mathcal D_{k+1} = - \mathcal B_{k+1}^{-1} \nabla f(x_{k+1}) = -\mathcal H_{k+1} \nabla f(x_{k+1}) Dk+1=−Bk+1−1∇f(xk+1)=−Hk+1∇f(xk+1)
-
方法一:找到满足拟牛顿方程并且与 B k \mathcal B_k Bk相似的正定矩阵 B \mathcal B B作为 B k + 1 \mathcal B_{k+1} Bk+1。其数学符号表示如下:
这里通过对矩阵差异性求解范数来表示近似关系,关于近似关系的表示不唯一。
B k + 1 ⇒ B : { min ∥ B − B k ∥ s.t. B S k = y k ; B T = B \mathcal B_{k+1} \Rightarrow \mathcal B:\begin{cases} \min \|\mathcal B - \mathcal B_k\| \\ \text{s.t. } \mathcal B \mathcal S_k = y_k;\mathcal B^T = \mathcal B \end{cases} Bk+1⇒B:{min∥B−Bk∥s.t. BSk=yk;BT=B
同样可以通过上述思想选择矩阵 H \mathcal H H:
H k + 1 ⇒ H : { min ∥ H − H k ∥ s.t. H y k = S k ; H T = H \mathcal H_{k+1} \Rightarrow \mathcal H:\begin{cases} \min \|\mathcal H - \mathcal H_k\| \\ \text{s.t. } \mathcal H y_k = \mathcal S_k;\mathcal H^T = \mathcal H \end{cases} Hk+1⇒H:{min∥H−Hk∥s.t. Hyk=Sk;HT=H -
方法二:其思想是: B k + 1 / H k + 1 \mathcal B_{k+1}/\mathcal H_{k+1} Bk+1/Hk+1是基于 B k / H k \mathcal B_k/\mathcal H_k Bk/Hk的校正(优化)结果。令 B k + 1 = B k + Δ B \mathcal B_{k+1} = \mathcal B_k + \Delta \mathcal B Bk+1=Bk+ΔB:
无论是Rank-1 \text{Rank-1} Rank-1还是Rank-2 \text{Rank-2} Rank-2校正,其朴素思想是迭代过程中,避免关于 B k + 1 \mathcal B_{k+1} Bk+1的复杂运算。同理,关于H k + 1 \mathcal H_{k+1} Hk+1也可以使用H k + 1 = H k + Δ H \mathcal H_{k+1} = \mathcal H_k + \Delta \mathcal H Hk+1=Hk+ΔH进行描述。- Rank-1 \text{Rank-1} Rank-1校正:要求 Δ B \Delta \mathcal B ΔB的秩为 1 1 1。代表方法有: SR-1 \text{SR-1} SR-1方法。
- Rank-2 \text{Rank-2} Rank-2校正: 要求 Δ B \Delta \mathcal B ΔB的秩为 2 2 2。代表方法有: DFP \text{DFP} DFP方法, BFGS \text{BFGS} BFGS方法。
下一节将具体介绍 DFP \text{DFP} DFP以及 BFGS \text{BFGS} BFGS方法。
Reference \text{Reference} Reference:
最优化理论与方法-第六讲-无约束优化问题(二)
相关文章:

机器学习笔记之最优化理论与方法(八)无约束优化问题——常用求解方法(中)
机器学习笔记之最优化理论与方法——基于无约束优化问题的常用求解方法[中] 引言回顾:最速下降算法的缺陷经典牛顿法基本介绍经典牛顿法的问题经典牛顿法的优点与缺陷经典牛顿法示例 修正牛顿法介绍拟牛顿法拟牛顿法的算法过程 矩阵 B k 1 \mathcal B_{k1} Bk1的…...

Django系列:Django简介与MTV架构体系概述
Django系列 Django简介与MTV架构体系概述 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/132890054 【介…...

锐捷交换机WEB管理系统EXCU_SHELL密码信息泄漏漏洞
一、漏洞简介 锐捷交换机 WEB 管理系统 EXCU_SHELL存在密码信息泄露漏洞,攻击者可从漏洞获取到管理员账号密码,从而以管理员权限登录。 二、影响版本 锐捷交换机 WEB 管理系统 三、资产测绘 hunterweb.body"img/free_login_ge.gif"&&…...

线性代数(六) 线性变换
前言 《线性空间》定义了空间,这章节来研究空间与空间的关联性 函数 函数是一个规则或映射,将一个集合中的每个元素(称为自变量)映射到另一个集合中的唯一元素(称为因变量)。 一般函数从 “A” 的每个元…...

Python基础运算分享
Python的运算符和其他语言类似 (我们暂时只了解这些运算符的基本用法,方便我们展开后面的内容,高级应用暂时不介绍) 数学运算 >>>print 19 # 加法>>>print 1.3-4 # 减法>>>print 3*5 …...
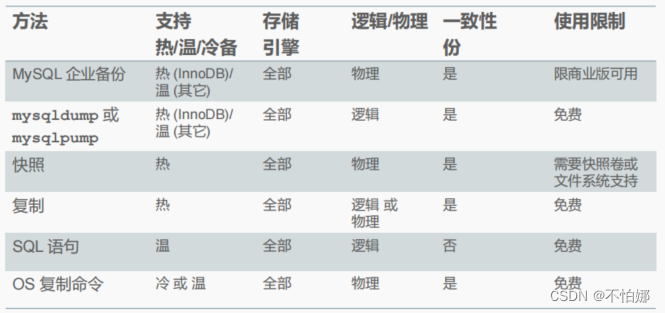
【MySQL】mysql中有哪几种类型的备份技术?它们各自有什么优缺点?
为什么要备份?备份类型(从类型的角度)备份技术(从技术手段的角度)不同备份方法的比较感谢 💖 为什么要备份? 数据库或它所在的平台可能会出现问题,这时候数据库中的数据可能就遭到了…...

5基于pytorch的多目标粒子群算法,MOPSO,引导种群逼近真实Pareto前沿,算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。
基于pytorch的多目标粒子群算法,MOPSO,引导种群逼近真实Pareto前沿,算法运行结束后将外部存档中粒子作为获得的Pareto最优解近似。程序已调通,可以直接运行。 5pytorch多目标粒子群算法最优解5pytorch多目标粒子群算法最优解 (xiaohongshu.co…...

002 Linux 权限
前言 本文将会向您介绍关于linux权限方面的内容,包括文件类型,如何切换用户、基本权限、粘滞位等等 Linux具体的用户 超级用户:可以再linux系统下做任何事情,不受限制 普通用户:在linux下做有限的事情。 超级用户的…...

【Java 基础篇】Java可变参数:灵活处理不定数量的方法参数
在Java编程中,可变参数是一项强大的功能,它允许你编写更加灵活的方法,接受不定数量的参数。本文将详细解释Java可变参数的用法、语法以及最佳实践。 什么是可变参数? 可变参数是Java 5引入的一项功能,它允许你在方法…...

“网站建设流程详解:从概念到上线的每个细节“
以下是网站建设流程的详细步骤,从概念到上线的每个细节: 确定网站目标和定位:明确网站的主题和目标,根据目标受众和市场定位来决定网站的内容和设计风格。考虑网站的目的、目标受众、行业或领域等方面,以及网站的定位…...

DC/DC开关电源学习笔记(七)低压大电流DC/DC变换技术
低压大电流DC/DC变换技术 1. 无暂态要求的低压大电流DC/DC变换技术2. 负载极其快速变化的低压大电流DC/DC变换技术2.1 非隔离型 VRM2.2 隔离型VRM低压大电流高功率 DC/DC 变换技术,已从前些年的 3.3V 降至现在的 1.0V 左右,电流目前已可达到几十安至几百安。同时,电源的输出指标…...

XUbuntu22.04之查找进程号pidof、pgrep总结(一百九十)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

BI与数据治理以及数据仓库有什么区别
你可能已经听说过BI、数据治理和数据仓库这些术语,它们在现代企业中起着重要的作用。虽然它们都与数据相关,但它们之间有着明显的区别和各自独特的功能。数聚将详细探讨BI(商业智能)、数据治理和数据仓库之间的区别,帮…...

java---jar详解
一、help C:\Users\lichf1>jar 用法: jar {ctxui}[vfmn0PMe] [jar-file] [manifest-file] [entry-point] [-C dir] files ... 选项:-c 创建新档案-t 列出档案目录-x 从档案中提取指定的 (或所有) 文件-u 更新现有档案-v 在标准输出中生成详细输出-f 指定档案文件名-m…...
uni-app 新增 微信小程序之新版隐私协议
一、manifest.json中配置 "__usePrivacyCheck__": true 二、编写封装后的组件 <template><view class"privacy" v-if"showPrivacy"><view class"content"><view class"title">隐私保护指引</…...
nbcio-boot移植到若依ruoyi-nbcio平台里一formdesigner部分(四)
到目前为止,虽然基础的formdesigner部分已经完成,但流程用formdesigner提交与审批过程中的显示还有问题。 1、后端部分 其中FormConf修改如下: package com.ruoyi.flowable.core;import lombok.Data;import java.util.List; import java.uti…...

公交查询系统
目录 需求分析 1 概述 2 课题分析 3 实现功能步骤 4 项目背景 概要设计 1 系统流程图. 2 功能模块. 3 各功能模块 4 数据存储 5 类设计 三、详细设计 1公交线路查询系统用户界面 2公交信息存储模快 3公交信息查询模块 4用户信息输入和输出模块 四、调试分析 五、使用说明 六、…...

opencv 轮廓顶点重新排序----四边形
def reorder(myPoints):# print(myPoints.shape)# 创建一个与myPoints具有相同形状和类型的数组myPointsNew np.zeros_like(myPoints)# 数组重塑为一个4行2列的数组myPoints myPoints.reshape((4,2))# 计算myPoints数组中每一行(即每个点)的坐标和add …...

【项目实战】【已开源】USB2.0 HUB 集线器的制作教程(详细步骤以及电路图解释)
写在前面 本文是一篇关于 USB2.0 HUB 集线器的制作教程,包括详细的步骤以及电路图解释。 本文记录了笔者制作 USB2.0 HUB 集线器的心路历程,希望对你有帮助。 本文以笔记形式呈现,通过搜集互联网多方资料写成,非盈利性质…...
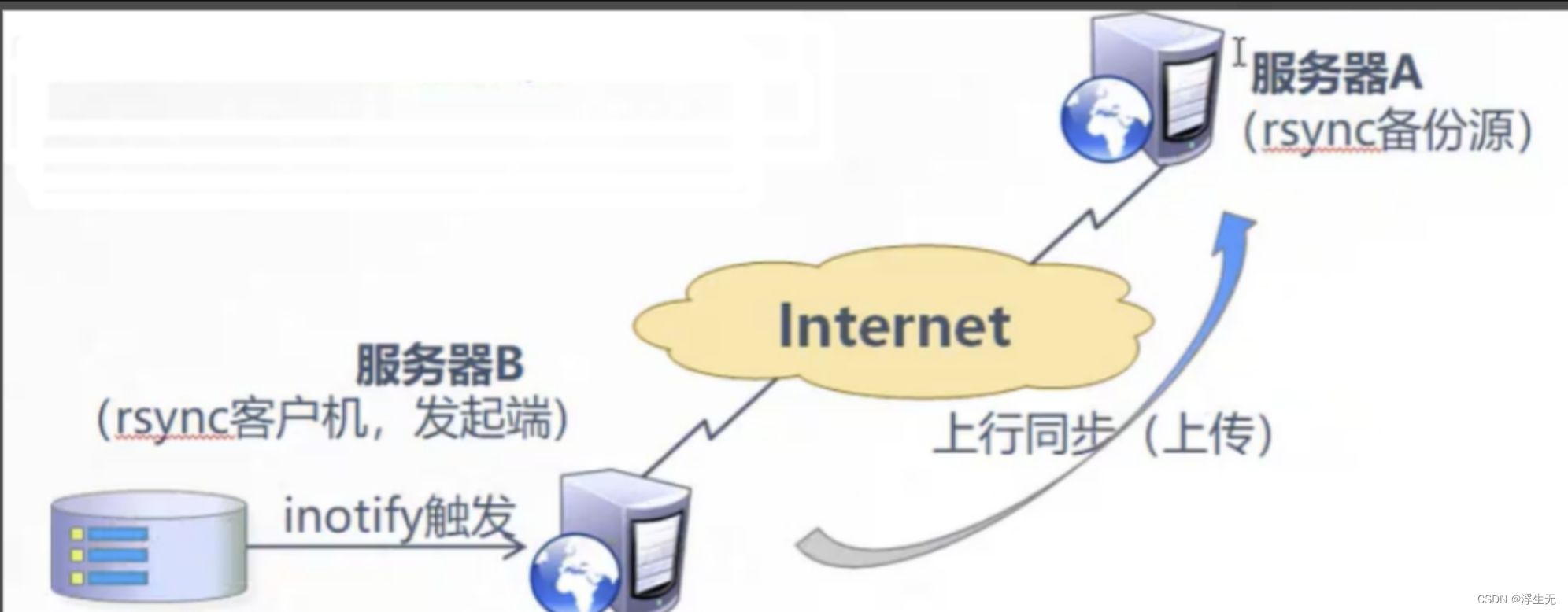
分布式运用之rsync远程同步
一、rsync的相关知识 1.1 rsync简介 rsync(Remote Sync,远程同步)是一个开源的快速备份工具,可以在不同主机之间镜像同步整个目录树,支持增量备份,并保持链接和权限,且采用优化的同步算法&am…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
