算法总结10 线段树
算法总结10 线段树
- 线段树
- 2569. 更新数组后处理求和查询
线段树
有一个数组,我们要:
- 更新数组的值(例如:都加上一个数,把子数组内的元素取反)
- 查询一个子数组的值(例如:求和,求最大值,求最小值)
更新于查询,如果暴力去做,每个操作都是O(n)的。所以我们需要提升效率。
两大思想:
- 挑选O(n)个特殊区间,使得任意一个区间,可以拆分为O(logn)个特殊区间(用最近公共祖先来思考)
O(n)<=4n
挑选O(n)个特殊区间:build
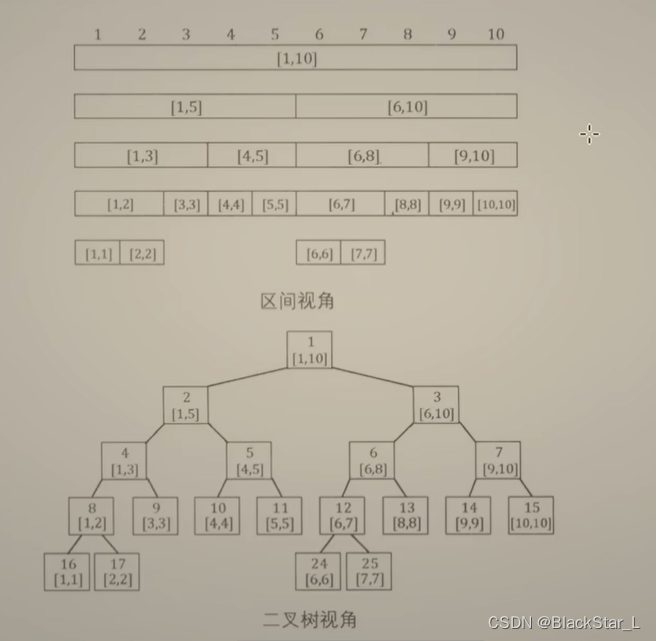
- lazy 更新 / 延迟更新
lazy tag:用一个数组维护每个区间需要更新的值
如果说这个值 = 0,表示不需要更新
如果这个值 != 0,表示更新操作在这个区间停住了,不继续地柜更新子区间了
如果后面又来了一个更新,破坏了于lazy tag的区间,那么这个区间就得继续递归更新了
模板:
class Solution:def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:n = len(nums1)todo = [0] * (4 * n)def build(o: int, l: int, r: int) -> None:if l == r:# ...returnm = (l + r) // 2build(o * 2, l, m)build(o * 2 + 1, m + 1, r)# 维护...# 更新 [L,R]def update(o: int, l: int, r: int, L: int, R: int, add: int) -> None:if L <= l and r <= R:# 更新 ...todo[o] += add # 不再继续递归更新了return m = (l + r)//2# 需要继续递归,就把 todo[o] 的内容传下去(给左右儿子)if todo[o] != 0:todo[o*2] += todo[o]todo[o*2+1] += todo[o]todo[o] = 0if m >= L:update(o*2, l, m, L, R, add)if m < R:update(o*2+1, m+1, r, L, R, add)# 维护 ...
2569. 更新数组后处理求和查询
2569. 更新数组后处理求和查询
class Solution:def handleQuery(self, nums1: List[int], nums2: List[int], queries: List[List[int]]) -> List[int]:n = len(nums1)cnt = [0]*(4*n)todo = [False]*(4*n)# 求非叶子节点def maintain(o):cnt[o] = cnt[o*2] + cnt[o*2+1]# 进行01翻转def do(o, l, r):# 翻转cnt[o] = r-l+1-cnt[o]# 翻一次为反,翻两次为正todo[o] = not todo[o]# 初始化线段树def build(o, l, r):# 叶子结点if l == r:cnt[o] = nums1[l-1]return# 非叶子结点 mid = (l+r)//2build(o*2, l, mid)build(o*2+1, mid+1, r)maintain(o)def update(o, l, r, L, R):if L<=l and r<=R:do(o, l, r)returnmid = (l+r)//2# 先将当前节点的值传给子节点if todo[o]:do(o*2, l, mid)do(o*2+1, mid+1, r)todo[o]=False# 待翻转的区间有分歧,二分处理if mid>=L:update(o*2, l, mid, L, R)if mid<R:update(o*2+1,mid+1, r, L, R)# 反转后更新节点的值maintain(o)# 初始化build(1, 1, n)# 记录答案,求和(每次都是在sum(nums2)的基础上增加值l*cnt[1])ans, s = [], sum(nums2)for op, l, r in queries:if op == 1:# 每次都从整个范围,将l+1和r+1的范围进行翻转(索引从1开始)update(1, 1, n, l+1, r+1)elif op == 2:# cnt从1开始s += l*cnt[1]else:ans.append(s)return ans参考
相关文章:

算法总结10 线段树
算法总结10 线段树 线段树2569. 更新数组后处理求和查询 线段树 有一个数组,我们要: 更新数组的值(例如:都加上一个数,把子数组内的元素取反)查询一个子数组的值(例如:求和&#x…...

518抽奖软件,支持按人像照片抽奖
518抽奖软件简介 518抽奖软件,518我要发,超好用的年会抽奖软件,简约设计风格。 包含文字号码抽奖、照片抽奖两种模式,支持姓名抽奖、号码抽奖、数字抽奖、照片抽奖。(www.518cj.net) 照片抽奖模式 圆角边框 照片抽奖模式下&am…...
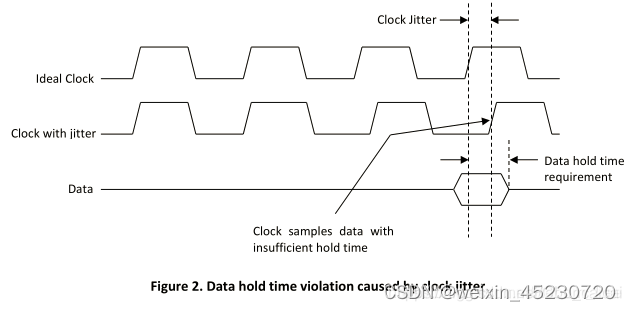
数字IC笔试面试题之--时钟偏斜(skew)与抖动(jitter)
1 时钟偏斜(clock skew) 时钟偏斜(偏移)是因为布线长度和负载不同,导致同一时钟上升沿到不同触发器的时间不同。这一时间差,即为时钟偏移。 时钟偏斜可能导致时序违例(本文直接粘贴了参考博客…...

免费api接口:物流api,企业工商查询api,游戏api。。。
免费api接口,物流api,企业工商查询api,游戏api。。。都有。 Facebook Games Services - Facebook Games Services 为游戏开发者提供了各种服务, 包括(但不限于) 成就 API, 分数 API, 应用通知, 请求, 游戏养成和 Facebook SDK for Unity.Google Play Games Service…...

第二十八章 Classes - 引用其他类的方法
文章目录 第二十八章 Classes - 引用其他类的方法引用其他类的方法对当前实例的引用 第二十八章 Classes - 引用其他类的方法 引用其他类的方法 在方法(或例程)中,使用下面的语法来引用其他类中的方法: 要调用类方法并访问其返回值,请使用如下表达式:…...
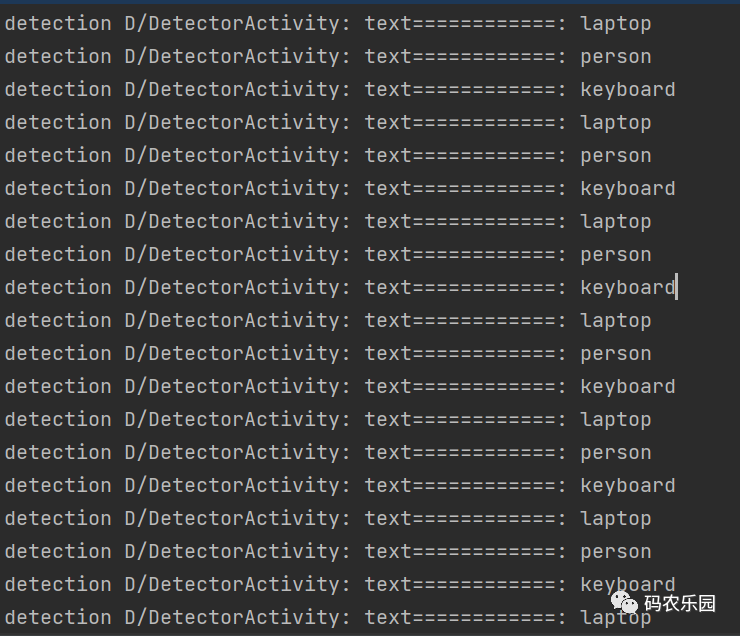
Android 中集成 TensorFlow Lite图片识别
在上图通过手机的相机拍摄到的物体识别出具体的名称,这个需要通过TensorFlow 训练的模型引用到项目中;以下就是详细地集成 TensorFlow步骤,请按照以下步骤进行操作: 在项目的根目录下的 build.gradle 文件中添加 TensorFlow 的 Ma…...
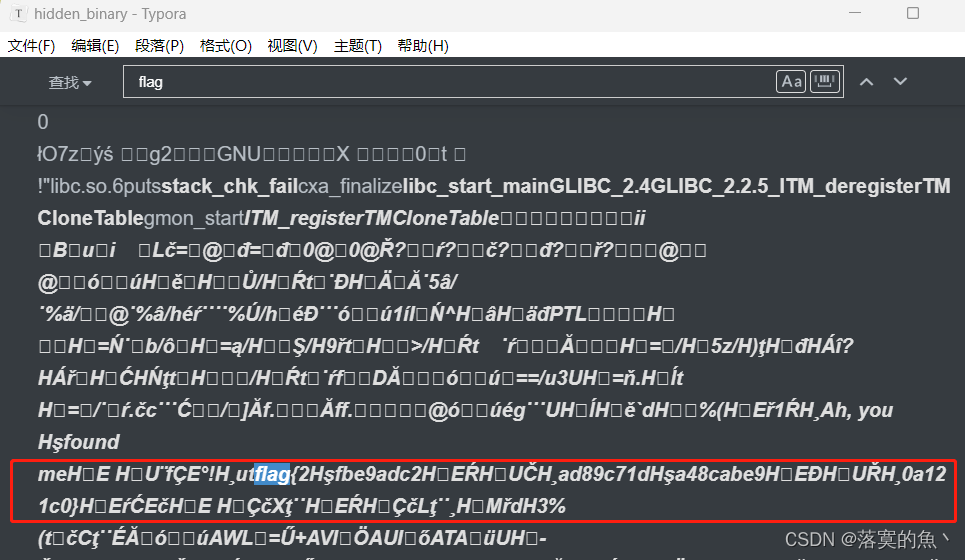
NSSCTF之Misc篇刷题记录(16)
NSSCTF之Misc篇刷题记录(16) [黑盾杯 2020]encrypt[UTCTF 2020]Spectre[UTCTF 2020]Observe closely NSSCTF平台:https://www.nssctf.cn/ PS:所有FLAG改为NSSCTF [黑盾杯 2020]encrypt UTAxSlUwTkRWRVo3Um1GclpWOWxibU55ZVhCMGFX…...

域名解析--nslookup和dig
dig (Domain Information Groper) dig 是一个功能强大且更灵活的 DNS 查询工具,通常在 Linux 和 macOS 等 Unix-like 操作系统上使用。以下是 dig 的一些常见用法和区别: 查询域名信息 dig example.com这将返回与指定域名相关的 DNS 记录,…...
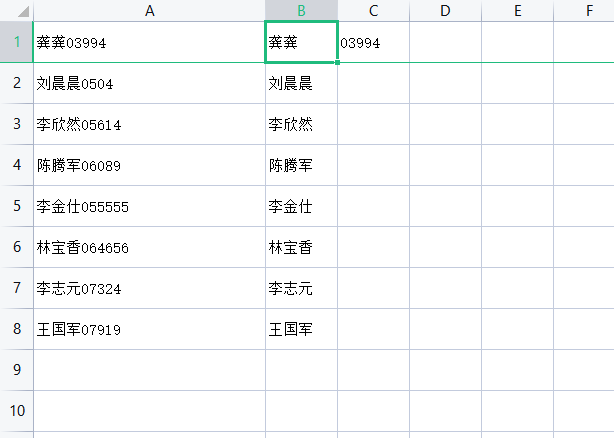
EXCEL如何把一个单元格内的文本和数字分开?例如:龚龚15565 = 龚龚 15565
使用工具:WPS 举例: EXCEL如何把一个单元格内的文本和数字批量分开?不使用数据分列。 第一步、将第二行数据冻结 第二步、在B1、C1单元格输入需要分开的示例 第三步、点击选中B1单元格,输入快捷键【CTRLE】进行填充。B2单元格也是…...
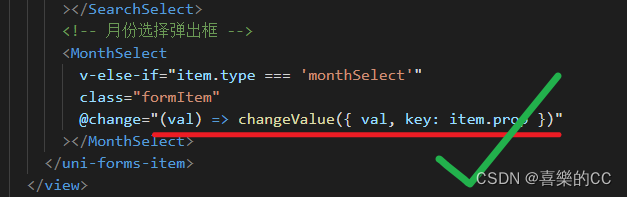
uniapp抽取组件绑定事件中箭头函数含花括号无法解析
版本: "dcloudio/uni-ui": "^1.4.27", "vue": "> 2.6.14 < 2.7"... 箭头函数后含有花括号的时候, getData就拿不到val参数 , 解决办法就是去除花括号 // 错误代码: <SearchComp change"(val) > { getData({ val …...

猫头虎博主第四期赠书活动:《精通Go语言:(第2版) 》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

【学习总结】EasyExcel合并同列不同行,表格数据相同的行
实体类 Data HeadRowHeight(50) ContentStyle(horizontalAlignment HorizontalAlignmentEnum.CENTER, verticalAlignment VerticalAlignmentEnum.CENTER, wrapped BooleanEnum.TRUE) public class CriterionDataExportDTO {ColumnWidth(15)ExcelProperty(value "所属…...
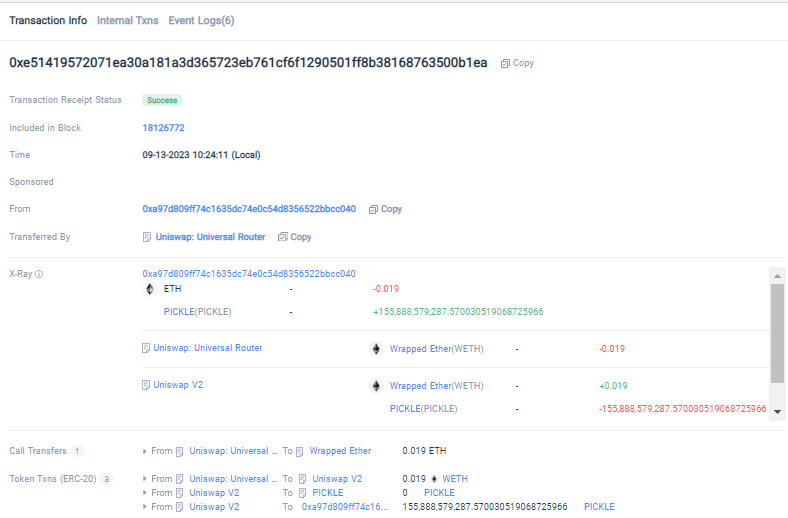
Tokenview X-ray功能:深入探索EVM系列浏览器的全新视角
Tokenview作为一家领先的多链区块浏览器,为了进一步优化区块链用户的使用体验,我们推出了X-ray(余额透视)功能。该功能将帮助您深入了解EVM系列浏览器上每个地址的交易过程,以一种直观、简洁的方式呈现地址的进出账情况…...
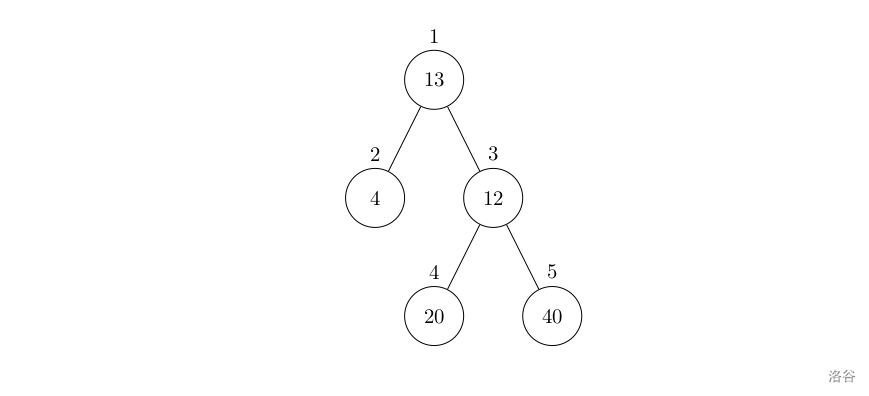
【洛谷 P1364】医院设置 题解(图论+深度优先搜索)
医院设置 题目描述 设有一棵二叉树,如图: 其中,圈中的数字表示结点中居民的人口。圈边上数字表示结点编号,现在要求在某个结点上建立一个医院,使所有居民所走的路程之和为最小,同时约定,相邻接…...

【Java基础】- RMI原理和使用详解
【Java基础】- RMI原理和使用详解 文章目录 【Java基础】- RMI原理和使用详解一、什么RMI二、RMI原理2.1 工作原理图2.2 工作原理 三、RMI远程调用步骤3.1 RMI远程调用运行流程图3.2 RMI 远程调用步骤 四、JAVA RMI简单实现4.1 如何实现一个RMI程序4.2 JAVA实现RMI程序 一、什么…...

无水印免费4K视频素材网站 可商用-Free Stock Video
Free Stock Video是一个在线无水印免费4K视频素材网站,提供各种类型的4k、1080p的视频素材共免费下载,包括美食、水、自然、冬季、无人机、云朵、慢动作、夕阳、动态背景、缩时摄影、旅游和烟火,也可通过关键词搜索方式找到相关视频素材内容&…...

kubesphere中间件部署
微服务部署前中间件部署 一、MySQL部署 1.1 使用Docker实现MySQL主从复制 docker run -p 3307:3306 --name mysql-master \ -v /mydata/mysql/master/log:/var/log/mysql \ -v /mydata/mysql/master/data:/var/lib/mysql \ -v /mydata/mysql/master/conf:/etc/mysql \ -e My…...

使用 AWS S3 SDK 访问 COS-腾讯云国际站代充
腾讯云国际站对象存储(Cloud Object Storage,COS)提供了 AWS S3 兼容的 API,因此当用户的数据从 S3 迁移到 COS 之后,只需要进行简单的配置修改,即可让客户端应用轻松兼容 COS 服务。下面unirech小编主要介…...

c语言每日一练(15)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,上学期间将看学业情况更新。 五道选择题: 1、程序运行的结果…...
如何利用软文推广进行SEO优化(打造优质软文,提升网站排名)
在当今的互联网时代,SEO优化成为了网站推广的关键。而软文推广作为一种有效的推广方式,其优点不仅仅局限于SEO,还可以带来更多的曝光和用户流量。本文将深入探讨如何做好软文推广,从而提升网站排名和流量。 了解目标受众群体 内容…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
