贝塞尔曲线的一些资料收集
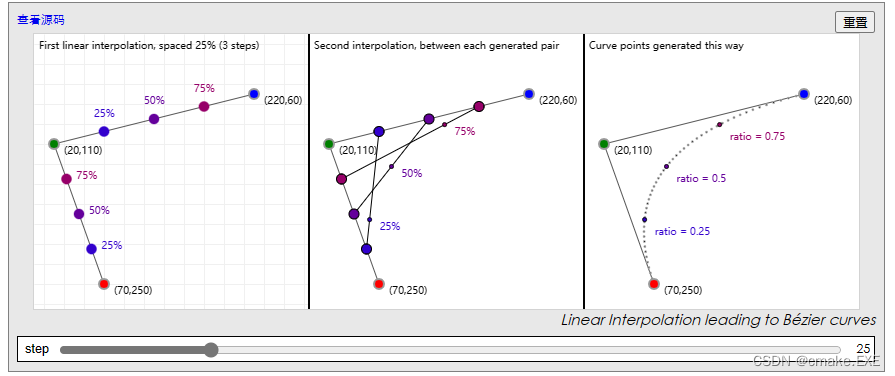
一本免费的在线书籍,供你在非常需要了解如何处理贝塞尔相关的事情。
https://pomax.github.io/bezierinfo/zh-CN/index.html
An algorithm to find bounding box of closed bezier curves? - Stack Overflow
https://stackoverflow.com/questions/2587751/an-algorithm-to-find-bounding-box-of-closed-bezier-curves
前端动画之贝塞尔曲线推导及应用-CSDN博客
https://blog.csdn.net/frontend_frank/article/details/123437040
贝塞尔曲线在线绘制🚀
https://www.bezier-curve.com/
Calculating / Computing the Bounding Box of Cubic Bezier https://floris.briolas.nl/floris/2009/10/bounding-box-of-cubic-bezier/
获取三阶贝塞尔曲线的最小包围盒
c# https://floris.briolas.nl/floris/2009/10/bounding-box-of-cubic-bezier/
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Drawing;namespace BoundingBoxTestProject
{
public static class BezierOp
{public delegate TResult Func<T1, T2, T3, T4, T5, TResult>(T1 arg1, T2 arg2, T3 arg3, T4 arg4, T5 arg5);//cubic polinomal//x = At^3 + Bt^2 + Ct + D//where A,B,C,D://A = p3 -3 * p2 + 3 * p1 - p0//B = 3 * p2 - 6 * p1 +3 * p0//C = 3 * p1 - 3 * p0//D = p0 public static Func<double, double, double, double, double, double> bezierSpline = (p0, p1, p2, p3, t) =>(p3 - 3 * p2 + 3 * p1 - p0) * Math.Pow(t, 3)+ (3 * p2 - 6 * p1 + 3 * p0) * Math.Pow(t, 2)+ (3 * p1 - 3 * p0) * t+ (p0);//X = At^3 + Bt^2 + Ct + D//where A,B,C,D://A = (p3 -3 * p2 + 3 * p1 - p0)//B = (3 * p2 - 6 * p1 +3 * p0)//C = (3 * p1 - 3 * p0)//D = (p0)//We would like to know the values of t where X = 0//X = (p3-3*p2+3*p1-p0)t^3 + (3*p2-6*p1+3*p0)t^2 + (3*p1-3*p0)t + (p0)//Derivetive ://X' = 3(p3-3*p2+3*p1-p0)t^(3-1) + 2(6*p2-12*p1+6*p0)t^(2-1) + 1(3*p1-3*p0)t^(1-1) [f(x)=aX^n => f'(x)=a*n*X^(n-1) remember?]//simplified://X' = (3*p3-9*p2+9*p1-3*p0)t^2 + (6*p2-12*p1+6*p0)t + (3*p1-3*p0)//**!!reusing a,b,and c!!!***//taken as aX^2 + bX + c a,b and c are: public static Func<double, double, double, double, double> A = (p0, p1, p2, p3) => 3 * p3 - 9 * p2 + 9 * p1 - 3 * p0;//ommitting power 2 for now public static Func<double, double, double, double> B = (p0, p1, p2) => 6 * p2 - 12 * p1 + 6 * p0;public static Func<double, double, double> C = (p0, p1) => 3 * p1 - 3 * p0;//b^2 - 4ac = Determinantpublic static Func<double, double, double, double> Determinant = (a, b, c) => Math.Pow(b, 2) - 4d * a * c;public static Func<double, double, double, double[]> Solve = (a, b, c) =>{Func<double, double, double, bool, double> _Solve =(a_, b_, c_, s) =>(-b_ +(Math.Sqrt((b_ * b_) - (4d * a_ * c_)) *((s) ? 1d : -1d))) / (2d * a_);double d = Determinant(a, b, c);if (d < 0)return new double[] { };if (a == 0)//aX^2 + bX + c well then then this is a simple line//x= -c / breturn new double[] { -c / b };if (d == 0){return new double[] { _Solve(a, b, c, true) };}elsereturn new double[]{_Solve(a, b, c, true),_Solve(a, b, c, false)};};public static RectangleF GetRect(PointF p1, PointF c1, PointF c2, PointF p2){double aX = A(p1.X, c1.X, c2.X, p2.X);double bX = B(p1.X, c1.X, c2.X);double cX = C(p1.X, c1.X);double aY = A(p1.Y, c1.Y, c2.Y, p2.Y);double bY = B(p1.Y, c1.Y, c2.Y);double cY = C(p1.Y, c1.Y);var resX = Solve(aX, bX, cX).Where(t => (t >= 0) && (t <= 1)); //solve for t ==0 & filtervar resY = Solve(aY, bY, cY).Where(t => (t >= 0) && (t <= 1)); //solve for t ==0 & filter//Draw min and max;List<PointF> _BBox = new List<PointF>();_BBox.Add(p1); //Add Begin and end point not the control points!_BBox.Add(p2);foreach (var e in resX.Union(resY)){double x = bezierSpline(p1.X, c1.X, c2.X, p2.X, e);double y = bezierSpline(p1.Y, c1.Y, c2.Y, p2.Y, e);PointF p = new PointF((float)x, (float)y);_BBox.Add(p);}float minX = float.MaxValue;float minY = float.MaxValue;float maxX = float.MinValue;float maxY = float.MinValue;foreach (var e in _BBox) //find the bounding box.{minX = Math.Min(e.X, minX);minY = Math.Min(e.Y, minY);maxX = Math.Max(e.X, maxX);maxY = Math.Max(e.Y, maxY);}return new RectangleF(minX, minY, maxX - minX, maxY - minY);}}}
c++ 由上述c#代码改写而来,未做优化
#include <iostream>
#include <vector>
#include <algorithm>
#include <cmath>// 表示一个边界框的结构体
struct BoundingBox {double x; // 左上角 x 坐标double y; // 左上角 y 坐标double width; // 宽度double height; // 高度BoundingBox(double _x, double _y, double _width, double _height) : x(_x), y(_y), width(_width), height(_height) {}
};// 表示一个二维点的结构体
struct Point {double x; // x 坐标double y; // y 坐标Point(double _x, double _y) : x(_x), y(_y) {}
};// 计算三次贝塞尔曲线的值
double bezierSpline(double p0, double p1, double p2, double p3, double t) {double mt = 1 - t;return mt * mt * mt * p0 + 3 * mt * mt * t * p1 + 3 * mt * t * t * p2 + t * t * t * p3;
}// 计算贝塞尔曲线的导数系数
void calculateCoefficients(double p0, double p1, double p2, double p3, double &a, double &b, double &c) {a = 3 * (p3 - 3 * p2 + 3 * p1 - p0);b = 6 * (p2 - 2 * p1 + p0);c = 3 * (p1 - p0);
}// 解二次方程 ax^2 + bx + c = 0,并返回在区间 [0, 1] 内的实数解
std::vector<double> solveQuadratic(double a, double b, double c) {std::vector<double> solutions;// 计算判别式double discriminant = b * b - 4 * a * c;if (discriminant >= 0) {double sqrtDiscriminant = std::sqrt(discriminant);double t1 = (-b + sqrtDiscriminant) / (2 * a);double t2 = (-b - sqrtDiscriminant) / (2 * a);if (t1 >= 0 && t1 <= 1) {solutions.push_back(t1);}if (t2 >= 0 && t2 <= 1) {solutions.push_back(t2);}}return solutions;
}// 计算贝塞尔曲线的边界框
BoundingBox getBoundsOfCurve(double x0, double y0, double x1, double y1, double x2, double y2, double x3, double y3) {double aX, bX, cX, aY, bY, cY;// 计算 x 和 y 方向的导数系数calculateCoefficients(x0, x1, x2, x3, aX, bX, cX);calculateCoefficients(y0, y1, y2, y3, aY, bY, cY);// 找到导数为零的参数值std::vector<double> xSolutions = solveQuadratic(aX, bX, cX);std::vector<double> ySolutions = solveQuadratic(aY, bY, cY);// 存储边界框的点std::vector<Point> bboxPoints;bboxPoints.push_back(Point(x0, y0));bboxPoints.push_back(Point(x3, y3));// 在导数为零的参数值下计算曲线上的点for (double t : xSolutions) {double x = bezierSpline(x0, x1, x2, x3, t);double y = bezierSpline(y0, y1, y2, y3, t);bboxPoints.push_back(Point(x, y));}for (double t : ySolutions) {double x = bezierSpline(x0, x1, x2, x3, t);double y = bezierSpline(y0, y1, y2, y3, t);bboxPoints.push_back(Point(x, y));}// 计算边界框的坐标double minX = bboxPoints[0].x;double minY = bboxPoints[0].y;double maxX = bboxPoints[0].x;double maxY = bboxPoints[0].y;for (const Point &point : bboxPoints) {minX = std::min(minX, point.x);minY = std::min(minY, point.y);maxX = std::max(maxX, point.x);maxY = std::max(maxY, point.y);}// 创建边界框并返回return BoundingBox(minX, minY, maxX - minX, maxY - minY);
}int main()
{// 定义四个控制点的坐标// double x0 = 300.0, y0 = 400.0, x1 = 400.0, y1 = 300.0, x2 = 700.0, y2 = 500.0, x3 = 500.0, y3 = 500.0;double x0 = 300.0, y0 = 400.0, x1 = 400.0, y1 = 600.0, x2 = 700.0, y2 = 500.0, x3 = 500.0, y3 = 500.0;// 计算贝塞尔曲线的边界框BoundingBox bounds = getBoundsOfCurve(x0, y0, x1, y1, x2, y2, x3, y3);std::cout << "Bounding Box: (" << bounds.x << ", " << bounds.y << ") - Width: " << bounds.width << ", Height: " << bounds.height;return 0;
}// Bounding Box: (300, 400) - Width: 267.277, Height: 125
相关文章:

贝塞尔曲线的一些资料收集
一本免费的在线书籍,供你在非常需要了解如何处理贝塞尔相关的事情。 https://pomax.github.io/bezierinfo/zh-CN/index.html An algorithm to find bounding box of closed bezier curves? - Stack Overflow https://stackoverflow.com/questions/2587751/an-algo…...

计算机网络原理 运输层
一,运输层协议概述 1,进程之间的通信 从通信和信息处理的角度看,运输层向它上面的应用层提供通信服务,它属于面向通信部分的最高层,同时也是用户功能中的最底层。当网络边缘部分的两台主机使用网络核心部分的功能进行…...

【JavaEE】多线程案例-阻塞队列
1. 前言 阻塞队列(BlockingQueue)是一个支持两个附加操作的队列。这两个附加的操作是: 在队列为空时,获取元素的线程会等待队列变为非空当队列满时,存储元素的线程会等待队列可用 阻塞队列常用于生产者和消费者的场…...
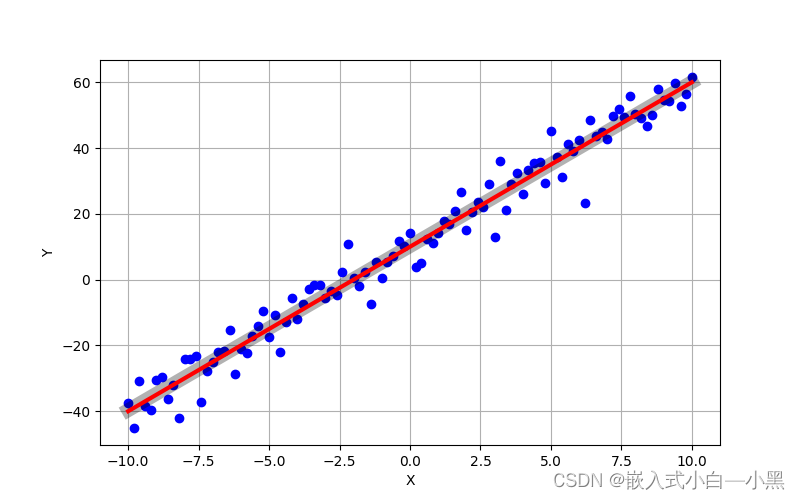
【物联网】简要介绍最小二乘法—C语言实现
最小二乘法是一种常用的数学方法,用于拟合数据和寻找最佳拟合曲线。它的目标是找到一个函数,使其在数据点上的误差平方和最小化。 文章目录 基本原理最小二乘法的求解应用举例使用C语言实现最小二乘法总结 基本原理 假设我们有一组数据点 ( x 1 , y 1 …...

慢查询SQL如何优化
一.什么是慢SQL? 慢SQL指的是Mysql中执行比较慢的SQL,排查慢SQL最常用的方法是通过慢查询日志来查找慢SQL。Mysql的慢查询日志是Mysql提供的一种日志记录,它用来记录Mysql中响应时间超过long_query_time值的sql,long_query_time的默认时间为10s. 二.查看慢SQL是否…...

UART 通信-使用VIO进行板级验证
串口系列知识分享: (1)串口通信实现-串口发送 (2)串口通信发送多字节数据 (3)串口通信实现-串口接收 (4)UART 通信-使用VIO进行板级验证 (5)串口接收-控制LED闪烁 (6)使用串口发送实现ACX720开发板时钟显示 (7)串口发送+RAM+VGA传图 文章目录 前言一、uart串口协…...

linux 查看可支持的shell
查看可支持的shell linux中支持多种shell类型,所以在shell文件的第一行需要指定所使用的shell #!/bin/bash 指定该脚本使用的是/bin/bash,这样的机制使得我们可以轻松地引用任何的解释器 查看该linux系统支持的shell cat /etc/shells/bin/sh/bin/bash/us…...

微服务简介
微服务简介 微服务架构是一种软件架构模式,它将一个大型应用程序拆分为一组小型、独立的服务,每个服务都有自己的业务逻辑和数据存储。这些服务可以独立开发、部署和扩展,通常使用HTTP或其他轻量级通信协议进行通信。 以下是微服务架构的一…...
PHP自己的框架2.0设置常量并绑定容器(重构篇三)
目录 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 3、将常量绑定到容器中 4、运行效果 1、设置常量并绑定容器 2、容器增加设置当前容器的实例和绑定一个类实例当容器 //设置当前容器的实例public static function setInstance($instance){…...

重建大师提交空三后引擎状态是等待,怎么开启?
答:图片中这是在自由网空三阶段,整个AT都是等待中,可以修改任务目录和监控目录看一下,先设置引擎,再提交空三。...
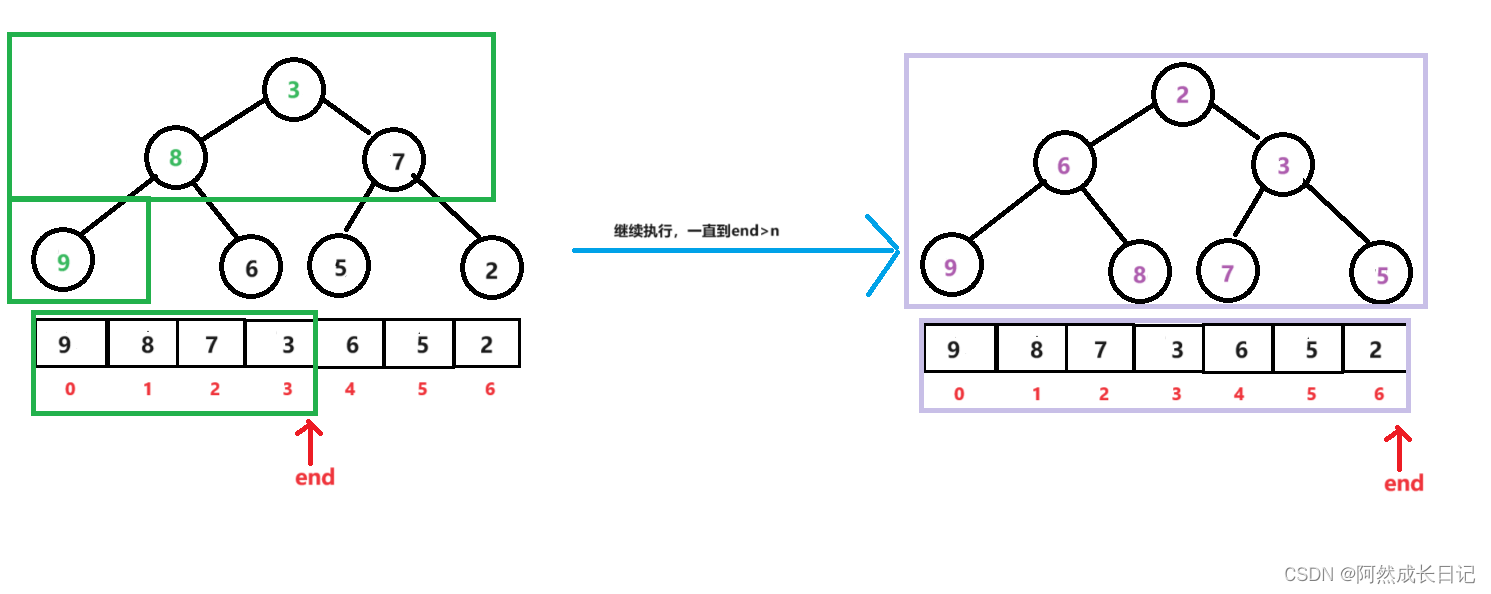
【数据结构】堆的向上调整和向下调整以及相关方法
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃 文章目录 一、堆的概念二、堆的性质…...

【蓝桥杯选拔赛真题60】Scratch旋转风车 少儿编程scratch图形化编程 蓝桥杯选拔赛真题解析
目录 scratch旋转风车 一、题目要求 编程实现 二、案例分析 1、角色分析...

JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析
JavaSE、JavaEE与Spring的概念和异同点剖析以及规范13 个分析 目录概述需求: 设计思路实现思路分析1.什么是JavaSE2.是JavaEE3.什么是Spring 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full busy&…...
微信小程序的图书馆图书借阅 座位预约系统 读者端设计与实现
该系统基于B/S即所谓浏览器/服务器模式,应用springboot框架,选择MySQL作为后台数据库。系统主要包括系统图书信息、图书借阅、图书归还、自习室信息、自习室预约等功能模块。 关键词 微信小程序的图书馆读者端;微信小程序;java语…...
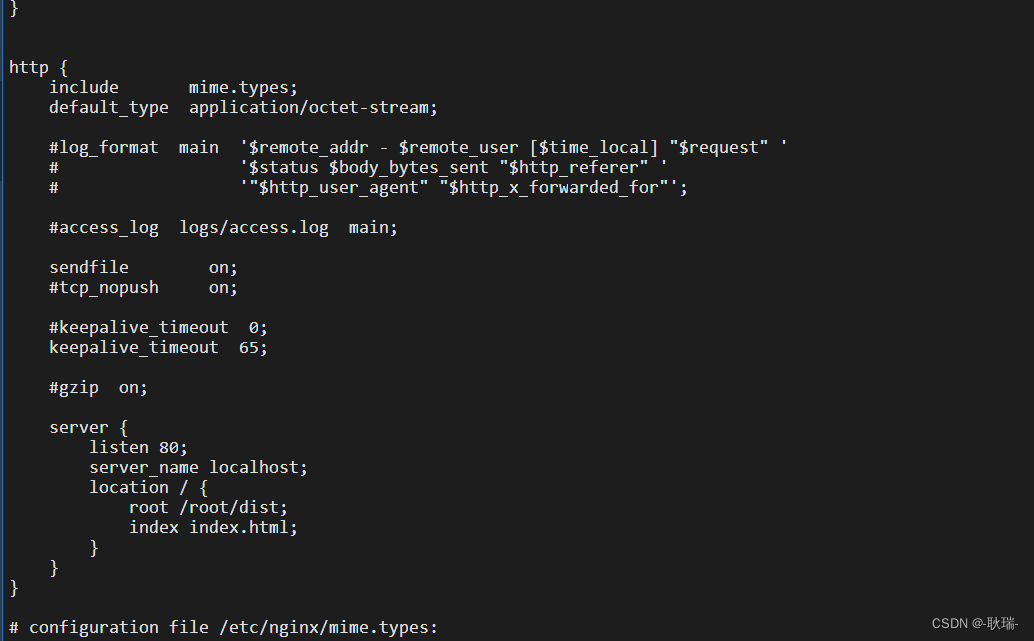
在阿里云 linux 服务器上查看当前服务器的Nginx配置信息
我们可以通过命令 sudo nginx -t查看到nginx.conf的路径 可以通过 sudo nginx -T查看 nginx 详细配置信息,包括加载的配置文件和配置块的内容 其中也会包括配置文件的内容...

专业招投标书翻译怎样做比较好
在全球经济贸易一体化不断深入的时代,招投标作为国际通用的新型贸易方式,受到了大量中外企业的青睐。根据国际惯例,与招标采购活动有关的一切文件资料,均须使用英文编制。即使允许使用非英文语言编制,也必须随附一份英…...
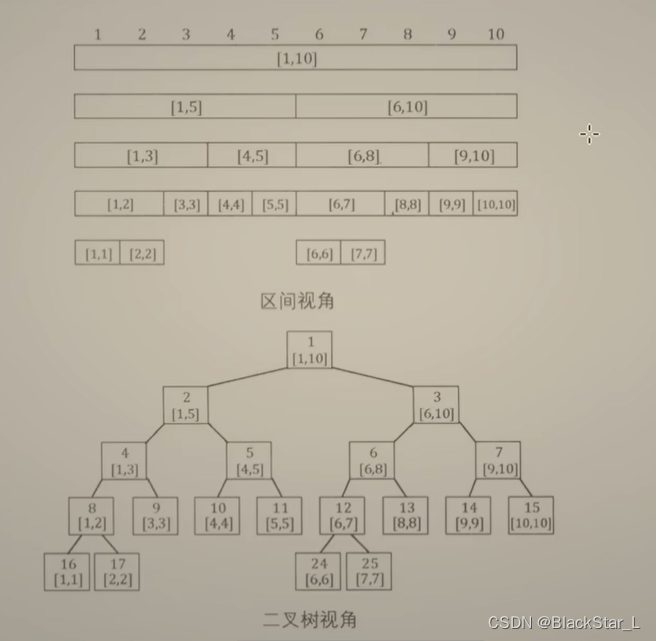
算法总结10 线段树
算法总结10 线段树 线段树2569. 更新数组后处理求和查询 线段树 有一个数组,我们要: 更新数组的值(例如:都加上一个数,把子数组内的元素取反)查询一个子数组的值(例如:求和&#x…...

518抽奖软件,支持按人像照片抽奖
518抽奖软件简介 518抽奖软件,518我要发,超好用的年会抽奖软件,简约设计风格。 包含文字号码抽奖、照片抽奖两种模式,支持姓名抽奖、号码抽奖、数字抽奖、照片抽奖。(www.518cj.net) 照片抽奖模式 圆角边框 照片抽奖模式下&am…...
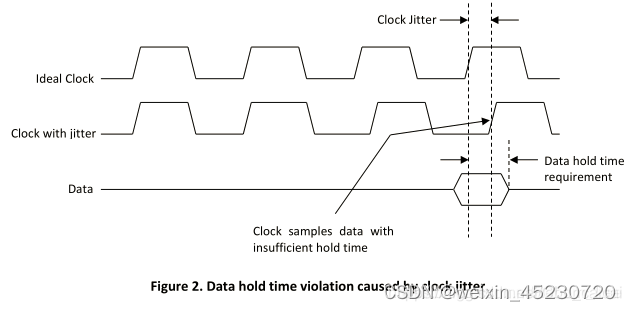
数字IC笔试面试题之--时钟偏斜(skew)与抖动(jitter)
1 时钟偏斜(clock skew) 时钟偏斜(偏移)是因为布线长度和负载不同,导致同一时钟上升沿到不同触发器的时间不同。这一时间差,即为时钟偏移。 时钟偏斜可能导致时序违例(本文直接粘贴了参考博客…...

免费api接口:物流api,企业工商查询api,游戏api。。。
免费api接口,物流api,企业工商查询api,游戏api。。。都有。 Facebook Games Services - Facebook Games Services 为游戏开发者提供了各种服务, 包括(但不限于) 成就 API, 分数 API, 应用通知, 请求, 游戏养成和 Facebook SDK for Unity.Google Play Games Service…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...
