扩散模型在图像生成中的应用:从真实样例到逼真图像的奇妙转变
一、扩散模型
扩散模型的起源可以追溯到热力学中的扩散过程。热力学中的扩散过程是指物质从高浓度往低浓度的地方流动,最终达到一种动态的平衡。这个过程就是一个扩散过程。
在深度学习领域中,扩散模型(diffusion models)是深度生成模型中新的SOTA。 扩散模型在图片生成任务中超越了原SOTA:GAN,并且在诸多应用领域都有出色的表现,如计算机视觉、NLP、波形信号处理、多模态建模、分子图建模、时间序列建模、对抗性净化等。
1、扩散模型原理介绍
在深度学习中,生成模型的目标是根据给定的样本(训练数据)生成新样本。首先给定一批训练数据
,假设其服从某种复杂的真实分布
,则给定的训练数据可视为从该分布中采样的观测样本
。如果能从这批观测样本中估计出训练数据的真实分布,就可以从该分布中源源不断地采样出新的样本。
生成模型作用是估计训练数据的真实分布,并将其假定为
,这个过程称为拟合网络。
如何确定估计的分布和真实分布
的差距?
要求所有的训练数据样本采样自
的概率最大,主要思想就是统计学中的最大似然估计思想,这也是生成模型的基本思想之一,因此生成模型的学习目标就是对训练数据的分布进行建模。
公认最早的扩散模型DDPM(Denoing Diffusion Probalilistic Model)的扩散模型原理就由此而来,扩散过程如下图所示,具体分为前向过程和反向过程两部分:
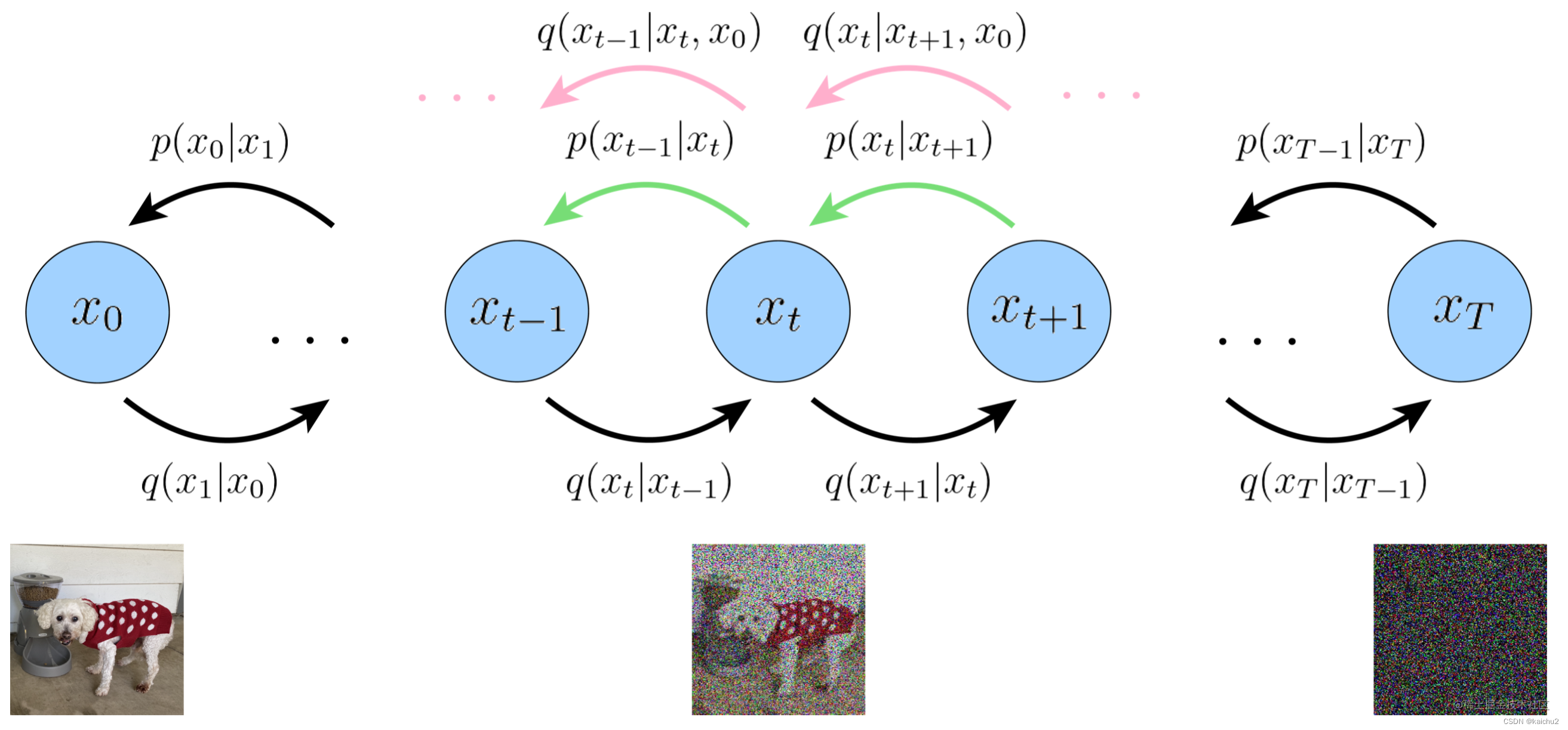
1.1、扩散模型前向过程
前向过程是给数据中添加噪声的过程,假设给定一批训练数据,数据分布为 ,其中,0表示初始状态,即还没有开始扩散,即上图的原图(小狗)。
如上所述,将前向加噪声过程分为离散的多个时间步,在每一个时间步
,给上一个时间步
的数据
添加高斯噪声,从而生成带有噪声(简称“带噪”)的数据
,同时数据
也会被送入下一个时间步
以继续添加噪声。其中,噪声的方差由一个位于区间(0,1)的固定值
和当前时刻“带噪”的数据分布确定。在反复迭代和加噪(即添加噪声)
次之后,只要
足够大,根据马尔可夫链的性质就可以得到纯随机噪声分布的数据,即类似稳定墨水系统的状态。
马尔可夫链:是马尔可夫过程的原始模型,也是一个表示状态转移的离散随机过程。该离散过程具有“无记忆”的性质,即下一状态的概率分布仅由当前状态表示,而与之前的所有状态无关,同时只要时间序列足够长,即状态转移的次数足够多,最终的概率分布将趋于稳定。
1.1.1、扩散模型公式
从时间步 到时间步
的单步扩散加噪声过程的数学表达式如下:
(1)

最终的噪声分布数学表达式如下:
(2)
1.2、扩散模型反向过程
前向过程是将数据噪声化的过程(增加噪声),反向过程则是“去噪”的过程,即从随机噪声中迭代恢复出清晰数据的过程。从采样自高斯噪声 的一个随机噪声中恢复出原始数据
,就需要知道反向过程中每一步的图像分布状态转移。DDPM也将这个方向过程定义为马尔可夫链,由一系列用神经网络参数化的高斯分布组成的,也就是需要训练的扩散模型。
从时间步 到时间步
的单步反向去噪的过程,公式如下所示:
由于反向过程的每一步都是参数化的高斯分布,因此可以分布求高斯分布的均值和方差。经过贝叶斯公式推导
上式巧妙地通过贝叶斯公式将逆向过程转换为前向过程,且最终得到的概率密度函数和高斯概率密度函数的指数部分,
相对应。其中,是与
无关的常数项。令
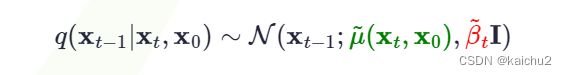
这个公式表示的是高斯分布(正态分布)的概率密度函数,其中:
-
是当前时刻的观测值;
-和
分别是前一次和前几次的观测值;
-是预测值,即使用贝叶斯方法预测出来的下一个时刻的值;
-是预测误差的方差,也就是预测值与实际值之间的差异程度。
这个公式的意义在于,根据已知的前几次观测值和当前时刻的观测值,使用贝叶斯方法预测出下一个时刻的观测值,并计算出预测误差的方差。这个预测值和预测误差的方差可以用来评估模型的准确性和稳定性。
将绿色部分与红色部分一一对应,一是计算平滑后的数据 ,二是计算平滑后的条件期望
。
1. 平滑后的数据 :
这里,和
分别表示第
个观测值和前一个观测值的条件期望。
是平滑因子,用于调整数据的平滑程度。
2. 平滑后的条件期望 :
这里,使用了一个加权平均的方法来计算条件期望。具体来说,我们将当前观测值的预测值乘以平滑因子,然后加上前一个观测值的预测值乘以平滑因子。最后,将结果除以平滑因子的倒数。
这两个公式可以帮助我们在贝叶斯推倒扩散模型中对数据进行平滑处理,从而得到更加稳定和可靠的预测结果。
从上述可以看出,方差是一个定量(扩散过程参数固定),而均值是一个依赖于和
的函数,因此需要使用扩散模型来优化参数。(此部分推导过程参考 扩散模型Diffusion Model原理)
贝叶斯分类器基本原理:
当事件B发生时,事件A发生的条件概率可以表示为:
其中,$P(AB)$表示事件A和事件B同时发生的概率;$P(B)$表示事件B发生的概率。根据全概率公式,有:
其中,
表示在事件A发生的情况下,事件B发生的概率;
表示在事件A不发生的情况下,事件B发生的概率;
表示事件A不发生的概率。将上述两个式子代入上式,得到:
因此,当事件B发生时,事件A发生的概率为1,即
。
二、极大似然估计原理
极大似然估计的原理目的是利用已知的样本结果,反推最有可能(最大概率)导致这种结果的参数值。 极大似然估计是建立在极大似然原理的基础上的一个统计方法,极大似然估计提供了一种给定观测数据来评估模型参数的方法,即“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率最大,则称为极大似然估计。
由于样本集中的样本都是独立同分布的,可以只考虑一类样本集,来估计参数向量
,假设已知的样本集为:
联合概率密度函数 称为相对于
的
似然函数。
如果 是参数空间中能够使似然函数
最大的值,则
应该是 "最可能" 的参数值,那么
就是
的极大似然估计量。它是样本集的函数,记作:
称为极大似然估计函数估计值。
三、极大似然估计例子
假设有两个外形完全相同的箱子,1号箱子中有99只白球,1只黑球;2号箱子中只有1只白球,99只黑球。在一次实验中取出黑球,请问是从哪个箱子中取出的?
人们通常会猜测这只黑球最像是从2号箱取出来的,此时描述的“最像”就有“极大似然”的意思,这种想法常称为“极大似然原理”。
最大似然估计是一种参数估计的方法,它是概率论在统计学的应用之一。
最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大,我们当然不会再去选择其他小概率的样本,所以干脆就把这个参数作为估计的真实值。
举个例子,假设我们有一组数据,其中包含了一些人的年龄和收入信息。我们想要估计这些人的平均年龄和平均收入。根据最大似然估计的思想,我们应该尽量让这组数据符合真实情况。也就是说,如果我们假设这些人的平均年龄是30岁,那么当这组数据中有人年龄确实为30岁时,我们就认为这个假设是正确的;如果有人年龄不是30岁,但其他方面都符合条件,我们也认为这个假设是正确的。同样地,如果我们假设这些人的平均收入是5000元/月,那么当这组数据中有人收入确实为5000元/月时,我们就认为这个假设是正确的;如果有人收入不是5000元/月,但其他方面都符合条件,我们也认为这个假设是正确的。
因此,在最大似然估计中,我们需要根据实际情况来选择合适的参数值。
四、优化目标
扩散模型预测的噪声残差,即要求后向过程中预测的噪声分布与前向过程中施加的噪声分布之间的“距离”最小。扩散模型的最终优化目标的数学表达式如下:
其中,可以看出,在训练DDPM时,只要用一个简单的MSE(均方误差)损失最小化前向过程施加的噪声分布和后向过程预测的噪声分布,就能实现最终的优化目标。
五、从零开始搭建扩散模型(代码实现)
5.1、导入相关的包
导入所需的相关库:采用diffusers提供的DDPM模型接口
注:可能会遇到一些安装包问题,可采用下面的pip源
| 安装源 | 指令 |
|---|---|
| pip默认的 | pip install XXX |
| 清华大学源 | |
| 豆瓣源 | |
| 阿里云源 | |
import torch
import torchvision
from torch import nn
from torch.nn import functional as F
from torch.utils.data import DataLoader
from diffusers import DDPMScheduler,UNet2DModel
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings("ignore")device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)注:本文的代码都是在colab中实现,本地也可以运行。
5.2、数据集测试
本文采用官方提供的一个小型测试集FashMNIST:torchvision.datasets.FashionMNIST(包含10个类别),当然也可以使用其他测试集,这里主要是过一遍流程
dataset = torchvision.datasets.FashionMNIST(root="./FashionMNIST",train=True,download=True,transform=torchvision.transforms.ToTensor())
train_dataloader = DataLoader(dataset,batch_size=8,shuffle=True)
image,label = next(iter(train_dataloader))
print("image shape:",image.shape)
print("Label:",label)# 查看数据的类别:10个类
classes_list = dataset.classes
print(classes_list)
plt.imshow(torchvision.utils.make_grid(image)[0],cmap="Greys")输出:
image shape: torch.Size([8, 1, 28, 28])
Label: tensor([4, 3, 5, 8, 8, 1, 4, 3])
['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
5.3、扩散模型之退化过程
在扩散过程中需要为内容加入噪声,如何通过一个简单的方法控制图像的损坏程度,可以引入一个参数控制输入的“噪声量”。如下图绿色箭头方向(给图像中加入噪声)。

主要方法:将噪声张量与输入图像相乘,并将结果与1减去噪声的比例相加,以实现损坏效果
代码实现:
# 通过引入一个参数来控制输入的“噪声”来控制内容的损坏的程度
noise = torch.rand_like(image)def corrupt(image,amount):"""根据p为输入image添加噪声,这就是退化过程"""noise = torch.rand_like(image)amount = amount.view(-1,1,1,1)print(amount.shape)return image*(1-amount)+noise*amount# 对输出结果进行可视化
fig,axs = plt.subplots(2,1,figsize=(10,5))
axs[0].set_title("Input data")
axs[0].imshow(torchvision.utils.make_grid(image)[0],cmap="Greys")# 加入噪声:获得一个一维张量,包含从0-1之间的均匀分布的数值
p = torch.linspace(0,1,image.shape[0])
print(p.shape)
noised_image = corrupt(image,p)
print(noised_image.shape)
# 绘制加噪声的图像
axs[1].set_title("corrupt data")
axs[1].imshow(torchvision.utils.make_grid(noised_image)[0],cmap="Greys")输出:
torch.Size([8])
torch.Size([8, 1, 1, 1])
torch.Size([8, 1, 28, 28])
5.3.1、其他噪声
图像中常见的噪声有以下四种:高斯噪声,泊松噪声,乘性噪声,椒盐噪声。
高斯噪声:是指其概率密度函数服从高斯分布(即正态分布)的一类噪声。如果一个噪声,它的幅度分布服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。高斯白噪声的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。产生原因:1)图像传感器在拍摄时视场不够明亮、亮度不够均匀;2)电路各元器件自身噪声和相互影响;3)图像传感器长期工作,温度过高。
泊松噪声:是指像素点出现的概率不是固定的,而是在某个范围内随机波动的一种噪声。产生原因:1)图像传感器在拍摄时视场不够明亮、亮度不够均匀;2)电路各元器件自身噪声和相互影响;3)图像传感器长期工作,温度过高。
乘性噪声:是指将两个或多个低频信号相乘后得到高频信号再进行处理时产生的伪像。产生原因:1)图像传感器在拍摄时视场不够明亮、亮度不够均匀;2)电路各元器件自身噪声和相互影响;3)图像传感器长期工作,温度过高。
椒盐噪声:是指由于图像切割引起的黑白相间的亮暗点噪声,与图像信号的关系是相乘。产生原因:1)图像传感器在拍摄时视场不够明亮、亮度不够均匀;2)电路各元器件自身噪声和相互影响;3)图像传感器长期工作,温度过高。
(1)高斯噪声
高斯噪声是一种通过向输入数据添加均值为零和标准差 (σ)的正态分布随机值而产生的噪声。 正态分布,也称为高斯分布,是一种连续概率分布,由其概率密度函数 (PDF) 定义:
其中是随机变量,
是均值,
是标准差。高斯噪声在数字信号处理中被广泛应用,例如在通信、图像处理、语音识别等领域。
# 读取一张图像并将图像和高斯噪声合并
import numpy as np
import matplotlib.pyplot as plt
import cv2# 读取图像
image = cv2.imread('./image/2008_000536.jpg', cv2.IMREAD_GRAYSCALE)# 设置参数
mu = 0
sigma = 1
size = image.shape# 生成高斯噪声
noise = np.random.normal(mu, sigma, size)# 将高斯噪声添加到图像上
noisy_image = image + noise# 显示原始图像和带噪声的图像
plt.subplot(131), plt.imshow(image,cmap="gray"), plt.title('Original Image')
plt.subplot(132), plt.imshow(noise), plt.title('Noise')
plt.subplot(133), plt.imshow(noisy_image,cmap="gray"), plt.title('Noisy Image')
plt.show()
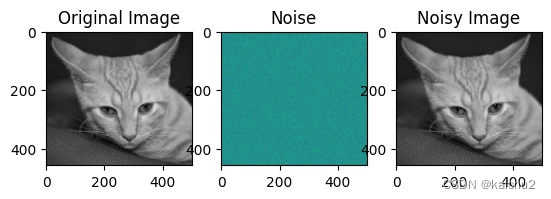
(2)椒盐噪声
椒盐噪声是一种图像噪声,通常是由于图像切割引起的黑白相间的亮暗点噪声,与图像信号的关系是相乘。椒盐噪声的成因可能是影像讯号受到突如其来的强烈干扰而产生、类比数位转换器或位元传输错误等。例如失效的感应器导致像素值为最小值,饱和的感应器导致像素值为最大值 。
在数字图像中,椒盐噪声是一种因为信号脉冲强度引起的噪声,可以用中值滤波来消除。给一副数字图像加上椒盐噪声的步骤如下:指定信噪比 SNR (其取值范围在 [0, 1]之间)计算总像素数目 SP,得到要加噪的像素数目 NP = SP * (1-SNR)随机获得要加噪的像素位置。
计算步骤如下:
1. 指定信噪比SNR(其取值范围在[0, 1]之间)。
2. 计算总像素数目SP。
3. 根据信噪比和总像素数目计算要加噪的像素数目NP = SP * (1-SNR)。
4. 随机获得要加噪的像素位置,即在图像中随机选择NP个像素点。
5. 对于每个被选中的像素点,将其值设置为一个随机数,这个随机数的范围在图像的最大值和最小值之间。
6. 将加噪后的图像保存或显示出来。
代码实现:
# 添加椒盐噪声
import random
# 在原图中增加椒盐噪声
def salt_and_pepper_noise(image, prob):output = np.zeros(image.shape, np.uint8)thres = 1 - prob for i in range(image.shape[0]):for j in range(image.shape[1]):rdn = random.random()if rdn < prob:output[i][j] = 0elif rdn > thres:output[i][j] = 255else:output[i][j] = image[i][j]return output# 生产指定大小的椒盐噪声
def generate_salt_pepper_noise(size, salt_ratio=0.05, pepper_ratio=0.05):# 创建一个大小为size的空数组noise = np.zeros((size, size))# 遍历数组中的每个元素for i in range(size):for j in range(size):# 计算当前元素的盐和胡椒概率salt_prob = salt_ratiopepper_prob = pepper_ratio# 如果当前元素位于边缘,则增加胡椒概率if i == 0 or i == size - 1 or j == 0 or j == size - 1:pepper_prob += 0.05# 随机选择盐或胡椒if np.random.rand() < salt_prob:noise[i, j] = 1elif np.random.rand() < pepper_prob:noise[i, j] = 2return noise# 读取图像
image = cv2.imread('./image/2008_000536.jpg',cv2.COLOR_BGR2GRAY)
pepper_image = generate_salt_pepper_noise(28,0.1)
salt_pepper = salt_and_pepper_noise(image,0.2)
plt.subplot(131),plt.imshow(image),plt.title("Original Image")
plt.subplot(132),plt.imshow(salt_pepper),plt.title("Salt Image")
plt.subplot(133),plt.imshow(pepper_image),plt.title("Pepper Image")
5.4、扩散模型之网络模型
训练模型之前,需要一个能够输入28×28像素的噪声图像,然后输出相同大小图片的预测结果。本文采用经典的Unet网络,由一条“压缩路径”和一条“扩展路径”组成。“压缩路径”主要是通过压缩数据的维度,而“扩展路径”则将数据扩展回原始维度(类似于自动编码器)。
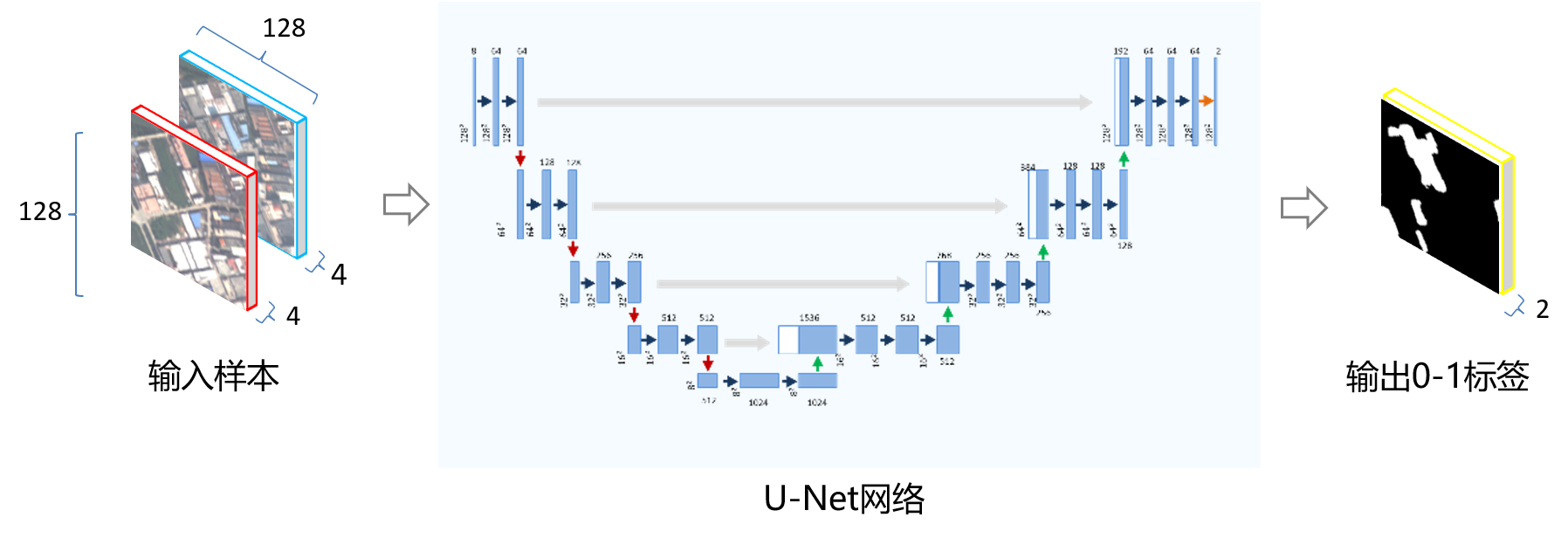
1、自动编码器:
是一种无监督学习模型,主要用于数据压缩和特征提取。它由两部分组成:编码器和解码器。
编码器将输入数据压缩成一个低维表示,解码器则将这个低维表示还原成原始数据。在这个过程中,自动编码器学习如何有效地将原始数据转换为压缩表示,以及如何从压缩表示中恢复原始数据。这种学习过程使得自动编码器能够捕捉到数据中的有用信息,同时去除冗余和噪声。
自动编码器的基本思想是通过训练一个神经网络来最小化输入数据和解码器输出之间的差异(即重构误差)。在训练过程中,网络的权重会不断地更新,以便更好地捕捉数据的特征和结构。
自动编码器在许多领域都有广泛的应用,如图像识别、语音识别、自然语言处理、推荐系统等。它们可以用于降维、特征提取、异常检测、生成模型等任务。
这段代码定义了一个名为BasicNet的类,用于实现Unet网络。Unet网络是一种用于图像分割的卷积神经网络,它包括一个编码器(下采样)和一个解码器(上采样)。这个简单的Unet网络包含三个卷积层和相应的激活函数、池化层和上采样层。
1. `__init__`方法:定义了网络的结构。
- `self.down_layers`:定义了下采样层,包括三个卷积层,每个卷积层后面跟着一个ReLU激活函数和一个最大池化层。
- `self.up_layers`:定义了上采样层,包括三个卷积层,每个卷积层后面跟着一个ReLU激活函数。
- `self.act`:定义了激活函数,这里使用ReLU激活函数。
- `self.downscale`:定义了最大池化层,用于降低特征图的空间尺寸。
- `self.upscale`:定义了上采样层,用于增加特征图的空间尺寸。
2. `forward`方法:实现了网络的前向传播过程。
- 对于下采样层,首先将输入x通过第一个卷积层、激活函数和池化层,然后将结果添加到h列表中,并将x通过最大池化层降维。重复这个过程,直到处理完所有的下采样层。
- 对于上采样层,首先将输入x通过上采样层和激活函数,然后将结果与h列表中的最后一个元素相加,再通过第二个卷积层、激活函数和池化层。重复这个过程,直到处理完所有的上采样层。
- 最后返回x作为网络的输出。
# Unet网络
class BasicNet(nn.Module):"""一个十分简单的Unet网络部署"""def __init__(self,in_channels=1,out_channels=1):super().__init__()self.down_layers = torch.nn.ModuleList([nn.Conv2d(in_channels,32,kernel_size=5,padding=2),nn.Conv2d(32,64,kernel_size=5,padding=2),nn.Conv2d(64,64,kernel_size=5,padding=2),])self.up_layers = torch.nn.ModuleList([nn.Conv2d(64,64,kernel_size=5,padding=2),nn.Conv2d(64,32,kernel_size=5,padding=2),nn.Conv2d(32,out_channels,kernel_size=5,padding=2),])self.act = nn.ReLU()self.downscale = nn.MaxPool2d(2)self.upscale = nn.Upsample(scale_factor=2)def forward(self,x):h = []for i,l in enumerate(self.down_layers):x = self.act(l(x))if i < 2:h.append(x)x = self.downscale(x)for i,l in enumerate(self.up_layers):if i > 0:x = self.upscale(x)x += h.pop()x = self.act(l(x))return xnet = BasicNet()
x = torch.rand(8,1,28,28)
print(net(x).shape)
# 模型参数
sum([param.numel() for param in net.parameters()])
print(net)输出:
torch.Size([8, 1, 28, 28])
BasicNet((down_layers): ModuleList((0): Conv2d(1, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))(1): Conv2d(32, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))(2): Conv2d(64, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)))(up_layers): ModuleList((0): Conv2d(64, 64, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))(1): Conv2d(64, 32, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))(2): Conv2d(32, 1, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2)))(act): ReLU()(downscale): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)(upscale): Upsample(scale_factor=2.0, mode='nearest')
)5.4.1、卷积神经网络
卷积神经网络(Convolutional Neural Networks, CNN)是一类包含卷积计算且具有深度结构的前馈神经网络(Feedforward Neural Networks),是深度学习(deep learning)的代表算法之一。卷积神经网络具有表征学习(representation learning)能力,能够按其阶层结构对输入信息进行平移不变分类(shift-invariant classification),因此也被称为“平移不变人工神经网络(Shift-Invariant Artificial Neural Networks, SIANN)”。
卷积神经网络(Convolutional Neural Networks,简称CNN)是一种具有局部连接、权值共享等特点的深层前馈神经网络。它主要由输入层、卷积层,ReLU层、池化层和全连接层构成。
局部连接是指卷积层的节点仅仅和其前一层的部分节点相连接,只用来学习局部特征。权值共享是指卷积核中的权重在多个位置上共享,这样可以减少参数数量,使运算变得简洁、高效,能够在超大规模数据集上运算 。
卷积层:是CNN的核心部分,它通过卷积核对输入数据进行卷积操作,提取出数据的特征信息。
ReLU层:是卷积层的激活函数,它可以增加网络的非线性性,提高网络的表达能力。
池化层:是对卷积后的数据进行降采样处理,减少数据量,同时保留重要的特征信息。
全连接层:是将卷积层和池化层输出的特征向量转换为最终的输出结果。

简单看下各个网络基本结构的可视化效果:
(1)卷积可视化
import numpy as np
fig,axes = plt.subplots(1,2)
img = image[6][0].to("cpu")
axes[0].set_title("origin image")
axes[0].imshow(img,cmap="Greys")# 卷积
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=2)
# 应用卷积层
output = conv(img.unsqueeze(0))
out = torch.tensor(output)
axes[1].set_title("conv image")
axes[1].imshow(out[0],cmap="Greys")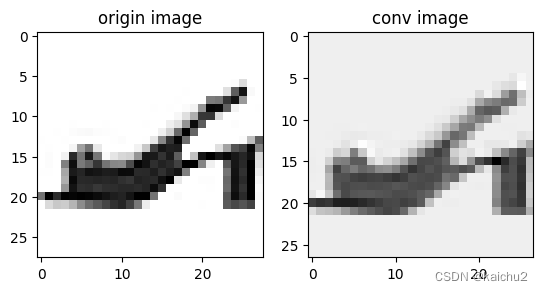
(2)不同卷积核大小的可视化
# 不同卷积核大小下的效果
import numpy as np
fig,axes = plt.subplots(1,6,figsize=(20,5))
img = image[3][0].to("cpu")
axes[0].set_title("origin image")
axes[0].imshow(img,cmap="Greys")# 不同卷积核大小可视化效果
for i in range(1,6):conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=i)# 应用卷积层output = conv(img.unsqueeze(0))out = torch.tensor(output)axes[i].set_title(f"kernel_size:{i}")axes[i].imshow(out[0],cmap="Greys")
(3)池化层可视化
# 池化层操作
import numpy as np
fig,axes = plt.subplots(1,4,figsize=(12,5))
img = image[6][0].to("cpu")
axes[0].set_title("origin image") # cmap="Greys"灰度显示
axes[0].imshow(img)# 卷积
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=2)
# 采用平均池化,尺寸缩小一半
pool = nn.MaxPool2d(kernel_size=2)
avg_pool = nn.AvgPool2d(kernel_size=2)
# 应用卷积层
output = conv(img.unsqueeze(0))
out = torch.tensor(output)
# 最大池化操作,尺寸缩小一半
pool_out = pool(out)
# 平均池化操作,尺寸缩小一半
avg_pool_out = avg_pool(out)
axes[1].set_title("conv image")
axes[1].imshow(out[0])
axes[2].set_title("maxpool image")
axes[2].imshow(pool_out[0])
axes[3].set_title("avgpool image")
axes[3].imshow(avg_pool_out[0])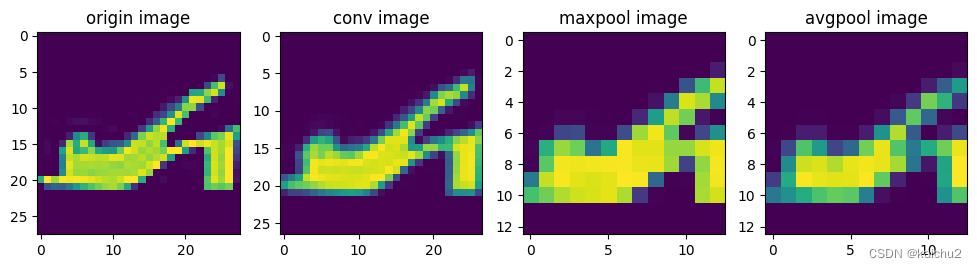
(4)激活函数可视化
import numpy as np
fig,axes = plt.subplots(1,2)
img = image[6][0].to("cpu")
axes[0].set_title("origin image")
axes[0].imshow(img)# 采用激活函数处理之后
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=5,padding=2)
act = nn.ReLU(0.01)
# 应用卷积层
output = conv(img.unsqueeze(0))
out = torch.tensor(output)
act_out = act(out)
axes[1].set_title("LeakyRelu image")
axes[1].imshow(act_out[0])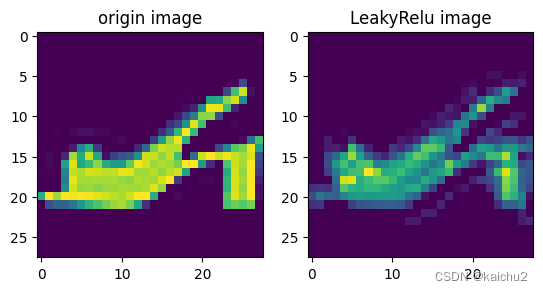
(5)上采样可视化
# 上采样操作
import numpy as np
fig,axes = plt.subplots(1,2)
img = image[6][0].to("cpu")
axes[0].set_title("origin image")
axes[0].imshow(img)
# 采用上采样处理:可以看下图,高度和宽度都增大2倍
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3,padding=2)
act = nn.ReLU(0.01)
upsample = nn.Upsample(scale_factor=(2,2))
output = conv(img.unsqueeze(0))
out = torch.tensor(output)
# Input and scale_factor must have the same number of spatial dimensions, but got input with spatial dimensions of [30] and scale_factor of shape
# 这种情况是需要增加一个维度
upsample_out = upsample(out.unsqueeze(0))
print(upsample_out.shape)
axes[1].set_title("Upsample image")
axes[1].imshow(upsample_out[0][0])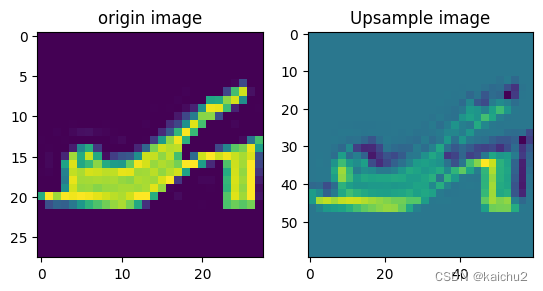
5.5、训练模型
首先给定一个“带噪”(即加入了噪声)的输入noise,扩散模型输出其对原始输入x的最佳预测,我们需要通过均方误差对预测值与真实值进行比较。
均方误差损失(MSE)是回归问题下的损失函数,用于预测对具体数值的预测。它的计算公式为:,其中
是真实值,
是预测值。均方误差损失越小,说明模型预测越准确。
这是一个PyTorch代码片段,它定义了一个优化器对象。
`optimizer = torch.optim.Adam(net.parameters(),lr=1e-3)` 这行代码做了以下事情:
1. `torch.optim.Adam` 是一个实现了Adam优化算法的类。Adam是一种用于深度学习模型的优化算法,它结合了RMSProp和Momentum的优点,可以自适应地调整学习率。
2. `net.parameters()` 是一个生成器,它包含了神经网络中所有的可训练参数。
3. `lr=1e-3` 是设置的学习率,这个值决定了我们在更新模型参数时步长的大小。学习率越小,模型收敛的速度越慢,但可能得到更精确的结果;学习率越大,模型收敛的速度越快,但可能会错过最优解。
所以,这行代码的作用就是创建了一个Adam优化器,用于优化神经网络的参数。
# 数据加载
train_dataloader = DataLoader(dataset,batch_size=128,shuffle=True)
# 训练批次
epochs = 15
# 创建网络
net = BasicNet()
net.to(device)# 定义损失函数
loss_function = nn.MSELoss()# 指定优化器
optimizer = torch.optim.Adam(net.parameters(),lr=1e-3)# 记录训练过程中的损失,供后续查看
losses = []
batch_labels = []
batch_preds = []# train
for epoch in range(epochs):for image,label in train_dataloader:image = image.to(device)# 创建噪声noise = torch.rand(image.shape[0]).to(device)# 创建加入噪声的输入noise_image = corrupt(image,noise)pred = net(noise_image)# 计算损失loss = loss_function(pred,image)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()# 存储损失,供后期查看losses.append(loss.item())# 输出在每个周期训练得到的损失的均值avg_loss = sum(losses[-len(train_dataloader):])/len(train_dataloader)print(f"Finished epoch {epoch}. Average loss for this epoch:{avg_loss:05f}")model_dir = "./model"
import os
if not os.path.exists(model_dir):os.makedirs(model_dir)
# torch.save("./model/model.pth",net)# 查看损失曲线
plt.plot(losses)
plt.ylim(0,0.1)输出:
Finished epoch 0. Average loss for this epoch:0.059535
Finished epoch 1. Average loss for this epoch:0.024476
Finished epoch 2. Average loss for this epoch:0.022848
Finished epoch 3. Average loss for this epoch:0.021662
Finished epoch 4. Average loss for this epoch:0.021025
Finished epoch 5. Average loss for this epoch:0.020682
Finished epoch 6. Average loss for this epoch:0.020176
Finished epoch 7. Average loss for this epoch:0.020124
Finished epoch 8. Average loss for this epoch:0.019379
Finished epoch 9. Average loss for this epoch:0.019473
Finished epoch 10. Average loss for this epoch:0.018823
Finished epoch 11. Average loss for this epoch:0.018897
Finished epoch 12. Average loss for this epoch:0.018471
Finished epoch 13. Average loss for this epoch:0.018010
Finished epoch 14. Average loss for this epoch:0.017308 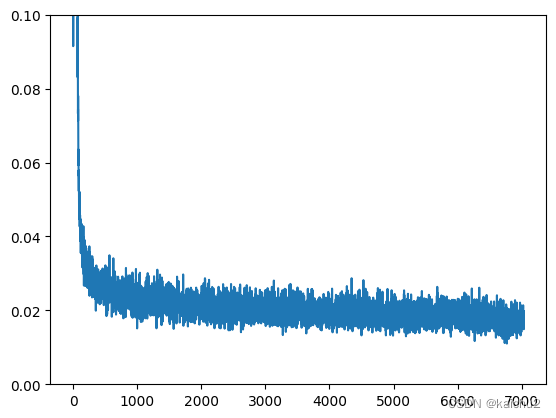
5.6、模型推理
对于噪声量较低的输入,模型的预测结果效果不错,但对于噪声量很好的输入,模型能够获得的信息逐渐减少,当mount=1时,模型将输出一个模糊的预测,预测接近数据集的平均值。
### 测试
test_data = torchvision.datasets.FashionMNIST(root="./FashionMNIST",train=False,transform=torchvision.transforms.ToTensor(),download=True)
test_dataloader = DataLoader(test_data,batch_size=128,shuffle=True)x_test,x_label = next(iter(test_dataloader))
x_test = x_test[:8]# 在0-1之间选择退化量
amount = torch.linspace(0,1,x_test.shape[0])
noised_x_test = corrupt(x_test,amount)# 得到模型的预测结果
with torch.no_grad():preds = net(noised_x_test.to(device)).detach().cpu()# 绘图
fig,axs = plt.subplots(3,1,figsize=(12,7))
axs[0].set_title("Input image")
axs[0].imshow(torchvision.utils.make_grid(x_test)[0].clip(0,1),cmap="Greys")axs[1].set_title("noise image")
axs[1].imshow(torchvision.utils.make_grid(noised_x_test)[0].clip(0,1),cmap="Greys")axs[2].set_title("pred image")
axs[2].imshow(torchvision.utils.make_grid(preds)[0].clip(0,1),cmap="Greys")
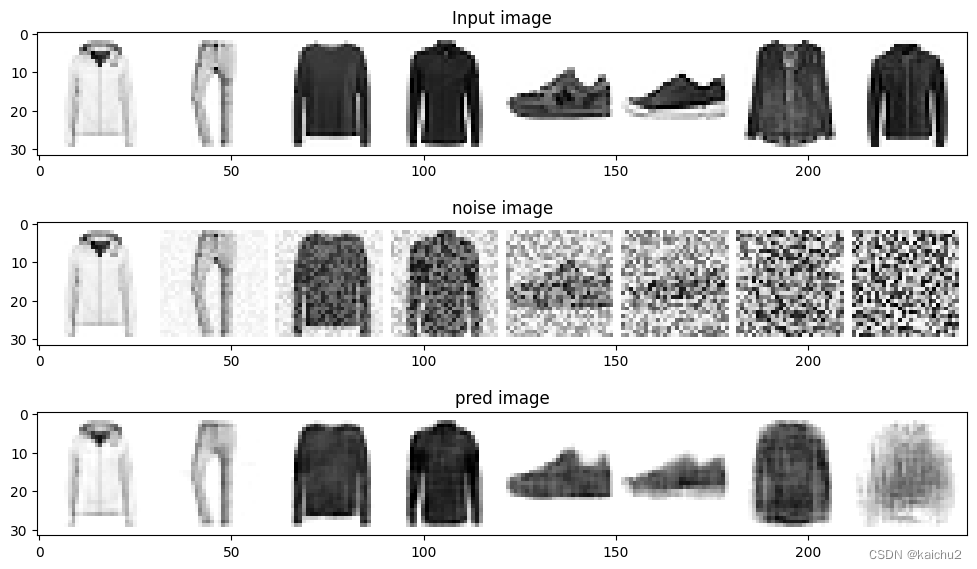
5.7、扩散模型之采样过程
如果模型预测的结果不是很好,如何进行优化?
从完全随机的噪声开始,首先检查一下模型的预测结果,然后只朝着预测方向移动一小部分,例如有一张包含了很多噪声的图像,图中隐藏了一些关于数据结构的信息,可以通过将他们输入到模型中获得
新的预测结果,如果新的预测结果比上一次的预测结果稍微好一些(这一次的输入稍微减少了一些噪声),可以根据这个新的、更好一点的预测结果继续向前迈出一步。
# 采样策略:把采样过程拆分为5步,每次只前进一步
n_steps = 5
x = torch.rand(8,1,28,28).to(device) # 从完全随机的值开始
step_history = [x.detach().cpu()]
pred_output_history = []for i in range(n_steps):with torch.no_grad():pred = net(x)pred_output_history.append(pred.detach().cpu())mix_factor = 1 /(n_steps-i)# 设置朝着预测方向移动多少x = x*(1-mix_factor)+(pred*mix_factor)step_history.append(x.detach().cpu())fig,axs = plt.subplots(n_steps,2,figsize=(9,4),sharex=True)
axs[0,0].set_title("x (model input)")
axs[0,1].set_title("model prediction")
# 可视化每个步骤的结果
for i in range(n_steps):axs[i,0].imshow(torchvision.utils.make_grid(step_history[i])[0].clip(0,1))axs[i,1].imshow(torchvision.utils.make_grid(pred_output_history[i])[0].clip(0,1))# 左边是每个阶段模型输入的可视化结果,右侧是预测的"去噪"(即为去除噪声)后的图像,每一步去除一些噪声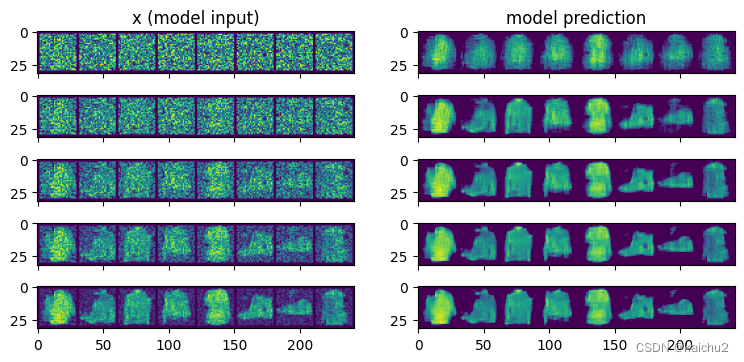
# 将采样过程拆解成40步
n_steps = 40
x = torch.rand(64,1,28,28).to(device)
for i in range(n_steps):# noise_mount = torch.ones((x.shape[0],)).to(device)*(1-(i/n_steps))with torch.no_grad():pred = net(x)mix_factor = 1/(n_steps-i)x = x*(1-mix_factor)+pred*mix_factorfig,ax = plt.subplots(1,1,figsize=(12,12))
ax.imshow(torchvision.utils.make_grid(x.detach().cpu(),nrow=8)[0].clip(0,1))
六、参考链接
- 扩散模型Diffusion Models的原理浅析
- 扩散模型Diffusion Model原理
- What are Diffusion Models? | Lil'Log
相关文章:

扩散模型在图像生成中的应用:从真实样例到逼真图像的奇妙转变
一、扩散模型 扩散模型的起源可以追溯到热力学中的扩散过程。热力学中的扩散过程是指物质从高浓度往低浓度的地方流动,最终达到一种动态的平衡。这个过程就是一个扩散过程。 在深度学习领域中,扩散模型(diffusion models)是深度生…...
Windows 打包 Docker 提示环境错误: no DOCKER_HOST environment variable
这个问题应该还是比较常见的。 [ERROR] Failed to execute goal io.fabric8:docker-maven-plugin:0.40.2:build (default) on project mq-service: Execution default of goal io.fabric8:docker-maven-plugin:0.40.2:build failed: No <dockerHost> given, no DOCKER_H…...
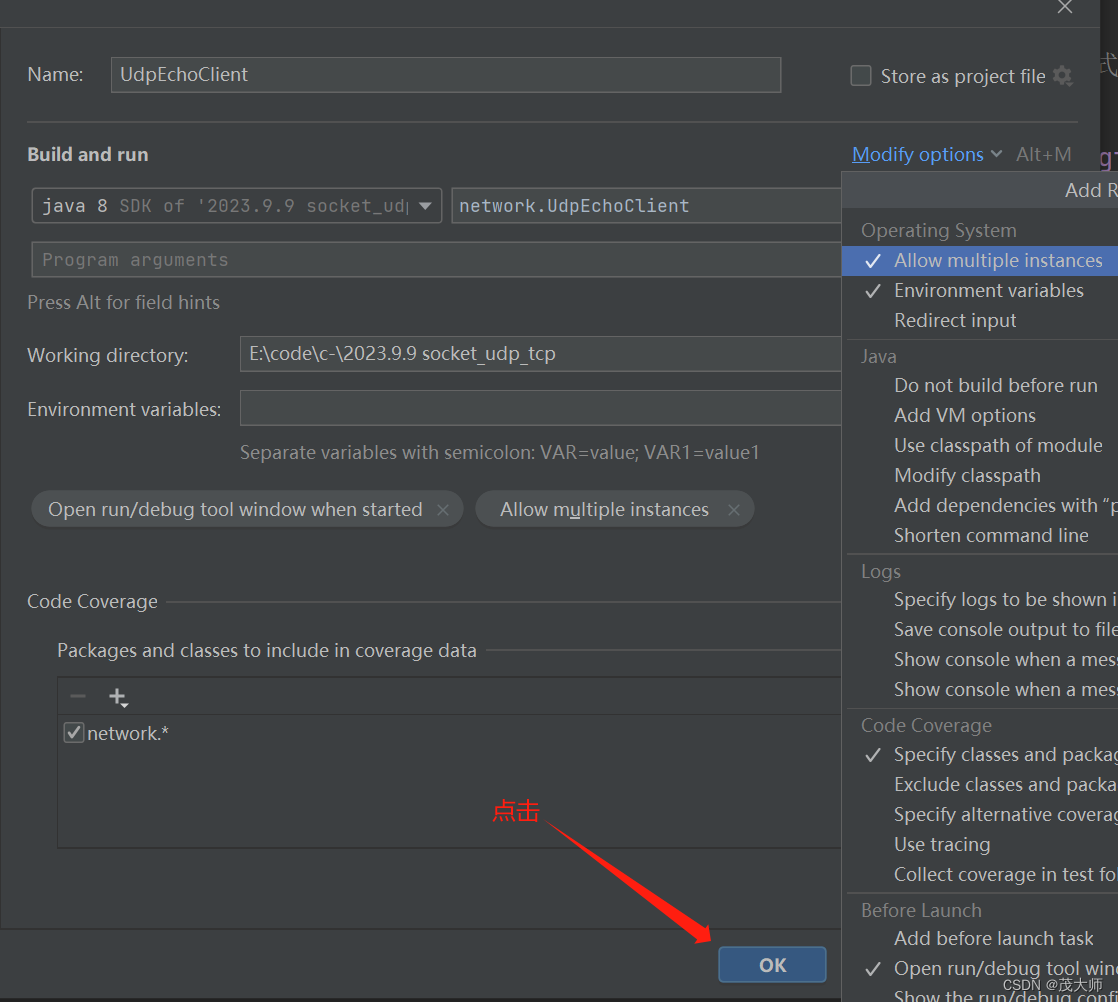
2023.9.8 基于传输层协议 UDP 和 TCP 编写网络通信程序
目录 UDP 基于 UDP 编写网络通信程序 服务器代码 客户端代码 TCP 基于 TCP 编写网络通信程序 服务器代码 客户端代码 IDEA 打开 支持多客户端模式 UDP 特点: 无连接性:发送端和接收端不需要建立连接也可相互通信,且每个 UDP 数据包都…...
)
单例模式,适用于对象唯一的情景(设计模式与开发实践 P4)
文章目录 单例模式实现代理单例惰性单例 上一章后续的内容是关于 JS 函数闭包的,考虑很多读者已经有了闭包基础或者希望通过实战理解,遂跳过上一章直接开始设计模式篇~ 需要注意的是,代码部分仅供参考,主要关注的内容是…...

C语言实现三子棋游戏(详解)
目录 引言: 1.游戏规则: 2.实现步骤: 2.1实现菜单: 2.2创建棋盘并初始化: 2.3绘制棋盘: 2.4玩家落子: 2.5电脑落子: 2.6判断胜负: 3.源码: 结语&…...
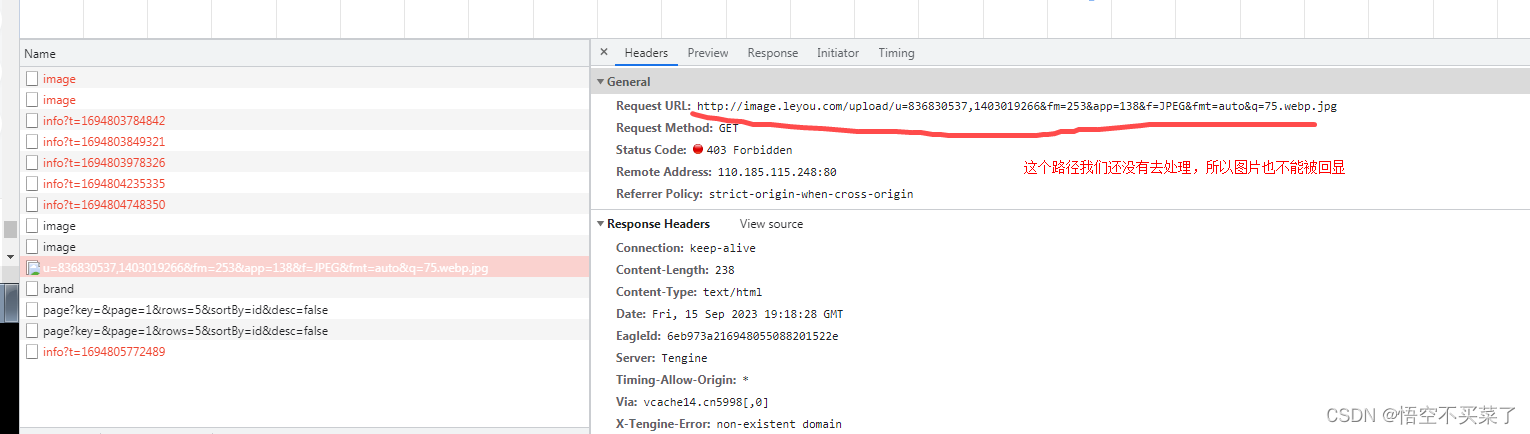
javaee之黑马乐优商城3
异步查询工具axios(儿所以时) vue官方推荐的ajax请求框架 新增品牌页面 如何找到上面这个页面 下面这个页面里面的新增商品弹窗 上面就是请求路径与请求方式 那么请求参数是什么? brand对象,外加商品分类的id数组cids (这里其实不止就是添加…...
 ResNet)
Pytorch intermediate(二) ResNet
实现了残差网络,残差网络结构。代码比之前复杂很多 conv3x3:将输入数据进行一次卷积,将数据转换成为,残差块需要的shape大小 ResidualBlock:残差块,也是所谓的恒等块。为什么被称为恒等块,大概…...

【2023集创赛】加速科技杯作品:高光响应的二硫化铼光电探测器
本文为2023年第七届全国大学生集成电路创新创业大赛(“集创赛”)加速科技杯西北赛区二等奖作品分享,参加极术社区的【有奖征集】分享你的2023集创赛作品,秀出作品风采,分享2023集创赛作品扩大影响力,更有丰…...
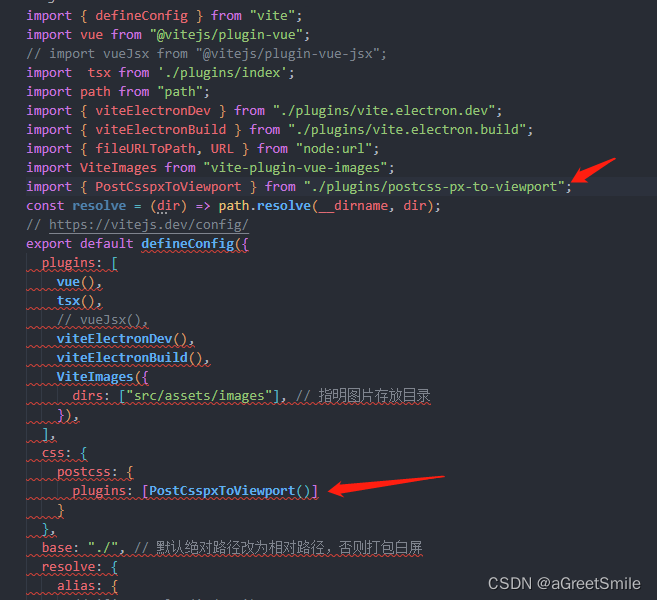
编写postcss插件,全局css文件px转vw
跟目录下创建plugins文件夹,创建postcss-px-to-viewport.ts文件 文件内代码: // postcss 的插件 vite内置了postCss插件 无需安装 import { Plugin } from postcss;interface Options {viewportWidth: number }const Options {viewportWidth: 375, // …...
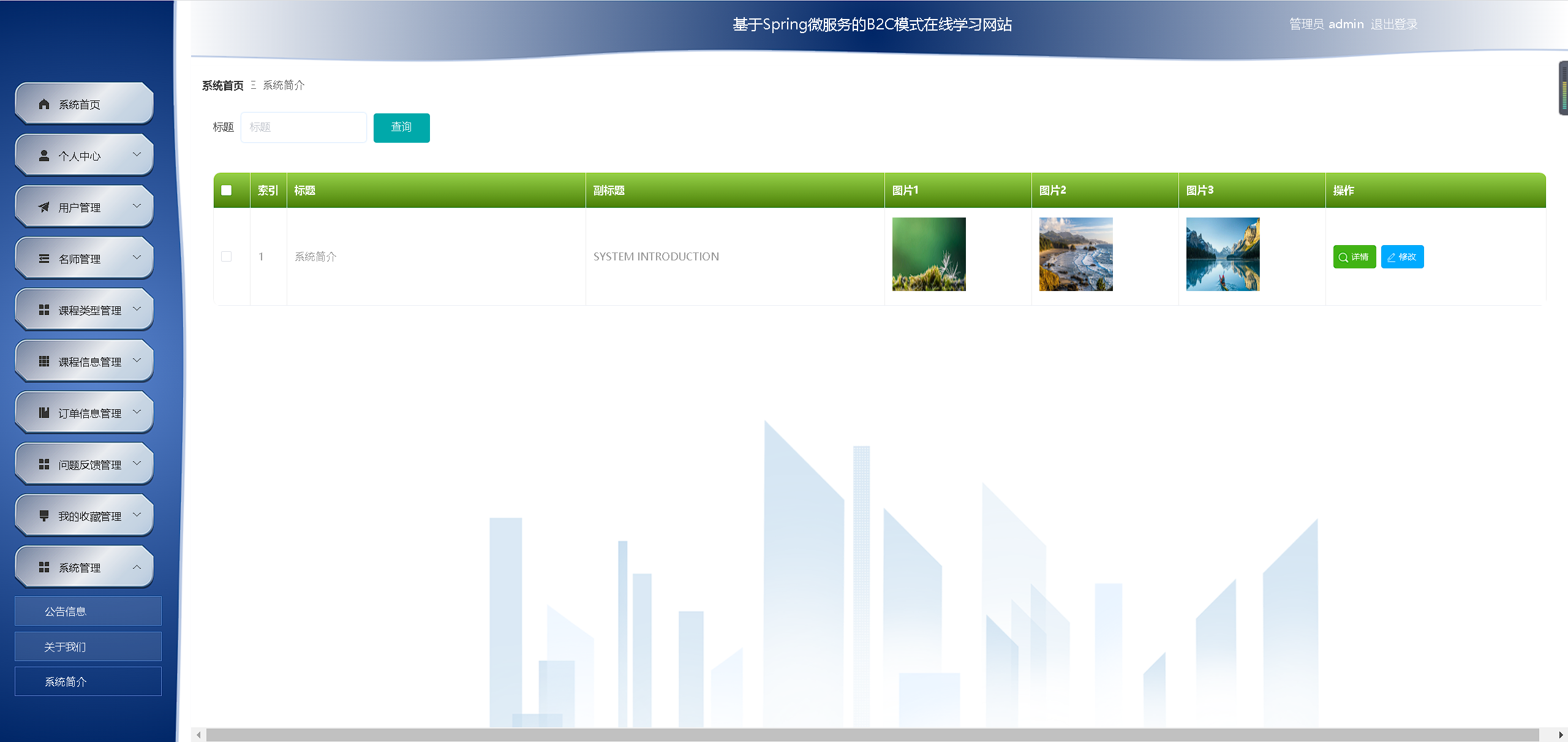
精品SpringCloud的B2C模式在线学习网微服务分布式
《[含文档PPT源码等]精品基于SpringCloud实现的B2C模式在线学习网站-微服务-分布式》该项目含有源码、文档、PPT、配套开发软件、软件安装教程、项目发布教程等 软件开发环境及开发工具: 开发语言:Java 框架:springcloud JDK版本…...
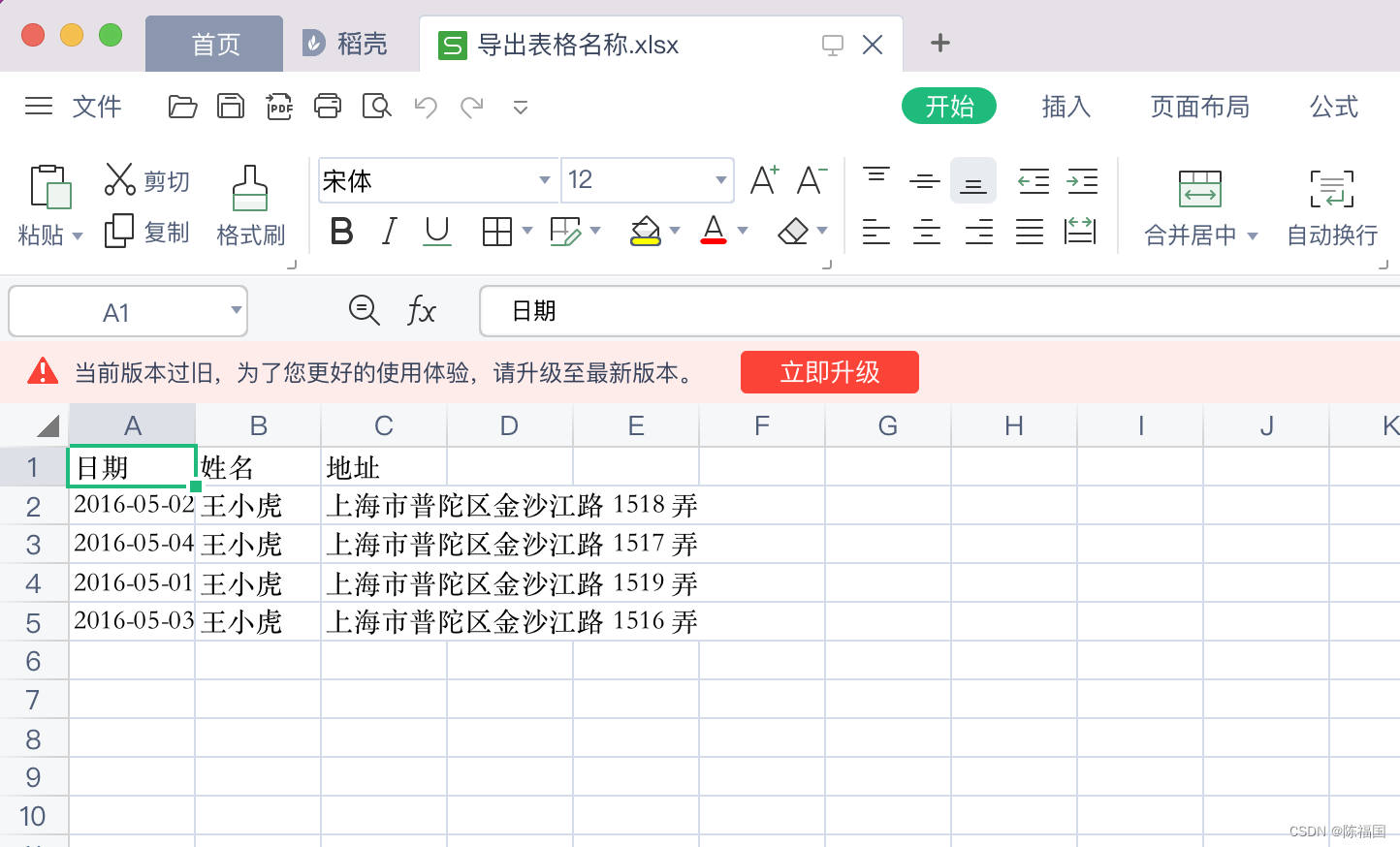
解决vue项目导出当前页Table为Excel
解决vue项目中导出当前页表格为Excel表格的方案 用到的技术: Vue2Element-uifile-saverxlsx 1、创建vue项目,安装element-ui 2、创建一个组件,组件内放入表格,和导出按钮 <template><div><!-- 导出的按钮 -->…...
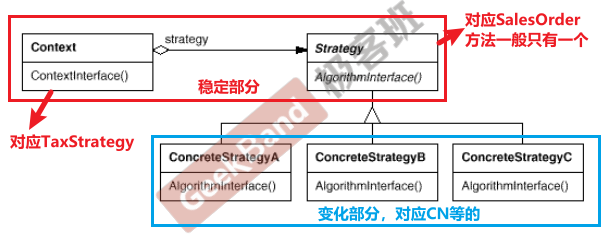
C++设计模式_04_Strategy 策略模式
接上篇,本篇将会介绍C设计模式中的Strategy 策略模式,和上篇模板方法Template Method一样,仍属于“组件协作”模式,它与Template Method有着异曲同工之妙。 文章目录 1. 动机( Motivation)2. 代码演示Stra…...
)
目标检测YOLO实战应用案例100讲-基于YOLOv3多模块融合的遥感目标检测(中)
目录 2.2.3 YOLO 2.3 目标检测算法分析 2.3.1 目标检测结果评价指标...

element 表格fixed列高度无法100%
下文提到的滚动条皆为横向滚动条错误方法(旧方法,点击查看旧博客) 一下代码虽然能解决fixed列高度无法100%问题,但是会出现fixed列下面的滚动条无法被点击的问题(被fixed列遮挡),所以该方法并不…...
【接口自动化测试】Eolink Apilkit 安装部署,支持 Windows、Mac、Linux 等系统
Eolink Apikit 有三种客户端,可以依据自己的情况选择。三种客户端的数据是共用的,因此可以随时切换不同的客户端。 我们推荐使用新推出的 Apikit PC 客户端,PC 端拥有线上产品所有的功能,并且针对本地测试、自动化测试以及使用体…...
解决sass问题:npm ERR! node-sass@9.0.0 postinstall: `node scripts/build.js`
目录 一、遇到问题 解决办法 二、 再次遇到问题 解决办法 题外话 一、遇到问题 1.运行这个项目的适合,遇到了没有sass的问题 解决办法 然后就用命令下载sass npm install node-sass 二、 再次遇到问题 2.下载sass的时候又发现了一个这样的问题 npm ER…...

Python技巧---tqdm库的使用
文章目录 一、tqdm基本知识二、在pytorch中使用tqdm 提示:以下是本篇文章正文内容,下面案例可供参考 一、tqdm基本知识 “tqdm” 是一个 Python 库,用于在命令行界面中创建进度条。 基本使用如下: from tqdm import tqdm impor…...
linux-线程条件变量(cond)
概述 与互斥锁不同,条件变量是用来等待而不是用来上锁的。条件变量用来自动阻塞一个线程,直到某特殊情况发生为止。通常条件变量和互斥锁同时使用 。 条件变量使我们可以睡眠等待某种条件出现。条件变量是利用线程间共享的全局变量进行同步的一种机制&a…...

面试算法6:排序数组中的两个数字之和
题目 输入一个递增排序的数组和一个值k,请问如何在数组中找出两个和为k的数字并返回它们的下标?假设数组中存在且只存在一对符合条件的数字,同时一个数字不能使用两次。例如,输入数组[1,2,4,6&…...

【智能家居-大模型】构建未来,聆思大模型智能家居交互解决方案正式发布
LISTENAI 近日,国内11家大模型陆续通过《生成式人工智能服务管理暂行办法》备案,多家大模型产品已正式开放,激发了新一轮大模型热潮。大模型在自然语言理解方面的巨大突破,实现了认知智能的技术跃迁,带来了时代的智慧…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

视觉slam十四讲实践部分记录——ch2、ch3
ch2 一、使用g++编译.cpp为可执行文件并运行(P30) g++ helloSLAM.cpp ./a.out运行 二、使用cmake编译 mkdir build cd build cmake .. makeCMakeCache.txt 文件仍然指向旧的目录。这表明在源代码目录中可能还存在旧的 CMakeCache.txt 文件,或者在构建过程中仍然引用了旧的路…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
