机器学习练习-决策树
机器学习练习-决策树
代码更新地址:https://github.com/fengdu78/WZU-machine-learning-course
代码修改并注释:黄海广,haiguang2000@wzu.edu.cn
1.分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if-then规则的集合,也可以看作是定义在特征空间划分上的类的条件概率分布。
2.决策树学习旨在构建一个与训练数据拟合很好,并且复杂度小的决策树。因为从可能的决策树中直接选取最优决策树是NP完全问题。现实中采用启发式方法学习次优的决策树。
决策树学习算法包括3部分:特征选择、树的生成和树的剪枝。常用的算法有ID3、
C4.5和CART。
3.特征选择的目的在于选取对训练数据能够分类的特征。特征选择的关键是其准则。常用的准则如下:
(1)样本集合 D D D对特征 A A A的信息增益(ID3)
g ( D , A ) = H ( D ) − H ( D ∣ A ) g(D, A)=H(D)-H(D|A) g(D,A)=H(D)−H(D∣A)
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ H(D)=-\sum_{k=1}^{K} \frac{\left|C_{k}\right|}{|D|} \log _{2} \frac{\left|C_{k}\right|}{|D|} H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) H(D | A)=\sum_{i=1}^{n} \frac{\left|D_{i}\right|}{|D|} H\left(D_{i}\right) H(D∣A)=i=1∑n∣D∣∣Di∣H(Di)
其中, H ( D ) H(D) H(D)是数据集 D D D的熵, H ( D i ) H(D_i) H(Di)是数据集 D i D_i Di的熵, H ( D ∣ A ) H(D|A) H(D∣A)是数据集 D D D对特征 A A A的条件熵。 D i D_i Di是 D D D中特征 A A A取第 i i i个值的样本子集, C k C_k Ck是 D D D中属于第 k k k类的样本子集。 n n n是特征 A A A取 值的个数, K K K是类的个数。
(2)样本集合 D D D对特征 A A A的信息增益比(C4.5)
g R ( D , A ) = g ( D , A ) H ( D ) g_{R}(D, A)=\frac{g(D, A)}{H(D)} gR(D,A)=H(D)g(D,A)
其中, g ( D , A ) g(D,A) g(D,A)是信息增益, H ( D ) H(D) H(D)是数据集 D D D的熵。
(3)样本集合 D D D的基尼指数(CART)
Gini ( D ) = 1 − ∑ k = 1 K ( ∣ C k ∣ ∣ D ∣ ) 2 \operatorname{Gini}(D)=1-\sum_{k=1}^{K}\left(\frac{\left|C_{k}\right|}{|D|}\right)^{2} Gini(D)=1−k=1∑K(∣D∣∣Ck∣)2
特征 A A A条件下集合 D D D的基尼指数:
Gini ( D , A ) = ∣ D 1 ∣ ∣ D ∣ Gini ( D 1 ) + ∣ D 2 ∣ ∣ D ∣ Gini ( D 2 ) \operatorname{Gini}(D, A)=\frac{\left|D_{1}\right|}{|D|} \operatorname{Gini}\left(D_{1}\right)+\frac{\left|D_{2}\right|}{|D|} \operatorname{Gini}\left(D_{2}\right) Gini(D,A)=∣D∣∣D1∣Gini(D1)+∣D∣∣D2∣Gini(D2)
4.决策树的生成。通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标,从根结点开始,递归地产生决策树。这相当于用信息增益或其他准则不断地选取局部最优的特征,或将训练集分割为能够基本正确分类的子集。
5.决策树的剪枝。由于生成的决策树存在过拟合问题,需要对它进行剪枝,以简化学到的决策树。决策树的剪枝,往往从已生成的树上剪掉一些叶结点或叶结点以上的子树,并将其父结点或根结点作为新的叶结点,从而简化生成的决策树。
导入包:
import numpy as np
import pandas as pd
import math
from math import log
创建数据
def create_data():datasets = [['青年', '否', '否', '一般', '否'],['青年', '否', '否', '好', '否'],['青年', '是', '否', '好', '是'],['青年', '是', '是', '一般', '是'],['青年', '否', '否', '一般', '否'],['中年', '否', '否', '一般', '否'],['中年', '否', '否', '好', '否'],['中年', '是', '是', '好', '是'],['中年', '否', '是', '非常好', '是'],['中年', '否', '是', '非常好', '是'],['老年', '否', '是', '非常好', '是'],['老年', '否', '是', '好', '是'],['老年', '是', '否', '好', '是'],['老年', '是', '否', '非常好', '是'],['老年', '否', '否', '一般', '否'],]labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别']# 返回数据集和每个维度的名称return datasets, labels
datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
train_data
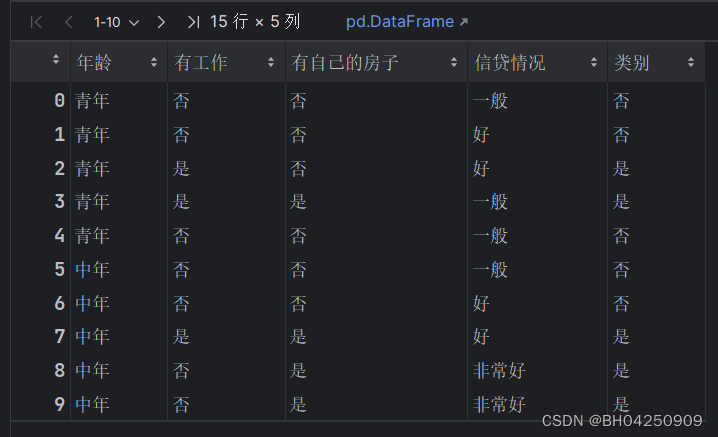
熵
# 计算给定数据集的熵(信息熵)
def calc_ent(datasets):# 计算数据集的长度data_length = len(datasets)# 统计数据集中每个类别的出现次数label_count = {}for i in range(data_length):# 获取每个样本的标签label = datasets[i][-1]# 如果该类别不在label_count中,则添加到label_count中if label not in label_count:label_count[label] = 0# 统计该类别的出现次数label_count[label] += 1# 计算熵ent = -sum([(p / data_length) * log(p / data_length, 2)for p in label_count.values()])return ent
条件熵
# 计算给定数据集在指定特征上的条件熵
def cond_ent(datasets, axis=0):# 计算数据集的长度data_length = len(datasets)# 使用字典feature_sets存储在指定特征上的不同取值对应的样本集合feature_sets = {}for i in range(data_length):# 获取每个样本在指定特征上的取值feature = datasets[i][axis]# 如果该取值不在feature_sets中,则添加到feature_sets中if feature not in feature_sets:feature_sets[feature] = []# 将该样本添加到对应取值的样本集合中feature_sets[feature].append(datasets[i])# 计算条件熵cond_ent = sum([(len(p) / data_length) * calc_ent(p)for p in feature_sets.values()])return cond_ent
calc_ent(datasets)
0.9709505944546686
信息增益
#计算信息增益
def info_gain(ent, cond_ent):# 信息增益等于熵减去条件熵return ent - cond_ent
#使用信息增益选择最佳特征作为根节点特征进行决策树的训练
def info_gain_train(datasets):# 计算特征的数量count = len(datasets[0]) - 1# 计算整个数据集的熵ent = calc_ent(datasets)# 存储每个特征的信息增益best_feature = []for c in range(count):# 计算每个特征的条件熵c_info_gain = info_gain(ent, cond_ent(datasets, axis=c))# 将特征及其对应的信息增益存入best_feature列表中best_feature.append((c, c_info_gain))# 输出每个特征的信息增益print('特征({}) 的信息增益为: {:.3f}'.format(labels[c], c_info_gain))# 找到信息增益最大的特征best_ = max(best_feature, key=lambda x: x[-1])# 返回信息增益最大的特征作为根节点特征return '特征({})的信息增益最大,选择为根节点特征'.format(labels[best_[0]])
info_gain_train(np.array(datasets))
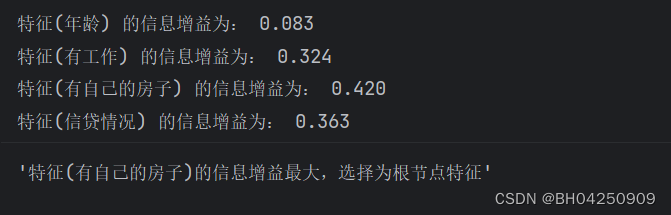
利用ID3算法生成决策树
# 定义节点类 二叉树
class Node:def __init__(self, root=True, label=None, feature_name=None, feature=None):self.root = rootself.label = labelself.feature_name = feature_nameself.feature = featureself.tree = {}self.result = {'label:': self.label,'feature': self.feature,'tree': self.tree}def __repr__(self):return '{}'.format(self.result)def add_node(self, val, node):self.tree[val] = nodedef predict(self, features):if self.root is True:return self.labelreturn self.tree[features[self.feature]].predict(features)class DTree:def __init__(self, epsilon=0.1):self.epsilon = epsilonself._tree = {}# 熵@staticmethoddef calc_ent(datasets):data_length = len(datasets)label_count = {}for i in range(data_length):label = datasets[i][-1]if label not in label_count:label_count[label] = 0label_count[label] += 1ent = -sum([(p / data_length) * log(p / data_length, 2)for p in label_count.values()])return ent# 经验条件熵def cond_ent(self, datasets, axis=0):data_length = len(datasets)feature_sets = {}for i in range(data_length):feature = datasets[i][axis]if feature not in feature_sets:feature_sets[feature] = []feature_sets[feature].append(datasets[i])cond_ent = sum([(len(p) / data_length) * self.calc_ent(p)for p in feature_sets.values()])return cond_ent# 信息增益@staticmethoddef info_gain(ent, cond_ent):return ent - cond_entdef info_gain_train(self, datasets):count = len(datasets[0]) - 1ent = self.calc_ent(datasets)best_feature = []for c in range(count):c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c))best_feature.append((c, c_info_gain))# 比较大小best_ = max(best_feature, key=lambda x: x[-1])return best_def train(self, train_data):"""input:数据集D(DataFrame格式),特征集A,阈值etaoutput:决策树T"""_, y_train, features = train_data.iloc[:, :-1], train_data.iloc[:,-1], train_data.columns[:-1]# 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回Tif len(y_train.value_counts()) == 1:return Node(root=True, label=y_train.iloc[0])# 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回Tif len(features) == 0:return Node(root=True,label=y_train.value_counts().sort_values(ascending=False).index[0])# 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征max_feature, max_info_gain = self.info_gain_train(np.array(train_data))max_feature_name = features[max_feature]# 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返回Tif max_info_gain < self.epsilon:return Node(root=True,label=y_train.value_counts().sort_values(ascending=False).index[0])# 5,构建Ag子集node_tree = Node(root=False, feature_name=max_feature_name, feature=max_feature)feature_list = train_data[max_feature_name].value_counts().indexfor f in feature_list:sub_train_df = train_data.loc[train_data[max_feature_name] ==f].drop([max_feature_name], axis=1)# 6, 递归生成树sub_tree = self.train(sub_train_df)node_tree.add_node(f, sub_tree)# pprint.pprint(node_tree.tree)return node_treedef fit(self, train_data):self._tree = self.train(train_data)return self._treedef predict(self, X_test):return self._tree.predict(X_test)
datasets, labels = create_data()
data_df = pd.DataFrame(datasets, columns=labels)
dt = DTree()
tree = dt.fit(data_df)
tree
{‘label:’: None, ‘feature’: 2, ‘tree’: {‘否’: {‘label:’: None, ‘feature’: 1, ‘tree’: {‘否’: {‘label:’: ‘否’, ‘feature’: None, ‘tree’: {}}, ‘是’: {‘label:’: ‘是’, ‘feature’: None, ‘tree’: {}}}}, ‘是’: {‘label:’: ‘是’, ‘feature’: None, ‘tree’: {}}}}
dt.predict(['老年', '否', '否', '一般'])
‘否’
Scikit-learn实例
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
使用Iris数据集,我们可以构建如下树:
#data
def create_data():iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df['label'] = iris.targetdf.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']data = np.array(df.iloc[:100, [0, 1, -1]])# print(data)return data[:, :2], data[:, -1],iris.feature_names[0:2]X, y,feature_name= create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
决策树分类
from sklearn.tree import DecisionTreeClassifier
from sklearn.tree import export_graphviz
import graphviz
from sklearn import treeclf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)clf.score(X_test, y_test)
0.9
一旦经过训练,就可以用 plot_tree函数绘制树:
tree.plot_tree(clf)
[Text(0.5, 0.9, ‘x[0] <= 5.45\ngini = 0.496\nsamples = 70\nvalue = [38, 32]’),
Text(0.25, 0.7, ‘x[1] <= 2.65\ngini = 0.184\nsamples = 39\nvalue = [35, 4]’),
Text(0.125, 0.5, ‘gini = 0.0\nsamples = 3\nvalue = [0, 3]’),
Text(0.375, 0.5, ‘x[0] <= 5.35\ngini = 0.054\nsamples = 36\nvalue = [35, 1]’),
Text(0.25, 0.3, ‘gini = 0.0\nsamples = 30\nvalue = [30, 0]’),
Text(0.5, 0.3, ‘x[1] <= 3.2\ngini = 0.278\nsamples = 6\nvalue = [5, 1]’),
Text(0.375, 0.1, ‘gini = 0.0\nsamples = 1\nvalue = [0, 1]’),
Text(0.625, 0.1, ‘gini = 0.0\nsamples = 5\nvalue = [5, 0]’),
Text(0.75, 0.7, ‘x[1] <= 3.6\ngini = 0.175\nsamples = 31\nvalue = [3, 28]’),
Text(0.625, 0.5, ‘gini = 0.0\nsamples = 28\nvalue = [0, 28]’),
Text(0.875, 0.5, ‘gini = 0.0\nsamples = 3\nvalue = [3, 0]’)]

也可以导出树
tree_pic = export_graphviz(clf, out_file="mytree.pdf")
with open('mytree.pdf') as f:dot_graph = f.read()
graphviz.Source(dot_graph)
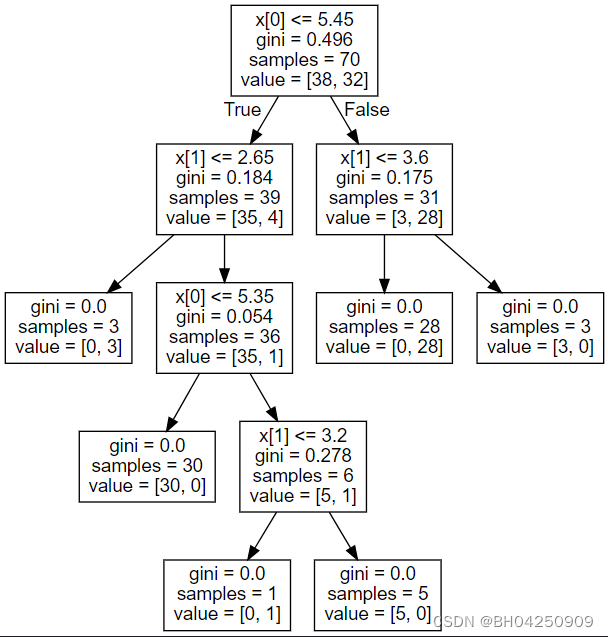
或者,还可以使用函数 export_text以文本格式导出树。此方法不需要安装外部库,而且更紧凑:
from sklearn.tree import export_text
r = export_text(clf)
print(r)
|— feature_0 <= 5.45
| |— feature_1 <= 2.65
| | |— class: 1.0
| |— feature_1 > 2.65
| | |— feature_0 <= 5.35
| | | |— class: 0.0
| | |— feature_0 > 5.35
| | | |— feature_1 <= 3.20
| | | | |— class: 1.0
| | | |— feature_1 > 3.20
| | | | |— class: 0.0
|— feature_0 > 5.45
| |— feature_1 <= 3.60
| | |— class: 1.0
| |— feature_1 > 3.60
| | |— class: 0.0
决策树回归
import numpy as np
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
# Create a random dataset
rng = np.random.RandomState(1)
X = np.sort(5 * rng.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - rng.rand(16))
# Fit regression model
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)# Predict
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)# Plot the results
plt.figure()
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.plot(X_test, y_1, color="cornflowerblue", label="max_depth=2", linewidth=2)
plt.plot(X_test, y_2, color="yellowgreen", label="max_depth=5", linewidth=2)
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
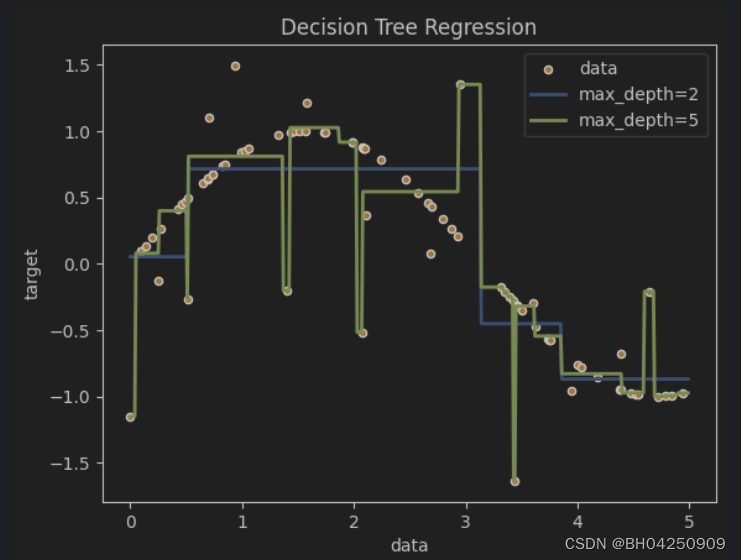
Scikit-learn 的决策树参数
DecisionTreeClassifier(criterion=“gini”,
splitter=“best”,
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
min_weight_fraction_leaf=0.,
max_features=None,
random_state=None,
max_leaf_nodes=None,
min_impurity_decrease=0.,
min_impurity_split=None,
class_weight=None,
presort=False)
参数含义:
1.criterion:string, optional (default=“gini”)
(1).criterion=‘gini’,分裂节点时评价准则是Gini指数。
(2).criterion=‘entropy’,分裂节点时的评价指标是信息增益。
2.max_depth:int or None, optional (default=None)。指定树的最大深度。
如果为None,表示树的深度不限。直到所有的叶子节点都是纯净的,即叶子节点
中所有的样本点都属于同一个类别。或者每个叶子节点包含的样本数小于min_samples_split。
3.splitter:string, optional (default=“best”)。指定分裂节点时的策略。
(1).splitter=‘best’,表示选择最优的分裂策略。
(2).splitter=‘random’,表示选择最好的随机切分策略。
4.min_samples_split:int, float, optional (default=2)。表示分裂一个内部节点需要的做少样本数。
(1).如果为整数,则min_samples_split就是最少样本数。
(2).如果为浮点数(0到1之间),则每次分裂最少样本数为ceil(min_samples_split * n_samples)
5.min_samples_leaf: int, float, optional (default=1)。指定每个叶子节点需要的最少样本数。
(1).如果为整数,则min_samples_split就是最少样本数。
(2).如果为浮点数(0到1之间),则每个叶子节点最少样本数为ceil(min_samples_leaf * n_samples)
6.min_weight_fraction_leaf:float, optional (default=0.)
指定叶子节点中样本的最小权重。
7.max_features:int, float, string or None, optional (default=None).
搜寻最佳划分的时候考虑的特征数量。
(1).如果为整数,每次分裂只考虑max_features个特征。
(2).如果为浮点数(0到1之间),每次切分只考虑int(max_features * n_features)个特征。
(3).如果为’auto’或者’sqrt’,则每次切分只考虑sqrt(n_features)个特征
(4).如果为’log2’,则每次切分只考虑log2(n_features)个特征。
(5).如果为None,则每次切分考虑n_features个特征。
(6).如果已经考虑了max_features个特征,但还是没有找到一个有效的切分,那么还会继续寻找
下一个特征,直到找到一个有效的切分为止。
8.random_state:int, RandomState instance or None, optional (default=None)
(1).如果为整数,则它指定了随机数生成器的种子。
(2).如果为RandomState实例,则指定了随机数生成器。
(3).如果为None,则使用默认的随机数生成器。
9.max_leaf_nodes: int or None, optional (default=None)。指定了叶子节点的最大数量。
(1).如果为None,叶子节点数量不限。
(2).如果为整数,则max_depth被忽略。
10.min_impurity_decrease:float, optional (default=0.)
如果节点的分裂导致不纯度的减少(分裂后样本比分裂前更加纯净)大于或等于min_impurity_decrease,则分裂该节点。
加权不纯度的减少量计算公式为:
min_impurity_decrease=N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
其中N是样本的总数,N_t是当前节点的样本数,N_t_L是分裂后左子节点的样本数,
N_t_R是分裂后右子节点的样本数。impurity指当前节点的基尼指数,right_impurity指
分裂后右子节点的基尼指数。left_impurity指分裂后左子节点的基尼指数。
11.min_impurity_split:float
树生长过程中早停止的阈值。如果当前节点的不纯度高于阈值,节点将分裂,否则它是叶子节点。
这个参数已经被弃用。用min_impurity_decrease代替了min_impurity_split。
12.class_weight:dict, list of dicts, “balanced” or None, default=None
类别权重的形式为{class_label: weight}
(1).如果没有给出每个类别的权重,则每个类别的权重都为1。
(2).如果class_weight=‘balanced’,则分类的权重与样本中每个类别出现的频率成反比。
计算公式为:n_samples / (n_classes * np.bincount(y))
(3).如果sample_weight提供了样本权重(由fit方法提供),则这些权重都会乘以sample_weight。
13.presort:bool, optional (default=False)
指定是否需要提前排序数据从而加速训练中寻找最优切分的过程。设置为True时,对于大数据集
会减慢总体的训练过程;但是对于一个小数据集或者设定了最大深度的情况下,会加速训练过程。
决策树调参
# 导入库
from sklearn.tree import DecisionTreeClassifier
from sklearn import datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor
from sklearn import metrics
# 导入数据集
X = datasets.load_iris() # 以全部字典形式返回,有data,target,target_names三个键
data = X.data
target = X.target
name = X.target_names
x, y = datasets.load_iris(return_X_y=True) # 能一次性取前2个
print(x.shape, y.shape)
(150, 4) (150,)
# 数据分为训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x,y,test_size=0.2,random_state=100)
# 用GridSearchCV寻找最优参数(字典)
param = {'criterion': ['gini'],'max_depth': [30, 50, 60, 100],'min_samples_leaf': [2, 3, 5, 10],'min_impurity_decrease': [0.1, 0.2, 0.5]
}
grid = GridSearchCV(DecisionTreeClassifier(), param_grid=param, cv=6)
grid.fit(x_train, y_train)
print('最优分类器:', grid.best_params_, '最优分数:', grid.best_score_) # 得到最优的参数和分值
最优分类器: {‘criterion’: ‘gini’, ‘max_depth’: 50, ‘min_impurity_decrease’: 0.2, ‘min_samples_leaf’: 2} 最优分数: 0.9416666666666665
参考:
https://github.com/fengdu78/lihang-code
李航. 统计学习方法[M]. 北京: 清华大学出版社,2019.
https://scikit-learn.org
相关文章:

机器学习练习-决策树
机器学习练习-决策树 代码更新地址:https://github.com/fengdu78/WZU-machine-learning-course 代码修改并注释:黄海广,haiguang2000wzu.edu.cn 1.分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if…...
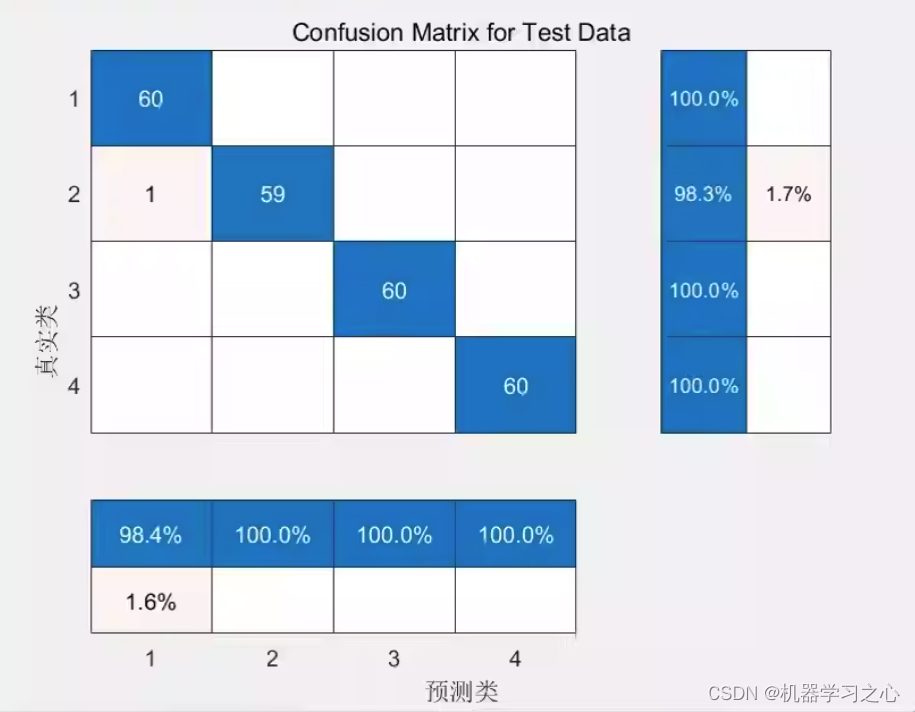
分类预测 | Matlab实现基于LFDA-SVM局部费歇尔判别数据降维结合支持向量机的多输入分类预测
分类预测 | Matlab实现基于LFDA-SVM局部费歇尔判别数据降维结合支持向量机的多输入分类预测 目录 分类预测 | Matlab实现基于LFDA-SVM局部费歇尔判别数据降维结合支持向量机的多输入分类预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 基于局部费歇尔判别数据降维的L…...
Say0l的安全开发-代理扫描工具-Sayo-proxyscan【红队工具】
写在前面 终于终于,安全开发也练习一年半了,有时间完善一下项目,写写中间踩过的坑。 安全开发的系列全部都会上传至github,欢迎使用和star。 工具链接地址 https://github.com/SAY0l/Sayo-proxyscan 工具简介 SOCKS4/SOCKS4…...

使用FFmpeg+ubuntu系统转化flac无损音频为mp3
功能需求如上题,我们来具体的操作一下: 1.先在ubuntu上面安装FFmpeg:sudo apt install ffmpeg 2.进入有flac音频文件的目录使用下述命令: ffmpeg -i test.FLAC -c:a libmp3lame -q:a 2 output.mp3 3.如果没有什么意外的话,你就能看到你的文件夹里面已经有转化好的mp3文件了 批…...

I/O多路复用三种实现
一.select 实现 (1)select流程 基本流程是: 1. 先构造一张有关文件描述符的表; fd_set readfds 2. 清空表 FD_ZERO() 3. 将你关心的文件描述符加入到这…...

DataInputStream数据读取 Vs ByteBuffer数据读取的巨大性能差距
背景: 今天在查找一个序列化和反序列化相关的问题时,意外发现使用DataInputStream读取和ByteBuffer读取之间性能相差巨大,本文就来记录下这两者在读取整数类型时的性能差异,以便在平时使用的过程中引起注意 DataInputStream数据…...

org.apache.flink.table.api.TableException: Sink does not exists
FlinkSQL_1.12_用DDL实现Kafka到MySQL的数据传输_实现按照条件进行过滤写入MySQL_flink从kafka拉取数据并过滤数据写入mysql_旧城里的阳光的博客-CSDN博客 参考这篇文章,写了kafka到mysql的代码例子,因为自己改了表结构,运行下面代码&#x…...
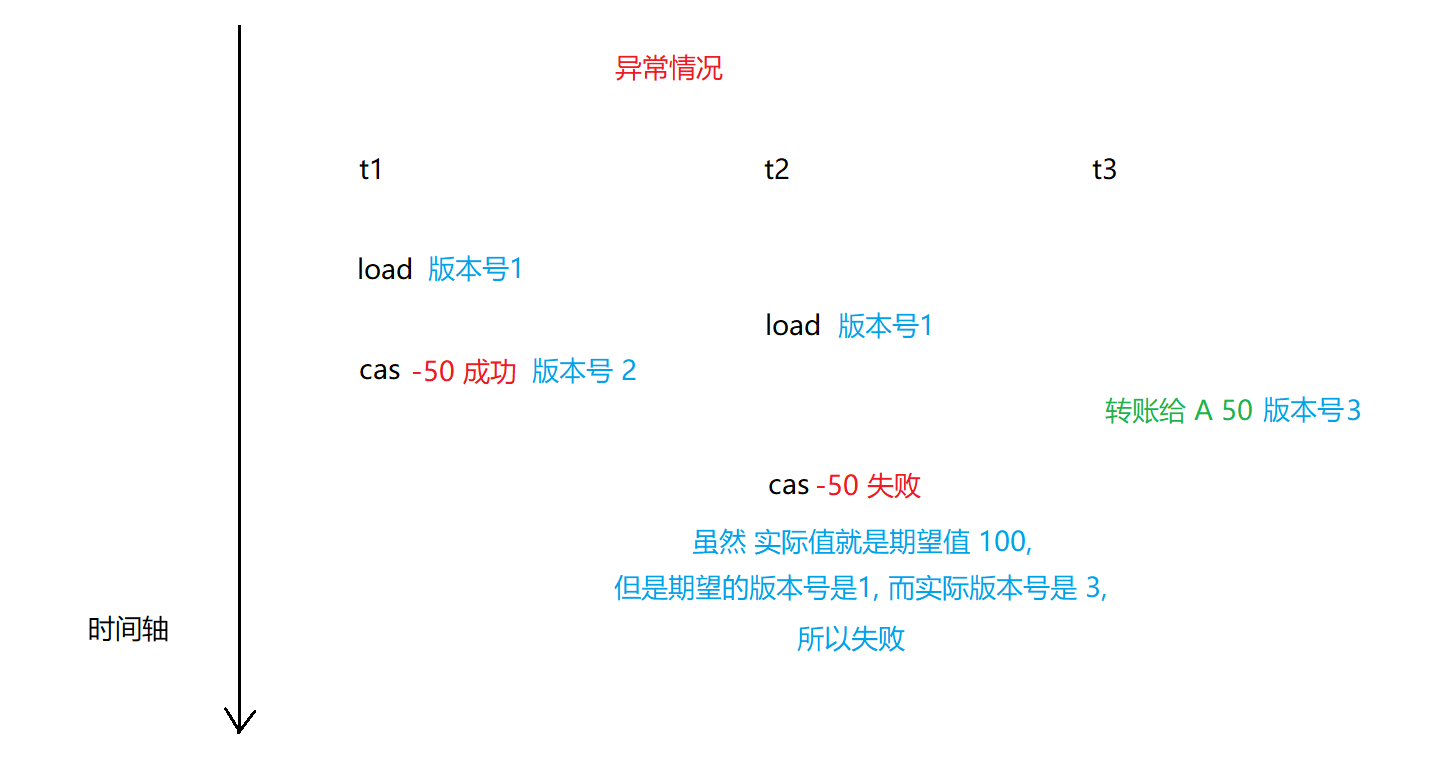
【多线程】CAS 详解
CAS 详解 一. 什么是 CAS二. CAS 的应用1. 实现原子类2. 实现自旋锁 三. CAS 的 ABA 问题四. 相关面试题 一. 什么是 CAS CAS: 全称Compare and swap,字面意思:”比较并交换“一个 CAS 涉及到以下操作: 我们假设内存中的原数据 V,旧的预期值…...

卷积神经网络实现咖啡豆分类 - P7
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制🚀 文章来源:K同学的学习圈子 目录 环境步骤环境设置包引用全局设备对象 数据准备查看图像的信息制作数据集 模型设…...

C++之默认与自定义构造函数问题(二百一十七)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...
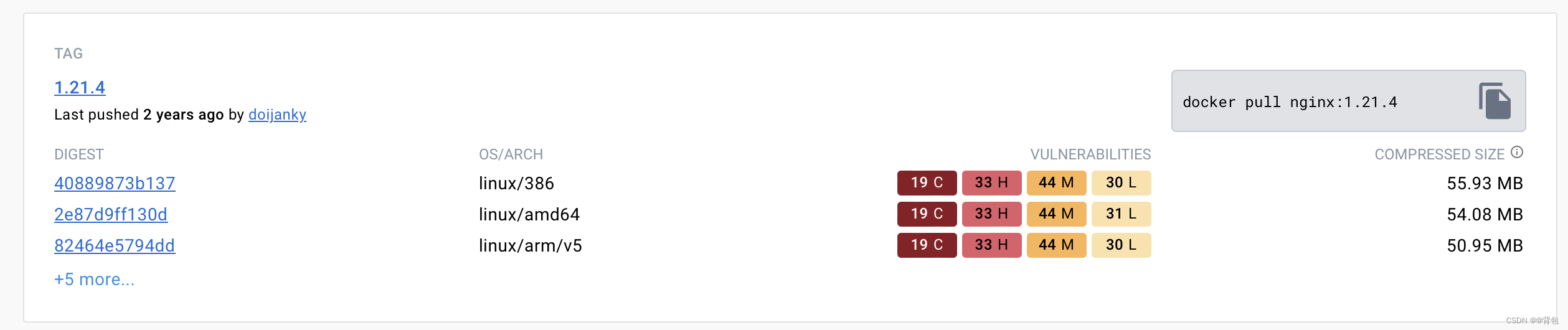
Docker从认识到实践再到底层原理(五)|Docker镜像
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...

【Flowable】任务监听器(五)
前言 之前有需要使用到Flowable,鉴于网上的资料不是很多也不是很全也是捣鼓了半天,因此争取能在这里简单分享一下经验,帮助有需要的朋友,也非常欢迎大家指出不足的地方。 一、监听器 在Flowable中,我们可以使用监听…...

spring-kafka中ContainerProperties.AckMode详解
近期,我们线上遇到了一个性能问题,几乎快引起线上故障,后来仅仅是修改了一行代码,性能就提升了几十倍。一行代码几十倍,数据听起来很夸张,不过这是真实的数据,线上错误的配置的确有可能导致性能…...
)
【rpc】Dubbo和Zookeeper结合使用,它们的作用与联系(通俗易懂,一文理解)
目录 Dubbo是什么? 把系统模块变成分布式,有哪些好处,本来能在一台机子上运行,为什么还要远程调用 Zookeeper是什么? 它们进行配合使用时,之间的关系 服务注册 服务发现 动态地址管理 Dubbo是…...

ChatGPT的未来
随着人工智能的快速发展,ChatGPT作为一种自然语言生成模型,在各个领域都展现出了巨大的潜力。它不仅可以用于日常对话、创意助手和知识查询,还可以应用于教育、医疗、商业等各个领域,为人们带来更多便利和创新。 在教育领域&#…...

Pytorch模型转ONNX部署
开始以为会很困难,但是其实非常方便,下边分两步走:1. pytorch模型转onnx;2. 使用onnx进行inference 0. 准备工作 0.1 安装onnx 安装onnx和onnxruntime,onnx貌似是个环境。。倒是没有直接使用,onnxruntim…...

k8s优雅停服
在应用程序的整个生命周期中,正在运行的 pod 会由于多种原因而终止。在某些情况下,Kubernetes 会因用户输入(例如更新或删除 Deployment 时)而终止 pod。在其他情况下,Kubernetes 需要释放给定节点上的资源时会终止 po…...

面试题五:computed的使用
题记 大部分的工作中使用computed的频次很低的,所以今天拿出来一文对于computed进行详细的介绍,因为Vue的灵魂之一就是computed。 模板内的表达式非常便利,但是设计它们的初衷是用于简单运算的。在模板中放入太多的逻辑会让模板过重且难以维护…...
完美的分布式监控系统 Prometheus与优雅的开源可视化平台 Grafana
1、之间的关系 prometheus与grafana之间是相辅相成的关系。简而言之Grafana作为可视化的平台,平台的数据从Prometheus中取到来进行仪表盘的展示。而Prometheus这源源不断的给Grafana提供数据的支持。 Prometheus是一个开源的系统监控和报警系统,能够监…...
黑马JVM总结(九)
(1)StringTable_调优1 我们知道StringTable底层是一个哈希表,哈希表的性能是跟它的大小相关的,如果哈希表这个桶的个数比较多,元素相对分散,哈希碰撞的几率就会减少,查找的速度较快,…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
