数学基础整理
收纳一些天天忘的结论qwq
线性求逆元
- invi=(p−pi)×invpmodiinv_i=(p-\dfrac{p}{i})\times inv_{p\bmod i}invi=(p−ip)×invpmodi
卡特兰数
-
组合数公式:Hn=C2nn−C2nn−1H_n=C_{2n}^n-C_{2n}^{n-1}Hn=C2nn−C2nn−1
-
递推式:Hn=Hn−1(4n−2)n+1H_n=\dfrac{H_{n-1}(4n-2)}{n+1}Hn=n+1Hn−1(4n−2)
欧拉函数
-
n=∑d∣nφ(d)n=\sum\limits_{d\mid n} \varphi(d)n=d∣n∑φ(d)
-
欧拉定理:gcd(a,m)=1,aφ(m)≡1(modm)\gcd(a,m)=1,a^{\varphi(m)}\equiv1\pmod mgcd(a,m)=1,aφ(m)≡1(modm)
-
拓展欧拉定理:ab≡{abmodφ(m)gcd(a,m)=1abgcd(a,m)≠1∧b<φ(m)abmodφ(m)+φ(m)gcd(a,m)≠1∧b≥φ(m)a^b\equiv\begin{cases}a^{b\bmod \varphi(m)}\quad \gcd(a,m)=1\\ a^b\quad \gcd(a,m)\ne 1\land b<\varphi(m)\\ a^{b\bmod \varphi(m)+\varphi(m)}\quad \gcd(a,m)\ne 1\land b\ge \varphi(m)\end{cases}ab≡⎩⎨⎧abmodφ(m)gcd(a,m)=1abgcd(a,m)=1∧b<φ(m)abmodφ(m)+φ(m)gcd(a,m)=1∧b≥φ(m)(modm)\pmod m(modm)
数论分块
- 满足 ⌊ni⌋=⌊nx⌋\left\lfloor\dfrac{n}{i}\right\rfloor=\left\lfloor\dfrac{n}{x}\right\rfloor⌊in⌋=⌊xn⌋ 的最大 xxx 等于 ⌊n⌊ni⌋⌋\left\lfloor\dfrac{n}{\left\lfloor\frac{n}{i}\right\rfloor}\right\rfloor⌊⌊in⌋n⌋
莫比乌斯变换
- 两个数论函数 f(n),g(n)f(n),g(n)f(n),g(n),若 f(n)=∑d∣ng(d)f(n)=\sum\limits_{d\mid n} g(d)f(n)=d∣n∑g(d),则 g(n)=∑d∣nf(d)μ(nd)g(n)=\sum\limits_{d\mid n} f(d)\mu(\dfrac{n}{d})g(n)=d∣n∑f(d)μ(dn)
阶
使得 an≡1(modm)a^n\equiv1\pmod{m}an≡1(modm) 成立的最小正整数 nnn 叫做 aaa 模 mmm 的阶,符号 δm(a)\delta_m(a)δm(a)。
一些性质:
- ∀an≡1(modm),δm(a)∣n⟹δm(a)∣ϕ(m)\forall a^n\equiv 1\pmod{m},\delta_m(a)\mid n\implies\delta_m(a)\mid\phi(m)∀an≡1(modm),δm(a)∣n⟹δm(a)∣ϕ(m)
- ∀i,j∈[1,δm(a)],i≠jai≢aj(modm)\forall_{i,j\in[1,\delta_m(a)],i\ne j}\ a^i\not\equiv a^j\pmod{m}∀i,j∈[1,δm(a)],i=j ai≡aj(modm)
- gcd(a,m)=1,δm(ak)=δm(a)gcd(k,δm(a))\gcd(a,m)=1,\delta_m(a^k)=\dfrac{\delta_m(a)}{\gcd(k,\delta_m(a))}gcd(a,m)=1,δm(ak)=gcd(k,δm(a))δm(a)
原根
若 gcd(a,m)=1,δm(a)=ϕ(m)\gcd(a,m)=1,\delta_m(a)=\phi(m)gcd(a,m)=1,δm(a)=ϕ(m),则 aaa 是 mmm 的原根。
- 判定定理:∀p∣ϕ(m)aϕ(m)p≢1(modm)⟺a\forall_{p\mid \phi(m)} a^{\frac{\phi(m)}{p}}\not\equiv1\pmod{m}\iff a∀p∣ϕ(m)apϕ(m)≡1(modm)⟺a 是 mmm 的原根;
- 存在定理:只有 2,4,pa,2pa2,4,p^a,2p^a2,4,pa,2pa 才存在原根,其中 ppp 为奇素数;
- 原根个数:若 mmm 有原根,则其原根个数为 ϕ(ϕ(m))\phi(\phi(m))ϕ(ϕ(m));
- mmm 的最小原根 ggg 不超过 m14m^{\frac{1}{4}}m41,所有其它原根均为 gk(gcd(k,ϕ(m)=1))g^k\ (\gcd(k,\phi(m)=1))gk (gcd(k,ϕ(m)=1))。
相关文章:

数学基础整理
收纳一些天天忘的结论qwq 线性求逆元 invi(p−pi)invpmodiinv_i(p-\dfrac{p}{i})\times inv_{p\bmod i}invi(p−ip)invpmodi 卡特兰数 组合数公式:HnC2nn−C2nn−1H_nC_{2n}^n-C_{2n}^{n-1}HnC2nn−C2nn−1 递推式:HnHn−1(4n−2)n1H_n\d…...
JavaWeb11-死锁
目录 1.死锁定义 1.1.代码演示 1.2.使用jconsole/jvisualvm/jmc查看死锁 ①使用jconsole:最简单。 ②使用jvisualvm:(Java虚拟机)更方便,更直观,更智能,更高级,是合适的选择。 …...
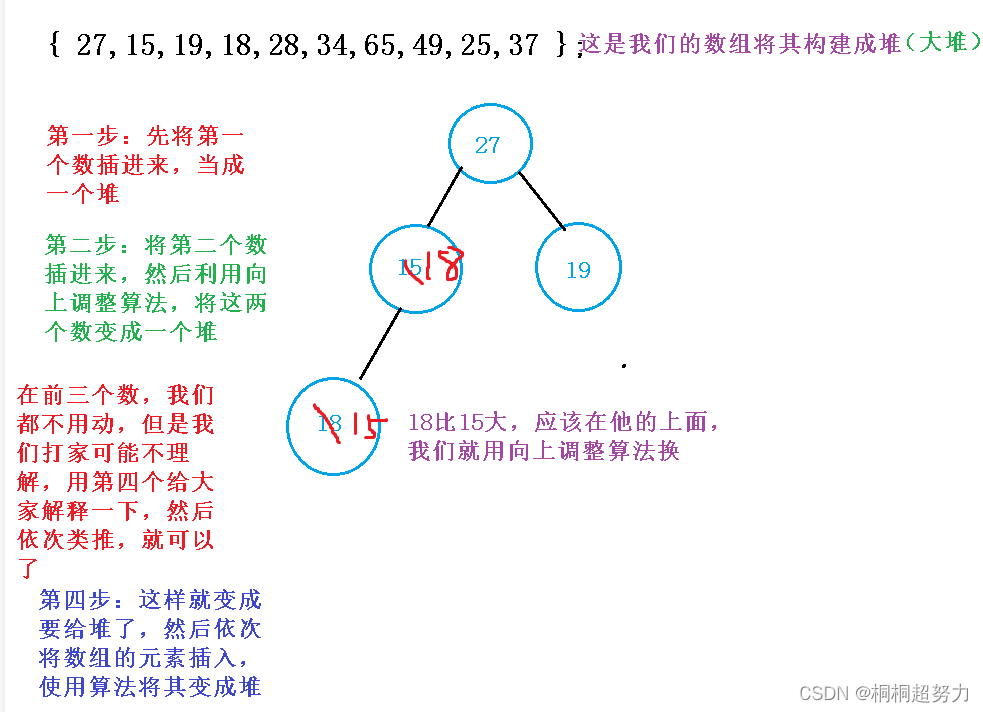
堆的概念和结构以及堆排序
前言 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,…...
【Linux学习笔记】1.Linux 简介及安装
前言 本章介绍Linux及其安装方法。 Linux 简介 Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多…...

代码练习2~
在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。def …...

微信小程序 之 云开发
一、概念1. 传统开发模式2. 新开发模式 ( 云开发模式 )3. 传统、云开发的模式对比4. 传统、云开发的项目流程对比5. 云开发的定位1. 个人的项目或者想法,不想开发服务器,直接使用云开发2. 某些公司的小程序项目是使用云开发的,但是不多&#…...

程序员的三门课,学习成长笔记
最近是有了解到一本好书,叫做程序员的三门课在这本书的内容当中我也确实汲取到了很多前辈能够传达出来的很多关于程序员职业规划以及成长路线上的见解,令我受益匪浅,故此想要把阅读完的每一章节结合自己的工作经验做一个精细化的小结…...

[技术经理]01 程序员最优的成长之路是什么?
00前言 谈起程序员的职业规划,针对大部分的职场人士,最优的成长之路应该是走技术管理路线,而不是走技术专家路线。 01关键的一步 中国自古就有“学而优则仕”的传统,发展到今天,在我们的现代企业里面,尤…...
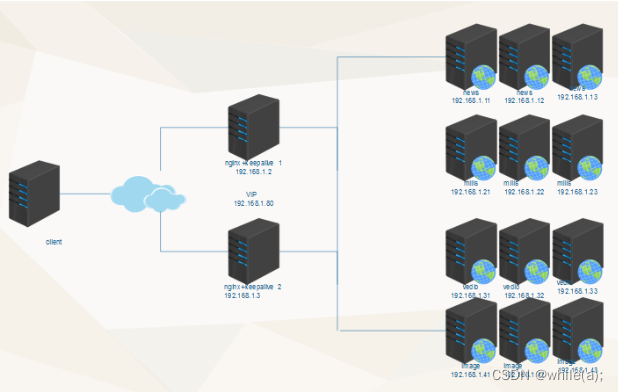
linux集群技术(三)--七层负载均衡-nginx
nginx特点nginx优势、缺点生产架构nginx 7层负载均衡语法示例nginx负载均衡算法测试案例生产案例 1.nginx特点 1. 功能强大,性能卓越,运行稳定。 2. 配置简单灵活。 3. 能够自动剔除工作不正常的后端服务器。 4. 上传文件使用异步模式。client---nginx---web1 web2 web3 lvs同…...
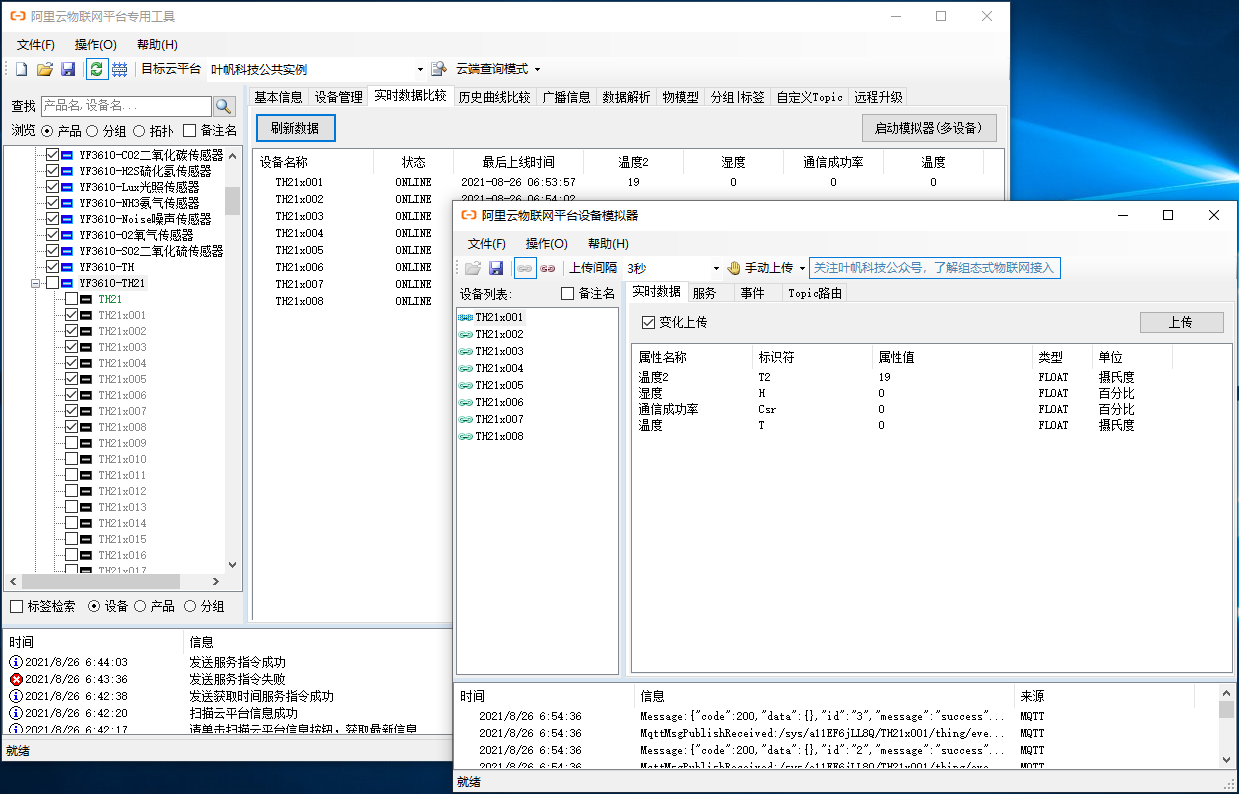
阿里云物联网平台设备模拟器
在使用阿里云物联网平台过程中,如果开始调试没有实际的物理设备,可以考虑在阿里云物联网平台使用官方自带的模拟器进行调试。不过也可以通过叶帆科技开发的阿里云物联网平台设备模拟器AliIoTSimulator进行调试,AliIoTSimulator可以独立运行&a…...
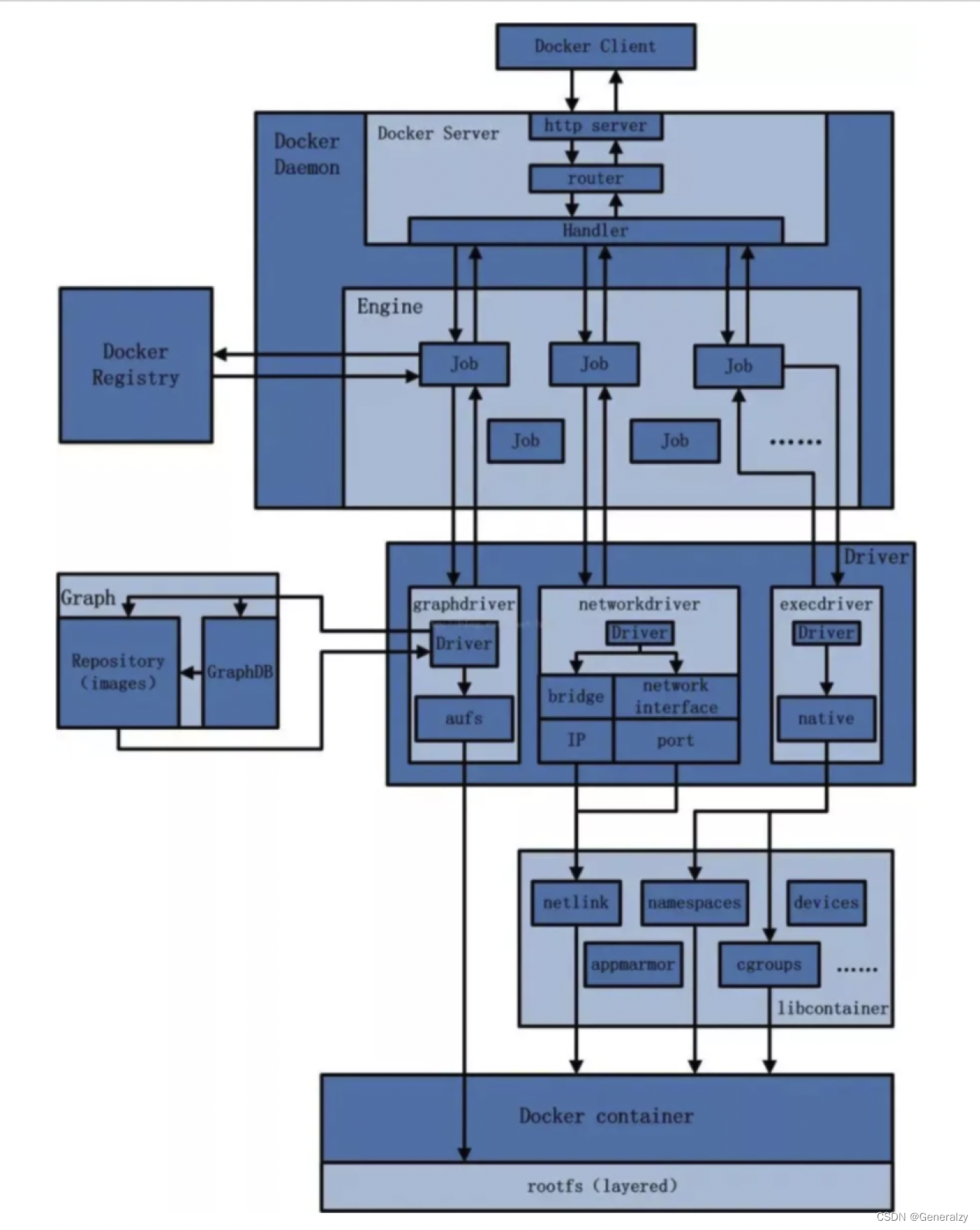
docker全解
目录说明docker简介为什么是docker容器与虚拟机比较容器发展简史传统虚拟机技术容器虚拟化技术docker能干什么带来技术职级的变化开发/运维(Devops)新一代开发工程师Docker应用场景why docker?docker的优势docker和dockerHub官网Docker安装CentOS Docker…...
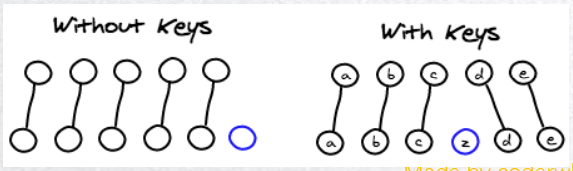
Vue3 基础
Vue3 基础 概述 Vue (发音为 /vjuː/,类似 view) 是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS 和 JavaScript 构建,并提供了一套声明式的、组件化的编程模型,帮助你高效地开发用户界面。无论是简单还是复杂的界面&…...
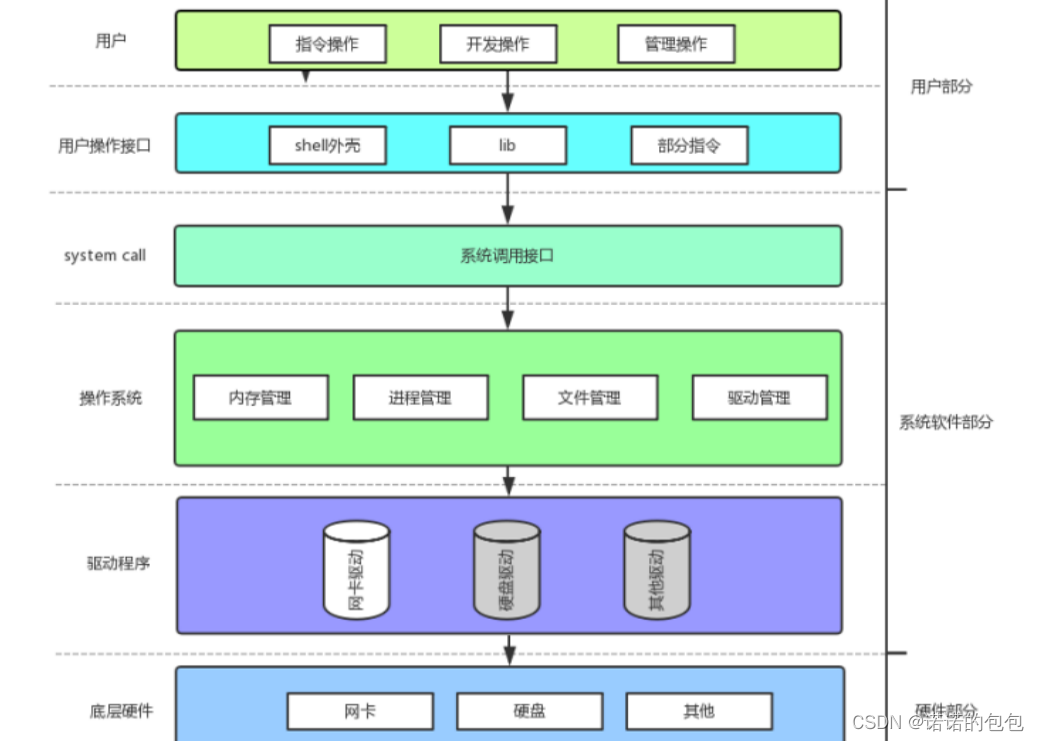
【Linux】冯.诺依曼体系结构与操作系统
环境:centos7.6,腾讯云服务器Linux文章都放在了专栏:【Linux】欢迎支持订阅🌹冯.诺依曼体系结构什么是冯诺依曼体系结构?我们如今的计算机比如笔记本,或者是服务器,基本上都遵循冯诺依曼体系结构…...

WSO2 apim 多租户来区分api
WSO2 apim 多租户来区分api1. Tenant1.1 Add new tenant1.2 Add Role/User1.3 Published Api2. Delete Teant3. AwakeningWSO2安装使用的全过程详解: https://blog.csdn.net/weixin_43916074/article/details/127987099. Official Document: Managing Tenants. 1. Tenant 1.1 …...
)
TodoList(Vue前端经典项目)
TodoList主要是包含了CRUD功能,本地存储功能(loaclStorage)总结:全选按纽可以通过forEach循环来讲数据中的isCheck中的false删除实现就通过传递id,然后根据filter循环将符合条件的数据返回成数组,然后将返回…...

【扫盲】数字货币科普对于完全不了解啥叫比特币的小伙伴需要的聊天谈资
很多人并不清楚,我们时常听说的比特币,以太坊币,等等这些东西到底是一场骗局还是一场货币革命? 下面就围绕这数字货币的历史以及一些应用场景开始分析这个问题。 一、 开端 一切从2008年中本聪(Satoshi Nakamoto&…...

算法学习笔记:双指针
前言: 用于记录总结刷题过程中遇到的同类型问题 双指针问题及用法总结 1. 总结 双指针常用于遍历连序性对象(如数组、链表等)时,使用两个或多个指针进行单向遍历及相应的操作。避免多层循环,降低算法的时间复杂度。 …...

C++类的静态成员总结
tags: C OOP 引子: 类为什么需要静态成员 有时候类需要与它的一些成员与类本身直接相关, 而不是与类的各个对象都保持关联, 这就减少了成员与每一个类的实例对象的联系, 从而降低资源占用. 另一方面, 如果每次都需要重新更新该成员, 使得对象使用新的值, 这时候只需要修改一份…...

二、并发编程的三大特性
文章目录并发编程的三大特性1、原子性什么是并发编程的原子性?保证并发编程的原子性synchronizedCASLock锁ThreadLocal2、可见性什么是可见性?解决可见性的方式volatilesynchronizedLockfinal3、有序性什么是有序性?as-if-serialhappens-beforevolatile并发编程的…...

Ubuntu 22.04.2 LTS安装Apollo8.0
本人硬件环境: CPU:Intel Core i7 6700 显卡(GPU):NVIDIA GTX 3080 10G 内存:SAMSUNG DDR4 32GB 硬盘:双SSD系统盘 2T,双系统(windows,ubuntu) 一、安装Ubuntu 22.04…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

针对药品仓库的效期管理问题,如何利用WMS系统“破局”
案例: 某医药分销企业,主要经营各类药品的批发与零售。由于药品的特殊性,效期管理至关重要,但该企业一直面临效期问题的困扰。在未使用WMS系统之前,其药品入库、存储、出库等环节的效期管理主要依赖人工记录与检查。库…...
