LeetCode_Python_二分查找算法
二分查找
- 算法要求
- 二分查找过程
- 如何更新左右边界
- 实例
- type1:常规记录中间元素
- type2:取跳出循环后的左或右边界
算法要求
- 顺序存储结构
- 元素大小有序
二分查找过程
- 将元素排序;
- 将中间位置记录的这个元素与目标元素比较;
2.1 如果相同,则查找成功;
2.2 否则将元素分为前、后两部分,如果目标元素相比查找元素在左,则更新右边界;如果目标元素相比查找元素在右,则更新左边界;
2.3 重复步骤2
如何更新左右边界
- 查找区间为 [left, right],循环条件为 left <= right;左右分别更新为 mid+1、mid-1
- 查找区间为 [left, right),循环条件为 left < right;左右分别更新为 mid+1、mid
实例
type1:常规记录中间元素
- 有效的平方数
def isPerfectSquare(num):left,right=0,numwhile left<=right:mid=(left+right)//2if mid*mid==num:return Trueelif mid*mid<num:left=mid+1else:right=mid-1return False
type2:取跳出循环后的左或右边界
- 找出X的平方根
注:跳出循环时左右边界的意义,更新前的左右边界分别满足 if 后的条件
def findSqrt(x):left,right=0,xwhile left<=right:mid=(left+right)//2if mid*mid<=x:left=mid+1else:right=mid-1#跳出循环时 left>right,说明上一个更新的是 left,即(left-1)*(left-1)<=x;又 right*right>x,所以left*left>x,因此 left-1 就是要查找的目标数return left-1
- 搜索插入位置
给定一个排序数组nums和一个目标值target,返回目标值索引。如果不存在,返回它将会被按顺序插入的位置。
def searchInsert(nums, target):left,right=0,len(nums)-1while left<=right:mid=(left+right)//2if nums[mid]==target:return midelif nums[mid]<target:left=mid+1else:right=mid-1#跳出循环时后,nums[left-1]<target & nums[right]>target i.e nums[left]>target,因此target要放在left位置return left
相关文章:

LeetCode_Python_二分查找算法
二分查找算法要求二分查找过程如何更新左右边界实例type1:常规记录中间元素type2:取跳出循环后的左或右边界算法要求 顺序存储结构元素大小有序 二分查找过程 将元素排序;将中间位置记录的这个元素与目标元素比较; 2.1 如果相同&a…...
功能测试三年,是时候做出改变了
前言 测试行业3年多经验,学历大专自考本科,主要测试方向web,PC端,wap站,小程序公众号都测试过,app也测过一些,C端B端都有,除功能外,接口性能也有涉猎,但是不…...
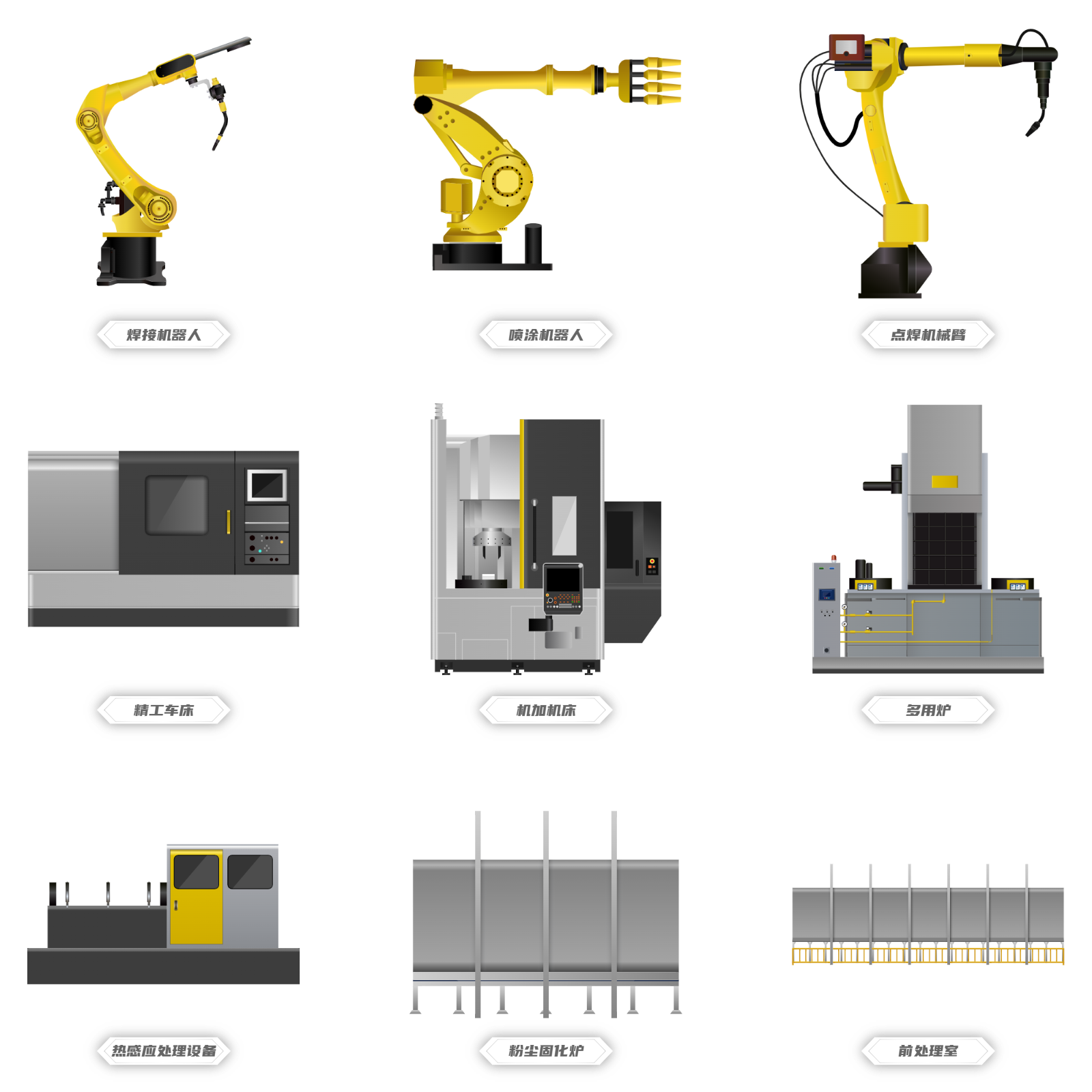
图扑孪生工厂流水线组态图可视化
前言 2018 年,世界经济论坛(WEF)携手麦肯锡公司共同倡议并正式启动了全球“灯塔工厂网络项目”(Lighthouse Network),共同遴选率先应用工业革命 4.0 技术实现企业盈利和持续发展的创新者与示范者。这就使得工厂系统需要对各流水线及生产运行成本方面进行…...
车机开发—【CarService启动流程】
汽车架构:车载HAL是汽车与车辆网络服务之间的接口定义(同时保护传入的数据): 车载HAL与Android Automotive架构: Car App:包括OEM和第三方开发的AppCar API:内有包含CarSensorManager在内的AP…...

webpack中require.context的运用
1. 作用: 利用require创建context (上下文),来告知在编译时具体需要导入哪些模块(即:批量处理待导入模块进行导入); webpack会在构建的时候解析代码中的require.context() (实际上是webpack的方法,vue一般基于webpack…...

2023“Java基础-中级-高级”面试集结,已奉上我的膝盖
Java基础(对象线程字符接口变量异常方法) 面向对象和面向过程的区别? Java 语言有哪些特点? 关于 JVM JDK 和 JRE 最详细通俗的解答 Oracle JDK 和 OpenJDK 的对比 Java 和 C的区别? 什么是 Java 程序的主类&…...

RabbitMQ之发布确认
发布确认 1 发布确认原理 生产者将信道设置成 confirm 模式,一旦信道进入 confirm 模式,所有在该信道上面发布的消息都将会被指派一个唯一的 ID(从 1 开始),一旦消息被投递到所有匹配的队列之后,broker就会发送一个确认给生产者(包含消息的唯一 ID),这就使得生产者知道消…...

一文读懂函数编程及其工作原理
微软MVP实验室研究员 马洪喜-微软 MVP 19年研发经验 云计算咨询顾问专家 容器云及基础架构云技术专家 DevOps 及微服务咨询专家 什么是函数编程 我先用通俗的大白话给大家解释一下函数(Functions, Function as a Service, FaaS)的几个要点,这样看后面示例时才不…...

WSO2 apim Subscribe to an API
WSO2 apim Application Subscribe to an API1. Published an Api2. Subscribe to an API using Key Generation Wizard3. Subscribe to an existing application4. AwakeningWSO2安装使用的全过程详解: https://blog.csdn.net/weixin_43916074/article/details/127987099. Offi…...
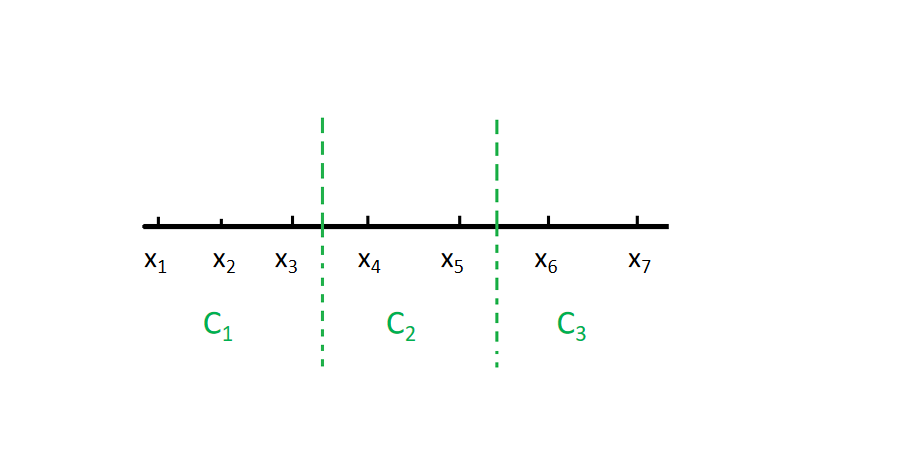
聚类(性能度量)
文章目录聚类(性能度量)外部指标例1内部指标例2聚类(性能度量) 对数据集 D{x1,x2,...,xm}D\{x_1,x_2,...,x_m\}D{x1,x2,...,xm} ,假定通过聚类给出的簇划分为 C{C1,C2,...,Ck}C\{C_1,C_2,...,C_k\}C{C1,C2,…...

GPT-4——比GPT-3强100倍
GPT-4——比GPT-3强100倍 当前世界上最强大的人工智能系统当属ChatGPT。推出2个月用户数就突破1亿。ChatGPT是当下最炙手可热的话题,科技圈几乎人人都在讨论。这边ChatGPT的热度还在不断攀升,另一边来自《纽约时报》的最新报道称ChatGPT即将被自家超越&…...
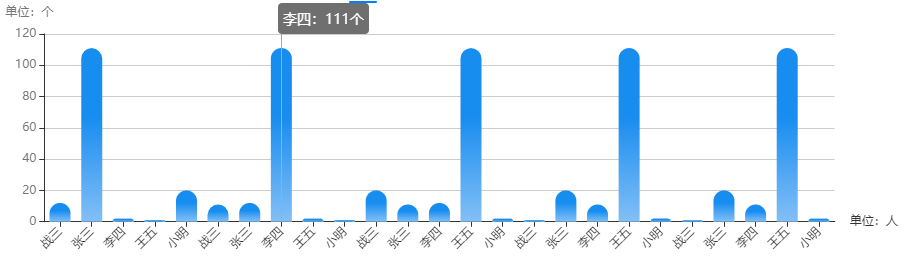
echart中x轴数据过多时展示不全
项目中遇到需要展示一些柱状图,之前做相关功能时,横坐标x轴一直用的是时间,所以没有注意到这个问题。 如下图所示: 当x轴显示的是”人名“这种类型的值的时候,这种显示情况就有问题了,这样就不会知道&…...

关于GIS原理的实际分析应用题的一些解法
话不多说,看题.01 公园选址问题1题目请写出利用GIS技术进行公园选址的空间操作步骤。其中公园选址条件:1)为了安静舒适,要求该园区离主要公路1公里以外,且交通方便,离主要公路3公里以内。2)公园最好依附在大…...

混合精度训练,FP16加速训练,降低内存消耗
计算机中的浮点数表示,按照IEEE754可以分为三种,分别是半精度浮点数、单精度浮点数和双精度浮点数。三种格式的浮点数因占用的存储位数不同,能够表示的数据精度也不同。 Signed bit用于控制浮点数的正负,0表示正数,1表…...

每天五分钟机器学习:新的大规模的机器学习机制——在线学习机制
本文重点 本节课程我们将学习一种新的大规模的机器学习机制--在线学习机制。在线学习机制让我们可以模型化问题。在线学习算法指的是对数据流进行学习而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流,对于每一个用户,网站希望能在不将数据存储到数据库中便顺…...
计算机组成原理错题
静态RAM(SRAM)和动态RAM(DRAM)的基本电路图不同,因此可以通过观察存储器的基本电路图来判断它属于哪一类。 静态RAM的基本电路图包括一个存储单元和一个数据选择器。每个存储单元由一个触发器(flip-flop&a…...

数学基础整理
收纳一些天天忘的结论qwq 线性求逆元 invi(p−pi)invpmodiinv_i(p-\dfrac{p}{i})\times inv_{p\bmod i}invi(p−ip)invpmodi 卡特兰数 组合数公式:HnC2nn−C2nn−1H_nC_{2n}^n-C_{2n}^{n-1}HnC2nn−C2nn−1 递推式:HnHn−1(4n−2)n1H_n\d…...
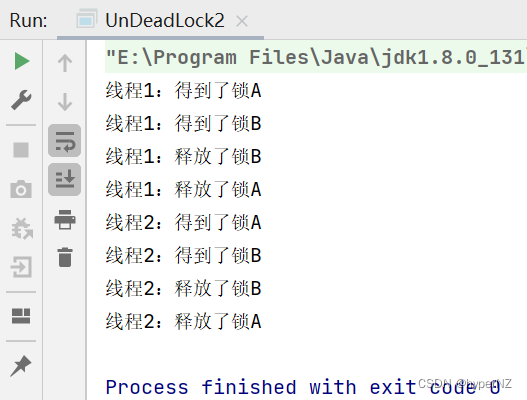
JavaWeb11-死锁
目录 1.死锁定义 1.1.代码演示 1.2.使用jconsole/jvisualvm/jmc查看死锁 ①使用jconsole:最简单。 ②使用jvisualvm:(Java虚拟机)更方便,更直观,更智能,更高级,是合适的选择。 …...
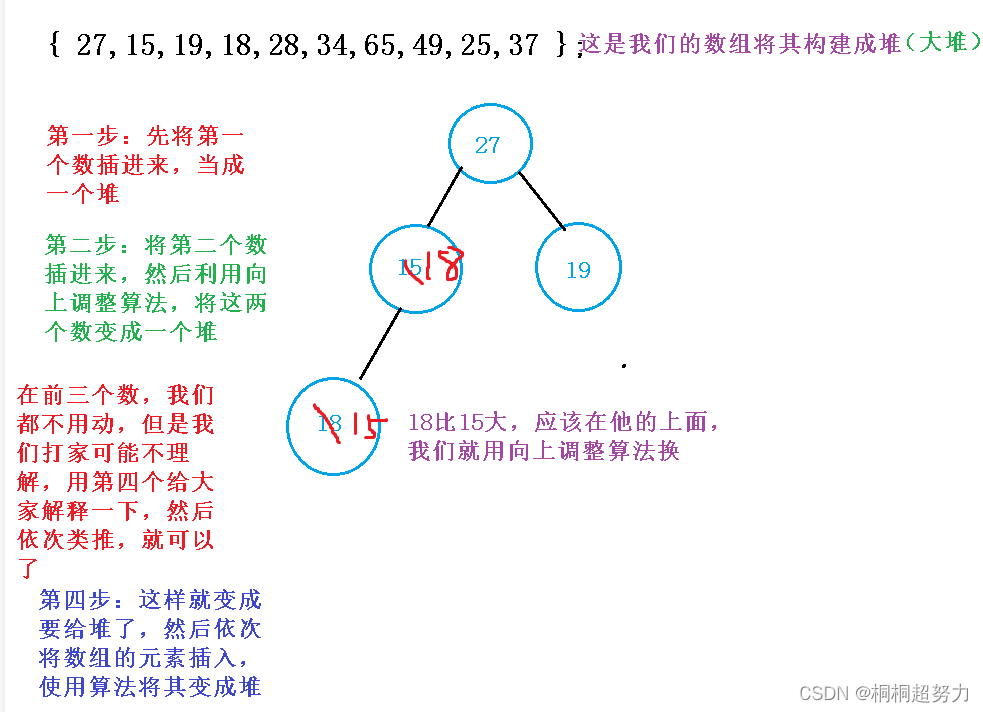
堆的概念和结构以及堆排序
前言 普通的二叉树是不适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结 构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事,…...
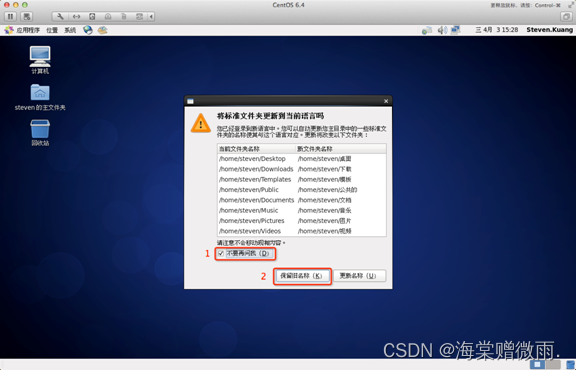
【Linux学习笔记】1.Linux 简介及安装
前言 本章介绍Linux及其安装方法。 Linux 简介 Linux 内核最初只是由芬兰人林纳斯托瓦兹(Linus Torvalds)在赫尔辛基大学上学时出于个人爱好而编写的。 Linux 是一套免费使用和自由传播的类 Unix 操作系统,是一个基于 POSIX 和 UNIX 的多…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
