小白备战大厂算法笔试(八)——搜索
搜索
二分查找
二分查找是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮减少一半搜索范围,直至找到目标元素或搜索区间为空为止。
Question:
给定一个长度为n的数组
nums,元素按从小到大的顺序排列,数组不包含重复元素。请查找并返回元素target在该数组中的索引。若数组不包含该元素,则返回 −1
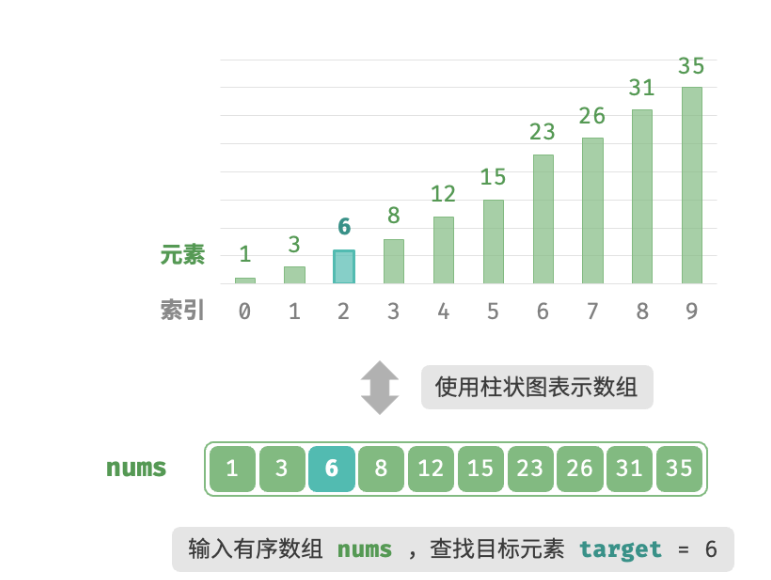
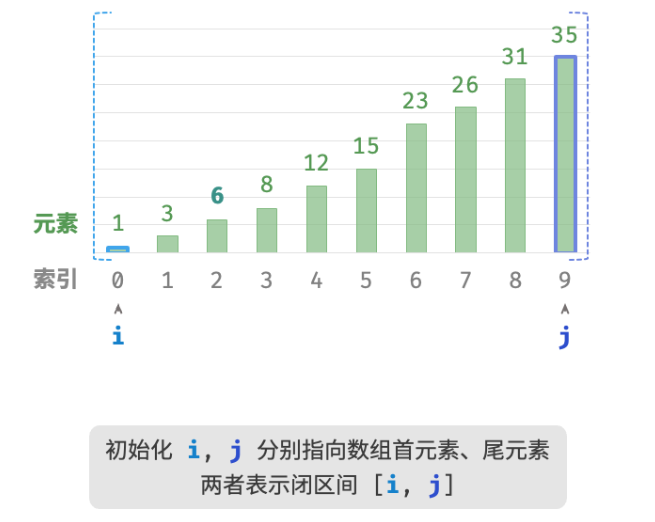
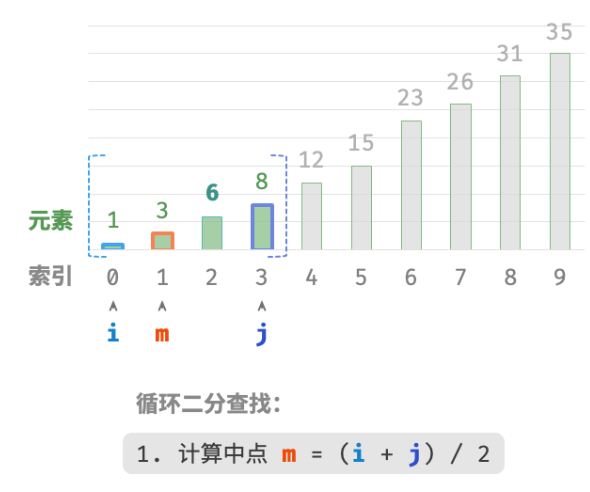
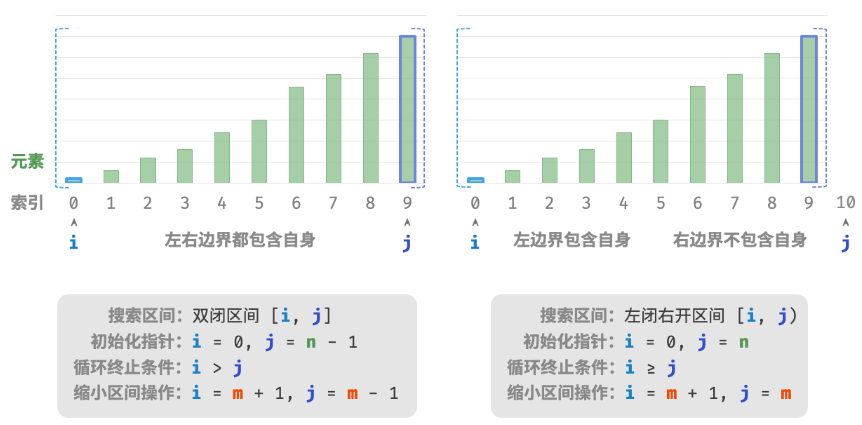
双闭区间
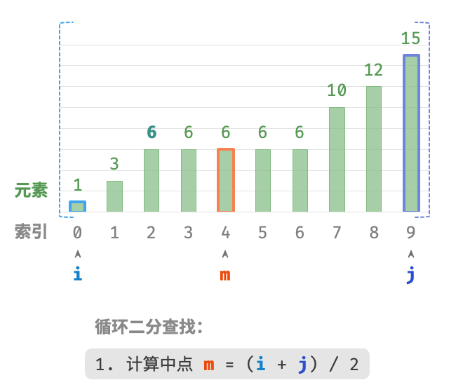
如下图所示,我们先初始化指针i=0 和 j=n−1 ,分别指向数组首元素和尾元素,代表搜索区间 [0,n−1] 。请注意,中括号表示闭区间,其包含边界值本身。
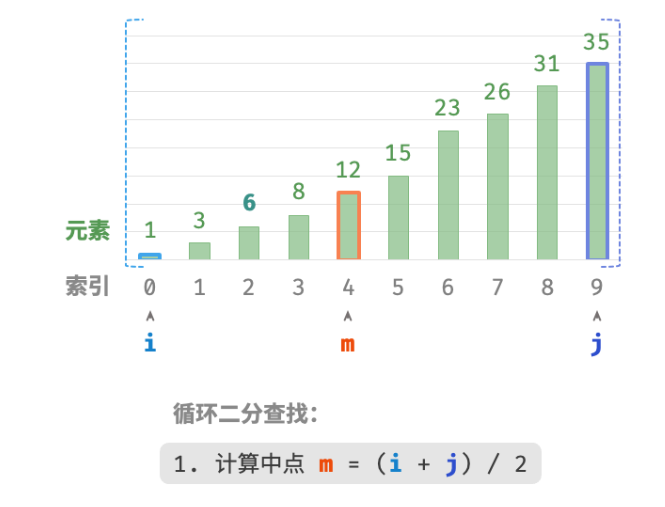
接下来,循环执行以下两步。
-
计算中点索引 m=⌊(i+j)/2⌋ ,其中 ⌊⌋ 表示向下取整操作。
-
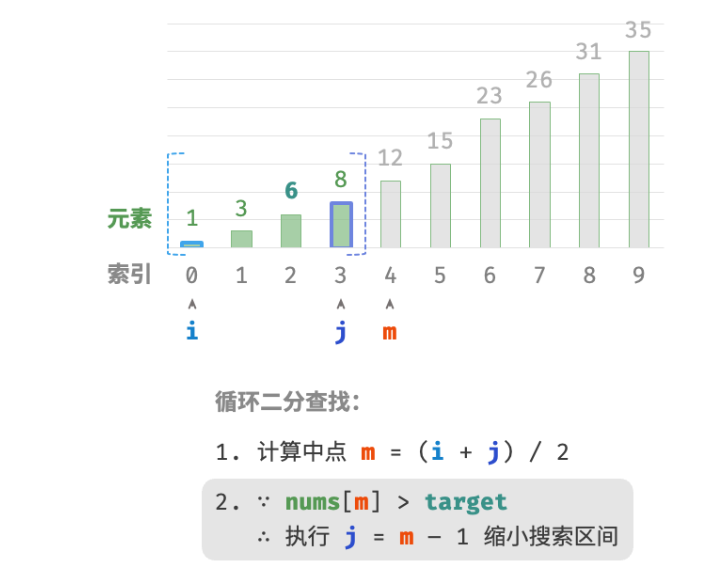
判断
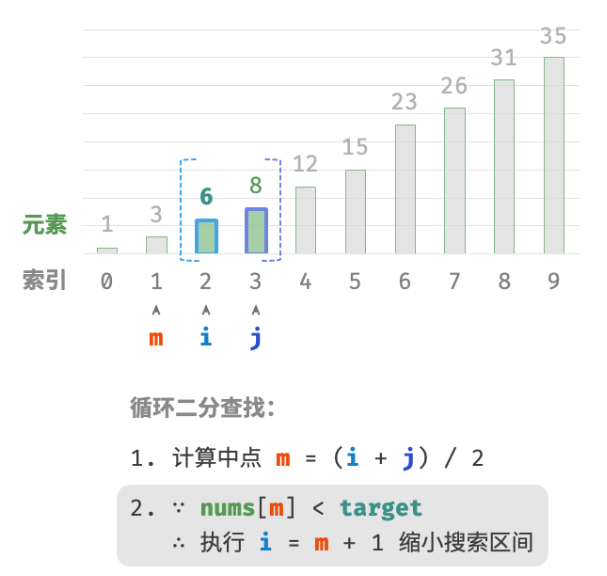
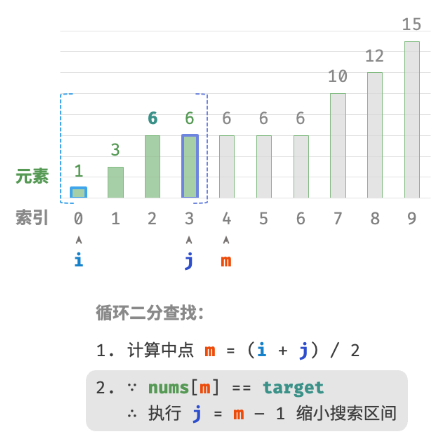
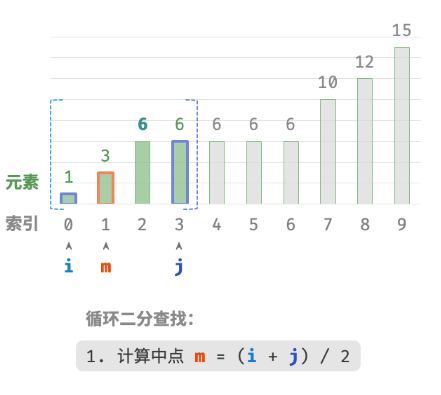
nums[m]和target的大小关系,分为以下三种情况。-
当
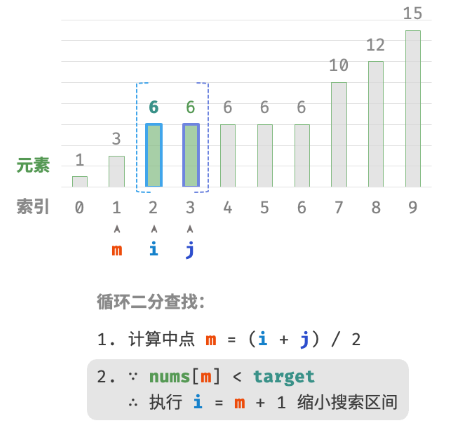
nums[m] < target时,说明target在区间 [m+1,j] 中,因此执行 i=m+1 。 -
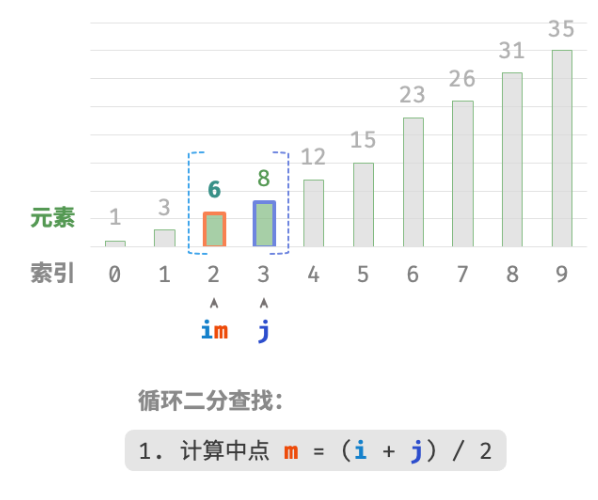
当
nums[m] > target时,说明target在区间 [i,m−1] 中,因此执行 j=m−1 。 -
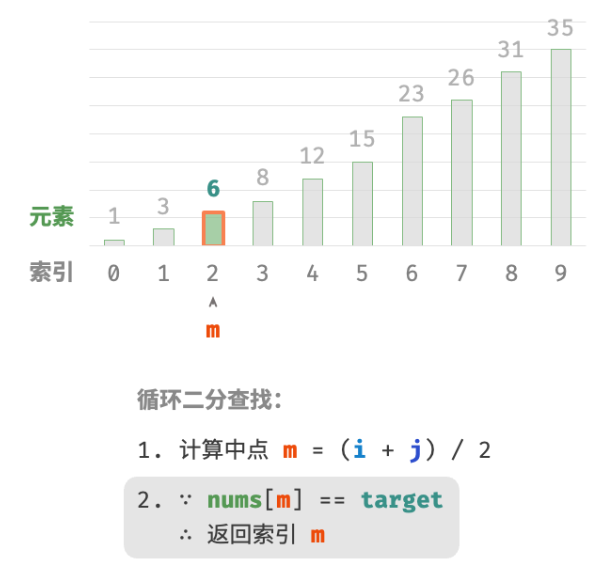
当
nums[m] = target时,说明找到target,因此返回索引 m 。
-
若数组不包含目标元素,搜索区间最终会缩小为空。此时返回 −1 。
值得注意的是,由于 i 和 j 都是 int 类型,因此 i+j 可能会超出 int 类型的取值范围。为了避免大数越界,我们通常采用公式 m=⌊i+(j−i)/2⌋ 来计算中点。
Python:
def binary_search(nums: list[int], target: int) -> int:"""二分查找(双闭区间)"""# 初始化双闭区间 [0, n-1] ,即 i, j 分别指向数组首元素、尾元素i, j = 0, len(nums) - 1# 循环,当搜索区间为空时跳出(当 i > j 时为空)while i <= j:# 理论上 Python 的数字可以无限大(取决于内存大小),无须考虑大数越界问题m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # 此情况说明 target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1 # 此情况说明 target 在区间 [i, m-1] 中else:return m # 找到目标元素,返回其索引return -1 # 未找到目标元素,返回 -1
Go:
/* 二分查找(双闭区间) */
func binarySearch(nums []int, target int) int {// 初始化双闭区间 [0, n-1] ,即 i, j 分别指向数组首元素、尾元素i, j := 0, len(nums)-1// 循环,当搜索区间为空时跳出(当 i > j 时为空)for i <= j {m := i + (j-i)/2 // 计算中点索引 mif nums[m] < target { // 此情况说明 target 在区间 [m+1, j] 中i = m + 1} else if nums[m] > target { // 此情况说明 target 在区间 [i, m-1] 中j = m - 1} else { // 找到目标元素,返回其索引return m}}// 未找到目标元素,返回 -1return -1
}
时间复杂度 O(logn) :在二分循环中,区间每轮缩小一半,循环次数为 log₂n 。
空间复杂度 O(1) :指针 i 和 j 使用常数大小空间。
左开右闭
除了上述的双闭区间外,常见的区间表示还有“左闭右开”区间,定义为 [0,n) ,即左边界包含自身,右边界不包含自身。在该表示下,区间 [i,j] 在 i=j 时为空。可以基于该表示实现具有相同功能的二分查找算法。
Python:
def binary_search_lcro(nums: list[int], target: int) -> int:"""二分查找(左闭右开)"""# 初始化左闭右开 [0, n) ,即 i, j 分别指向数组首元素、尾元素+1i, j = 0, len(nums)# 循环,当搜索区间为空时跳出(当 i = j 时为空)while i < j:m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # 此情况说明 target 在区间 [m+1, j) 中elif nums[m] > target:j = m # 此情况说明 target 在区间 [i, m) 中else:return m # 找到目标元素,返回其索引return -1 # 未找到目标元素,返回 -1
Go:
/* 二分查找(左闭右开) */
func binarySearchLCRO(nums []int, target int) int {// 初始化左闭右开 [0, n) ,即 i, j 分别指向数组首元素、尾元素+1i, j := 0, len(nums)// 循环,当搜索区间为空时跳出(当 i = j 时为空)for i < j {m := i + (j-i)/2 // 计算中点索引 mif nums[m] < target { // 此情况说明 target 在区间 [m+1, j) 中i = m + 1} else if nums[m] > target { // 此情况说明 target 在区间 [i, m) 中j = m} else { // 找到目标元素,返回其索引return m}}// 未找到目标元素,返回 -1return -1
}
在两种区间表示下,二分查找算法的初始化、循环条件和缩小区间操作皆有所不同。由于“双闭区间”表示中的左右边界都被定义为闭区间,因此指针 i 和 j 缩小区间操作也是对称的。这样更不容易出错,因此一般建议采用“双闭区间”的写法。
优缺点
二分查找在时间和空间方面都有较好的性能。
- 二分查找的时间效率高。在大数据量下,对数阶的时间复杂度具有显著优势。
- 二分查找无须额外空间。相较于需要借助额外空间的搜索算法(例如哈希查找),二分查找更加节省空间。
然而,二分查找并非适用于所有情况,主要有以下原因。
- 二分查找仅适用于有序数据。若输入数据无序,为了使用二分查找而专门进行排序,得不偿失。因为排序算法的时间复杂度通常为 O(nlogn) ,比线性查找和二分查找都更高。对于频繁插入元素的场景,为保持数组有序性,需要将元素插入到特定位置,时间复杂度为 O(n) ,也是非常昂贵的。
- 二分查找仅适用于数组。二分查找需要跳跃式(非连续地)访问元素,而在链表中执行跳跃式访问的效率较低,因此不适合应用在链表或基于链表实现的数据结构。
- 小数据量下,线性查找性能更佳。在线性查找中,每轮只需要 1 次判断操作;而在二分查找中,需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法(减法),共 4 ~ 6 个单元操作;因此,当数据量 n 较小时,线性查找反而比二分查找更快。
二分查找插入点
二分查找不仅可用于搜索目标元素,还具有许多变种问题,比如搜索目标元素的插入位置。
无重复元素
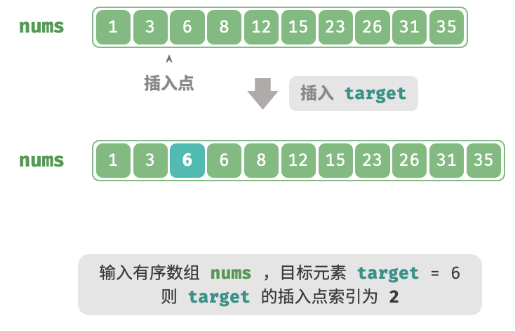
Question
给定一个长度为 n 的有序数组
nums和一个元素target,数组不存在重复元素。现将target插入到数组nums中,并保持其有序性。若数组中已存在元素target,则插入到其左方。请返回插入后target在数组中的索引。
Python:
def binary_search_insertion_simple(nums: list[int], target: int) -> int:"""二分查找插入点(无重复元素)"""i, j = 0, len(nums) - 1 # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1 # target 在区间 [i, m-1] 中else:return m # 找到 target ,返回插入点 m# 未找到 target ,返回插入点 ireturn i
Go:
/* 二分查找插入点(无重复元素) */
func binarySearchInsertionSimple(nums []int, target int) int {// 初始化双闭区间 [0, n-1]i, j := 0, len(nums)-1for i <= j {// 计算中点索引 mm := i + (j-i)/2if nums[m] < target {// target 在区间 [m+1, j] 中i = m + 1} else if nums[m] > target {// target 在区间 [i, m-1] 中j = m - 1} else {// 找到 target ,返回插入点 mreturn m}}// 未找到 target ,返回插入点 ireturn i
}
有重复元素
假设数组中存在多个 target ,则普通二分查找只能返回其中一个 target 的索引,而无法确定该元素的左边和右边还有多少 target。
题目要求将目标元素插入到最左边,所以我们需要查找数组中最左一个 target 的索引。
- 执行二分查找,得到任意一个
target的索引,记为 k 。 - 从索引 k 开始,向左进行线性遍历,当找到最左边的
target时返回。
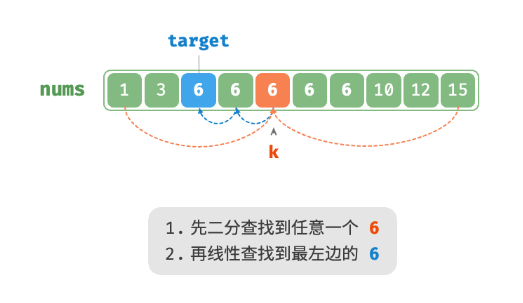
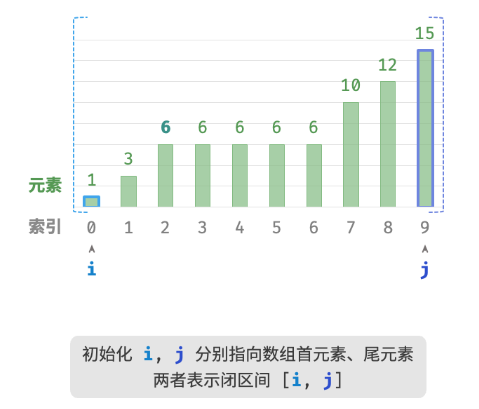
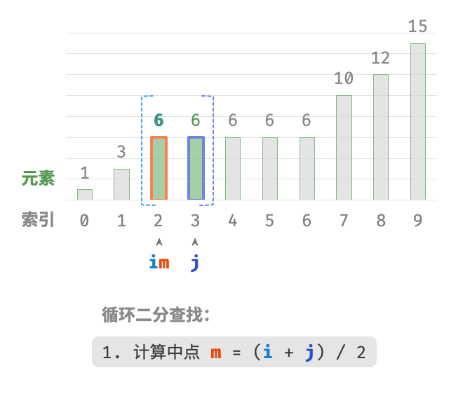
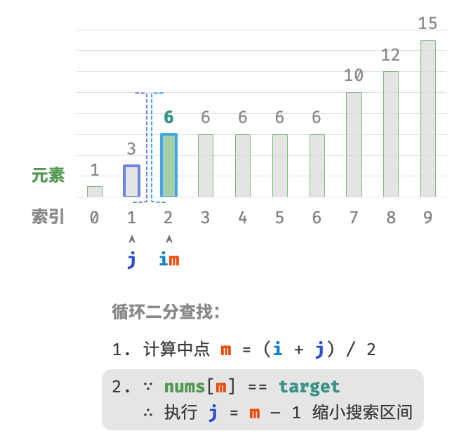
此方法虽然可用,但其包含线性查找,因此时间复杂度为 O(n) 。当数组中存在很多重复的 target 时,该方法效率很低。现考虑拓展二分查找代码。整体流程保持不变,每轮先计算中点索引 m ,再判断 target 和 nums[m] 大小关系,分为以下几种情况。
- 当
nums[m] < target或nums[m] > target时,说明还没有找到target,因此采用普通二分查找的缩小区间操作,从而使指针 i 和 i 向target靠近。 - 当
nums[m] == target时,说明小于target的元素在区间 [i,m−1] 中,因此采用 j=m−1 来缩小区间,从而使指针 j 向小于target的元素靠近。
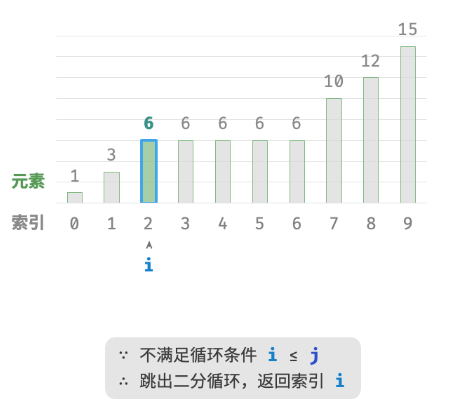
循环完成后,i 指向最左边的 target ,j 指向首个小于 target 的元素,因此索引 i 就是插入点。
Python:
def binary_search_insertion(nums: list[int], target: int) -> int:"""二分查找插入点(存在重复元素)"""i, j = 0, len(nums) - 1 # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2 # 计算中点索引 mif nums[m] < target:i = m + 1 # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1 # target 在区间 [i, m-1] 中else:j = m - 1 # 首个小于 target 的元素在区间 [i, m-1] 中# 返回插入点 ireturn i
Go:
/* 二分查找插入点(存在重复元素) */
func binarySearchInsertion(nums []int, target int) int {// 初始化双闭区间 [0, n-1]i, j := 0, len(nums)-1for i <= j {// 计算中点索引 mm := i + (j-i)/2if nums[m] < target {// target 在区间 [m+1, j] 中i = m + 1} else if nums[m] > target {// target 在区间 [i, m-1] 中j = m - 1} else {// 首个小于 target 的元素在区间 [i, m-1] 中j = m - 1}}// 返回插入点 ireturn i
}
二分查找边界
左边界
Question
给定一个长度为 n 的有序数组
nums,数组可能包含重复元素。请返回数组中最左一个元素target的索引。若数组中不包含该元素,则返回 −1 。
回忆二分查找插入点的方法,搜索完成后 i 指向最左一个 target ,因此查找插入点本质上是在查找最左一个 target 的索引。考虑通过查找插入点的函数实现查找左边界。请注意,数组中可能不包含 target ,这种情况可能导致以下两种结果。
- 插入点的索引 i 越界。
- 元素
nums[i]与target不相等。
当遇到以上两种情况时,直接返回 −1 即可。
为什么
i可能会越界?
考虑一个例子:
假设我们有一个数组 nums = [1, 2, 3, 4, 5] 并且我们的目标值 target = 6。使用上述的二分查找插入点方法,我们将会得到以下的过程:
- i=0, j=4, m=2, nums[m]=3, 3 < 6, 所以 i=m+1=3。
- i=3, j=4, m=3, nums[m]=4, 4 < 6, 所以 i=m+1=4。
- i=4, j=4, m=4, nums[m]=5, 5 < 6, 所以 i=m+1=5。
现在 i 指向了索引 5,这是越界的,因为数组的最大索引是 4。
Python:
def binary_search_left_edge(nums: list[int], target: int) -> int:"""二分查找最左一个 target"""# 等价于查找 target 的插入点i = binary_search_insertion(nums, target)# 未找到 target ,返回 -1if i == len(nums) or nums[i] != target:return -1# 找到 target ,返回索引 ireturn i
Go:
/* 二分查找最左一个 target */
func binarySearchLeftEdge(nums []int, target int) int {// 等价于查找 target 的插入点i := binarySearchInsertion(nums, target)// 未找到 target ,返回 -1if i == len(nums) || nums[i] != target {return -1}// 找到 target ,返回索引 ireturn i
}
右边界
复用查找左边界
可以利用查找最左元素的函数来查找最右元素,具体方法为:将查找最右一个 target 转化为查找最左一个 target + 1。如下图所示,查找完成后,指针 i 指向最左一个 target + 1(如果存在),而 j 指向最右一个 target ,因此返回 j 即可。
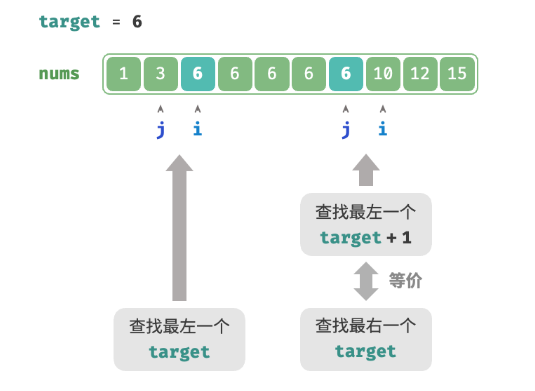
请注意,返回的插入点是 i ,因此需要将其减 1 ,从而获得 j 。
Python:
def binary_search_right_edge(nums: list[int], target: int) -> int:"""二分查找最右一个 target"""# 转化为查找最左一个 target + 1i = binary_search_insertion(nums, target + 1)# j 指向最右一个 target ,i 指向首个大于 target 的元素j = i - 1# 未找到 target ,返回 -1if j == -1 or nums[j] != target:return -1# 找到 target ,返回索引 jreturn j
Go:
/* 二分查找最右一个 target */
func binarySearchRightEdge(nums []int, target int) int {// 转化为查找最左一个 target + 1i := binarySearchInsertion(nums, target+1)// j 指向最右一个 target ,i 指向首个大于 target 的元素j := i - 1// 未找到 target ,返回 -1if j == -1 || nums[j] != target {return -1}// 找到 target ,返回索引 jreturn j
}
查找不存在元素
当数组不包含 target 时,最终 i 和 j 会分别指向首个大于、小于 target 的元素。可以构造一个数组中不存在的元素,用于查找左右边界。
- 查找最左一个
target:可以转化为查找target - 0.5,并返回指针 i 。 - 查找最右一个
target:可以转化为查找target + 0.5,并返回指针 j 。
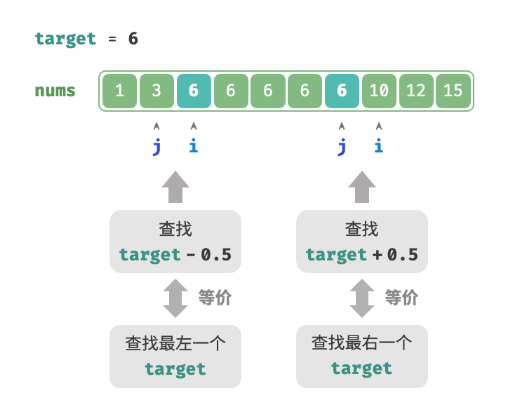
- 给定数组不包含小数,这意味着我们无须关心如何处理相等的情况。
- 因为该方法引入了小数,所以需要将函数中的变量
target改为浮点数类型。
哈希优化
在算法题中,常通过将线性查找替换为哈希查找来降低算法的时间复杂度。
Question
给定一个整数数组
nums和一个目标元素target,请在数组中搜索“和”为target的两个元素,并返回它们的数组索引。返回任意一个解即可。
线性查找
直接遍历所有可能的组合。开启一个两层循环,在每轮中判断两个整数的和是否为 target ,若是则返回它们的索引。

Python:
def two_sum_brute_force(nums: list[int], target: int) -> list[int]:"""方法一:暴力枚举"""# 两层循环,时间复杂度 O(n^2)for i in range(len(nums) - 1):for j in range(i + 1, len(nums)):if nums[i] + nums[j] == target:return [i, j]return []
Go:
/* 方法一:暴力枚举 */
func twoSumBruteForce(nums []int, target int) []int {size := len(nums)// 两层循环,时间复杂度 O(n^2)for i := 0; i < size-1; i++ {for j := i + 1; i < size; j++ {if nums[i]+nums[j] == target {return []int{i, j}}}}return nil
}
此方法的时间复杂度为 O(n^2) ,空间复杂度为 O(1) ,在大数据量下非常耗时。
哈希查找
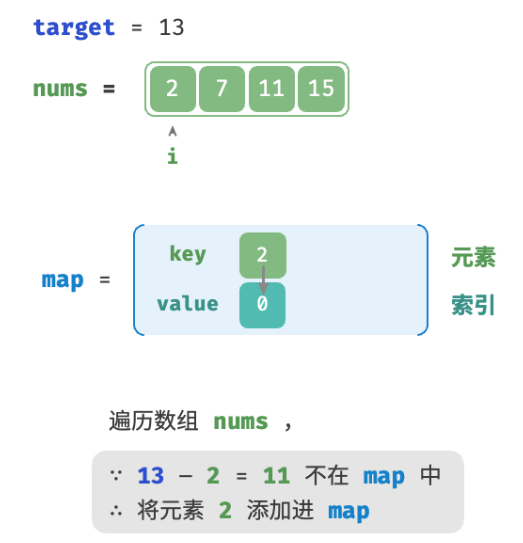
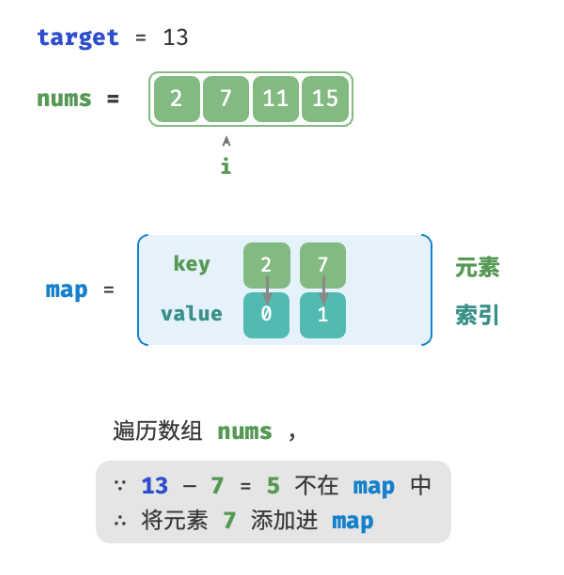
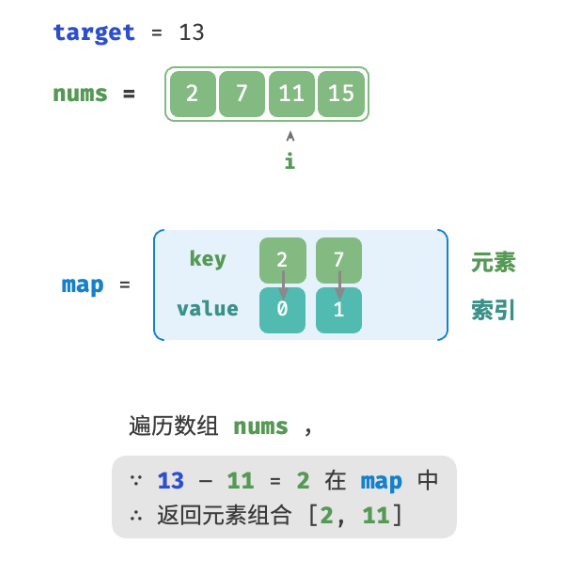
考虑借助一个哈希表,键值对分别为数组元素和元素索引。循环遍历数组:
- 判断数字
target - nums[i]是否在哈希表中,若是则直接返回这两个元素的索引。 - 将键值对
nums[i]和索引i添加进哈希表。
Python:
def two_sum_hash_table(nums: list[int], target: int) -> list[int]:"""方法二:辅助哈希表"""# 辅助哈希表,空间复杂度 O(n)dic = {}# 单层循环,时间复杂度 O(n)for i in range(len(nums)):if target - nums[i] in dic:return [dic[target - nums[i]], i]dic[nums[i]] = ireturn []
Go:
/* 方法二:辅助哈希表 */
func twoSumHashTable(nums []int, target int) []int {// 辅助哈希表,空间复杂度 O(n)hashTable := map[int]int{}// 单层循环,时间复杂度 O(n)for idx, val := range nums {if preIdx, ok := hashTable[target-val]; ok {return []int{preIdx, idx}}hashTable[val] = idx}return nil
}
此方法通过哈希查找将时间复杂度从 O(n^2) 降低至 O(n) ,大幅提升运行效率。由于需要维护一个额外的哈希表,因此空间复杂度为 O(n) 。尽管如此,该方法的整体时空效率更为均衡,因此它是本题的最优解法。
搜索算法
搜索算法用于在数据结构(例如数组、链表、树或图)中搜索一个或一组满足特定条件的元素。
搜索算法可根据实现思路分为以下两类。
- 通过遍历数据结构来定位目标元素,例如数组、链表、树和图的遍历等。
- 利用数据组织结构或数据包含的先验信息,实现高效元素查找,例如二分查找、哈希查找和二叉搜索树查找等。
暴力搜索
暴力搜索通过遍历数据结构的每个元素来定位目标元素。
- “线性搜索”适用于数组和链表等线性数据结构。它从数据结构的一端开始,逐个访问元素,直到找到目标元素或到达另一端仍没有找到目标元素为止。
- “广度优先搜索”和“深度优先搜索”是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索,由近及远地访问各个节点。深度优先搜索是从初始节点开始,沿着一条路径走到头为止,再回溯并尝试其他路径,直到遍历完整个数据结构。
暴力搜索的优点是简单且通用性好,无须对数据做预处理和借助额外的数据结构。
然而,此类算法的时间复杂度为 O(n) ,其中 n 为元素数量,因此在数据量较大的情况下性能较差。
自适应搜索
自适应搜索利用数据的特有属性(例如有序性)来优化搜索过程,从而更高效地定位目标元素。
- “二分查找”利用数据的有序性实现高效查找,仅适用于数组。
- “哈希查找”利用哈希表将搜索数据和目标数据建立为键值对映射,从而实现查询操作。
- “树查找”在特定的树结构(例如二叉搜索树)中,基于比较节点值来快速排除节点,从而定位目标元素。
此类算法的优点是效率高,时间复杂度可达到 O(logn) 甚至 O(1) 。
然而,使用这些算法往往需要对数据进行预处理。例如,二分查找需要预先对数组进行排序,哈希查找和树查找都需要借助额外的数据结构,维护这些数据结构也需要额外的时间和空间开支。
搜索算法选取
给定大小为 n 的一组数据,我们可以使用线性搜索、二分查找、树查找、哈希查找等多种方法在该数据中搜索目标元素。
| 线性搜索 | 二分查找 | 树查找 | 哈希查找 | |
|---|---|---|---|---|
| 查找元素 | O(n) | O(logn) | O(logn) | O(1) |
| 插入元素 | O(1) | O(n) | O(logn) | O(1) |
| 删除元素 | O(n) | O(n) | O(logn) | O(1) |
| 额外空间 | O(1) | O(1) | O(n) | O(n) |
| 数据预处理 | / | 排序 O(nlogn) | 建树 O(nlogn) | 建哈希表 O(n) |
| 数据是否有序 | 无序 | 有序 | 有序 | 无序 |
搜索算法的选择还取决于数据体量、搜索性能要求、数据查询与更新频率等。
线性搜索
- 通用性较好,无须任何数据预处理操作。假如我们仅需查询一次数据,那么其他三种方法的数据预处理的时间比线性搜索的时间还要更长。
- 适用于体量较小的数据,此情况下时间复杂度对效率影响较小。
- 适用于数据更新频率较高的场景,因为该方法不需要对数据进行任何额外维护。
二分查找
- 适用于大数据量的情况,效率表现稳定,最差时间复杂度为 O(logn) 。
- 数据量不能过大,因为存储数组需要连续的内存空间。
- 不适用于高频增删数据的场景,因为维护有序数组的开销较大。
哈希查找
- 适合对查询性能要求很高的场景,平均时间复杂度为 O(1) 。
- 不适合需要有序数据或范围查找的场景,因为哈希表无法维护数据的有序性。
- 对哈希函数和哈希冲突处理策略的依赖性较高,具有较大的性能劣化风险。
- 不适合数据量过大的情况,因为哈希表需要额外空间来最大程度地减少冲突,从而提供良好的查询性能。
树查找
- 适用于海量数据,因为树节点在内存中是离散存储的。
- 适合需要维护有序数据或范围查找的场景。
- 在持续增删节点的过程中,二叉搜索树可能产生倾斜,时间复杂度劣化至 O(n) 。
- 若使用 AVL 树或红黑树,则各项操作可在 O(logn) 效率下稳定运行,但维护树平衡的操作会增加额外开销。
References:https://www.hello-algo.com/chapter_searching/
相关文章:

小白备战大厂算法笔试(八)——搜索
搜索 二分查找 二分查找是一种基于分治策略的高效搜索算法。它利用数据的有序性,每轮减少一半搜索范围,直至找到目标元素或搜索区间为空为止。 Question: 给定一个长度为n的数组 nums ,元素按从小到大的顺序排列,数组…...

〔022〕Stable Diffusion 之 生成视频 篇
✨ 目录 🎈 视频转换 / mov2mov🎈 视频转换前奏准备🎈 视频转换 mov2mov 使用🎈 视频转换 mov2mov 效果预览🎈 视频无限缩放 / Infinite Zoom🎈 视频无限缩放 Infinite Zoom 使用 🎈 视频转换 /…...
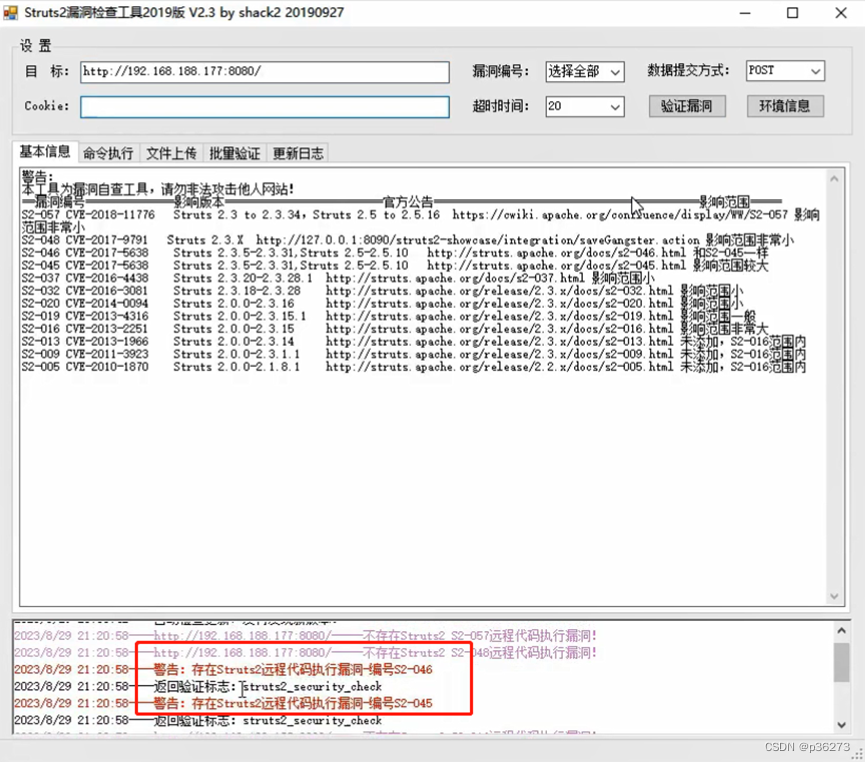
网络安全深入学习第三课——热门框架漏洞(RCE—Struts2远程代码执行)
文章目录 一、Struts2框架介绍二、Struts2远程代码执行漏洞三、Struts2执行代码的原理四、Struts2框架特征五、漏洞手工POC六、漏洞工具复现 一、Struts2框架介绍 ------ Struts2是apache项目下的一个web 框架,普遍应用于阿里巴巴、京东等互联网、政府、企业门户网…...

【uni-app】
准备工作(Hbuilder) 1.下载hbuilder,插件使用Vue3的uni-app项目 2.需要安装编译器 3.下载微信开发者工具 4.点击运行->微信开发者工具 5.打开微信开发者工具的服务端口 效果图 准备工作(VScode) 插件 uni-cr…...
Pytorch 多卡并行(3)—— 使用 DDP 加速 minGPT 训练
前文 并行原理简介和 DDP 并行实践 和 使用 torchrun 进行容错处理 在简单的随机数据上演示了使用 DDP 并行加速训练的方法,本文考虑一个更加复杂的 GPT 类模型,说明如何进行 DDP 并行实战MinGPT 是 GPT 模型的一个流行的开源 PyTorch 复现项目ÿ…...
IAM、EIAM、CIAM、RAM、IDaaS 都是什么?
后端程序员在做 ToB 产品或者后台系统时,都不可避免的会遇到账号系统、登录系统、权限系统、日志系统等这些核心功能。这些功能一般都是以 SSO 系统、RBAC 权限管理系统等方式命名,但这些系统合起来有一个专有名词:IAM。 IAM IAM 是 Identi…...
STM32 Cubemx 通用定时器 General-Purpose Timers同步
文章目录 前言简介cubemx配置 前言 持续学习stm32中… 简介 通用定时器是一个16位的计数器,支持向上up、向下down与中心对称up-down三种模式。可以用于测量信号脉宽(输入捕捉),输出一定的波形(比较输出与PWM输出&am…...

Ubuntu 20.04降级clang-format
1. 卸载clang-format sudo apt purge clang-format 2. 安装clang-format-6.0 sudo apt install clang-format-6.0 3. 软链接clang-format sudo ln -s /usr/bin/clang-format-6.0 /usr/bin/clang-format...

激活函数总结(三十四):激活函数补充(FReLU、CReLU)
激活函数总结(三十四):激活函数补充 1 引言2 激活函数2.1 FReLU激活函数2.2 CReLU激活函数 3. 总结 1 引言 在前面的文章中已经介绍了介绍了一系列激活函数 (Sigmoid、Tanh、ReLU、Leaky ReLU、PReLU、Swish、ELU、SELU、GELU、Softmax、Sof…...

【LeetCode-简单题KMP】459. 重复的子字符串
文章目录 题目方法一:移动匹配方法二:KMP算法 题目 方法一:移动匹配 class Solution {//移动匹配public boolean repeatedSubstringPattern(String s) {StringBuffer str new StringBuffer(s);//ababstr.append(s);//拼接一份自己 abababab…...

Lua脚本
基本语法 注释 print(“script lua win”) – 单行注释 – [[ 多行注释 ]] – 标识符 类似于:java当中 变量、属性名、方法名。 以字母(a-z,A-Z)、下划线 开头,后面加上0个或多个 字母、下划线、数字。 不要用下划线大写字母…...

vue 封装一个Dialog组件
基于element-plus封装一个Dialog组件 <template><section class"dialog-wrap"><el-dialog :title"title" v-model"visible" :close-on-click-modal"false"><section class"content-wrap"><Form…...
外包干了2个月,技术退步明显。。。。。
先说一下自己的情况,大专生,18年通过校招进入武汉某软件公司,干了接近4年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
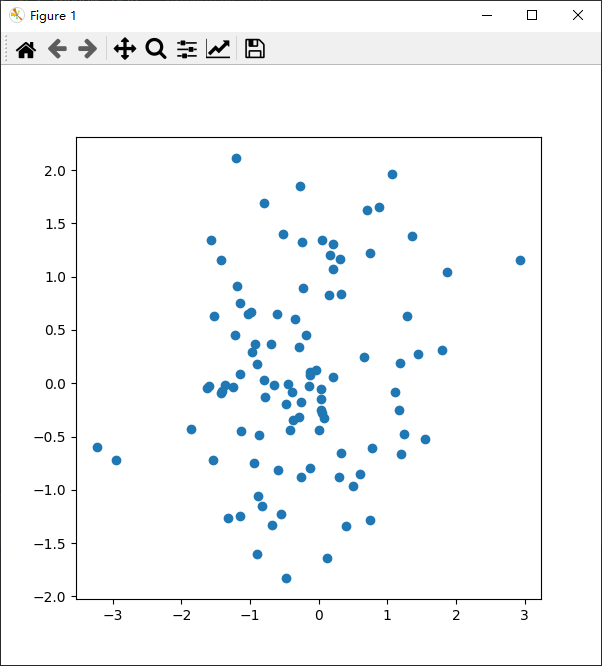
python科研作图
1、气泡图 气泡图是一种在xy轴上显示三个维度的数据的有效方式。在气泡图中,基本上,每个气泡代表一个数据点。横坐标和纵坐标的位置代表两个维度,气泡的大小则代表第三个维度。 在这个例子中,我们用numpy库生成了一些随机数据&a…...

视锥体裁剪射线的算法
射线Ray(直线情况)需要满足的条件: 在视野中显示的粗细均匀,需要分段绘制,每段的粗细根据到视野的距离计算射线model的顶点尽量少以节省性能损耗要满足条件2的话需要对射线进行裁剪,只绘制射线在视锥体内的部分,因此需要计算射线被视锥体裁剪后新的起点和终点 1. 计算三角…...
)
程序员在线周刊(投稿篇)
嗨,大家好!作为一名程序员,并且是一名互联网文章作者,我非常激动地向大家宣布,我们计划推出一份在线周刊,专门为程序员们提供有趣、实用的文章和资讯。而现在,我们正在征集投稿! 是…...
uniapp——实现聊天室功能——技能提升
这里写目录标题 效果图聊天室功能代码——html部分代码——js部分代码——其他部分 首先声明一点:下面的内容是从一个uniapp的程序中摘录的,并非本人所写,先做记录,以免后续遇到相似需求抓耳挠腮。 效果图 聊天室功能 发送图片 …...

脚本:用python实现五子棋
文章目录 1. 语言2. 效果3. 脚本4. 解读5. FutureReference 1. 语言 Python 无环境配置、无库安装。 2. 效果 以第一回合为例 玩家X 玩家0 3. 脚本 class GomokuGame:def __init__(self, board_size15):self.board_size board_sizeself.board [[ for _ in range(board_…...
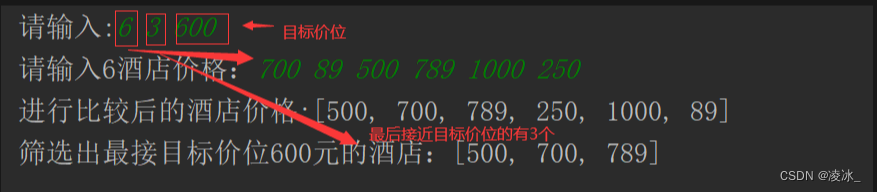
Java-华为真题-预定酒店
需求: 放暑假了,小王决定到某旅游景点游玩,他在网上搜索到了各种价位的酒店(长度为n的数组A),他的心理价位是x元,请帮他筛选出k个最接近x元的酒店(n>k>0)ÿ…...
win10 自带虚拟机软件 虚拟CentOS系统
win10 下使用需要虚拟一个系统,不需要额外安装VMware、Virtual box等软件。使用win10 自带虚拟机软件即可 步骤1 确保启动Hyper-V 功能启用 控制面板 -> 程序 -> 启用或关闭Windows功能 步骤 2 创建虚拟机 2.1 打开Typer-V 2.2 创建虚拟机 2.2.1 操作 -&g…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
