LeetCode 1584. 连接所有点的最小费用【最小生成树】
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个 points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
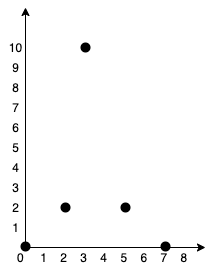
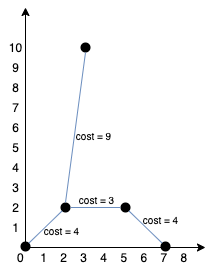
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出:20
解释:
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]]
输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]]
输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]]
输出:4000000
示例 5:
输入:points = [[0,0]]
输出:0
提示:
1 <= points.length <= 1000-
-10^6 <= xi, yi <= 10^6
- 所有点
(xi, yi)两两不同。
根据题意,我们得到了一张 O ( n ) O(n) O(n) 个节点的完全图,任意两点之间的距离均为它们的曼哈顿距离。现在我们需要在这个图中取得一个子图,恰满足子图的任意两点之间有且仅有一条简单路径,且这个子图的所有边的总权值之和尽可能小。
能够满足任意两点之间有且仅有一条简单路径只有树,且这棵树包含 O ( n ) O(n) O(n) 个节点。我们称这棵树为给定的图的生成树,其中总权值最小的生成树,我们称其为最小生成树。
解法 Kruskal算法
最小生成树有一个非常经典的解法: Kruskal \text{Kruskal} Kruskal 。 Kruskal \text{Kruskal} Kruskal 算法是一种常见并且好写的最小生成树算法,由 Kruskal \text{Kruskal} Kruskal 发明。该算法的基本思想是从小到大加入边,是一个贪心算法。
其算法流程为:
- 将图 G = { V , E } G=\{V,E\} G={V,E} 中的所有边按照长度由小到大进行排序,等长的边可以按任意顺序。
- 初始化图 G ′ G' G′ 为 { V , ∅ } \{V, \varnothing \} {V,∅} ,从前向后扫描排序后的边,如果扫描到的边 e e e 在 G ′ G' G′ 中连接了两个相异的连通块,则将它插入 G ′ G' G′ 中。
- 最后得到的图 G ′ G' G′ 就是图 G G G 的最小生成树。
在实际代码中,我们首先将这张完全图中的边全部提取到边集数组中(使用 struct 而非 vector<int> 存储每一条边,不然会超时,vector 的创建也需要一定时间),然后对所有边进行排序,从小到大进行枚举(当有了 n − 1 n - 1 n−1 条边后可提前退出对边集数组的扫描),每次贪心选边加入答案。使用并查集维护连通性,若当前边两端不连通即可选择这条边。
class Solution {
public:struct Edge {int i, j, w;};int minCostConnectPoints(vector<vector<int>>& points) {vector<Edge> edges;int n = points.size();for (int i = 0; i < n; ++i) {for (int j = 0; j < n; ++j) {int dx = abs(points[i][0] - points[j][0]);int dy = abs(points[i][1] - points[j][1]);edges.push_back({i, j, dx + dy});}}sort(edges.begin(), edges.end(), [&](const auto &a, const auto &b) {return a.w < b.w;});int total = 0;vector<int> fa(n, -1);function<int(int)> find = [&](int x) -> int { return fa[x] < 0 ? x : fa[x] = find(fa[x]); } ;auto merge = [&](int rx, int ry) {if (fa[rx] < fa[ry]) {fa[rx] += fa[ry];fa[ry] = rx;} else {fa[ry] += fa[rx];fa[rx] = ry;}};int num = 0;for (int i = 0; i < edges.size(); ++i) {int u = edges[i].i, v = edges[i].j;int ru = find(u), rv = find(v);if (ru != rv) {total += edges[i].w;merge(ru, rv);++num; // 边数到达了n-1时可以提前退出if (num == n - 1) break;}}return total;}
};
复杂度分析:
- 时间复杂度: O ( n 2 log ( n ) ) O(n^2\log(n)) O(n2log(n)) ,其中 O ( n ) O(n) O(n) 是节点数。一般 Kruskal \text{Kruskal} Kruskal 是 O ( m log m ) O(m\log m) O(mlogm) 的算法,但本题中 m = n 2 m=n^2 m=n2 ,因此总时间复杂度为 O ( n 2 log ( n ) ) O(n^2\log(n)) O(n2log(n)) 。
- 空间复杂度: O ( n 2 ) O(n^2) O(n2) ,其中 O ( n ) O(n) O(n) 是节点数。并查集使用 O ( n ) O(n) O(n) 的空间,边集数组需要使用 O ( n 2 ) O(n^2) O(n2) 的空间。
解法2 建图优化的 Kruskal \text{Kruskal} Kruskal
方法一中,虽然使用了 Kruskal \text{Kruskal} Kruskal 算法,但时间复杂度仍然较高,因为本题中的边数是 O ( n 2 ) O(n^2) O(n2) 的,所以我们需要想办法将减少边数。为此,我们提出几个结论:
结论一:对于图中的任意三点 A , B , C A,B,C A,B,C,假设边 A B , A C , B C AB,AC,BC AB,AC,BC 中 A B AB AB 为最长边,那么最终答案中必然不包含边 A B AB AB 。
我们利用反证法证明:假设最后答案中包含 A B AB AB ,那么此时 A C AC AC 与 B C BC BC 两边中至少有一条边是没有被选用的,我们总可以在保证连通性的情况下,将 A B AB AB 边替换为 A C AC AC 与 B C BC BC 两边中的某一个,使最小生成树的总权值变得更小。
结论二:对于下图中同属同一个区块的任意两点 B , C B,C B,C , A A A 为原点,那么 B C BC BC 不可能为三边中最长边。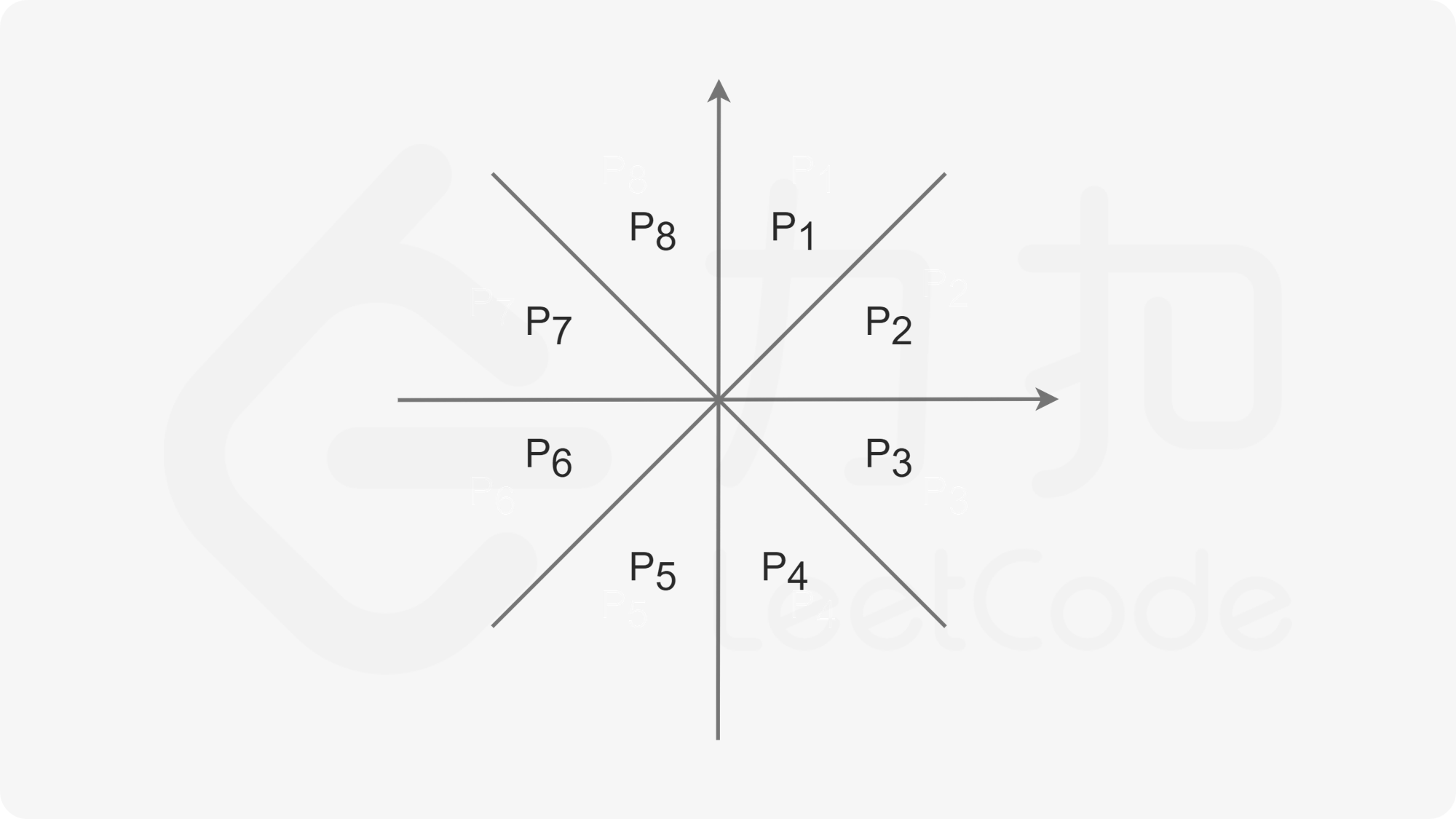
图中任意一个区块的两分割线的夹角均为 4 5 ∘ 45^\circ 45∘ 。我们以 P 1 P1 P1 区块为例,假设 B ( x B , y B ) , C ( x C , y C ) B(x_B,y_B),C(x_C,y_C) B(xB,yB),C(xC,yC) ,不失一般性,假设 x B + y B ≤ x C + y C x_B + y_B \leq x_C + y_C xB+yB≤xC+yC 。
因为处于 P 1 P1 P1 区域,所以有 0 ≤ x B ≤ y B 0 \leq x_B \leq y_B 0≤xB≤yB , 0 ≤ x C ≤ y C 0 \leq x_C \leq y_C 0≤xC≤yC 。所以 B C = ∣ x B − x C ∣ + ∣ y B − y C ∣ BC = |x_B - x_C| + |y_B - y_C| BC=∣xB−xC∣+∣yB−yC∣ 。下面我们尝试分类讨论:
- 当 x B > x C , y B > y C x_B > x_C, y_B > y_C xB>xC,yB>yC ,这与 x B + y B ≤ x C + y C x_B + y_B \leq x_C + y_C xB+yB≤xC+yC 矛盾。
- 当 x B ≤ x C , y B > y C x_B \leq x_C, y_B > y_C xB≤xC,yB>yC ,此时有 ∣ B C ∣ = x C − x B + y B − y C |BC| = x_C - x_B + y_B - y_C ∣BC∣=xC−xB+yB−yC , ∣ A C ∣ − ∣ B C ∣ = x C + y C − x C + x B − y B + y C = x B − y B + 2 × y C |AC| - |BC| = x_C + y_C - x_C + x_B - y_B + y_C = x_B - y_B + 2 \times y_C ∣AC∣−∣BC∣=xC+yC−xC+xB−yB+yC=xB−yB+2×yC 。由前面各种关系可得 y B > y C > x C > x B y_B > y_C > x_C > x_B yB>yC>xC>xB 。假设 ∣ A C ∣ < ∣ B C ∣ |AC| < |BC| ∣AC∣<∣BC∣ ,即 y B > 2 × y C + x B y_B > 2 \times y_C + x_B yB>2×yC+xB ,那么 ∣ A B ∣ = x B + y B > 2 × x B + 2 × y C |AB| = x_B + y_B > 2 \times x_B + 2 \times y_C ∣AB∣=xB+yB>2×xB+2×yC , ∣ A C ∣ = x C + y C < 2 × y C < ∣ A B ∣ |AC| = x_C + y_C < 2 \times y_C < |AB| ∣AC∣=xC+yC<2×yC<∣AB∣ 与前提矛盾,故 ∣ A C ∣ ≥ ∣ B C ∣ |AC| \geq |BC| ∣AC∣≥∣BC∣ ;
- x B > x C x_B> x_C xB>xC 且 y B ≤ y c y_B \leq y_c yB≤yc 。与 2 同理;
- x B ≤ x C x_B \leq x_C xB≤xC 且 y B ≤ y C y_B \leq y_C yB≤yC 。此时显然有 ∣ A B ∣ + ∣ B C ∣ = ∣ A C ∣ |AB| + |BC| = |AC| ∣AB∣+∣BC∣=∣AC∣ ,即有 ∣ A C ∣ > ∣ B C ∣ |AC| > |BC| ∣AC∣>∣BC∣ 。
综上有 ∣ A C ∣ ≥ ∣ B C ∣ |AC| \geq |BC| ∣AC∣≥∣BC∣ ,这个性质可以从 P 1 P1 P1 区域推导到其他七个区域。
结论三:假设存在一点 A A A 在原点处,那么对于图中的任意一个 4 5 ∘ 45^\circ 45∘ 区域,我们都至多只选择其中的一个点与 A A A 相连,且该点必然为该区域中距离 A A A 最近的点。
我们首先利用反证法证明:假设最后答案中包含 A B AB AB 与 A C AC AC,且 B B B 与 C C C 均位于同一个 4 5 ∘ 45^\circ 45∘ 区域中。那么由结论二可知, B C BC BC 必不为三边中的最长边。即最长边必然为 A B AB AB 或 A C AC AC 。由结论一可知, A B AB AB 与 A C AC AC 中必然有一个不包含在答案中,这与假设相悖,因此我们最多仅会选择一个点与 A A A 相连。
我们进一步思考,既然最多仅会选择一个点与 A A A 相连,且三边中的最长边不为 A A A 的对边,那么仅有距离 A A A 最近的点与 A A A 所连的边可能出现在答案中。证毕。
依据结论三我们可以知道,一个点至多连八条边,因此我们至多只需要连出 O ( n ) O(n) O(n) 条边。
细节:为防止重复连边,我们对每一个点只考虑对 P 1 , P 2 , P 3 , P 4 P1,P2,P3,P4 P1,P2,P3,P4 连边的情况,假设 A A A 点坐标为 ( x , y ) (x,y) (x,y) ,对于这四个点,我们可以概括为:
- 对于 P 1 P1 P1 区域的 ( x 1 , y 1 ) (x_1,y_1) (x1,y1) ,有 x 1 ≥ x , y 1 − x 1 ≥ y − x x_1 \geq x, y_1 - x_1 \geq y - x x1≥x,y1−x1≥y−x ,其中最近点的 x 1 + y 1 x_1 + y_1 x1+y1 最小。
- 对于 P 2 P2 P2 区域的 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) ,有 y 2 ≥ y , y 2 − x 2 ≤ y − x y_2 \geq y, y_2 - x_2 \leq y - x y2≥y,y2−x2≤y−x ,其中最近点的 x 2 + y 2 x_2 + y_2 x2+y2 最小。
- 对于 P 3 P3 P3 区域的 ( x 3 , y 3 ) (x_3,y_3) (x3,y3) ,有 y 3 ≤ y , y 3 + x 3 ≥ y + x y_3 \leq y, y_3 + x_3 \geq y + x y3≤y,y3+x3≥y+x ,其中最近点的 y 3 − x 3 y_3 - x_3 y3−x3 最小。
- 对于 P 4 P4 P4 区域的 ( x 4 , y 4 ) (x_4,y_4) (x4,y4) ,有 x 4 ≥ x , y 4 + x 4 ≤ y + x x_4 \geq x, y_4 + x_4 \leq y + x x4≥x,y4+x4≤y+x ,其中最近点的 y 4 − x 4 y_4 - x_4 y4−x4 最小。
这样,我们分别处理每一个区域即可,以 P 1 P1 P1 区域为例,我们先通过排序使得所有点按照横坐标从大到小排列,然后将每一个点的 y i − x i y_i - x_i yi−xi 信息记录,将离散化后记录在数组的下标为 y i − x i y_i - x_i yi−xi 的位置中,并利用树状数组维护该数组的前缀最小值。这样我们就可以动态地、单次 O ( log n ) O(\log n) O(logn) 地计算每个点的 P 1 P1 P1 区域所选择的点。
为了提升编码效率,实际代码中我们只实现了 P 1 P1 P1 区域的算法,对于其它三个区域,我们通过巧妙的坐标变化使其条件变为 P 1 P1 P1 区域,使得代码能够更加高效地复用。
class DisjointSetUnion {
private:vector<int> f, rank;int n;public:DisjointSetUnion(int _n) {n = _n;rank.resize(n, 1);f.resize(n);for (int i = 0; i < n; i++) {f[i] = i;}}int find(int x) {return f[x] == x ? x : f[x] = find(f[x]);}int unionSet(int x, int y) {int fx = find(x), fy = find(y);if (fx == fy) {return false;}if (rank[fx] < rank[fy]) {swap(fx, fy);}rank[fx] += rank[fy];f[fy] = fx;return true;}
};class BIT {
public:vector<int> tree, idRec;int n;BIT(int _n) {n = _n;tree.resize(n, INT_MAX);idRec.resize(n, -1);}int lowbit(int k) {return k & (-k);}void update(int pos, int val, int id) {while (pos > 0) {if (tree[pos] > val) {tree[pos] = val;idRec[pos] = id;}pos -= lowbit(pos);}}int query(int pos) {int minval = INT_MAX;int j = -1;while (pos < n) {if (minval > tree[pos]) {minval = tree[pos];j = idRec[pos];}pos += lowbit(pos);}return j;}
};struct Edge {int len, x, y;Edge(int len, int x, int y) : len(len), x(x), y(y) {}bool operator<(const Edge& a) const {return len < a.len;}
};struct Pos {int id, x, y;bool operator<(const Pos& a) const {return x == a.x ? y < a.y : x < a.x;}
};class Solution {
public:vector<Edge> edges;vector<Pos> pos;void build(int n) {sort(pos.begin(), pos.end());vector<int> a(n), b(n);for (int i = 0; i < n; i++) {a[i] = pos[i].y - pos[i].x;b[i] = pos[i].y - pos[i].x;}sort(b.begin(), b.end());b.erase(unique(b.begin(), b.end()), b.end());int num = b.size();BIT bit(num + 1);for (int i = n - 1; i >= 0; i--) {int poss = lower_bound(b.begin(), b.end(), a[i]) - b.begin() + 1;int j = bit.query(poss);if (j != -1) {int dis = abs(pos[i].x - pos[j].x) + abs(pos[i].y - pos[j].y);edges.emplace_back(dis, pos[i].id, pos[j].id);}bit.update(poss, pos[i].x + pos[i].y, i);}}void solve(vector<vector<int>>& points, int n) {pos.resize(n);for (int i = 0; i < n; i++) {pos[i].x = points[i][0];pos[i].y = points[i][1];pos[i].id = i;}build(n);for (int i = 0; i < n; i++) {swap(pos[i].x, pos[i].y);}build(n);for (int i = 0; i < n; i++) {pos[i].x = -pos[i].x;}build(n);for (int i = 0; i < n; i++) {swap(pos[i].x, pos[i].y);}build(n);}int minCostConnectPoints(vector<vector<int>>& points) {int n = points.size();solve(points, n);DisjointSetUnion dsu(n);sort(edges.begin(), edges.end());int ret = 0, num = 1;for (auto& [len, x, y] : edges) {if (dsu.unionSet(x, y)) {ret += len;num++;if (num == n) {break;}}}return ret;}
};
复杂度分析:
- 时间复杂度: O ( n log n ) O(n\log n) O(nlogn) ,其中 O ( n ) O(n) O(n) 是节点数。预处理建边的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn) ,因为需要排序,以及使用树状数组维护。在只有 O ( n ) O(n) O(n) 条边的情况下, Kruskal \text{Kruskal} Kruskal 的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn) ,因此总时间复杂度为 O ( n log n ) O(n\log n) O(nlogn) 。
- 空间复杂度: O ( n ) O(n) O(n),其中 O ( n ) O(n) O(n) 是节点数。树状数组,并查集、离散化以及边集数组都只使用 O ( n ) O(n) O(n) 的空间。
加粗样式
相关文章:

LeetCode 1584. 连接所有点的最小费用【最小生成树】
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

超简单,几行js代码就实现一个 vue3 的数字滚动效果!
预览效果 1. 创建一个template <template><div class"num-warp"><template v-for"item in numStr"><div v-if"item ," class"dot">,</div><divv-elseclass"num-box":style"{transf…...
两阶段鲁棒优化matlab实现——CCG和benders
目录 1 主要内容 2 部分代码 3 程序结果 4 程序链接 1 主要内容 程序采用matlab复现经典论文《Solving two-stage robust optimization problems using a column-and-constraint generation method》算例,实现了C&CG和benders算法两部分内容,通过…...

二进制安全虚拟机Protostar靶场(4)写入shellcode,基础知识讲解 Stack Five
前言 这是一个系列文章,之前已经介绍过一些二进制安全的基础知识,这里就不过多重复提及,不熟悉的同学可以去看看我之前写的文章 二进制安全虚拟机Protostar靶场 安装,基础知识讲解,破解STACK ZERO https://blog.csdn.net/qq_45894840/artic…...
【Flink实战】玩转Flink里面核心的Source Operator实战
🚀 作者 :“大数据小禅” 🚀 文章简介 :【Flink实战】玩转Flink里面核心的Source Operator实战 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 目录导航 Flink 的API层级介绍Source Operator速览Flin…...

[2023-09-12]Oracle备库查询报ORA-01187
一个多表关联的语句在备库执行查询时提示ORA-01187: cannot read from file because it failed verification tests,单独对某一个表查询则正常返回(因为不需要排序等,没有用到临时表空间)。 查看报错信息发现是提示的临时数据文件…...

leetcode 16.最接近的三数之和
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 示例 1: 输入:nums [-1,2,1,-4], target 1 输出:…...

antd table 自定义排序图标
要在Ant Design的Table组件中自定义排序图标,可以使用sorter和sortDirections属性来实现自定义排序逻辑和图标。以下是一个示例,演示如何在Ant Design的Table中自定义排序图标: import React, { useState } from react; import { Table, Spa…...
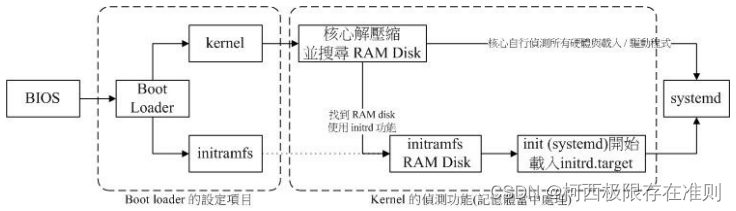
第十九章、【Linux】开机流程、模块管理与Loader
19.1.1 开机流程一览 以个人计算机架设的 Linux 主机为例,当你按下电源按键后计算机硬件会主动的读取 BIOS 或 UEFI BIOS 来载入硬件信息及进行硬件系统的自我测试, 之后系统会主动的去读取第一个可开机的设备 (由 BIOS 设置的) …...
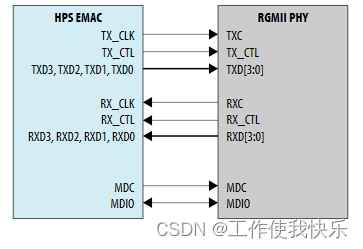
GMAC PHY介绍
1.1PHY接口发展 (1)MII支持10M/100Mbps,一个接口由14根线组成,它的支持还是比较灵活的,但是有一个缺点是因为它一个端口用的信号线太多。参考芯片:DP83848 、DM900A(该芯片内部集成了MAC和PHY接…...

华为OD机考算法题:最远足迹
目录 题目部分 解读与分析 代码实现 题目部分 题目最远足迹难度易题目说明某探险队负责对地下洞穴进行探险。 探险队成员在进行探险任务时,随身携带的记录器会不定期地记录自身的坐标,但在记录的间隙中也会记录其他数据。探索工作结束后,…...

QScrollBar滚动条、QSlider滑块、 QDial表盘
QAbstractSlider 类、 QSCrollBar 类、 QSlider 类 一、 基本原理 1、 QAbstractSlider 继承自 QWidget,该类主要用于提供一个范围内的整数值, 2、 QAbstractSlider 类是 QScrollBar 类(滚动条)、 QSlider 类(滑块)、 QDial 类(表盘)的父类,因…...
Prometheus+Grafana可视化监控【MySQL状态】
文章目录 一、安装Docker二、安装MySQL数据库(Docker容器方式)三、安装Prometheus四、安装Grafana五、Pronetheus和Grafana相关联六、安装mysqld_exporter七、Grafana添加MySQL监控模板 一、安装Docker 注意:我这里使用之前写好脚本进行安装Docker,如果…...
)
五,编译定制rom并刷机实现硬改(二)
系列文章目录 第一章 安卓aosp源码编译环境搭建 第二章 手机硬件参数介绍和校验算法 第三章 修改安卓aosp代码更改硬件参数 第四章 编译定制rom并刷机实现硬改(一) 第五章 编译定制rom并刷机实现硬改(二) 第六章 不root不magisk不xposed lsposed frida原生修改定位 第七章 安卓…...

Modbus协议详解3:数据帧格式 - RTU帧 ASCII帧的区别
Modbus既然是一种通信协议,那它就应该有规定的通信格式用于在设备之间的指令接收与识别。 本文就着重讲讲Modbus协议的RTU帧和ASCII帧。 Modbus帧在串行链路上的格式如下: 在上图的格式中: 1)地址域:指代的是子节点地址…...

认识数据分析
文章目录 1. 认识数据分析1.1 数据自身的三大属性1.2 建数仓 数据分析的工程技术1.3 数据分析解决问题的原理1.4 数据分析的具体流程1.5 数据的中心化和智能化1.6 数据分析的四种类型和六个方向 1. 认识数据分析 1.1 数据自身的三大属性 客观:用数字衡量和表现一件…...

Learn Prompt-ChatGPT 精选案例:写作博客
在 ChatGPT 的帮助下,文本内容的产出,尤其是撰写博客文章的过程得到了进一步的简化。你可以让 ChatGPT 激发你的灵感,也可以让它美化你的文章内容。 这里我们希望能通过prompt写出一篇以“ChatGPT对社会各行各业的影响”为主题的博客。 本页…...

《确保安全:PostgreSQL安全配置与最佳实践》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

Unity中Shader抓取屏幕并实现扭曲效果
文章目录 前言一、屏幕抓取,在上一篇文章已经写了二、实现抓取后的屏幕扭曲实现思路:1、屏幕扭曲要借助传入 UV 贴图进行扭曲2、传入贴图后在顶点着色器的输入参数处,传入一个 float2 uv : TEXCOORD,用于之后对扭曲贴图进行采样3、…...

深浅拷贝详解
深浅拷贝 经典真题 深拷贝和浅拷贝的区别?如何实现 深拷贝和浅拷贝概念 首先,我们需要明确深拷贝和浅拷贝的概念。 浅拷贝:只是拷贝了基本类型的数据,而引用类型数据,复制后也是会发生引用,我们把这种拷…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...
