游戏开发初等数学基础
凑数图()
立体图形面积体积
1. 立方体(Cube):
- 表面积公式: 6 a 2 6a^2 6a2 (其中 a a a 是边长)。
- 体积公式: a 3 a^3 a3 (其中 a a a 是边长)。
2. 球体(Sphere):
- 表面积公式: 4 π r 2 4\pi r^2 4πr2 (其中 r r r 是半径)。
- 体积公式: 4 3 π r 3 \frac{4}{3}\pi r^3 34πr3 (其中 r r r 是半径)。
3. 圆柱体(Cylinder):
- 表面积公式(侧面和两个底面总和): 2 π r h + 2 π r 2 2\pi rh + 2\pi r^2 2πrh+2πr2 (其中 r r r 是底面半径, h h h 是高度)。
- 体积公式: π r 2 h \pi r^2h πr2h (其中 r r r 是底面半径, h h h 是高度)。
4. 锥体(Cone):
- 表面积公式(侧面和底面总和): π r ( r + r 2 + h 2 ) \pi r(r + \sqrt{r^2 + h^2}) πr(r+r2+h2) (其中 r r r 是底面半径, h h h 是高度)。
- 体积公式: 1 3 π r 2 h \frac{1}{3}\pi r^2h 31πr2h (其中 r r r 是底面半径, h h h 是高度)。
5. 圆环(Torus):
- 表面积公式: 4 π 2 R r 4\pi^2 Rr 4π2Rr (其中 R R R 是大半径, r r r 是小半径)。
- 体积公式: 2 π 2 R r 2 2\pi^2 Rr^2 2π2Rr2 (其中 R R R 是大半径, r r r 是小半径)。
平面图形面积与周长
1. 矩形(Rectangle):
- 面积公式: A = l ⋅ w A = l \cdot w A=l⋅w (其中 l l l 是长度, w w w 是宽度)。
- 周长公式: P = 2 ( l + w ) P = 2(l + w) P=2(l+w) (其中 l l l 是长度, w w w 是宽度)。
2. 正方形(Square):
- 面积公式: A = a 2 A = a^2 A=a2 (其中 a a a 是边长)。
- 周长公式: P = 4 a P = 4a P=4a (其中 a a a 是边长)。
3. 圆(Circle):
- 面积公式: A = π r 2 A = \pi r^2 A=πr2 (其中 r r r 是半径)。
- 周长公式: P = 2 π r P = 2\pi r P=2πr (其中 r r r 是半径)。
4. 三角形(Triangle):
- 面积公式: A = 1 2 b h A = \frac{1}{2}bh A=21bh (其中 b b b 是底边长, h h h 是高度)。
- 周长公式: P = a + b + c P = a + b + c P=a+b+c (其中 a a a、 b b b、 c c c 是三边长度)。
5. 梯形(Trapezoid):
- 面积公式: A = 1 2 ( a + b ) h A = \frac{1}{2}(a + b)h A=21(a+b)h (其中 a a a 和 b b b 是上下底边长, h h h 是高度)。
- 周长公式: P = a + b + c + d P = a + b + c + d P=a+b+c+d (其中 a a a、 b b b、 c c c、 d d d 是各边长度)。
6. 圆环(Annulus):
- 面积公式: A = π ( R 2 − r 2 ) A = \pi(R^2 - r^2) A=π(R2−r2) (其中 R R R 是外圆半径, r r r 是内圆半径)。
- 周长公式: P = 2 π ( R + r ) P = 2\pi(R + r) P=2π(R+r) (其中 R R R 是外圆半径, r r r 是内圆半径)。
三角函数
1. 两角相加的三角函数公式:
- sin ( A + B ) = sin ( A ) cos ( B ) + cos ( A ) sin ( B ) \sin(A + B) = \sin(A)\cos(B) + \cos(A)\sin(B) sin(A+B)=sin(A)cos(B)+cos(A)sin(B)
- cos ( A + B ) = cos ( A ) cos ( B ) − sin ( A ) sin ( B ) \cos(A + B) = \cos(A)\cos(B) - \sin(A)\sin(B) cos(A+B)=cos(A)cos(B)−sin(A)sin(B)
- tan ( A + B ) = tan ( A ) + tan ( B ) 1 − tan ( A ) tan ( B ) \tan(A + B) = \frac{\tan(A) + \tan(B)}{1 - \tan(A)\tan(B)} tan(A+B)=1−tan(A)tan(B)tan(A)+tan(B)
2. 两角差的三角函数公式:
- sin ( A − B ) = sin ( A ) cos ( B ) − cos ( A ) sin ( B ) \sin(A - B) = \sin(A)\cos(B) - \cos(A)\sin(B) sin(A−B)=sin(A)cos(B)−cos(A)sin(B)
- cos ( A − B ) = cos ( A ) cos ( B ) + sin ( A ) sin ( B ) \cos(A - B) = \cos(A)\cos(B) + \sin(A)\sin(B) cos(A−B)=cos(A)cos(B)+sin(A)sin(B)
- tan ( A − B ) = tan ( A ) − tan ( B ) 1 − tan ( A ) tan ( B ) \tan(A - B) = \frac{\tan(A) - \tan(B)}{1 - \tan(A)\tan(B)} tan(A−B)=1−tan(A)tan(B)tan(A)−tan(B)
3. 二重角的三角函数公式:
- sin ( 2 A ) = 2 sin ( A ) cos ( A ) \sin(2A) = 2\sin(A)\cos(A) sin(2A)=2sin(A)cos(A)
- cos ( 2 A ) = cos 2 ( A ) − sin 2 ( A ) = 2 cos 2 ( A ) − 1 = 1 − 2 sin 2 ( A ) \cos(2A) = \cos^2(A) - \sin^2(A) = 2\cos^2(A) - 1 = 1 - 2\sin^2(A) cos(2A)=cos2(A)−sin2(A)=2cos2(A)−1=1−2sin2(A)
- tan ( 2 A ) = 2 tan ( A ) 1 − tan 2 ( A ) \tan(2A) = \frac{2\tan(A)}{1 - \tan^2(A)} tan(2A)=1−tan2(A)2tan(A)
4. 半角的三角函数公式:
- sin ( A 2 ) = ± 1 − cos ( A ) 2 \sin\left(\frac{A}{2}\right) = \pm\sqrt{\frac{1 - \cos(A)}{2}} sin(2A)=±21−cos(A)
- cos ( A 2 ) = ± 1 + cos ( A ) 2 \cos\left(\frac{A}{2}\right) = \pm\sqrt{\frac{1 + \cos(A)}{2}} cos(2A)=±21+cos(A)
- tan ( A 2 ) = ± 1 − cos ( A ) 1 + cos ( A ) \tan\left(\frac{A}{2}\right) = \pm\sqrt{\frac{1 - \cos(A)}{1 + \cos(A)}} tan(2A)=±1+cos(A)1−cos(A)
5. 和差化积公式:
- sin ( A ) sin ( B ) = 1 2 [ cos ( A − B ) − cos ( A + B ) ] \sin(A)\sin(B) = \frac{1}{2}[\cos(A - B) - \cos(A + B)] sin(A)sin(B)=21[cos(A−B)−cos(A+B)]
- cos ( A ) cos ( B ) = 1 2 [ cos ( A − B ) + cos ( A + B ) ] \cos(A)\cos(B) = \frac{1}{2}[\cos(A - B) + \cos(A + B)] cos(A)cos(B)=21[cos(A−B)+cos(A+B)]
- sin ( A ) cos ( B ) = 1 2 [ sin ( A − B ) + sin ( A + B ) ] \sin(A)\cos(B) = \frac{1}{2}[\sin(A - B) + \sin(A + B)] sin(A)cos(B)=21[sin(A−B)+sin(A+B)]
6. 和差化积公式的反函数:
- sin ( A + B ) = 2 sin ( A + B 2 ) cos ( A − B 2 ) \sin(A + B) = 2\sin\left(\frac{A + B}{2}\right)\cos\left(\frac{A - B}{2}\right) sin(A+B)=2sin(2A+B)cos(2A−B)
- sin ( A − B ) = 2 sin ( A − B 2 ) cos ( A + B 2 ) \sin(A - B) = 2\sin\left(\frac{A - B}{2}\right)\cos\left(\frac{A + B}{2}\right) sin(A−B)=2sin(2A−B)cos(2A+B)
- cos ( A + B ) = 2 cos ( A + B 2 ) cos ( A − B 2 ) \cos(A + B) = 2\cos\left(\frac{A + B}{2}\right)\cos\left(\frac{A - B}{2}\right) cos(A+B)=2cos(2A+B)cos(2A−B)
- cos ( A − B ) = − 2 sin ( A + B 2 ) sin ( A − B 2 ) \cos(A - B) = -2\sin\left(\frac{A + B}{2}\right)\sin\left(\frac{A - B}{2}\right) cos(A−B)=−2sin(2A+B)sin(2A−B)
向量
1. 向量加法和减法:
- 加法公式:对于两个向量 a ( x 1 , y 1 ) \mathbf{a}(x_1,y_1) a(x1,y1) 和 b ( x 2 , y 2 ) \mathbf{b}(x_2,y_2) b(x2,y2),它们的和为 c ( x 1 + x 2 , y 1 + y 2 ) \mathbf{c}(x_1+x_2,y_1+y_2) c(x1+x2,y1+y2),即 c = a + b \mathbf{c} = \mathbf{a} + \mathbf{b} c=a+b。
- 减法公式:对于两个向量 a ( x 1 , y 1 ) \mathbf{a}(x_1,y_1) a(x1,y1) 和 b ( x 2 , y 2 ) \mathbf{b}(x_2,y_2) b(x2,y2),它们的和为 c ( x 1 − x 2 , y 1 − y 2 ) \mathbf{c}(x_1-x_2,y_1-y_2) c(x1−x2,y1−y2),即 c = a − b \mathbf{c} = \mathbf{a} - \mathbf{b} c=a−b。
2. 向量数量乘法:
- 数乘公式:对于向量 a \mathbf{a} a 和标量 k k k, k k k 乘以向量 a \mathbf{a} a 的每个分量,即 k a k\mathbf{a} ka,得到一个新的向量。
3. 点积(内积):
- 点积公式:对于两个向量 a \mathbf{a} a 和 b \mathbf{b} b,它们的点积为 a ⋅ b = ∣ a ∣ ∣ b ∣ cos ( θ ) \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos(\theta) a⋅b=∣a∣∣b∣cos(θ),其中 ∣ a ∣ |\mathbf{a}| ∣a∣ 和 ∣ b ∣ |\mathbf{b}| ∣b∣ 分别是向量 a \mathbf{a} a 和 b \mathbf{b} b 的模长, θ \theta θ 是它们之间的夹角。
- 性质:
- 对于平行向量,点积为正, cos ( θ ) = 1 \cos(\theta) = 1 cos(θ)=1。
- 对于垂直向量,点积为零, cos ( θ ) = 0 \cos(\theta) = 0 cos(θ)=0。
- 点积具有交换律: a ⋅ b = b ⋅ a \mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a} a⋅b=b⋅a。
- 点积具有分配律: a ⋅ ( b + c ) = a ⋅ b + a ⋅ c \mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c} a⋅(b+c)=a⋅b+a⋅c。
- 用途:
-
计算夹角:点乘可用于计算两个向量之间的夹角。具体地,两个向量 a \mathbf{a} a 和 b \mathbf{b} b 的点乘 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 等于它们的模长之积与夹角的余弦值的乘积: a ⋅ b = ∣ a ∣ ∣ b ∣ cos ( θ ) \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos(\theta) a⋅b=∣a∣∣b∣cos(θ)。这可用于判断两个向量的相对方向,例如是否平行、垂直或是在一般的夹角。
-
投影:点乘可用于计算一个向量在另一个向量上的投影。通过将一个向量 a \mathbf{a} a 投影到另一个向量 b \mathbf{b} b 上,可以得到 a \mathbf{a} a 在 b \mathbf{b} b 方向上的分量,其大小为 a ⋅ b / ∣ b ∣ \mathbf{a} \cdot \mathbf{b} / |\mathbf{b}| a⋅b/∣b∣。
-
工作、能量和功率:点乘在物理学中用于计算力和位移之间的功和能量。力在方向上的分量乘以位移等于所做的功。
-
4. 叉积(外积):
-
叉积公式:对于两个三维向量 a \mathbf{a} a 和 b \mathbf{b} b,它们的叉积 a × b \mathbf{a} \times \mathbf{b} a×b 的计算方式如下:
a × b = ∣ i j k a 1 a 2 a 3 b 1 b 2 b 3 ∣ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} a×b= ia1b1ja2b2ka3b3
其中,ijk分别表示xyz三个轴的基本单位向量,通常我们并不关注。这可以通过展开行列式来计算,结果是一个新的向量,其分量为 c 1 c_1 c1、 c 2 c_2 c2 和 c 3 c_3 c3。
-
分量计算:根据行列式展开, c 1 c_1 c1、 c 2 c_2 c2 和 c 3 c_3 c3 分别计算如下:
c 1 = a 2 b 3 − a 3 b 2 c_1 = a_2 b_3 - a_3 b_2 c1=a2b3−a3b2
c 2 = a 3 b 1 − a 1 b 3 c_2 = a_3 b_1 - a_1 b_3 c2=a3b1−a1b3
c 3 = a 1 b 2 − a 2 b 1 c_3 = a_1 b_2 - a_2 b_1 c3=a1b2−a2b1 -
性质:
- 叉积的结果是垂直于 a \mathbf{a} a 和 b \mathbf{b} b 的向量。
- 叉积的模长等于 a \mathbf{a} a 和 b \mathbf{b} b 构成的平行四边形的面积。
- 叉积具有反交换律: a × b = − ( b × a ) \mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a}) a×b=−(b×a)。
- 叉积具有分配律: a × ( b + c ) = a × b + a × c \mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c} a×(b+c)=a×b+a×c。
-
作用:
-
法向量:叉乘可用于计算平面上三个点或三个向量所确定的平面的法向量。对于两个向量 a \mathbf{a} a 和 b \mathbf{b} b 的叉乘 a × b \mathbf{a} \times \mathbf{b} a×b,结果是一个垂直于 a \mathbf{a} a 和 b \mathbf{b} b 平面的向量,其方向遵循右手定则。
-
面积:叉乘的模长等于两个向量所张成的平行四边形(或平行四边形的面积)的面积。这在计算几何学中非常有用。
-
角动量和扭矩:在物理学和工程学中,叉乘用于计算角动量和扭矩(力矩)。角动量是物体旋转时的动力学性质,而扭矩用于描述力对物体的旋转作用。
-
电磁学中的洛伦兹力:在电磁学中,洛伦兹力的计算涉及电荷、电场和磁场之间的叉乘关系。
-
右手定则
a. 伸开你的右手,将大拇指、食指和中指垂直伸出,使它们呈 90 度角。
b. 让大拇指指向第一个输入向量 a \mathbf{a} a 的方向。
c. 让食指指向第二个输入向量 b \mathbf{b} b 的方向。
d. 你的中指所指向的方向就是结果法向量 n \mathbf{n} n 的方向。
e. 方向的确定是根据右手的构型而来,所以它遵循右手定则。
5. 混合积(三重积):
- 混合积公式:对于三个向量 a \mathbf{a} a、 b \mathbf{b} b 和 c \mathbf{c} c,它们的混合积为 a ⋅ ( b × c ) \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) a⋅(b×c)。混合积表示了这三个向量所构成的平行六面体的有向体积。
- 性质:
- 混合积的绝对值等于平行六面体的体积。
- 混合积可以用来判断三个向量是否共面,如果混合积为零,它们共面。
相关文章:

游戏开发初等数学基础
凑数图() 立体图形面积体积 1. 立方体(Cube): 表面积公式: 6 a 2 6a^2 6a2 (其中 a a a 是边长)。体积公式: a 3 a^3 a3 (其中 a a a 是边长)。 2. 球体(Sphere): 表面积公…...

svg图片代码data:image/svg+xml转png图片方法
把代码保存为html格式的文件中,用浏览器访问,即可右键保存 从AI软件或其它网站得到svg图片代码后,把他复制到下面源码上 注意:src""图片地址中,一些参数的含义 d‘这里是图片代码数据’ viewBox是图片显示区域,宽,高等 fill%23000000’这里表示颜色 ,后面6位0表示黑色…...

解决问题:Replace `‘vue‘;⏎` with `“vue“;`
使用vscode写vue文件的问题: Replace vue;⏎ with "vue"; error Replace v-model:value"xxx"placeholder"inputsearch prettier/prettier 7:38 error Insert ⏎ potentially fixable with the --fix option 原因:格式问题&a…...
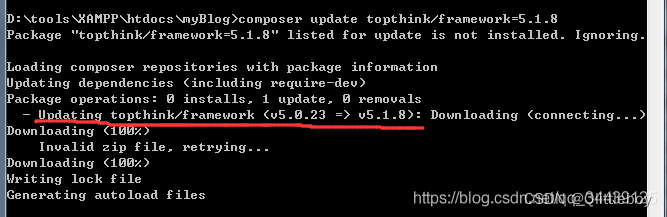
ThinkPHP 5.0通过composer升级到5.1,超级简单
事情是这样的,我实现一个验证码登录的功能,但是这个验证码的包提示tp5的版本可以是5.1.1、5.1.2、5.1.3。但我使用的是5.0,既然这样,那就升个级呗,百度了一下,结果发现大部分都是讲先备份application和修改…...
计算机竞赛 多目标跟踪算法 实时检测 - opencv 深度学习 机器视觉
文章目录 0 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习多目标跟踪 …...

一文了解大模型工作原理——以ChatGPT为例
文章目录 写在前面1.Tansformer架构模型2.ChatGPT原理3.提示学习与大模型能力的涌现3.1 提示学习3.2 上下文学习3.3 思维链 4.行业参考建议4.1 拥抱变化4.2 定位清晰4.3 合规可控4.4 经验沉淀 写在前面 2022年11月30日,ChatGPT模型问世后,立刻在全球范围…...

CPP-Templates-2nd--第十九章 萃取的实现 19.7---
目录 19.7 其它的萃取技术 19.7.1 If-Then-Else 19.7.2 探测不抛出异常的操作 19.7.3 萃取的便捷性(Traits Convenience) 别名模板和萃取(Alias Templates And Traits) 变量模板和萃取(Variable Templates and Traits&…...
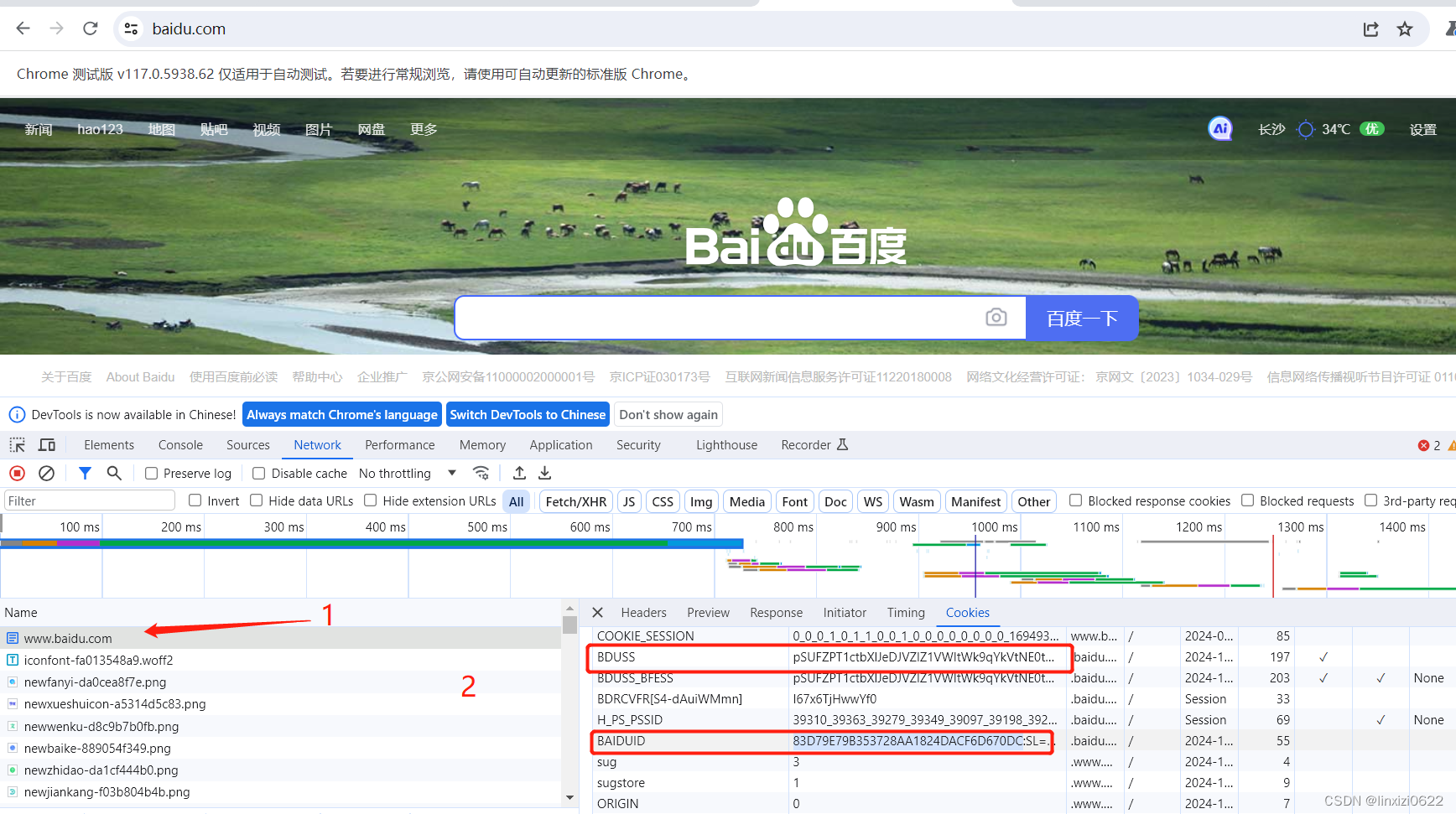
python 采用selenium+cookies 获取登录后的网页
百度网页由于需要登陆手机短信验证。比较麻烦 这里我采用先人工登录百度账号,然后将百度账号的相关cookies保存下来 然后采用selenium动态登录网页 整体代码如下 from selenium import webdriverimport timeoptions webdriver.ChromeOptions()options.add_argu…...

【测试开发】答疑篇 · 什么是软件测试
【测试开发】答疑篇 文章目录 【测试开发】答疑篇1. 生活中的测试2. 什么是软件测试3. 为什么要有测试/没有测试行不行4. 软件测试和软件开发的区别5. 软件测试和软件调试之间的区别6. 软件测试的岗位7. 优秀测试人员具备的素质 【测试开发】答疑篇 软件不一定是桌面应用&#…...
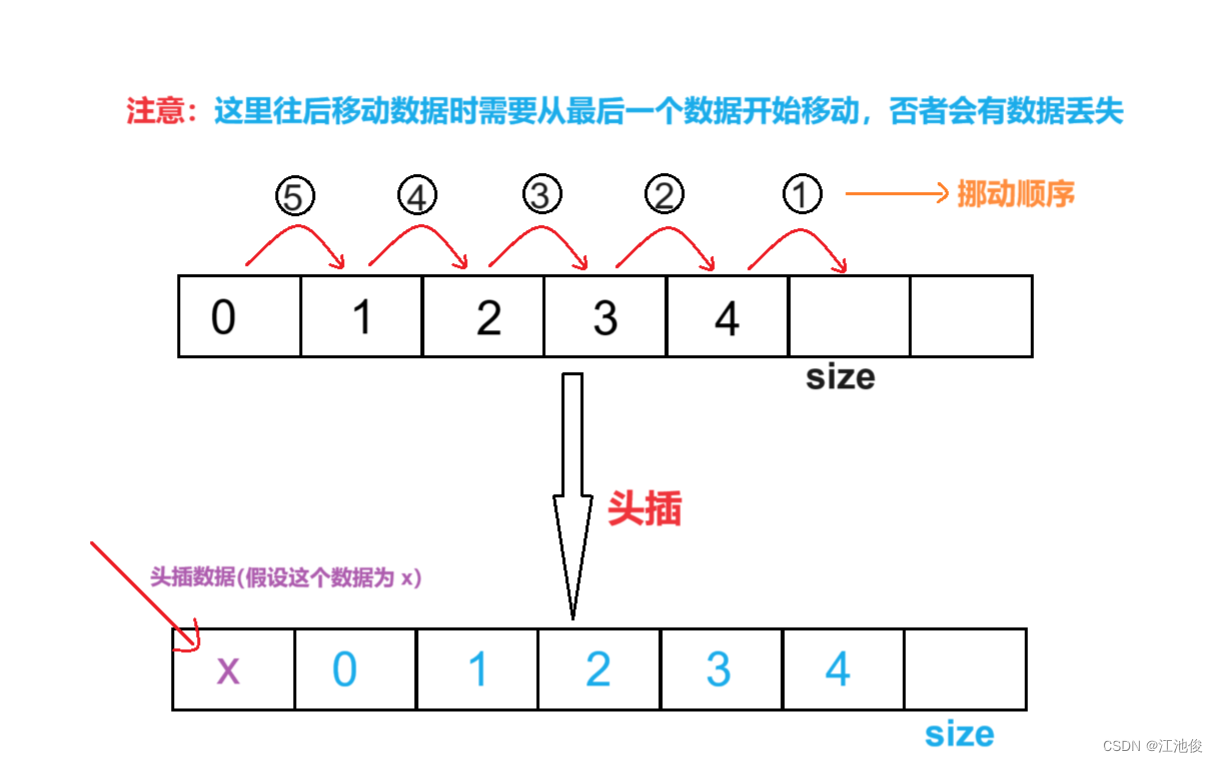
深入解析顺序表:揭开数据结构的奥秘,掌握顺序表的精髓
💓 博客主页:江池俊的博客⏩ 收录专栏:数据结构探索👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路💻代码仓库:江池俊的代码仓库🔥编译环境:Visual Studio 2022Ἰ…...

数据风险量化评估方案
一、企业面临数据安全的痛点 1、企业缺少清晰的数据安全意识 各部门重视度不够,缺少主动数据安全管控意识。数据安全管控架构不清晰,职责划分不明确。对数据安全管控认识不全面、不深刻。工作人员对于所持有的数据缺乏概念,导致数据的价值无…...

EasyAVFilter代码示例之将视频点播文件转码成HLS(m3u8+ts)视频点播格式
以下是一套完整的视频点播功能开发源码,就简简单单几行代码,就可以完成原来ffmpeg很复杂的视频点播转码调用流程,而且还可以集成在自己的应用程序中调用,例如java、php、cgo、c、nodejs,不需要再单独一个ffmpeg的进程来…...
动态规划 part 11)
day-50 代码随想录算法训练营(19)动态规划 part 11
123.买卖股票的最佳时机||| 分析:只能买卖两次,就是说有五个状态: 没有买过第一次买入第一次卖出第二次买入第二次卖出 思路:二维数组,记录五个状态 1.dp存储:dp[i][1] 第一次买入 dp[i][2] 第一次卖…...

自定义权限指令与防止连点指令
1.权限指令 // 注册一个全局自定义权限指令 v-permission Vue.directive(permission, {inserted: function(el, binding, vnode) {const {value} binding; // 指令传的值// user:edit:phone,sysData:sampleconst permissions [user:edit:address, sysData:entrust, sysData:…...
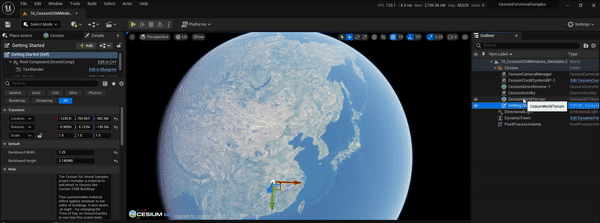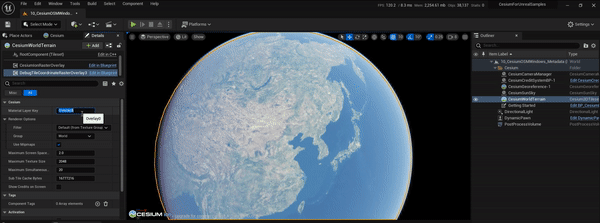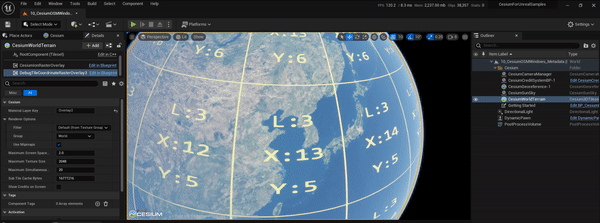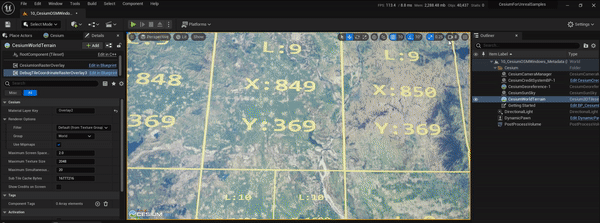
UE5、CesiumForUnreal实现瓦片坐标信息图层效果
文章目录 1.实现目标2.实现过程2.1 原理简介2.2 cesium-native改造2.3 CesiumForUnreal改造2.4 运行测试3.参考资料1.实现目标 参考CesiumJs的TileCoordinatesImageryProvider,在CesiumForUnreal中也实现瓦片坐标信息图层的效果,便于后面在调试地形和影像瓦片的加载调度等过…...

PostgreSQL执行计划
1. EXPLAIN命令 1)PostgreSQL中EXPLAIN命令的语法格式: postgres# \h explain Command: EXPLAIN Description: show the execution plan of a statement Syntax: EXPLAIN [ ( option [, ...] ) ] statement EXPLAIN [ ANALYZE ] [ VERBOSE ] statementwhere option can be…...

【2023 睿思芯科 笔试题】~ 题目及参考答案
文章目录 1. 题目 & 答案单选题编程题问题1:解析1:问题2:解析2: 声明 名称如标题所示,希望大家正确食用(点赞转发评论) 本次笔试题以两种形式考察的,分别是:选择题&a…...

Java手写AVL树
Java手写AVL树 1. AVL树实现思路原理 为了解释AVL树的实现思路原理,下面使用Mermanid代码表示该算法的思维导图: #mermaid-svg-ycH8kKpzVk2HWEby {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid…...

运维自动化:提高效率的秘诀
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
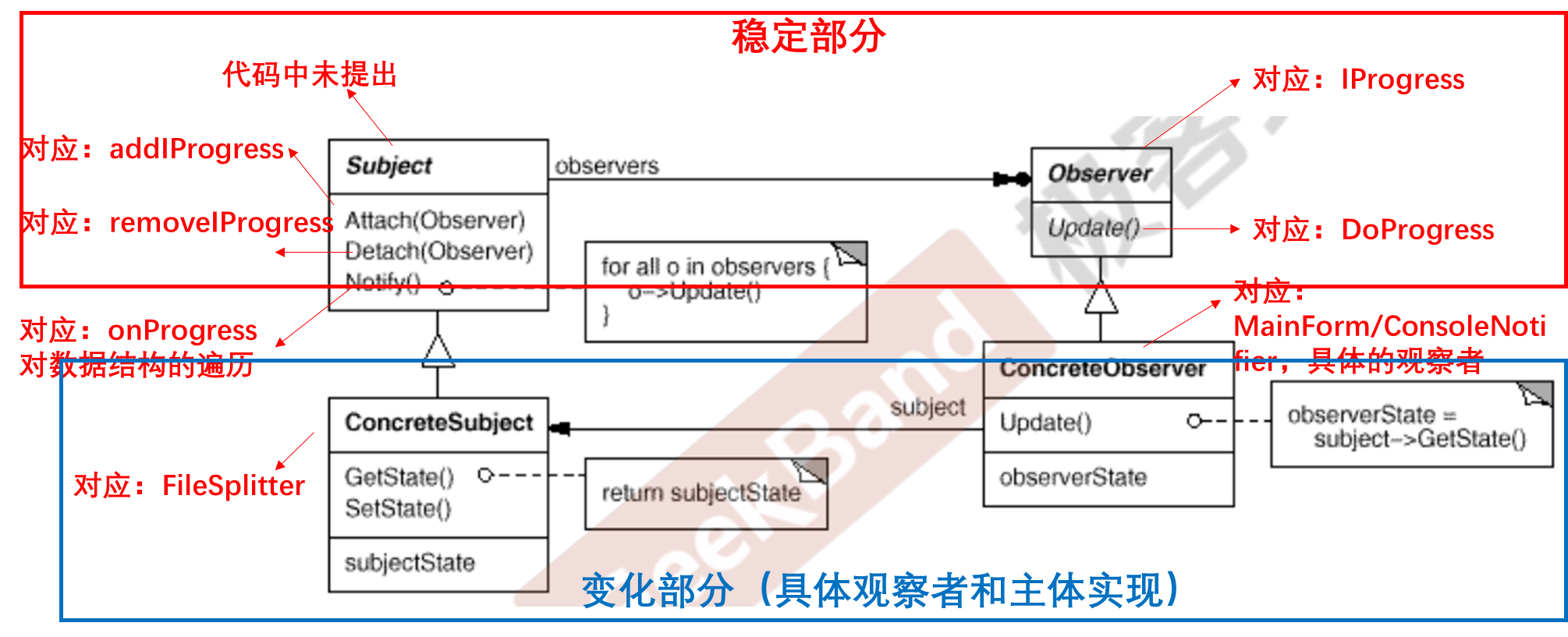
C++设计模式_05_Observer 观察者模式
接上篇,本篇将会介绍C设计模式中的Observer 观察者模式,和前2篇模板方法Template Method及Strategy 策略模式一样,仍属于“组件协作”模式。Observer 在某些领域也叫做 Event 。 文章目录 1. 动机( Motivation)2. 代码…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
