使用redis+lua通过原子减解决超卖问题【示例】
系列文章目录
一、SpringBoot连接MySQL数据库实例【tk.mybatis连接mysql数据库】
二、SpringBoot连接Redis与Redisson【代码】
三、SpringBoot整合WebSocket【代码】
四、使用redis+lua通过原子减解决超卖问题【示例】
五、SpringBoot整合Elasticsearch【代码示例】
文章目录
- 系列文章目录
- 前言
- 一、准备工作
- 二、不使用Lua
- 三、使用Lua
前言
超卖,即在并发的情况下,所售商品数量大于商品的库存数量。在并发量大的情况下,用户请求同时到达,对数据库进行操作,在没有采取相应的处理的情况时从而导致出现超卖现象。
一、准备工作
在redis中放入十件商品

二、不使用Lua
使用20个线程抢商品
public void test () {ExecutorService service = Executors.newFixedThreadPool(20);for (int i = 0; i < 20; i++) {int finalI = i;service.execute(new Runnable() {@Overridepublic void run() {if (Integer.parseInt(String.valueOf(redisUtils.get("test"))) > 0) {int execute = Integer.parseInt(String.valueOf(redisUtils.decr("test", 1)));if (execute != 0) {log.info("线程" + finalI + "抢到了商品!!!");} else {log.info("线程" + finalI + "未抢到商品");}} else {log.info("商品数量不足");}}});}
}
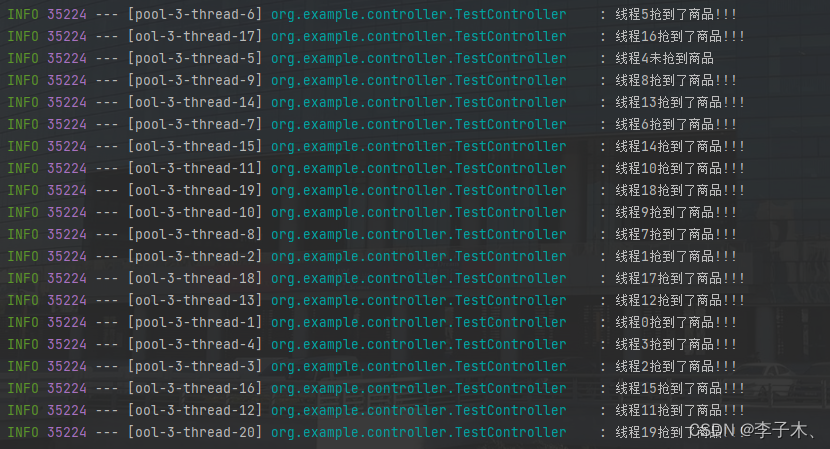
运行代码发现已经超出了十个人抢到了商品。
此时redis的存值已经变为了负数,出现了超卖的情况。

三、使用Lua
public void test_lua () {StringBuilder sb = new StringBuilder();sb.append("if (redis.call('exists', KEYS[1]) == 1) then"); // 判断key是否存在sb.append(" local stock = tonumber(redis.call('get', KEYS[1]));"); // 获取锁sb.append(" if (stock == -1) then");sb.append(" return 1;");sb.append(" end;");sb.append(" if (stock > 0) then");sb.append(" redis.call('decrby', KEYS[1], 1);"); // 商品数量减1sb.append(" return stock;");sb.append(" end;");sb.append(" return 0;");sb.append("end;");sb.append("return -1;");String STOCK_LUA = sb.toString();DefaultRedisScript<Long> objectDefaultRedisScript = new DefaultRedisScript<>();objectDefaultRedisScript.setScriptText(STOCK_LUA);objectDefaultRedisScript.setResultType(Long.class);ArrayList<String> keys = new ArrayList<>(); // 脚本中的KEYS参数keys.add("test");ExecutorService service = Executors.newFixedThreadPool(20);for (int i = 0; i < 20; i++) {int finalI = i;service.execute(new Runnable() {@Overridepublic void run() {int execute = Integer.parseInt(redisTemplate.execute(objectDefaultRedisScript, keys).toString());if (execute != 0) {log.info("线程" + finalI + "抢到了商品!!!");} else {log.info("线程" + finalI + "未抢到商品");}}});}
}
依然使用20个线程抢商品,运行代码只有10个线程抢到了商品
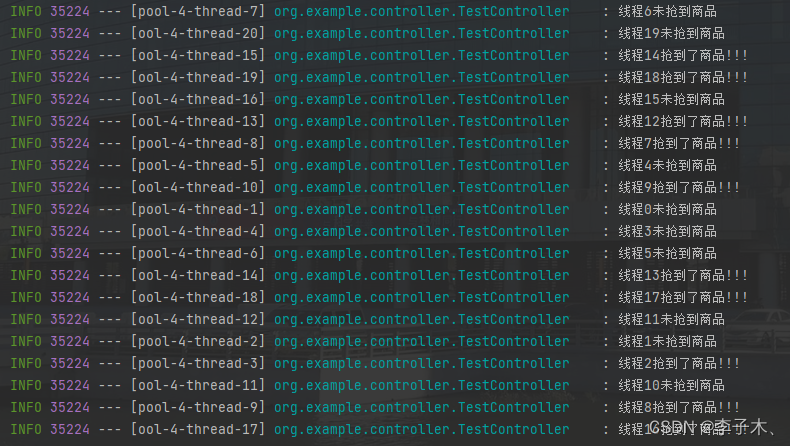
此时redis中的存值为0

相关文章:

使用redis+lua通过原子减解决超卖问题【示例】
系列文章目录 一、SpringBoot连接MySQL数据库实例【tk.mybatis连接mysql数据库】 二、SpringBoot连接Redis与Redisson【代码】 三、SpringBoot整合WebSocket【代码】 四、使用redislua通过原子减解决超卖问题【示例】 五、SpringBoot整合Elasticsearch【代码示例】 文章目录 系…...

WebFlux异常处理:onErrorReturn和onErrorResume
1 缘起 最近在学习WebFlux, 处理异常时遇到些问题,比如,Java直接抛出的异常无法直接被onErrorReturn和onErrorResume捕获, 但是,在map或者flatMap等方法之后的异常又可以直接被捕获, 于是,进行…...

《动手学深度学习 Pytorch版》 4.5 权重衰减
4.5.1 范数与权重衰减 整节理论,详见书本。 4.5.2 高维线性回归 %matplotlib inline import torch from torch import nn from d2l import torch as d2l# 生成一些数据,为了使过拟合效果更明显,将维数增加到 200 并使用一个只包含 20 个样…...

数据脱敏的风险量化评估介绍
1、背景介绍 当前社会信息化高速发展,网络信息共享加速互通,数据呈现出规模大、流传快、类型多以及价值密度低的特点。人们可以很容易地对各类数据实现采集、发布、存储与分析,然而一旦带有敏感信息的数据被攻击者获取将会造成个人隐私的严重…...
)
SpringCloudGateway网关实战(三)
SpringCloudGateway网关实战(三) 上一章节我们讲了gateway的内置过滤器Filter,本章节我们来讲讲全局过滤器。 自带全局过滤器 在实现自定义全局过滤器前, spring-cloud-starter-gateway依赖本身就自带一些全局过滤器࿰…...

08在MyBatis-Plus中配置多数据源
配置多数据源 模拟多库场景 适用于多种场景: 多库(操作的表分布在不同数据库当中),读写分离(有的数据库负责查询的功能,有的数据库负责增删该的功能),一主多从,混合模式等 第一步: 模拟多库,在mybatis_plus数据库中创建user表,在mybatis_plus_1数据库中创建product表 --创建…...
Centos8安装docker并配置Kali Linux图形化界面
鉴于目前网上没有完整的好用的docker安装kali桌面连接的教程,所以我想做一个。 准备工作 麻了,这服务器供应商提供的镜像是真的纯净,纯净到啥都没有。 问题一:Centos8源有问题 Error: Failed to download metadata for repo ap…...
游戏开发初等数学基础
凑数图() 立体图形面积体积 1. 立方体(Cube): 表面积公式: 6 a 2 6a^2 6a2 (其中 a a a 是边长)。体积公式: a 3 a^3 a3 (其中 a a a 是边长)。 2. 球体(Sphere): 表面积公…...

svg图片代码data:image/svg+xml转png图片方法
把代码保存为html格式的文件中,用浏览器访问,即可右键保存 从AI软件或其它网站得到svg图片代码后,把他复制到下面源码上 注意:src""图片地址中,一些参数的含义 d‘这里是图片代码数据’ viewBox是图片显示区域,宽,高等 fill%23000000’这里表示颜色 ,后面6位0表示黑色…...

解决问题:Replace `‘vue‘;⏎` with `“vue“;`
使用vscode写vue文件的问题: Replace vue;⏎ with "vue"; error Replace v-model:value"xxx"placeholder"inputsearch prettier/prettier 7:38 error Insert ⏎ potentially fixable with the --fix option 原因:格式问题&a…...
ThinkPHP 5.0通过composer升级到5.1,超级简单
事情是这样的,我实现一个验证码登录的功能,但是这个验证码的包提示tp5的版本可以是5.1.1、5.1.2、5.1.3。但我使用的是5.0,既然这样,那就升个级呗,百度了一下,结果发现大部分都是讲先备份application和修改…...
计算机竞赛 多目标跟踪算法 实时检测 - opencv 深度学习 机器视觉
文章目录 0 前言2 先上成果3 多目标跟踪的两种方法3.1 方法13.2 方法2 4 Tracking By Detecting的跟踪过程4.1 存在的问题4.2 基于轨迹预测的跟踪方式 5 训练代码6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习多目标跟踪 …...

一文了解大模型工作原理——以ChatGPT为例
文章目录 写在前面1.Tansformer架构模型2.ChatGPT原理3.提示学习与大模型能力的涌现3.1 提示学习3.2 上下文学习3.3 思维链 4.行业参考建议4.1 拥抱变化4.2 定位清晰4.3 合规可控4.4 经验沉淀 写在前面 2022年11月30日,ChatGPT模型问世后,立刻在全球范围…...

CPP-Templates-2nd--第十九章 萃取的实现 19.7---
目录 19.7 其它的萃取技术 19.7.1 If-Then-Else 19.7.2 探测不抛出异常的操作 19.7.3 萃取的便捷性(Traits Convenience) 别名模板和萃取(Alias Templates And Traits) 变量模板和萃取(Variable Templates and Traits&…...
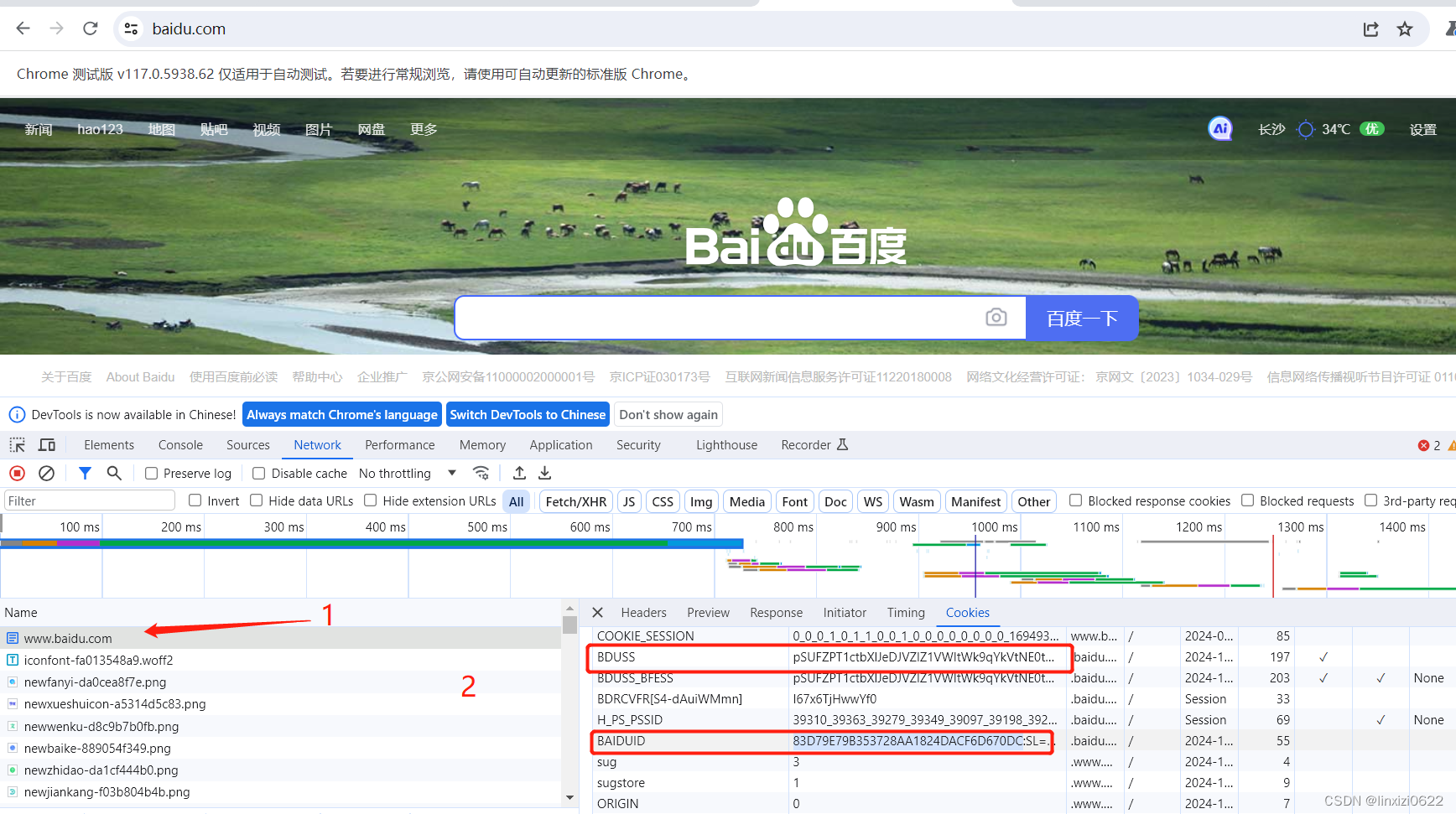
python 采用selenium+cookies 获取登录后的网页
百度网页由于需要登陆手机短信验证。比较麻烦 这里我采用先人工登录百度账号,然后将百度账号的相关cookies保存下来 然后采用selenium动态登录网页 整体代码如下 from selenium import webdriverimport timeoptions webdriver.ChromeOptions()options.add_argu…...

【测试开发】答疑篇 · 什么是软件测试
【测试开发】答疑篇 文章目录 【测试开发】答疑篇1. 生活中的测试2. 什么是软件测试3. 为什么要有测试/没有测试行不行4. 软件测试和软件开发的区别5. 软件测试和软件调试之间的区别6. 软件测试的岗位7. 优秀测试人员具备的素质 【测试开发】答疑篇 软件不一定是桌面应用&#…...
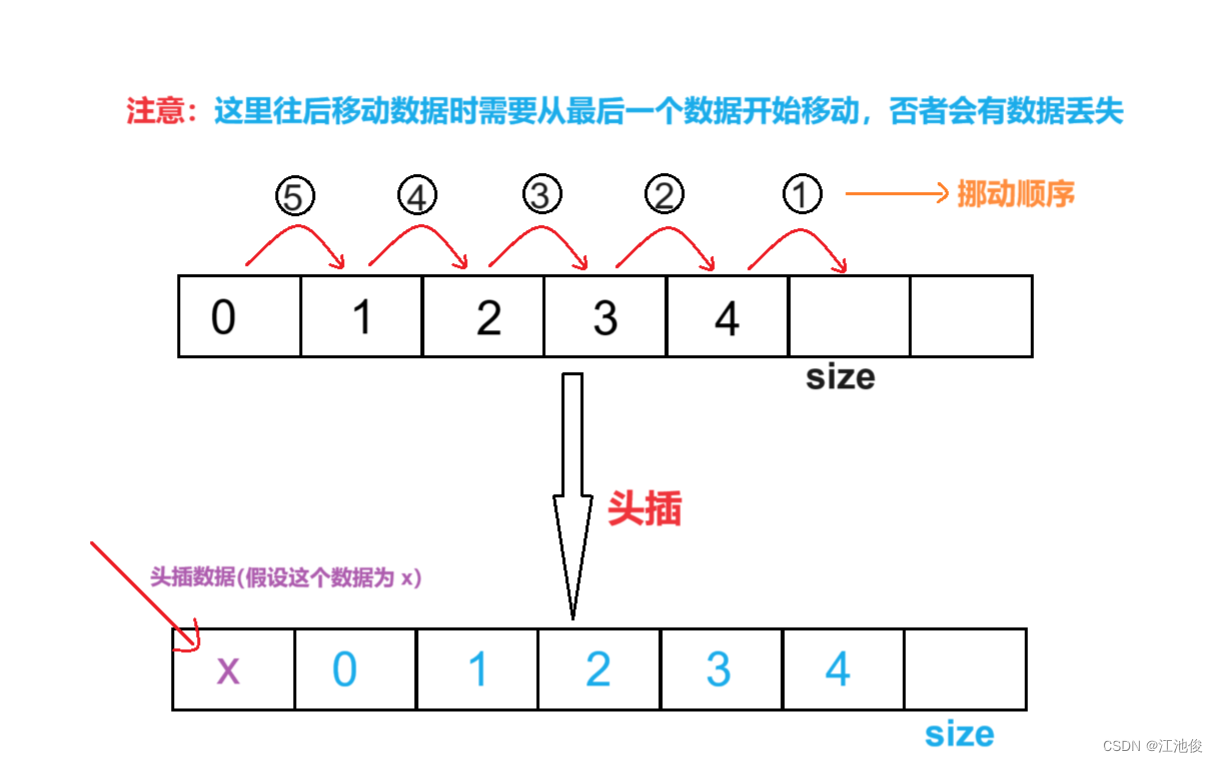
深入解析顺序表:揭开数据结构的奥秘,掌握顺序表的精髓
💓 博客主页:江池俊的博客⏩ 收录专栏:数据结构探索👉专栏推荐:✅C语言初阶之路 ✅C语言进阶之路💻代码仓库:江池俊的代码仓库🔥编译环境:Visual Studio 2022Ἰ…...

数据风险量化评估方案
一、企业面临数据安全的痛点 1、企业缺少清晰的数据安全意识 各部门重视度不够,缺少主动数据安全管控意识。数据安全管控架构不清晰,职责划分不明确。对数据安全管控认识不全面、不深刻。工作人员对于所持有的数据缺乏概念,导致数据的价值无…...

EasyAVFilter代码示例之将视频点播文件转码成HLS(m3u8+ts)视频点播格式
以下是一套完整的视频点播功能开发源码,就简简单单几行代码,就可以完成原来ffmpeg很复杂的视频点播转码调用流程,而且还可以集成在自己的应用程序中调用,例如java、php、cgo、c、nodejs,不需要再单独一个ffmpeg的进程来…...
动态规划 part 11)
day-50 代码随想录算法训练营(19)动态规划 part 11
123.买卖股票的最佳时机||| 分析:只能买卖两次,就是说有五个状态: 没有买过第一次买入第一次卖出第二次买入第二次卖出 思路:二维数组,记录五个状态 1.dp存储:dp[i][1] 第一次买入 dp[i][2] 第一次卖…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
