DM@数理逻辑@命题公式及其赋值@真值表@公式分类
文章目录
- abstract
- 命题公式及其赋值
- 命题常项
- 命题变项
- 命题公式
- 合式公式(命题公式)
- 限定基本联结词的合适公式的定义
- 合式公式中的0和1
- 子公式
- **公式的层次定义**
- 分层加括号
- 命题公式的赋值和解释
- 成真赋值@成假赋值
- 公式的书写规范@括号的省略
- 真值表
- 赋值方法数量
- 构造真值表
- 公式分类
abstract
DM@数理逻辑@命题公式及其赋值@真值表@公式分类
命题公式及其赋值
命题常项
- 简单命题是命题逻辑中最基本的研究单位,其真值式确定的,称为命题常项或命题常元
- 命题常项相当于初等数学中的常数(0,1)
命题变项
- 对应于初等数学中的变量,命题逻辑中有:取值1(真)或0(假)的变元称为命题变项或命题变元
- 用命题变项表示真值可以变换的陈述句
- 命题变项不是命题,其和命题常项的关系如同初等数学中变量与常量的关系
命题公式
合式公式(命题公式)
- 将命题变相用联结词和圆括号按一定逻辑关系联系起来的符号串,称为合式公式
- 单个命题变项是合式公式,且称为原子命题公式
限定基本联结词的合适公式的定义
- 当使用联结词集{ ¬ , ∨ , ∧ , → , ↔ \neg,\vee,\wedge,\to,\leftrightarrow ¬,∨,∧,→,↔}时,合式公式定义(递归定义)为:
- 单个命题变项是合式公式
- 若 A , B A,B A,B都是合式公式,则 ( ¬ A ) (\neg{A}) (¬A), ( A ∨ B ) (A\vee{B}) (A∨B), ( A ∧ B ) (A\wedge{B}) (A∧B), ( A → B ) , ( A ↔ B ) (A\to{B}),(A\leftrightarrow{B}) (A→B),(A↔B)是合式公式.不妨称这几个公式为一层公式
- 有限次应用(2)中的方式形成的符号串是合式公式
- 合式公式也成为命题公式,简称公式
- Note:
- 析取联结词 ∧ \wedge ∧不能省略不写
- 任意两个不重叠的子公式都要有二元联结词( T T T中的联结词)链接,例如 p q → r pq\to{r} pq→r就不是合式公式,而 p ∧ q → r p\wedge{q}\to{r} p∧q→r是合式公式
合式公式中的0和1
- 合适公式可以出现0,1它们分别视为 p ∧ ¬ p p\wedge{\neg{p}} p∧¬p, p ∨ ¬ p p\vee{\neg{p}} p∨¬p;两种表示可以相互替换和解释
子公式
- 设 A A A为合式公式, B B B是 A A A中的一部分(子串),则称 B B B是 A A A的子公式
公式的层次定义
-
若公式 A A A是单个命题变项,则 A A A称为0层公式
-
设 B B B是 n n n层公式,则 A = ¬ B A=\neg{B} A=¬B是 n + 1 n+1 n+1层公式
-
称设 B , C B,C B,C分别是 i , j i,j i,j层公式,且 n = max ( i , j ) n=\max(i,j) n=max(i,j),则 A = B ∗ C A=B*{C} A=B∗C是 n + 1 n+1 n+1层的( ∗ ∈ T = { ∨ , ∧ , → , ↔ } *\in T=\{\vee,\wedge,\to,\leftrightarrow\} ∗∈T={∨,∧,→,↔})
- 即, A = B ∧ C A=B\wedge{C} A=B∧C, A = B ∨ C A=B\vee{C} A=B∨C, A = B → C A=B\to{C} A=B→C, A = B ↔ C A=B\leftrightarrow{C} A=B↔C的层数是 1 + max ( i , j ) 1+\max{(i,j)} 1+max(i,j)
分层加括号
- 例如: ( ¬ p ∨ q ) → r (\neg{p}\vee{q})\to{r} (¬p∨q)→r可以通过加括号处理,(对1层及上的子公式加括号)使得计数其层数更加容易: ( ( ( ¬ p ) ∨ q ) → r ) (((\neg{p})\vee{q})\to{r}) (((¬p)∨q)→r),可以看到,该公式的最深称括号有3层,各层如下
- 0层: p , q , r p,q,r p,q,r,(我们通常对0层不感兴趣)
- 1层: ¬ p \neg{p} ¬p,
- 2层: ¬ p ∨ q \neg{p}\vee{q} ¬p∨q
- 3层: ( ¬ p ∨ q ) → r (\neg{p}\vee{q})\to{r} (¬p∨q)→r
- 例: ( ¬ ( p → ¬ q ) ) ∧ ( ( r ∨ s ) ↔ ¬ p ) (\neg{(p\to{\neg{q}})}) \wedge{((r\vee{s)\leftrightarrow{\neg{p}}})} (¬(p→¬q))∧((r∨s)↔¬p),可以加括号为: ( ( ¬ ( p → ( ¬ q ) ) ) ∧ ( ( r ∨ s ) ↔ ( ¬ p ) ) ) ((\neg{(p\to{(\neg{q})})}) \wedge{((r\vee{s)\leftrightarrow{(\neg{p})}})}) ((¬(p→(¬q)))∧((r∨s)↔(¬p)));可见其有4层
命题公式的赋值和解释
-
设 p 1 , ⋯ , p n p_1,\cdots,p_n p1,⋯,pn是出现在公式 A A A中的全部命题变项(公式 A A A表示为 A ( p 1 , ⋯ , p n ) A(p_1,\cdots,p_n) A(p1,⋯,pn)),分别为这 n n n个命题变项指定一个真值,称为对公式 A A A的一个赋值或解释
-
写法: p 1 = α 1 , ⋯ , p n = α n p_1=\alpha_1,\cdots,p_n=\alpha_n p1=α1,⋯,pn=αn可以简写为 α 1 , ⋯ , α n \alpha_1,\cdots,\alpha_n α1,⋯,αn
成真赋值@成假赋值
- 若指定一组值使得 A A A为1,记为 A = 1 A=1 A=1,称这组值为 A A A的成真赋值
- 若 A = 0 A=0 A=0,则称这组值为 A A A的成假赋值
公式的书写规范@括号的省略
- 为了方便起见,一层公式单独出现的时候,可以省略括号不写,
- 公式中不影响运算次序的括号也可以省去,例如 ( p ∨ q ) ∨ ( ¬ r ) (p\vee{q})\vee{(\neg{r})} (p∨q)∨(¬r)可以简写为 p ∨ q ∨ ¬ r p\vee{q}\vee\neg{r} p∨q∨¬r
真值表
- 反映公式 A A A所有取值及其结果的表称为 A A A的真值表
赋值方法数量
- n n n个命题变项(构成)的公式有 2 n 2^{n} 2n种不同的赋值方法
- 将 n n n个命题变项(构成)的公式全体构成的集合记为 F ( n ) F(n) F(n),意味着 F ( n ) F(n) F(n)中公式的真值表有 2 n 2^{n} 2n行
构造真值表
总体步骤是,列出 2 n 2^{n} 2n个不同的赋值,分别计算它们的真值,具体的操作如下:
- 找出公式中所有的命题变项 p 1 , ⋯ , p n p_1,\cdots,p_n p1,⋯,pn,列出 2 n 2^{n} 2n个赋值
- 赋值从 0 ⋯ 0 0\cdots0 0⋯0,按二进制加法加1生成下一个赋值,到 1 ⋯ 1 1\cdots1 1⋯1为止,恰好 2 n 2^{n} 2n个赋值
- 公式层次分析:从低层次到高层的顺序分解公式的各个层次
- 对应各个赋值计算各个层次的真值,那么最后一个层次的真值就是整个公式的真值
例: ( ¬ p ∧ q ) → ¬ r (\neg{p}\wedge{q})\to{\neg{r}} (¬p∧q)→¬r
| p q r pqr pqr | ¬ p \neg{p} ¬p | ¬ r \neg{r} ¬r | ¬ p ∧ q \neg{p}\wedge{q} ¬p∧q | ( ¬ p ∧ q ) → ¬ r (\neg{p}\wedge{q})\to{\neg{r}} (¬p∧q)→¬r |
|---|---|---|---|---|
| 000 | 1 | 1 | 0 | 1 |
| 001 | 1 | 0 | 0 | 1 |
| 010 | 1 | 1 | 1 | 1 |
| 011 | 1 | 0 | 1 | 0 |
| 100 | 0 | 0 | 0 | 1 |
| 101 | 0 | 0 | 0 | 1 |
| 110 | 0 | 1 | 0 | 1 |
| 111 | 0 | 0 | 0 | 1 |
- 第1列是赋值,第2,3列是第一层子式,第3列示第3层子式,最后一列是整个公式的真值
- 其中非首尾的各列是为了提高计算正确率的辅助列,并不是一个真值表必须的列
- 第一列也可以看作是0层列,低层的列可以帮助计算高层的列,减少重复计算
公式分类
- 若 A A A在所有赋值下取值均为真,则 A A A称为重言式或永真式( A A A的真值表最后一列全为1)
- 若 A A A在它的所有赋值下取值均为假,则 A A A称为矛盾式或永假式( A A A的真值表最后一列全为0)
- 若 A A A不是矛盾式,则 A A A使可满足式,特别的,若至少存在一个成假赋值,则称 A A A为非重言可满足式
相关文章:

DM@数理逻辑@命题公式及其赋值@真值表@公式分类
文章目录 abstract命题公式及其赋值命题常项命题变项 命题公式合式公式(命题公式)限定基本联结词的合适公式的定义合式公式中的0和1子公式 **公式的层次定义**分层加括号 命题公式的赋值和解释成真赋值成假赋值公式的书写规范括号的省略 真值表赋值方法数量构造真值表 公式分类…...

HTTP协议(超级详细)
HTTP协议介绍 基本介绍: HTTP:超文本传输协议,是从万维网服务器传输超文本到本地浏览器的传送协议HTTP是一种应用层协议,是基于TCP/IP通信协议来传送数据的,其中 HTTP1.0、HTTP1.1、HTTP2.0 均为 TCP 实现࿰…...

leetcode做题笔记135. 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。 你需要按照以下要求,给这些孩子分发糖果: 每个孩子至少分配到 1 个糖果。相邻两个孩子评分更高的孩子会获得更多的糖果。 请你给每个孩子分发糖果,计算并返回需要准备的…...
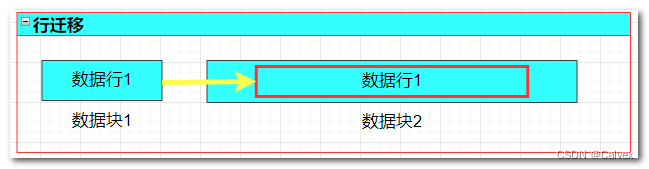
Oracle数据库体系结构(三)_逻辑结构
Oracle逻辑存储结构,主要描述oracle 数据库内部数据的组织和管理方式,即在数据库管理系统的层面中如何组织和管理数据,与操作系统没有关系。逻辑存储结构时候物理存储机构的抽象体现,是不可见的,可以通过查询数据库数据字典了解逻…...

在 Python 中计算两个 GPS 点之间的距离
计算两个 GPS 点之间的距离是我们可以在 Python 框架内操作的地理和数学练习。 现在让我们看看如何使用 Python 执行此操作。 在 Python 中使用 Haversine 公式计算两个 GPS 点之间的距离 haversine 公式是用 Python 计算两个 GPS 点之间距离的一种简化方法,但它的计算是基于…...
影刀RPA解决WPS不存在的问题
问题阐述 明明电脑上已经安装了WPS,但影刀程序还是提示没有安装的问题 解决办法 1.打开WPS并关闭所有其他网页 2. 配置与修复 3.开始修复 出现这个框,就要关闭WPS,否则无法执行,关闭WPS不影响其修复 4.等待修复完成即可...

vue动态路由切换刷新保留历史路由搜索条件数据
最近有客户反映我们系统按条件查询完列表进入详情页后再返回列表页时页面没有展示他查询的那条数据,而是进入页面一贯会展示按无条件查询的数据,希望我们能对列表做查询缓存,那咱们就用keep-alive来实现一下 AppMain.vue include 属性绑定一个…...

免费:CAD批量转PDF工具,附下载地址
分享一款CAD 批量转PDF、打印的工具插件。能自动识别图框大小、自动识别比例、自动编号命名。重点!重点!重点!自动将CAD的多张图纸一次性地、批量地转为PDF,或者打印。效果看下图: 适用环境: 32位系统 Auto…...

无涯教程-JavaScript - FACT函数
描述 The FACT function returns the factorial of a number. The factorial of a number is equal to 1*2*3*...* number. 语法 FACT (number)争论 Argument描述Required/OptionalNumberThe nonnegative number for which you want the f…...

UART 协议
文章目录 电气层硬件拓扑基本原理协议空闲位起始位数据位奇偶校验位无校验奇校验偶校验mark parityparity 停止位 波特率优缺点优点缺点 参考 UART(universal asynchronous receiver-transmitter) 通用异步收发器 分类特点导线2速度9600, 19200, 38400&…...
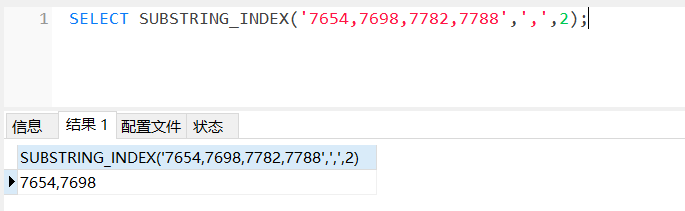
MySql中分割字符串
MySql中分割字符串 在MySql中分割字符串可以用到SUBSTRING_INDEX(str, delim, count) 参数解说 解释 str 需要拆分的字符串 delim 分隔符,通过某字符进行拆分 count 当 count 为正数&…...

Ubuntu 22.04安装过程
iso下载地址 Ubuntu Releases 1.进入引导菜单 选择Try or Install Ubuntu Server安装 2.选择安装语言 默认选择English 3.选择键盘布局 默认即可 4.选择安装服务器版本 最小化安装 5.配置网络 选择ipv4 选择自定义 DHCP也可 6.配置代理 有需要可以配置 这里跳过 7.软件源 …...

【算法|虚拟头节点|链表】移除链表元素
Leetcode203 移除链表元素 题目描述: 给你一个链表的头节点 head 和一个整数 val ,请你删除链表中所有满足 Node.val val 的节点,并返回 新的头节点 。 示例 1: 输入:head [1,2,6,3,4,5,6], val 6 输出…...
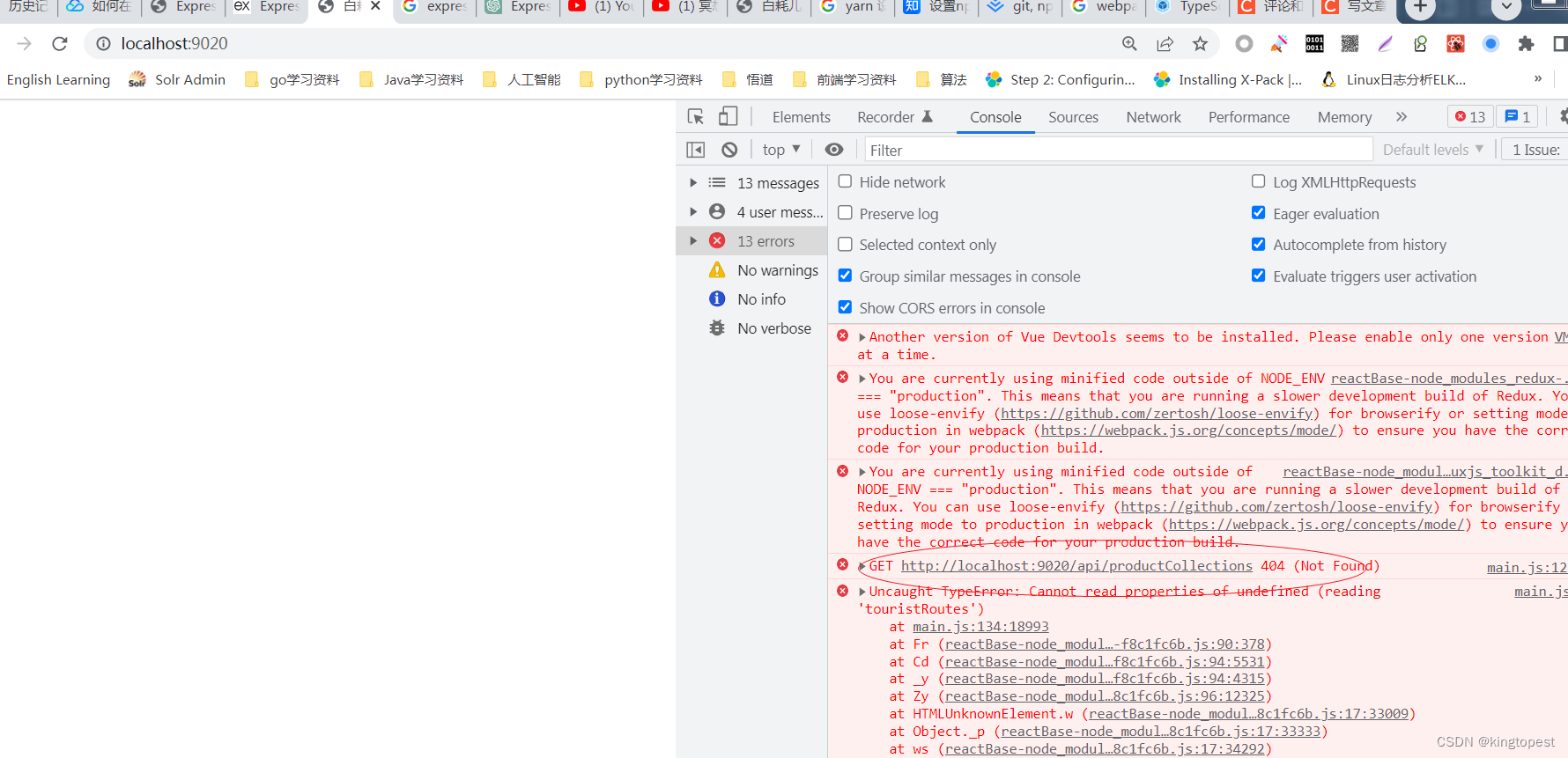
express静态路由匹配引发的404错误
最近有一个react项目,我用webpack打包,然后使用express作为webserver跑起来。 但是在运行的时候,就白屏了,看console原来是报了404错误 可是代码里面明明有路由定义,为什么还是报404错误呢? app.get("…...
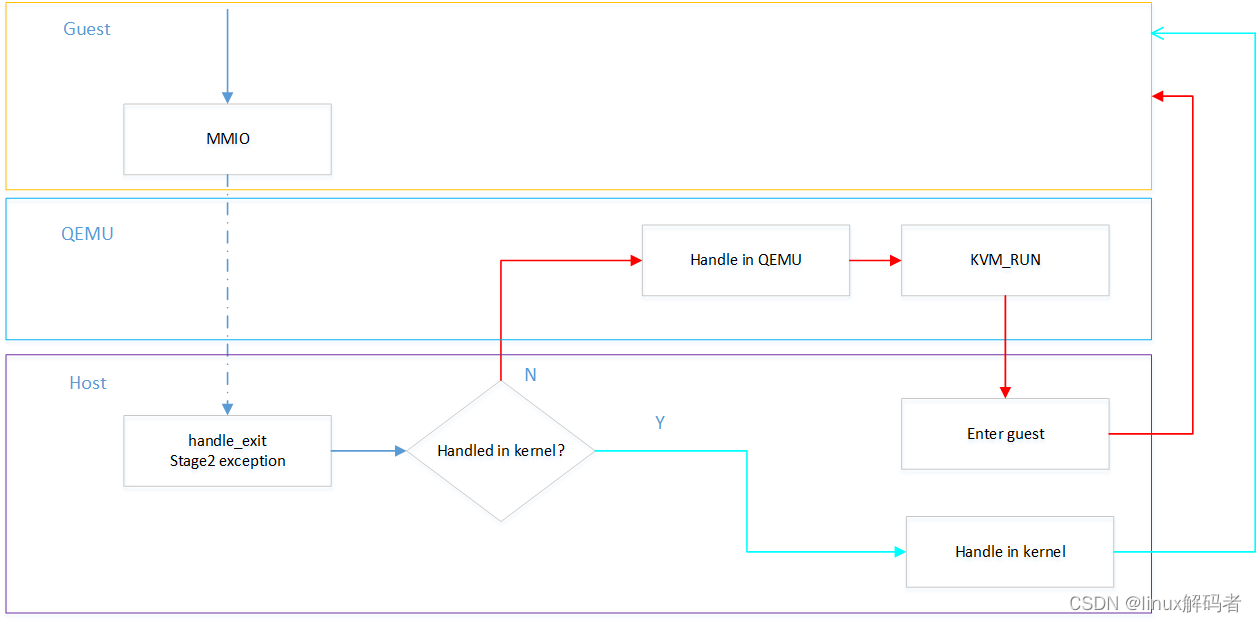
VHOST-SCSI代码分析(4)VHOST KICK机制
在VIRTIO框架中虚拟机通知QEMU数据准备好是通过操作MMIO,在KVM中将操作分发到QEMU中,由QEMU中模拟对应的MMIO操作(图中红色部分)。 VHOST框架虚拟机通知HOST内核数据准备好也是通过MMIO操作,但在函数vhost_dev_enable_…...
)
Docker Volume(存储卷)
文章目录 Docker Volume(存储卷)1.什么是存储卷?2.为什么需要存储卷?3. 存储卷的分类1) 管理卷Volume方式一:Volume命令操作方式二: -v 或者--mount 指定方式三: Dockerfile 匿名卷小结Docker 卷生命周期Docker 卷共享…...
【毕设选题】opencv 图像识别 指纹识别 - python
文章目录 0 前言1 课题背景2 效果展示3 具体实现3.1 图像对比过滤3.2 图像二值化3.3 图像侵蚀细化3.4 图像增强3.5 特征点检测 4 OpenCV5 最后 0 前言 🔥 这两年开始毕业设计和毕业答辩的要求和难度不断提升,传统的毕设题目缺少创新和亮点,往…...

阿里云无影云电脑使用初体验:真的好用吗?
阿里云无影云电脑即无影云桌面,云桌面如何使用?云桌面购买后没有用户名和密码,先创建用户设置密码,才可以登录连接到云桌面。云桌面想要访问公网还需要开通互联网访问功能。阿里云百科来详细说下阿里云无影云电脑从购买、创建用户…...

无涯教程-JavaScript - FLOOR.MATH函数
描述 FLOOR.MATH函数将数字四舍五入到最接近的整数或最接近的有效倍数。 语法 FLOOR.MATH (number, significance, mode)争论 Argument描述Required/OptionalNumberThe number to be rounded down.RequiredSignificanceThe multiple to which you want to round.OptionalMo…...

Dubbo3基础使用
1、Dubbo概述 现在SpringCloud Alibaba比较火,用的比较多是吧,那dubbo是不是过时的呢? 并不是的,以前有人把Dubbo和SpringCloud进行对比,其实两者是不同维度的,不能对比,dubbo就是一个rpc框架&…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

AxureRP-Pro-Beta-Setup_114413.exe (6.0.0.2887)
Name:3ddown Serial:FiCGEezgdGoYILo8U/2MFyCWj0jZoJc/sziRRj2/ENvtEq7w1RH97k5MWctqVHA 注册用户名:Axure 序列号:8t3Yk/zu4cX601/seX6wBZgYRVj/lkC2PICCdO4sFKCCLx8mcCnccoylVb40lP...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...
