已知平面内三点,求其平面的法向量
三点平面法向量
设三点坐标为A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3)
向量AB=(x2-x1,y2-y1,z2-z1),AC=(x3-x1,y3-y1,z3-z1)
AB、AC所在平面的法向量即AB×AC=(a,b,c),其中:
a=(y2-y1)(z3-z1)-(z2-z1)(y3-y1)
b=(z2-z1)(x3-x1)-(z3-z1)(x2-x1)
c=(x2-x1)(y3-y1)-(x3-x1)(y2-y1)
设 a=(ax,ay,az), b=(bx,by,bz)。i,j,k分别是X,Y,Z轴方向的单位向量,则:
a×b=(aybz-azby)i+(azbx-axbz)j+(axby-aybx)k
a·b=(axbx+ayby+az*bz)
Python代码
def normal_vector(p1, p2, p3):x1, y1, z1 = p1x2, y2, z2 = p2x3, y3, z3 = p3a = (y2 - y1) * (z3 - z1) - (z2 - z1) * (y3 - y1)b = (z2 - z1) * (x3 - x1) - (x2 - x1) * (z3 - z1)c = (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1)return (a, b, c)if __name__ == '__main__':p1 = 1.0, 5.2, 0.0p2 = 2.8, 3.9, 1.0p3 = 7.6, 8.4, 2.0p4 = normal_vector(p1, p2, p3)print(p4)# output (-5.800000000000001, 3.0, 14.340000000000002)
C++代码
#include<iostream>using namespace std;//三维double矢量
struct Vec3d
{double x, y, z;Vec3d(){x = 0.0;y = 0.0;z = 0.0;}Vec3d(double dx, double dy, double dz){x = dx;y = dy;z = dz;}void Set(double dx, double dy, double dz){x = dx;y = dy;z = dz;}
};//计算三点成面的法向量
void Cal_Normal_3D(const Vec3d& v1, const Vec3d& v2, const Vec3d& v3, Vec3d &vn)
{//v1(n1,n2,n3);//平面方程: na * (x – n1) + nb * (y – n2) + nc * (z – n3) = 0 ;double na = (v2.y - v1.y)*(v3.z - v1.z) - (v2.z - v1.z)*(v3.y - v1.y);double nb = (v2.z - v1.z)*(v3.x - v1.x) - (v2.x - v1.x)*(v3.z - v1.z);double nc = (v2.x - v1.x)*(v3.y - v1.y) - (v2.y - v1.y)*(v3.x - v1.x);//平面法向量vn.Set(na, nb, nc);
}int main()
{ // Vec3d v1(1.0, 5.2, 3.7);// Vec3d v2(2.8, 3.9, 4.5);// Vec3d v3(7.6, 8.4, 6.2); // 法向量为:-5.81 0.78 14.34;Vec3d v1(1.0, 5.2, 0.0);Vec3d v2(2.8, 3.9, 1.0);Vec3d v3(7.6, 8.4, 2.0);// 法向量为:-5.8 3 14.34Vec3d vn;Cal_Normal_3D(v1, v2, v3, vn);// cout <<"法向量为:"<< vn.x << '\t' << vn.y << '\t' << vn.z << '\n';cout <<"法向量为:"<< vn.x << " " << vn.y << " " << vn.z << '\n';return 0;
}
相关文章:

已知平面内三点,求其平面的法向量
三点平面法向量 设三点坐标为A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3) 向量AB(x2-x1,y2-y1,z2-z1),AC(x3-x1,y3-y1,z3-z1) AB、AC所在平面的法向量即ABAC(a,b,c),其中: a(y2-y1)(z3-z1)-(z2-z1)(y3-y1) b(z2-z1)(x3-x1)-(z3-z1)(x2-x1) c(x2-x1)(y3-y1)-(x3-x1)(y2-y1)…...

HTML
HTML 1.HTML结构 1.1认识HTML HTML是超文本标记语言,电脑上看到的所有网站都是html实现的 HTML代码是“标签”构成的,简单来说,html就是一堆标签的组合 形如 <body>hello</body>标签名 (body) 放到 < > 中 大部分标签成…...
和最大子数组和算法(如Kadane算法)应用拓展案例)
Java手写最大子数组和算法(如Kadane算法)和最大子数组和算法(如Kadane算法)应用拓展案例
Java手写最大子数组和算法(如Kadane算法)和最大子数组和算法(如Kadane算法)应用拓展案例 1. 算法思维导图 以下是使用mermaid代码表示的Kadane算法的实现原理: #mermaid-svg-rI7hVAVsP1qtjZK7 {font-family:"tr…...

掌握NVM、NRM和NPM:Node.js开发的利器
**掌握NVM、NRM和NPM:Node.js开发的利器** 背景介绍:如何使用NVM:在Windows上安装NVM:在macOS上安装NVM:配置NVM:常用NVM命令: 如何使用NRM:安装NRM:配置全局NRM…...

Nacos 2.2.3 部署到linux
到https://github.com/alibaba/nacos/releases 下载编译后压缩包,如nacos-server-2.2.3.tar.gz这种,里面包含有nacos的jar包,不然启动不了 1.新建并初始化数据库 创建nacos数据库,执行mysql-schema.sql文件,这个文件…...
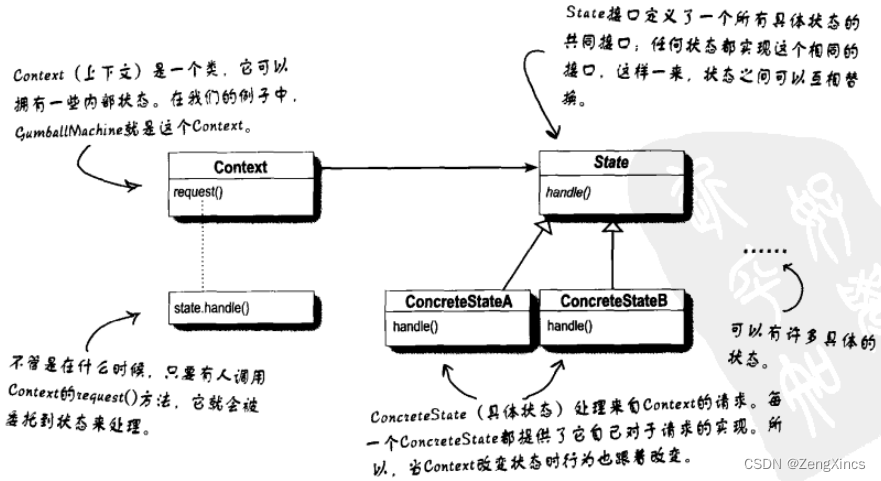
设计模式之十:状态模式
状态模式通过改变对象内部的状态来帮助对象控制自己的行为。 这是一张状态图,其中每个圆圈都是一个状态。 最简单,第一反应的实现就是使用一个变量来控制状态值,并在方法内书写条件代码来处理不同情况。 package headfirst.designpatterns.…...
基本使用指南)
Python 的运算符和语句(条件、循环、异常)基本使用指南
运算符的分类 算数运算符赋值运算符复合赋值运算符比较运算符逻辑运算符 算数运算符 运算符描述实例加1 1 输出结果为 2-减1 - 1 输出结果为 0*乘2 * 2 输出结果为 4/除10 / 2 输出结果为 5//整除9 // 4 输出结果为 2%取余9 % 4 输出结果为 1**指数2 ** 4 输出结果为 16&…...

文心一言 VS 讯飞星火 VS chatgpt (94)-- 算法导论9.2 3题
三、用go语言,给出 RANDOMIZED-SELECT的一个基于循环的版本。 文心一言: 在循环中实现 RANDOMIZED-SELECT 的一个版本可以如下所示。这个版本使用 Go 语言编写,利用随机化来选择一个元素,并在循环中不断地调整选择的元素&#x…...
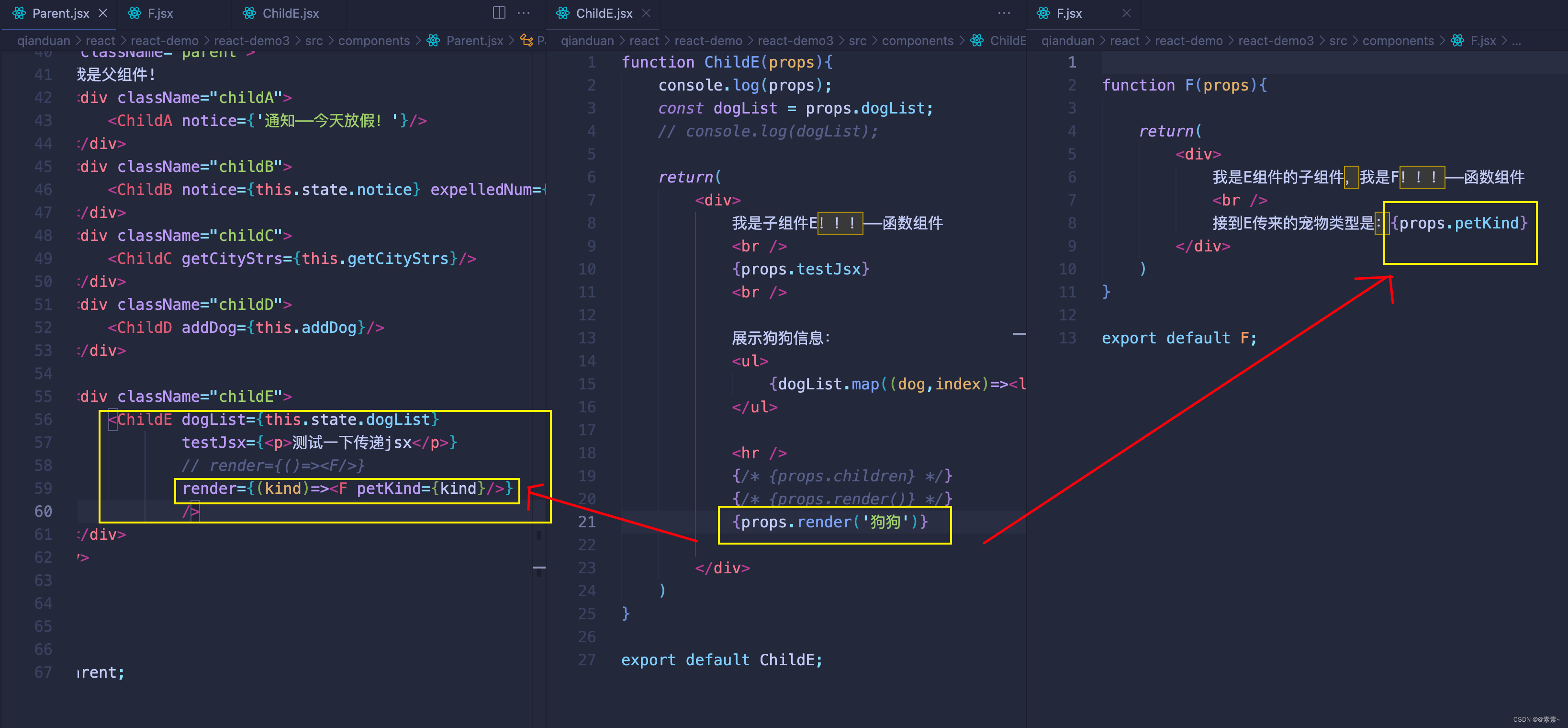
React中组件通信01——props
React中组件通信01——props 1. 父传子——props1.1 简单例子——props1.2 props 可以传递任何数据1.2.1 传递数字、对象等1.2.2 传递函数1.2.3 传递模版jsx 2. 子传父 子传子——props2.1 父传子——传递函数2.2 子传父——通过父传子的函数实现2.3 优化 子传子(…...
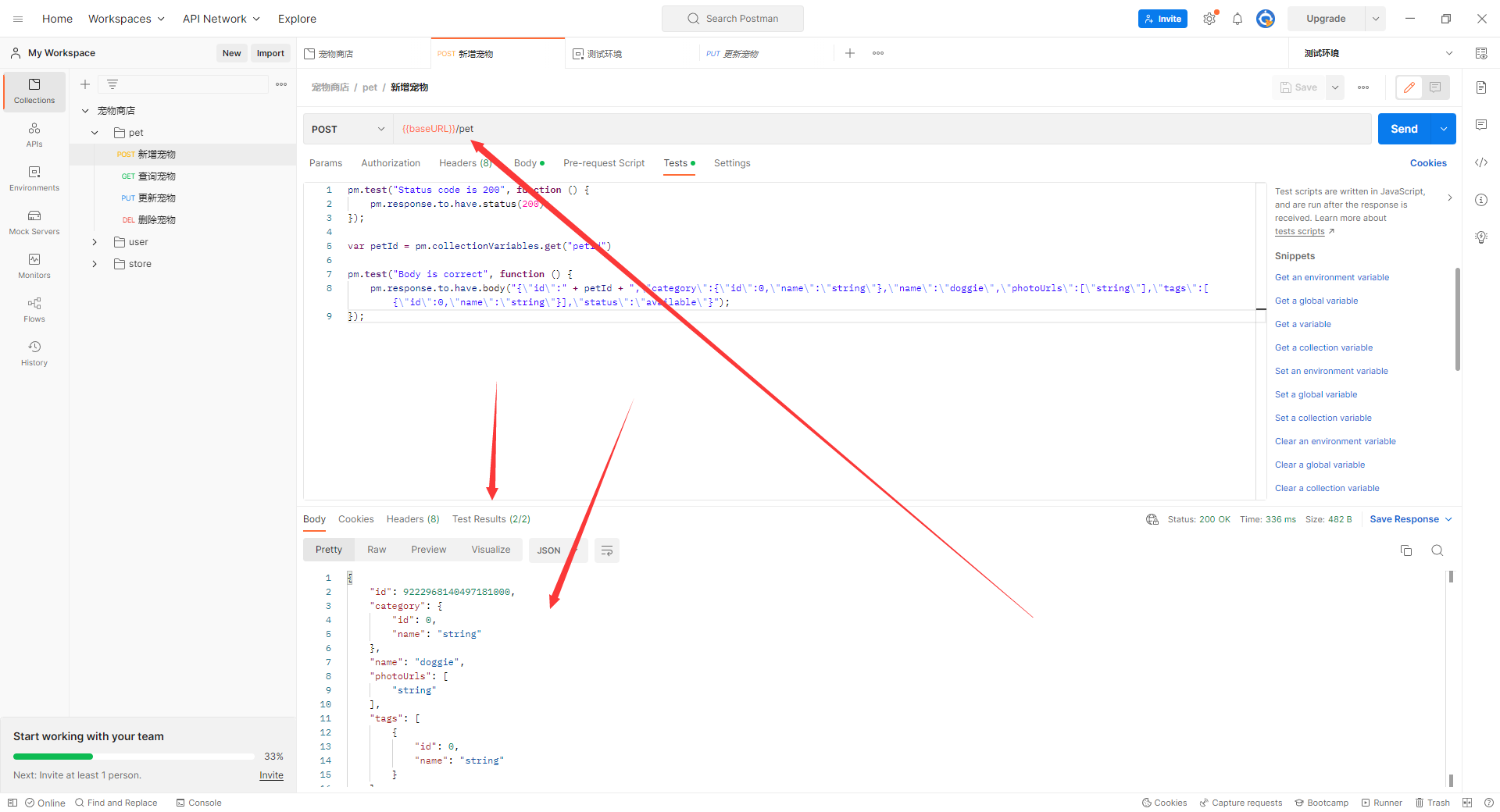
接口测试——接口协议抓包分析与mock_L1
目录: 接口测试价值与体系常见的接口协议接口测试用例设计postman基础使用postman实战练习 1.接口测试价值与体系 接口测试概念 接口:不同的系统之间相互连接的部分,是一个传递数据的通道接口测试:检查数据的交换、传递和控制…...
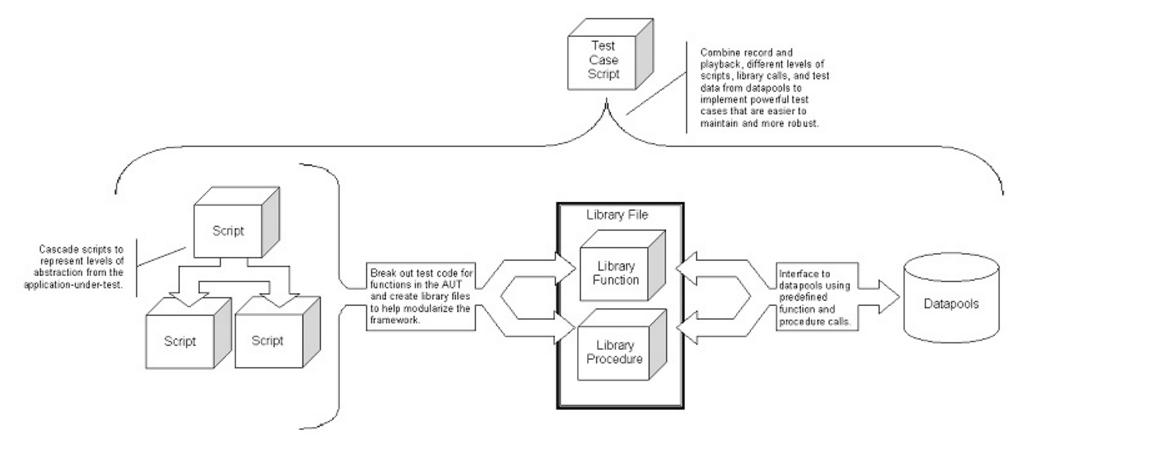
四种常用的自动化测试框架
一直想仔细研究框架,写个流水账似的测试程序不难,写个低维护成本的测试框架就很难了,所以研究多种测试框架还是很有必要的,知道孰优孰劣,才能在开始编写框架的时候打好基础,今天读到了KiKi Zhao的翻译文章&…...
Fuxploider:一款针对文件上传漏洞的安全检测与研究工具
Fuxploider:一款针对文件上传漏洞的安全检测与研究工具 1.概述2. 工具使用1.概述 Fuxploider是一款功能强大的开源渗透测试工具,该工具专门针对文件上传漏洞而设计,可以帮助广大研究人员以自动化的方式检测和利用目标站点文件上传表单中的安全问题 由于该工具基于Python 3…...

Unity 安装及运行MLAgents
1、下载ML-Agents 下载地址 GitHub - Unity-Technologies/ml-agents: The Unity Machine Learning Agents Toolkit (ML-Agents) is an open-source project that enables games and simulations to serve as environments for training intelligent agents using deep reinfo…...

LightDB-A 兼容oracle支持mod操作符
LightDB-A 兼容oracle支持mod操作符 LightDB-A 为了兼容oracle,从23.3版本开始支持mod操作符,其语义同 ‘%’ 操作符,使用案例如下: select 5 mod 2;?column? ----------1 (1 row)select 0 % 0; ERROR: division by zerosel…...

SpringMVC之自定义注解
目录 一、Java注解 1.1 注解简介 1.2 注解分类 1.3 JDK基本注解 1.4 JDK元注解 1.5 自定义注解 1.5.1 标记注解 1.5.2 元数据注解 1.6 如何自定义注解 二、自定义注解的基本案例 2.1 案例一(获取类、方法以及属性上的注解) 2.1.1 Ingerited的…...
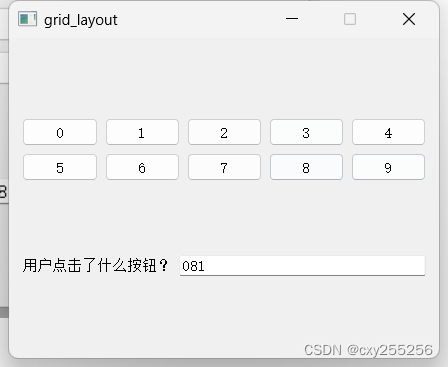
QT:使用普通按钮、网格布局管理器、标签、行编辑器、水平布局管理器、垂直布局管理器做一个小项目
widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPushButton> //普通按钮 #include <QGridLayout> //网格布局管理器 #include <QLabel> //标签 #include <QLineEdit> //行编辑器 #include <QHBoxLayo…...
【小沐学写作】程序员必备技能:在线协作文档汇总
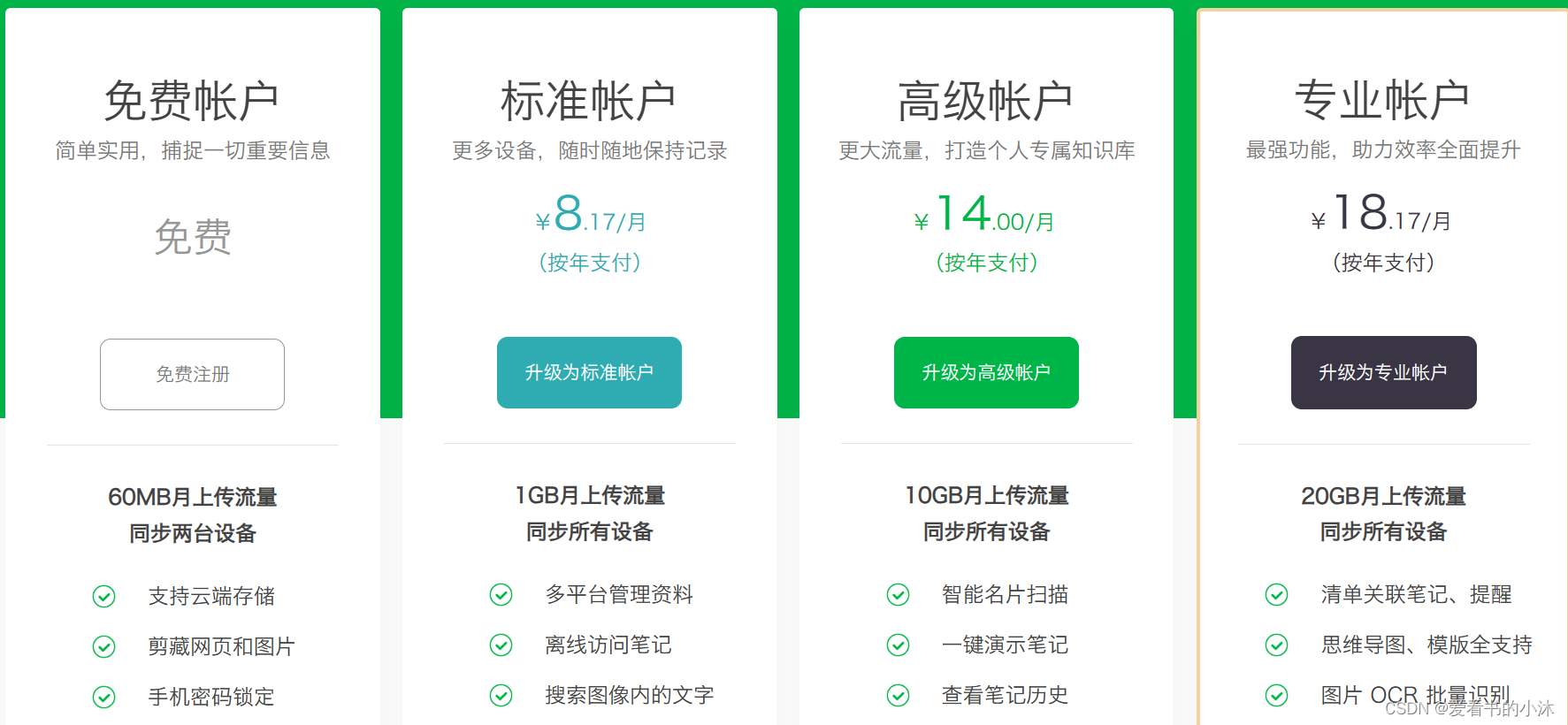
文章目录 1、简介2、微软Office在线文档2.1 功能简介2.2 使用费用2.3 用户体验 3、石墨文档3.1 功能简介3.2 使用费用 4、腾讯文档4.1 功能简介4.2 使用费用 5、语雀5.1 功能简介5.2 使用费用 6、飞书6.1 功能简介6.2 使用费用 7、印象笔记7.1 功能简介7.2 使用费用 结语 1、简…...

「工具|数据接口」免费公开的REST API 如何借助github搭建自己的fake API接口
本文主要介绍日常开发、测试、教学或者分享中,可能遇到的模拟数据问题。分享免费开发的测试数据接口,以及如何利用github快速搭建定制化的接口数据,避免使用真实数据的风险以及自己现编数据的麻烦。 文章目录 一、场景说明二、免费公开的Fak…...

leetcode 18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复): 0 < a,…...

树上背包问题动态规划
目录 树状动态规划概述 示例 求解思路 树状动态规划概述 树状动态规划(Tree DP)是一种在树结构上进行动态规划的方法。在树状DP中,我们利用树的特殊结构性质,通过递归地向下更新子节点的状态,最终得到整个树的最…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
