leetcode 18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。

// 给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]]
// (若两个四元组元素一一对应,则认为两个四元组重复):
// nums[a] + nums[b] + nums[c] + nums[d] = target
// -1
// 1 1 -1 -2 -> -2 -1 1 1
// -2 + (-1) = -3
// -1 1 2 2
// -1+1 = 0class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> result;sort(nums.begin(),nums.end());int sum = 0;int left,right;for(int k=0;k<nums.size();k++) {// 剪枝处理if(nums[k] > target && nums[k] >= 0) break;// 正确去重a方法if(k>0 && nums[k] == nums[k-1]) continue;for(int i = k + 1;i < nums.size();i++) {// 2级剪枝处理 ? 什么时候会出现这种情况if(nums[k] + nums[i] > target && nums[k] + nums[i] >= 0) {// [1,0,-1,0,-2,2]// -2 -1 0 0 1 2 // 剪枝:-1 2// 剪枝: 0 1// 因为只要 nums[k] + nums[i] > target,那么 nums[i] 后面的数都是正数的话,就一定 不符合条件了。cout<< nums[k] <<" "<< nums[i] <<endl;cout<<"2级剪枝处理?"<<endl;break;}// 对nums[i]去重if(i > k+1 && nums[i] == nums[i-1]) continue;left = i + 1;right = nums.size() - 1;while(right > left) {sum = nums[k] + nums[i] + nums[left] + nums[right];if((long)sum > target) right--;else if((long)sum < target) left++;else {result.push_back(vector<int>{nums[k],nums[i],nums[left],nums[right]});// 对nums[left] 和 nums[right] 去重while(right > left && nums[right] == nums[right-1]) right--;while(right > left && nums[left] == nums[left-1]) left++;// 找到答案时,双指针同时收缩right--;left++;}}}}return result;}
};
相关文章:

leetcode 18. 四数之和
给你一个由 n 个整数组成的数组 nums ,和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] (若两个四元组元素一一对应,则认为两个四元组重复): 0 < a,…...

树上背包问题动态规划
目录 树状动态规划概述 示例 求解思路 树状动态规划概述 树状动态规划(Tree DP)是一种在树结构上进行动态规划的方法。在树状DP中,我们利用树的特殊结构性质,通过递归地向下更新子节点的状态,最终得到整个树的最…...

linux查看进程对应的线程(数)
首先,top或ps查看进程列表,确定要查看的进程pid,如下面40698 查看进程的线程情况 查看进程:top -p 40698 查看线程:top -p 40698 -d 3 -H 其中-d是刷新频率 可看到此进程共211个线程,运行中的是211个。…...

Python中的桌面应用开发库有哪些?
Python中有几个受欢迎的桌面应用开发库。以下是其中一些: Tkinter:这是Python的标准GUI库,它提供了构建简单的桌面应用程序的基本组件和功能。 PyQt:这是一个成熟的、功能强大的跨平台图形用户界面框架,它是Python绑定…...
【大数据】Neo4j 图数据库使用详解
目录 一、图数据库介绍 1.1 什么是图数据库 1.2 为什么需要图数据库 1.3 图数据库应用领域 二、图数据库Neo4j简介 2.1 Neo4j特性 2.2 Neo4j优点 三、Neo4j数据模型 3.1 图论基础 3.2 属性图模型 3.3 Neo4j的构建元素 3.3.1 节点 3.3.2 属性 3.3.3 关系 3.3.4 标…...

Windows11系统C盘用户文件夹下用户文件夹为中文,解决方案
说明: 1. 博主电脑为Windows11操作系统,亲测有效,修改后无任何影响,软件都可以正常运行! 2. Windows10系统还不知道可不可行,因为Windows11的计算机管理中没有本地用户和组,博主在csdn上看到很…...
)
Python正则表达式(re)
正则表达式,又称规则表达式,(Regular Expression,在代码中常简写为regex、regexp或RE),是一种文本模式,包括普通字符(例如,a 到 z 之间的字母)和特殊字符(称为…...
【PyTorch 08】如果要手动安装对应的包
例如有时候我们要下载 PyG ,但是需要手动下载,需要进行以下步骤: 网站链接:https://data.pyg.org/whl/ 首先查看当前安装好的Pytorch版本和对应的cuda版本 1. pip list:查看torch版本 2. torch.version.cuda…...
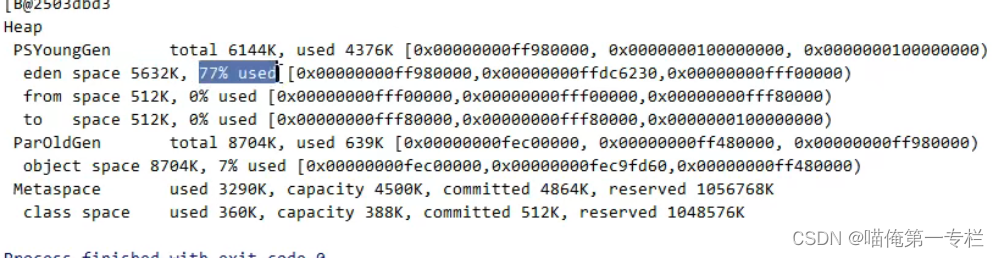
黑马JVM总结(十二)
(1)五种引用_强软弱 实线箭头表示强引用,虚心线表示软弱虚终结器引用 在平时我们用的引用,基本都为强引用 ,比如说创建一个对象通过运算符赋值给了一个变量,那么这个变量呢就强引用了刚刚的对象 强引用的…...
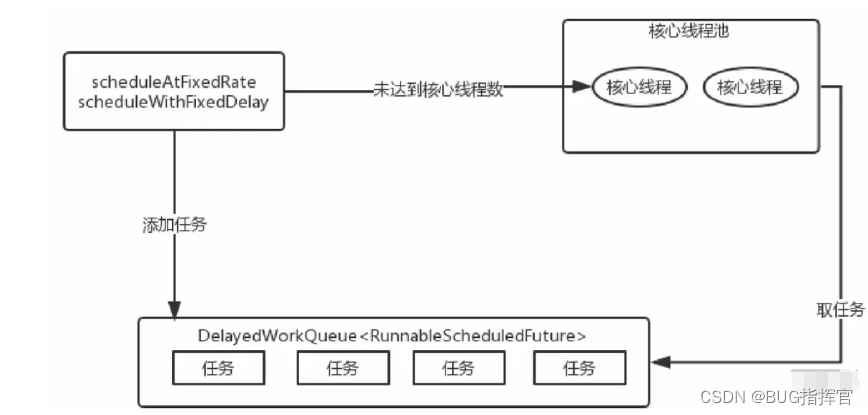
彻底搞懂线程池原理以及创建方式
1. 为什么要使用线程池 在实际使用中,线程是很占用系统资源的,如果对线程管理不善很容易导致系统问题。因此,在大多数并发框架中都会使用线程池来管理线程,使用线程池管理线程主要有如下好处: 降低资源消耗。通过复用…...
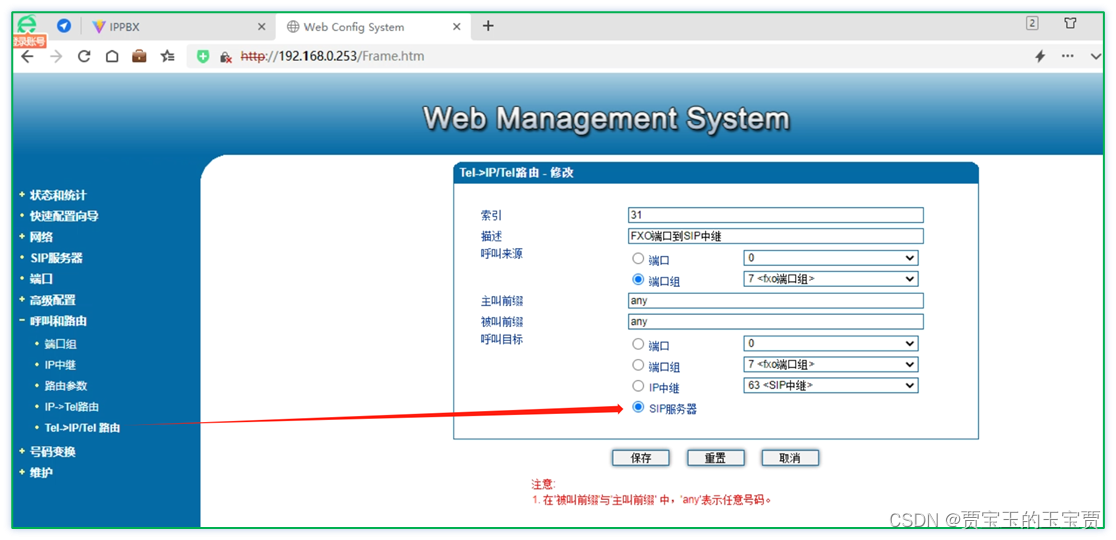
FreeSWITCH 1.10.10 简单图形化界面9 - 鼎兴FXO网关SIP中继内网IPPBX落地
FreeSWITCH 1.10.10 简单图形化界面9 - 鼎兴FXO网关SIP中继内网IPPBX落地 0、 界面预览1、创建一个话务台2、创建PBX SIP中继并设置呼入权限3、设置呼出规则4、设置分机呼出权限5、设置FXO 网关相关信息6、设置FXO网关端口组呼入号码7、设置FXO网关的SIP中继8、设置FXO网关呼叫…...
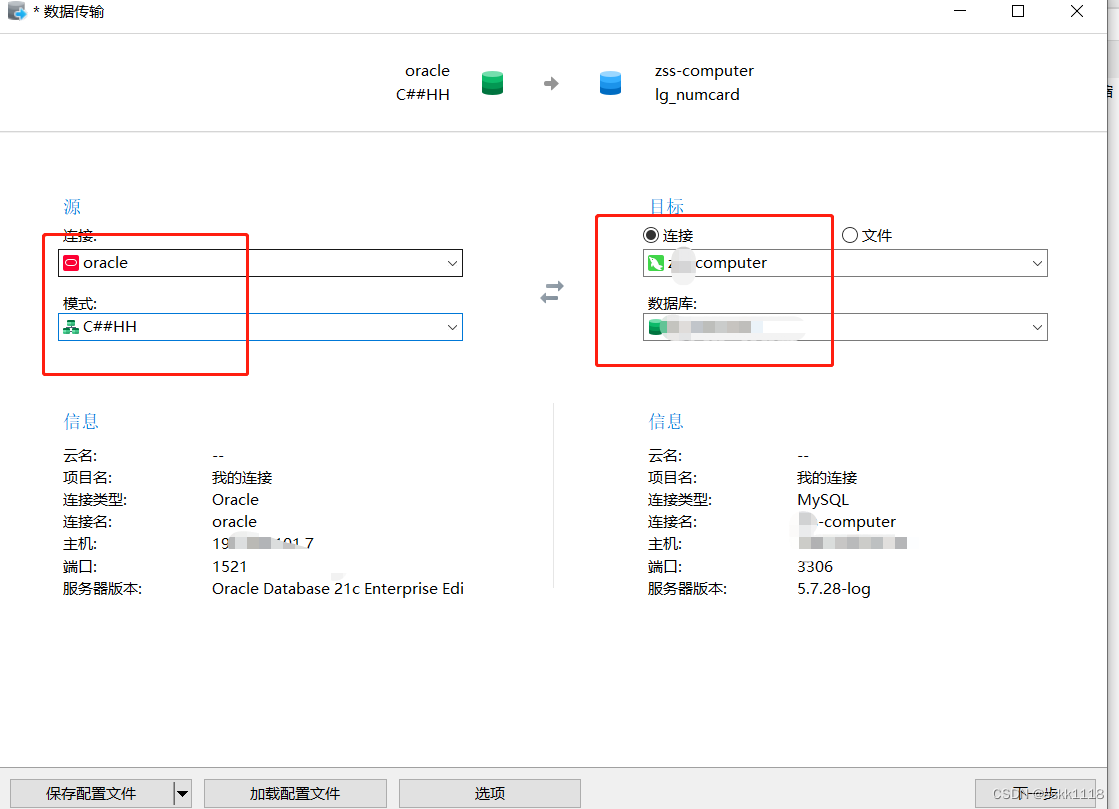
Oracle数据如何迁移导入到MySQL
使用Navicat工具建立数据连接,进行数据传输 1、打开Navicat工具,分别连接Oracle数据库和MySQL数据库。 2、连接源选择你的oracle数据,目标选mysql 即可成功导入...

卡尔曼滤波(Kalman Filter)原理浅析-数学理论推导-1
目录 前言数学理论推导1. 递归算法2. 数学基础结语参考 前言 最近项目需求涉及到目标跟踪部分,准备从 DeepSORT 多目标跟踪算法入手。DeepSORT 中涉及的内容有点多,以前也就对其进行了简单的了解,但是真正去做发现总是存在这样或者那样的困惑…...

Linux 文件创建、查看
touch、cat、more命令 ①touch命令——创建文件 ②cat命令——查看文件内容全部显示 这是txt.txt文件内容 使用cat命令查看 ③more命令——查看文件内容支持翻页 在查看的过程中,通过空格翻页,通过q退出查看...
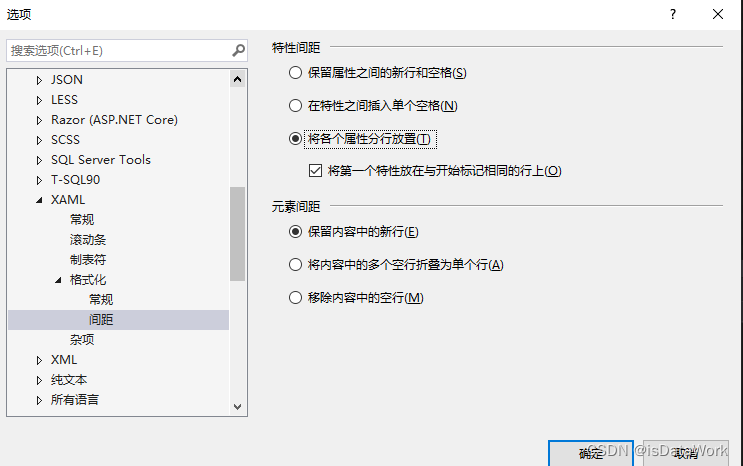
WPF 如何让xmal的属性换行显示 格式化
WPF 如何让UI的xmal 按照下面的格式化显示 首先格式化显示在VS中的快捷键是 Ctrl KD 然后需要配置,工具 选项 -文本编辑器 -xmal -格式化-间距 更改成如下就可以了...

Linux学习之MySQL主从复制
MySQL配置一主一从 环境准备: 两台服务器: Master:192.168.88.53,Slave:192.168.88.54 在两台服务器上安装mysql-server # 配置主服务器192.168.88.53 # 启用binlog日志 [rootmysql53 ~]# yum -y install mysql-ser…...
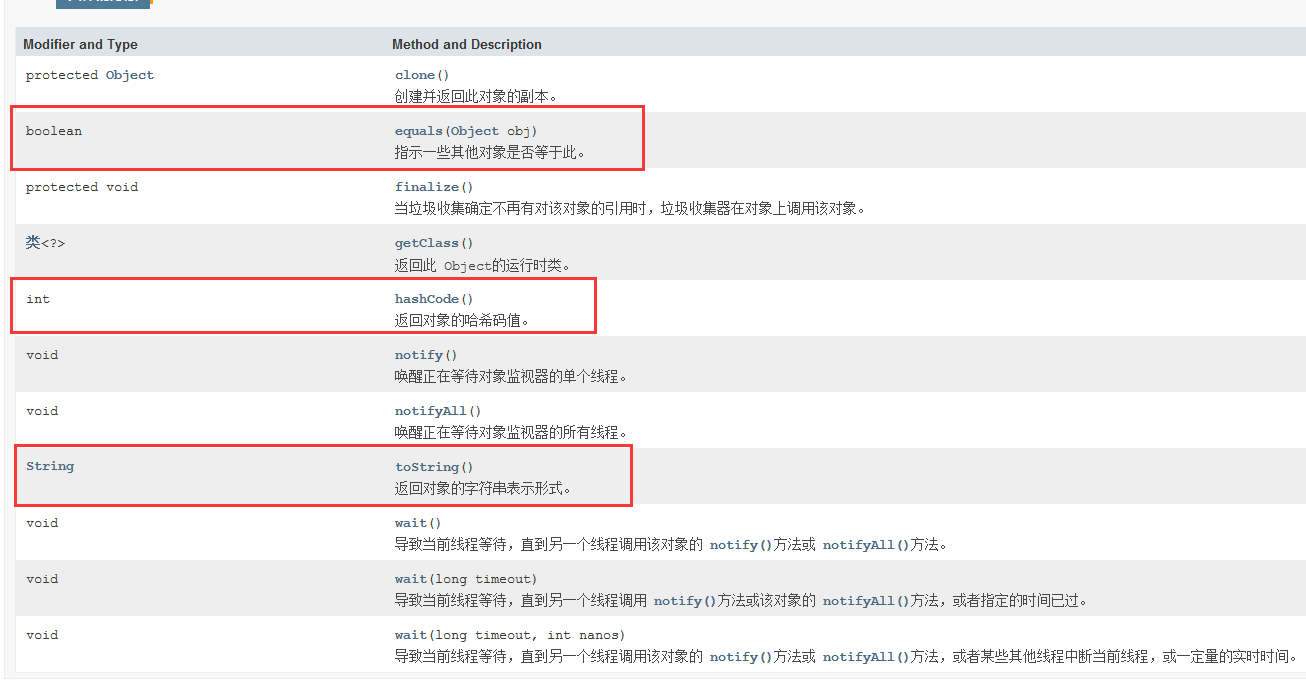
【JavaSE笔记】抽象类与接口
一、抽象类 1、概念 在面向对象的概念中,所有的对象都是通过类来描绘的,但是反过来,并不是所有的类都是用来描绘对象的,如果一个类中没有包含足够的信息来描绘一个具体的对象,这样的类就是抽象类。 package demo2…...
详谈操作系统中的内核态和用户态
不知道大家有没有思考过这样一个问题:什么是处理器(CPU)的状态?🤔 其实CPU和人一样,没有执行程序的时候,是没有什么状态的,当它执行的程序是用户程序的时候就叫用户态,当执行的程序是操作系统的代码时就叫系统态或者内…...

OpenWrt KernelPackage分析
一. 前言 KernelPackage是OpenWrt用来编译内核模块的函数,其实KernelPackage后面会调用BuildPackage,这里会一块将BuildPackage也顺便分析,本文以gpio-button-hotplug驱动模块为例,讲解整个编译过程。 gpio-button-hotplug驱动编译…...
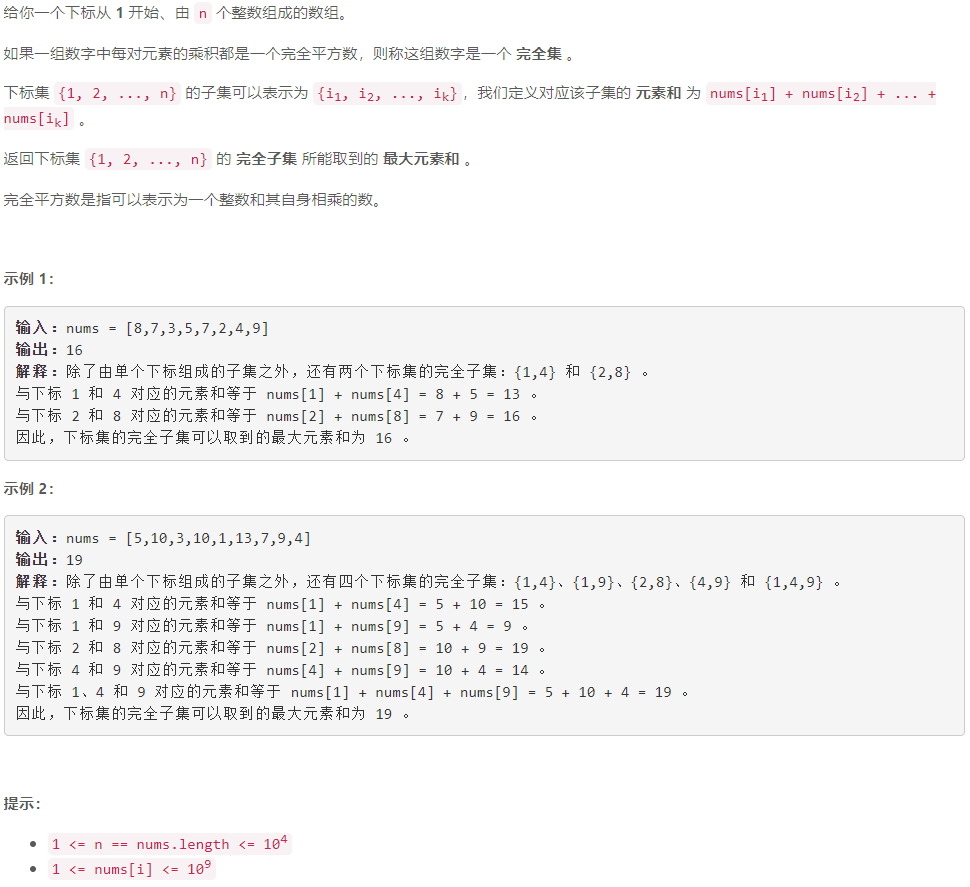
第 363 场 LeetCode 周赛题解
A 计算 K 置位下标对应元素的和 模拟 class Solution { public:int pop_cnt(int x) {//求x的二进制表示中的1的位数int res 0;for (; x; x >> 1)if (x & 1)res;return res;}int sumIndicesWithKSetBits(vector<int> &nums, int k) {int res 0;for (int i…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
