数据聚类分析
K均值
1.1 数据来源(随机生成)
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobsX, y = make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)
# plt.scatter(X[:, 0], X[:, 1], c='white', marker='o', edgecolors='black', s=50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50)
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.grid()
plt.tight_layout()
plt.savefig('./fig/data presentation.png')
plt.show()

make_blobs的用法
make_blobs函数是为聚类产生数据集,产生一个数据集和相应的标签
- n_samples:表示数据样本点个数,默认值100
- n_features:是每个样本的特征(或属性)数,也表示数据的维度,默认值是2
- centers:表示类别数(标签的种类数),默认值3
- cluster_std表示每个类别的方差,例如我们希望生成2类数据,其中一类比另一类具有更大的方差,可以将cluster_std设置为[1.0,3.0],浮点数或者浮点数序列,默认值1.0
- center_box:中心确定之后的数据边界,默认值(-10.0, 10.0)
- shuffle :将数据进行洗乱,默认值是True
- random_state:官网解释是随机生成器的种子,可以固定生成的数据,给定数之后,每次生成的数据集就是固定的。若不给定值,则由于随机性将导致每次运行程序所获得的的结果可能有所不同。在使用数据生成器练习机器学习算法练习或python练习时建议给定数值。
1.2 手写Kmeans
K均值算法的4个步骤:
- 从所有样本中随机挑选k个样本质心作为初始簇的中心;
- 将每个样本分配给最近的质心;
- 更新质心,新的质心为已分配样本的中心(假设样本呢特征值是连续的);
- 重复步骤2和步骤3,直到每个样本的归属不再发生变化,或者迭代次数达到了用户定义的容差或最大迭代次数。
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobsdef plot_data(X, y, centroids, t):plt.scatter(X[:, 0], X[:, 1], c=y, s=50)plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', c='red', s=150)plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.grid()plt.title('t={}'.format(t))plt.tight_layout()plt.savefig('./fig/t={}.png'.format(t))plt.show()returndef distEclud(arrA, arrB):d = arrA - arrBdist = np.sum(np.power(d, 2), axis=1)return pow(dist, 0.5)def randCent(dataSet, k):n = dataSet.shape[1]data_min = dataSet.iloc[:, :n].min()data_max = dataSet.iloc[:, :n].max()data_cent = np.random.uniform(data_min, data_max, (k, n))return data_centdef kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):m, n = dataSet.shapecentroids = createCent(dataSet, k)clusterAssment = np.zeros((m, 3))clusterAssment[:, 0] = np.infclusterAssment[:, 1:3] = -1result_set = pd.concat([dataSet, pd.DataFrame(clusterAssment)], axis=1, ignore_index=True)clusterChanged = Truetime = 0plot_data(dataSet.iloc[:, 0:n].values, result_set.iloc[:, -1].values, centroids, time)while clusterChanged:for i in range(m):dist = distMeas(dataSet.iloc[i, :n].values, centroids)result_set.iloc[i, n] = dist.min()result_set.iloc[i, n + 1] = np.where(dist == dist.min())[0]clusterChanged = not (result_set.iloc[:, -1] == result_set.iloc[:, -2]).all()if clusterChanged:cent_df = result_set.groupby(n + 1).mean()centroids = cent_df.iloc[:, :n].valuesresult_set.iloc[:, -1] = result_set.iloc[:, -2]time = time + 1plot_data(result_set.iloc[:, 0:n].values, result_set.iloc[:, -1].values, centroids, time)if time == 1000:breakreturn centroids, result_setX, y = make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)
dataSet = X
dataSet = pd.DataFrame(dataSet)
centroids, result_set = kMeans(dataSet, 3, distMeas=distEclud, createCent=randCent)





代码说明
在执行k-means的时候,需要不断的迭代质心,因此需要两个可迭代容器来完成该目标:
第一个容器用于存放和更新质心,该容器可考虑使用数组来执行,数组不仅可迭代对象,同时数组内不同元素索引位置也可
用于标记和区分各质心,即各簇的编号。
第二个容器泽需要记录、保存和更新各点到质心之间的距离,并能够方便对其进行比较,该容器可以使用一个三列的数组来
执行,其中第一列用于存放最近一次完成后某点到各质心的最短距离,第二列用于存放迭代后根据最短距离得到的代表对应
质心的数值索引,即所属簇,第三类用于存放上一次迭代后的所属簇,后两列用于比较所属簇是否发生变化,确定迭代结束。
1.3 SSE计算
k均值是一种迭代方法,用于最小化簇内误差平方和(Sum of Sqquared Erroe, SSE)。误差平方和有时也被称为簇惯性(cluster inertia),定义如下,
S S E = ∑ i = 1 n ∑ j = 1 k w ( i , j ) ∥ x ( i ) − u ( j ) ∥ 2 2 {\rm{SSE}} = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^k {{w^{(i,j)}}\left\| {{x^{(i)}} - {u^{(j)}}} \right\|_2^2} } SSE=i=1∑nj=1∑kw(i,j) x(i)−u(j) 22
其中 μ ( j ) {\mu ^{(j)}} μ(j)为簇j的质心。如果样本 x ( i ) {x^{(i)}} x(i)在簇j中,则 w ( i , j ) = 1 {w^{(i,j)}} = 1 w(i,j)=1,否则 w ( i , j ) = 0 {w^{(i,j)}} = 0 w(i,j)=0:

"""
函数功能:聚类学习曲线
参数说明:dataSet:原始数据集cluster:K-means聚类方法k:簇的个数
返回:误差平方和SSE
"""
def kcLearningCurve(dataSet, cluster = kMeans,k = 10):n = dataSet.shape[1]SSE = []for i in range(1,k):centroids,result_set = cluster(dataSet,i+1)SSE.append(result_set.iloc[:,n].sum())plt.plot(range(2,k+1),SSE,"--o")return SSE
1.4 手写Kmeans++
import math
import random
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobsdef plot_data(X, y, centroids, t):plt.scatter(X[:, 0], X[:, 1], c=y, s=50)plt.scatter(centroids[:, 0], centroids[:, 1], marker='*', c='red', s=150)plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.grid()plt.title('t={}'.format(t))plt.tight_layout()plt.savefig('./fig2/t={}.png'.format(t))plt.show()returndef distEclud(arrA, arrB):d = arrA - arrBdist = np.sum(np.power(d, 2), axis=1)return pow(dist, 0.5)def euler_distance(point1, point2):"""计算两点之间的欧式距离,支持多维"""distance = 0.0for a, b in zip(point1, point2):distance += math.pow(a - b, 2)return math.sqrt(distance)# 计算最小距离
def get_closest_dist(point, centroids):min_dist = math.inf # 初始设为无穷大for i, centroid in enumerate(centroids):dist = euler_distance(centroid, point)if dist < min_dist:min_dist = distreturn min_distdef kpp_centers(data_set, k):"""从数据集中返回 k 个对象可作为质心"""cluster_centers = []cluster_centers.append(random.choice(data_set))d = [0 for _ in range(len(data_set))]for _ in range(1, k):total = 0.0for i, point in enumerate(data_set):d[i] = get_closest_dist(point, cluster_centers) # 与最近一个聚类中心的距离total += d[i]total *= random.random()for i, di in enumerate(d): # 轮盘法选出下一个聚类中心;total -= diif total > 0:continuecluster_centers.append(data_set[i])breakreturn np.array(cluster_centers)def kMeans(dataSet, k, distMeas=distEclud, createCent=kpp_centers):m, n = dataSet.shapecentroids = createCent(dataSet.values, k)clusterAssment = np.zeros((m, 3))clusterAssment[:, 0] = np.infclusterAssment[:, 1:3] = -1result_set = pd.concat([dataSet, pd.DataFrame(clusterAssment)], axis=1, ignore_index=True)clusterChanged = Truetime = 0plot_data(dataSet.iloc[:, 0:n].values, result_set.iloc[:, -1].values, centroids, time)while clusterChanged:for i in range(m):dist = distMeas(dataSet.iloc[i, :n].values, centroids)result_set.iloc[i, n] = dist.min()result_set.iloc[i, n + 1] = np.where(dist == dist.min())[0]clusterChanged = not (result_set.iloc[:, -1] == result_set.iloc[:, -2]).all()if clusterChanged:cent_df = result_set.groupby(n + 1).mean()centroids = cent_df.iloc[:, :n].valuesresult_set.iloc[:, -1] = result_set.iloc[:, -2]time = time + 1plot_data(result_set.iloc[:, 0:n].values, result_set.iloc[:, -1].values, centroids, time)if time == 1000:breakreturn centroids, result_setX, y = make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)
dataSet = X
dataSet = pd.DataFrame(dataSet)
centroids, result_set = kMeans(dataSet, 3, distMeas=distEclud, createCent=kpp_centers)



Kmeans++的原理可参考:https://blog.csdn.net/kuwola/article/details/124533036
1.5 Scikit-Learn实现k均值聚类
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeansX, y = make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)km = KMeans(n_clusters=3,init="random",n_init=10,max_iter=300,tol=1e-4,verbose=0,random_state=0)
y_km = km.fit_predict(X)
plt.scatter(X[y_km == 0, 0], X[y_km == 0, 1], s=50, c='lightgreen', marker='s', edgecolors='black', label='Cluster 1')
plt.scatter(X[y_km == 1, 0], X[y_km == 1, 1], s=50, c='orange', marker='o', edgecolors='black', label='Cluster 2')
plt.scatter(X[y_km == 2, 0], X[y_km == 2, 1], s=50, c='lightblue', marker='v', edgecolors='black', label='Cluster 3')
plt.scatter(km.cluster_centers_[:, 0], km.cluster_centers_[:, 1], s=250, c='lightblue', marker='*', edgecolors='red',label='Centroids')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.legend(scatterpoints=1)
plt.grid()
plt.tight_layout()
plt.savefig('./fig/k means.png')
plt.show()

1.6 Scikit-Learn实现kMeans++均值聚类
在Scikit-Learn的KMeans对象上使用k均值++算法,只需将参数init设置成,’k-means++'即可。
’k-means++'是参数init的默认值,实际应用中推荐使用。
1.7 Scikit-Learn 肘方法
import os
os.environ["OMP_NUM_THREADS"] = "1"
from matplotlib import pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobsX, y = make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)distortions = []
for i in range(1, 11):km = KMeans(n_clusters=i,init='k-means++',n_init=10,max_iter=300,random_state=0)km.fit(X)distortions.append(km.inertia_)
plt.plot(range(1, 11), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.savefig('./fig2/a.png', dpi=300)
plt.show()

1.8 Scikit-Learn 轮廓分析
import numpy as np
from matplotlib import cm, pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
from sklearn.metrics import silhouette_samplesX, y = make_blobs(n_samples=150,n_features=2,centers=3,cluster_std=0.5,shuffle=True,random_state=0)km = KMeans(n_clusters=3,init='k-means++',n_init=10,max_iter=300,tol=1e-04,random_state=0)
y_km = km.fit_predict(X)cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):c_silhouette_vals = silhouette_vals[y_km == c]c_silhouette_vals.sort()y_ax_upper += len(c_silhouette_vals)color = cm.jet(float(i) / n_clusters)plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0,edgecolor='none', color=color)yticks.append((y_ax_lower + y_ax_upper) / 2.)y_ax_lower += len(c_silhouette_vals)silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--")plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')plt.tight_layout()
plt.savefig('./fig/b.png', dpi=300)
plt.show()

相关文章:

数据聚类分析
K均值 1.1 数据来源(随机生成) import matplotlib.pyplot as plt from sklearn.datasets import make_blobsX, y make_blobs(n_samples150,n_features2,centers3,cluster_std0.5,shuffleTrue,random_state0) # plt.scatter(X[:, 0], X[:, 1], cwhite, markero, edgecolorsbl…...

前 40 个 Microsoft Excel 面试问题答案
1)什么是 Microsoft Excel? Microsoft Excel 是一个电子电子表格应用程序,使用户可以使用按行和列细分的电子表格系统,使用公式存储,组织,计算和处理数据。 它还提供了使用外部数据库进行分析,…...

ros2学习笔记:shell环境变量脚本setup.bash[-z][-n][-f]参数作用
-n作用 [ -n 字符串 ] or [ 字符串 ] 字符串的长度为非零(有内容)则为真。加-n与不加-n结果相同。 -z作用 [ -z 字符串 ] 字符串的长度为零则为真。 字符串为空即NULL时为真,与上面的-n相反。 -f作用 [ -f FILE ] 如果 FILE 存在且是一…...

xss渗透(跨站脚本攻击)
一、什么是XSS? XSS全称是Cross Site Scripting即跨站脚本,当目标网站目标用户浏览器渲染HTML文档的过程中,出现了不被预期的脚本指令并执行时,XSS就发生了。 这里我们主要注意四点: 1、目标网站目标用户; 2、浏览…...
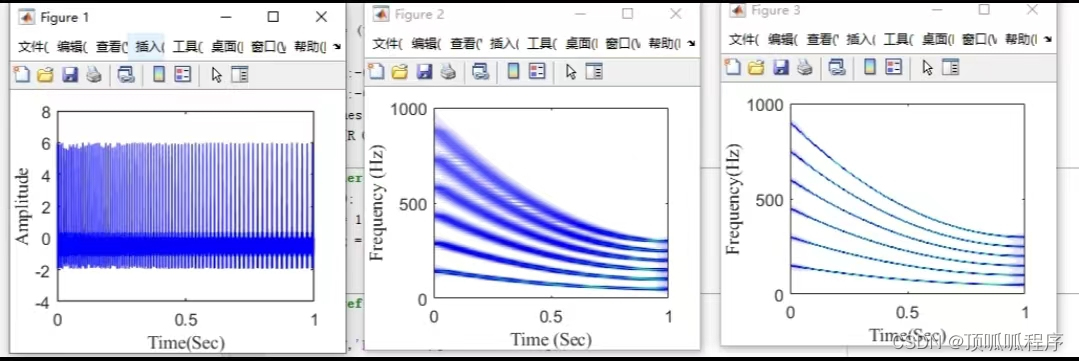
9参数化重采样时频变换,基于MATLAB平台,程序已调通,可直接替换数据进行分析。
参数化重采样时频变换,基于MATLAB平台,程序已调通,可直接替换数据进行分析。 9matlab参数化重采样时频变换 (xiaohongshu.com)...
RK3568平台开发系列讲解(调试篇)系统运行相关频率设置
🚀返回专栏总目录 文章目录 一、CPU 频率设置二、DDR 频率设置三、NPU 频率设置沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 CPU 默认是 interactive 状态,它会根据 CPU 使用率和目标负载来动态地调整 CPU 频率。为获得更高运行速度或者性能评估,我们需要手动固…...

嵌入式:驱动开发 Day2
作业:字符设备驱动,完成三盏LED灯的控制 驱动代码: mychrdev.c #include <linux/init.h> #include <linux/module.h> #include <linux/fs.h> #include <linux/uaccess.h> #include <linux/io.h> #include &q…...
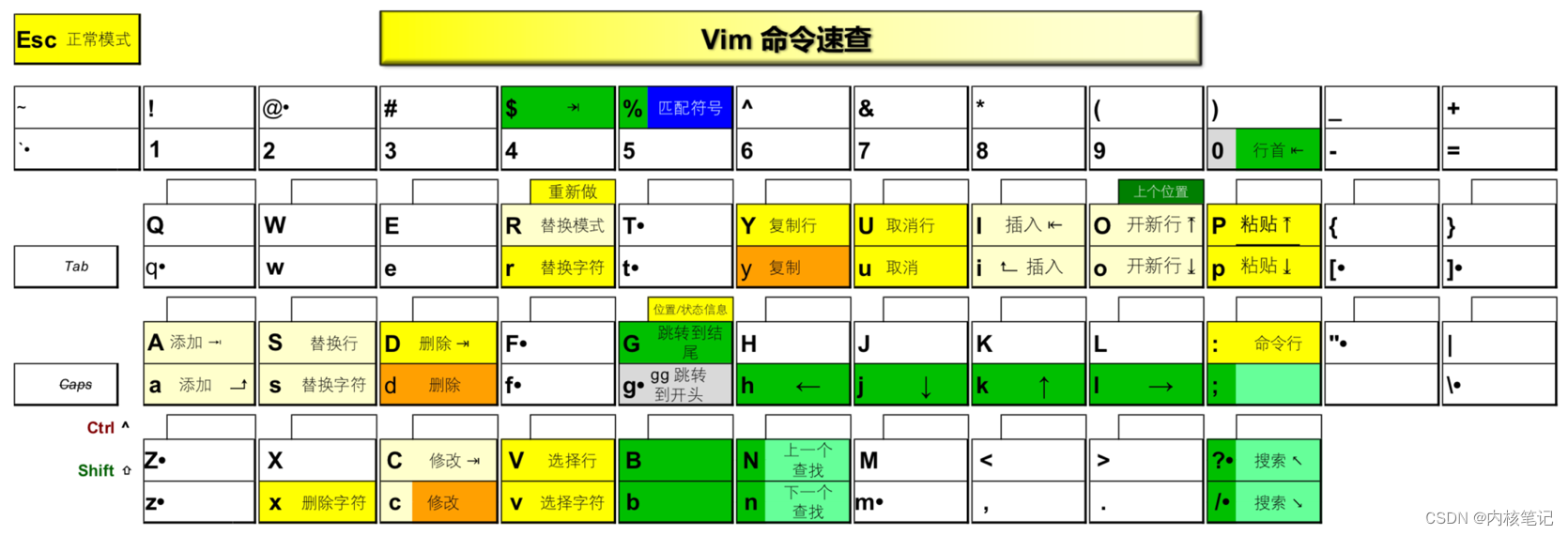
RK3399平台开发系列讲解(入门篇)VIM的基础命令
🚀返回专栏总目录 文章目录 一、Vim 命令速查二、其他命令三、Vim模式沉淀、分享、成长,让自己和他人都能有所收获!😄 📢 本篇将介绍Vim相关命令。 一、Vim 命令速查 简单说明一下,这张图上展示了一个键盘。图中的“•”表示,单个字母不是完整的命令,必须再有进一步…...

Rocky Linux 安装图解(替代centos)服务器+桌面
centos自从20年底转变为不稳定版本后,有很多替代方案 经过近3年的发展,rocky linux算是一个比较好的选择,一是依照red hat企业版来做,二是rocky的发起者也是centos的创始人 如果想安装debian,可以参考:deb…...

webpack 基础配置
常见配置 文件打包的出口和入口webpack如何开启一台服务webpack 如何打包图片,静态资源等。webpack 配置 loader配置 plugin配置sourceMap配置 babel 语法降级等 接下来 , 我们先从webpack的基本配置 开始吧! 在准备 配置之前 , 搭建一个 …...
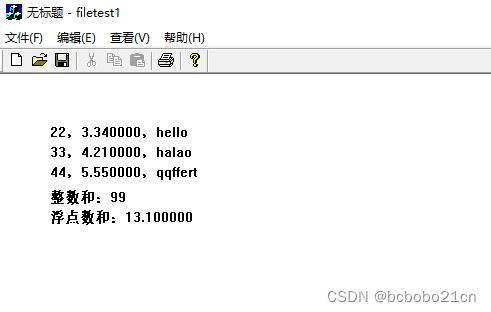
C语言和mfc按格式读取文件数据
fscanf()函数的功能是从文件中按格式读取一个或多个数据; 例如文件中有一行数据, 22 3.34 hello 则使用 fscanf(fp, "%d%f%s", &a, &f, str) 可一次读取整型、浮点、字符串三个数据; 此函数位于C标准库头文件<stdio…...
)
SQLyog 各版本下载与安装(目前最新版本为13.2.0)
文章目录 一、SQLyog Ultimate 各版本下载1. For Windows x642. For Windows x86 二、SQLyog Community 各版本下载1. For Windows x642. For Windows x863. For Linux x86_644. For Linux i386 三 、SQLyog 安装四、如何解决SQLyog试用期到期问题五、最后 数据库可视化工具&am…...

CopyOnWrite 容器
CopyOnWrite容器是Java并发包中提供的一种特殊类型的集合,它的特点是在进行修改操作时不会修改原始容器,而是创建一个新的容器副本进行修改,这样可以避免并发修改异常(ConcurrentModificationException)。 主要的CopyOnWrite容器包括: CopyOnWriteArrayList:这是一个基…...

云服务部署:AWS、Azure和GCP比较
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

Linux安装Ansible管理工具
条件情况说明 准备4台机器,是单master集群安装 192.168.186.128 ansible 192.168.186.129 node1 192.168.186.130 node2 192.168.186.131 node3 #永久修改主机名 hostnamectl set-hostname ansible && bash #在ansible上操作 hostnamectl set-hostname n…...
七天学会C语言-第二天(数据结构)
1. If 语句: If 语句是一种条件语句,用于根据条件的真假执行不同的代码块。它的基本形式如下: if (条件) {// 条件为真时执行的代码 } else {// 条件为假时执行的代码 }写一个基础的If语句 #include<stdio.h> int main(){int x 10;…...

高级功能的PID控制器在电离规等真空计线性化处理中的应用
摘要:针对高真空度用皮拉尼计和电离规信号的非线性和线性两种输出规格,为改进高真空度的测量和控制精度,本文提出了线性化处理的解决方案。解决方案的关键是采用多功能超高精度的真空压力控制器,具体内容一是采用控制器自带的最小…...
)
元素全排列问题的新思路(DFS,递归,计数器)
目录 前言 1,普通DFS实现1~n的元素全排列 2,计数器DFS实现重复元素全排列 总结 前言 我们之前看到的全排列问题的解法都是通过交换法达到的,去重的效果也是通过判断当前元素前是否有相同元素来实现,今天我们带来一个全新的思路…...

机器学习 day35(决策树)
决策树 上图的数据集是一个特征值X采用分类值,即只取几个离散值,同时也是一个二元分类任务,即标签Y只有两个值 上图为之前数据集对应的决策树,最顶层的节点称为根节点,椭圆形节点称为决策节点,矩形节点称…...

小程序引入vant-Weapp保姆级教程及安装过程的问题解决
小知识,大挑战!本文正在参与“程序员必备小知识”创作活动。 本文同时参与 「掘力星计划」,赢取创作大礼包,挑战创作激励金 当你想在小程序里引入vant时,第一步:打开官方文档,第二步ÿ…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
