计数排序与基数排序
计数排序与基数排序
计数排序
计数排序:使用一个数组记录序列中每一个数字出现的次数,将该数组的下标作为实际数据,元素的值作为数据出现的次数。例如对于序列[3,0,1,1,3,3,0,2],统计的结果为:
0出现的次数:2次
1出现的次数:2次
2出现的次数:1次
3出现的次数:3次
依据出现的次数就可以构建出排序之后的序列
void CountSort(vector<int>& nums) {int minNum = nums.front();int maxNum = nums.front();for (int num : nums) {minNum = std::min(minNum, num);maxNum = std::max(maxNum, num);}int helpSize = maxNum - minNum + 1;int* help = new int[helpSize] {0};//例如最大值为10,最小值为5,需要开辟的数组大小是10-5+1for (int num : nums) {help[num - minNum]++;//统计次数}nums.clear();for (int i = 0; i < helpSize; i++) {while (help[i]--) {nums.push_back(i + minNum);}}delete[] help;
}
计数排序的时间复杂度和空间复杂度
时间复杂度:O(N+max-min),其中max为数组中的最大元素,min为数组中的最小元素。计数排序需要遍历原数组一趟,得到原数组的最大值和最小值从而决定需要开辟的辅助数组的大小,还需要遍历辅助数组得到有序序列
空间复杂度:O(max-min),取决于数组中最大值和最小值的差
计数排序适用于数据量很大,但是数据分布比较密集的场景,例如有1亿个数,它们都在[20,1000]范围,此时就可以使用计数排序,与其它排序算法相比(例如快排、冒泡),计数排序是一种非比较排序
基数排序
在计数排序中,对于数据较为分散的场景,所需开辟的额外空间较大,例如序列[1,56,26,9999,7],若使用计数排序,需要额外开辟一个大小为9999的数组,但是原数组只有5个数需要进行排序,在这种情况下,可以考虑使用基数排序
基数排序也是一种非比较排序,基本思想是:先将原序列按照个位进行排序,在按照十位进行排序……依次类推,直到序列完全有序,以[1,56,26,9999,7]为例,流程如下:

基数排序的轮数取决于序列中最大值的位数,在进行基数排序时,位数小的数字一定在位数大的数字的前面,例如上图中7虽然在进行第一轮排序完成后处于56的后面,但是当完成第二轮排序后7处于56的前面,因为7的十位为0
如何提取一个数字的个位、十位、百位?
方案一:使用to_string将该数字转化为字符串,依次进行提取
方案二:定义一个offset变量,初始为1,将(num/offset)%10,得到个位,每进行一轮,将offset*10
int num = 3675;
int offset = 1;
int bitNum;
while (bitNum=num / offset) {cout << bitNum % 10 << ' ';offset *= 10;
}
cout << endl;
基数排序的桶
在进行基数排序时一般使用队列作为基数排序的桶,对10进制数字进行排序就需要准备9个队列
void RadixSortByQueue(vector<int>& nums, int bits, int BASE = 10) {//使用队列作为桶进行基数排序//bits表示序列中的最大值的位数//BASE表示多少进制vector<queue<int>> Queues;Queues.resize(BASE);int offset = 1;for (int offset = 1; bits > 0; bits--, offset *= BASE) {//例如最大值为156,则进行3轮for (int num : nums) {int bitNum = (num / offset) % BASE;//得到个位/十位/百位……的数Queues[bitNum].push(num);}//按照个位/十位/百位……排好的数已经放入Queues中nums.clear();for (auto& Queue : Queues) {while (!Queue.empty()) {nums.push_back(Queue.front());Queue.pop();}}}
}
基数排序的优化
前缀数量分区:以序列[1,56,26,9999,7]为例,个位数分别是1,6,6,9,7,可以得到的前缀信息如下
个位数<=1的数据数量:1
个位数<=6的数据数量:3
个位数<=7的数据数量:4
个位数<=9的数据数量:5
那么在每一轮按照特定位进行排序时就不需要使用队列,直接开一个和原始数组等规模的辅助数组help即可,将[1,56,26,9999,7]按照个位进行排序,对于数字7,个位为7,由于个位数<=7的数据数量是4,所以7直接放到help数组中下标为3的位置,此时原序列中的7已经放到help数组中,原序列中个位数<=7的数据数量减少一个,变为3,以此类推,直到原序列中的数据全部按照规则转移到help数组中,此时help数组中的数据就是按照位排序好的数据
void RadixSort(vector<int>& nums, int bits, int BASE = 10) {//bits表示序列中的最大值的位数//BASE表示多少进制int* counts = new int[BASE] {0};int* help = new int[nums.size()]{ 0 };int offset = 1;for (int offset = 1; bits > 0; bits--, offset *= BASE) {memset(counts, 0, sizeof(int) * BASE);for (int num : nums) {int bitNum = (num / offset) % BASE;counts[bitNum]++;//先统计个数}for (int i = 1; i < BASE; i++) {counts[i] += counts[i - 1];//统计前缀数量}for (int i = nums.size() - 1; i >= 0; i--) {int bitNum = (nums[i] / offset) % BASE;help[--counts[bitNum]] = nums[i];}memcpy(nums.data(), help, sizeof(int) * nums.size());}delete[] help;delete[] counts;
}
为什么需要从后往前遍历向help数组中填数据?
以[1,99,7]为例,在排个位数时,可以从后往前,也可以从前往后,没有影响,个位数排完之后,得到[1,7,99],但是在排十位数时,必须从后往前,否则就会打乱1和7的顺序,因为1和7的十位都是0,十位<=0的数的个数是2,7是最后一个十位<=的数,因此在遍历时需要从后往前遍历排到靠后位置.
基数排序的拓展
如果原序列中存在负数,如何进行基数排序?
将原序列中的所有数字加上最小值的绝对值,在进行基数排序,将排完序的结果在减去原来最小值的绝对值。如果存在溢出问题,需要考虑使用long long类型。
void RadixSortContainMinus(vector<int>& nums, int BASE = 10) {int minNum = nums[0];for (int num : nums) {minNum = std::min(minNum, num);}int maxNum = 0;for (int& num : nums) {num -= minNum;maxNum = std::max(maxNum, num);}int bits = 1;while (maxNum / BASE) {bits++;maxNum /= BASE;}RadixSort(nums, bits, BASE);for (int& num : nums) {num += minNum;}
}
如果需要排序的数字不是十进制,如何使用基数排序实现?
若需要排序的数字不是10进制,只需要修改BASE即可,其它思路一致,例如需要排序的数字是16进制,那么counts数组的大小定为16即可,统计每一位在0~f的数量,依然使用前缀分区技巧
基数排序的时间复杂度
基数排序的时间复杂度为O(m*n),其中m表示原序列中最大值的位数,n表示数据量,因为要根据位数确定排多少轮。基数排序的空间复杂度为O(m+n),需要使用一个help数组和一个counts数组,其中counts数组用于统计个数,help数组用于进行保存这一轮排序完毕的数据.
相关文章:

计数排序与基数排序
计数排序与基数排序 计数排序 计数排序:使用一个数组记录序列中每一个数字出现的次数,将该数组的下标作为实际数据,元素的值作为数据出现的次数。例如对于序列[3,0,1,1,3,3,0,2],统计的结果为: 0出现的次数…...

Mysql—表操作
目录 1、linux中数据库表名区分大小写,windows不区分2、创建数据库表3、外键4、查看数据表结构5、修改表5.1、修改表名5.2、添加字段5.3、指定位置添加字段5.4、修改字段名称5.5、修改字段类型5.6、修改字段位置5.7、删除字段5.8、修改表存储引擎5.9、删除外键 1、l…...

SpringCloud——微服务
微服务技术栈 在之前的开发过程中,我们将所有的服务都部署在一台服务器中,当我们的服务开始越来越多,业务越来越复杂,当一台服务器不能承担我们的业务的时候,就需要将不同的业务分开部署在不同的服务器上,…...
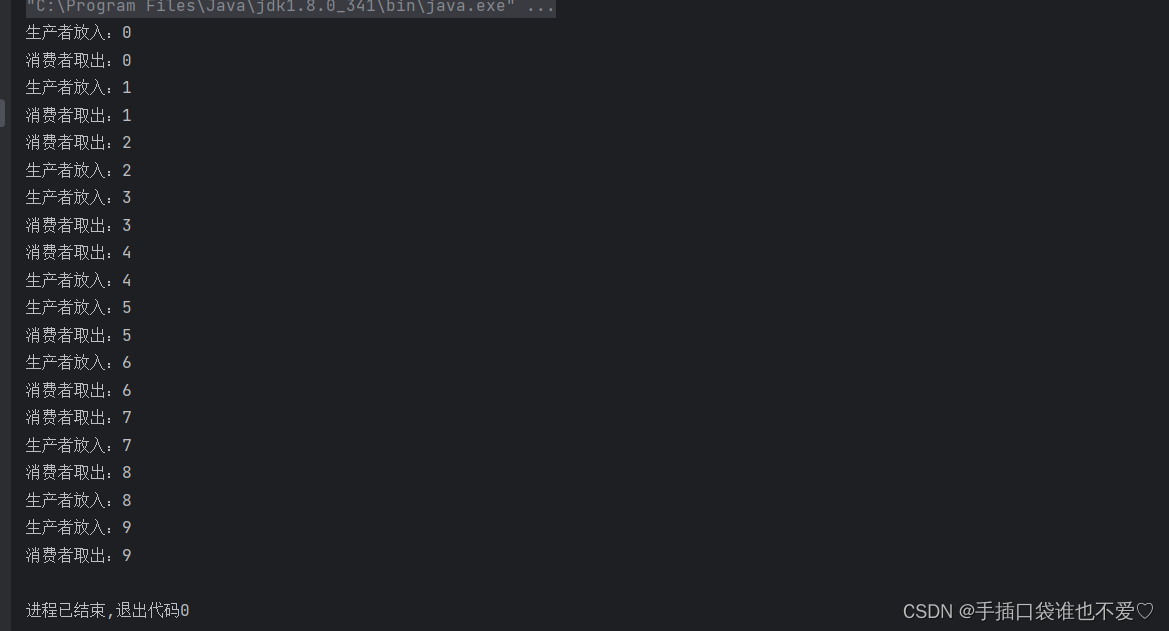
深入理解Java单例模式和优化多线程任务处理
目录 饿汉模式懒汉模式单线程版多线程版双重检查锁定 阻塞队列 单例模式能保证某个类在程序中只存在唯一一份实例, 而不会创建出多个实例,并提供一个全局访问点。 饿汉模式 类加载的同时,创建实例。 class Singleton {private static final Singlet…...

已解决 Kotlin Error: Type mismatch: inferred type is String but Int was expected
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页: 🐅🐾猫头虎的博客🎐《面试题大全专栏》 🦕 文章图文并茂🦖…...
Web应用系统的小安全漏洞及相应的攻击方式
写作目的 本文讲述一个简单的利用WebAPI来进行一次基本没有破坏力的“黑客”行为。 主要目的如下: 了解什么叫安全漏洞 知道什么是api 了解一些获取api的工具 通过对API的认识了解白盒接口测试基本概念和技术 免责声明: 本文主要是以学习交流为目的&a…...

git工具下载和安装
(1)从git官网下载安装包 然后安装 https://git-scm.com/downloads (2)git 学习参考官方的资料 https://git-scm.com/book/en/v2...
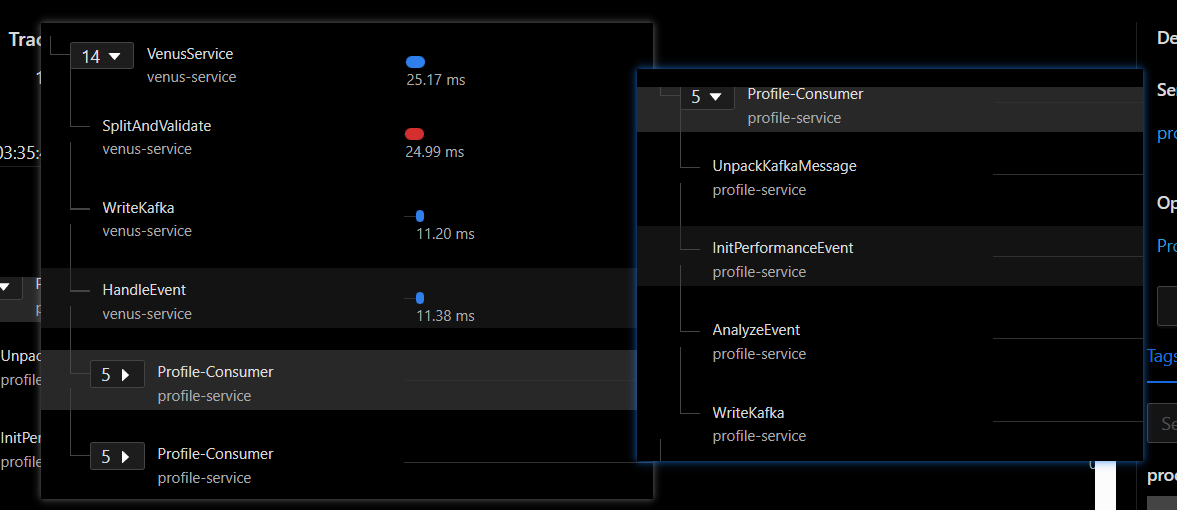
腾讯mini项目-【指标监控服务重构】2023-08-04
今日已办 关于 span-references 的调研 https://github.com/DataDog/dd-trace-js/issues/1761 https://github.com/open-telemetry/opentelemetry-specification/blob/874a451e7f6ac7fc54423ee3f03e5394197be35b/specification/compatibility/opentracing.md#span-references h…...
怎么推广自己抖店的商品?最适合0经验新手操作的办法,来看看
我是王路飞。 抖店开通后,想要把自己店铺的商品卖出去,就需要进行推广了。 但是怎么推广呢? 要么利用抖音的搜索和推荐流量,获取曝光,实现点击和转化。 不过这种玩法有个弊端,就是需要你有一定的电商经…...
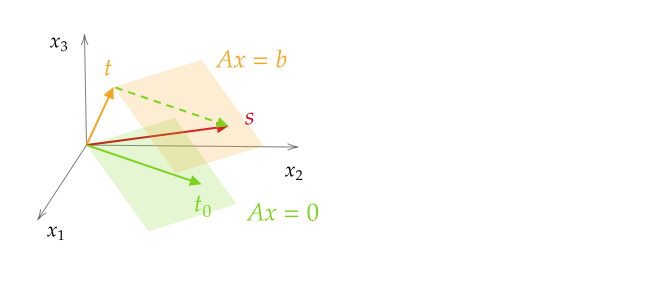
线性代数的本质(三)——线性方程组
文章目录 线性方程组高斯消元法初等行变换线性方程组的解向量方程齐次线性方程组的解非齐次线性方程组的解 线性方程组 高斯消元法 客观世界最简单的数量关系是均匀变化的关系。在均匀变化问题中,列出的方程组是一次方程组,我们称之为线性方程组(Linea…...

轻量级性能测试工具 wrk 如何使用?
项目设计之初或者是项目快要结束的时候,大佬就会问我们,这个服务性能测试的结果是什么,QPS 可以达到多少,RPS 又能达到多少?接口性能可以满足未来生产环境的实际情况吗?有没有自己测试过自己接口的吞吐量&a…...

WebGL 视图矩阵、模型视图矩阵
目录 立方体由三角形构成 视点和视线 视点、观察目标点和上方向 视点: 观察目标点: 上方向: 在WebGL中,观察者的默认状态应该是这样的: 视图矩阵程序(LookAtTriangles.js) 实际上&…...
 方法)
Python 3 – 文件 readline() 方法
Python 3 – 文件 readline() 方法|极客笔记 # 打开文件 file open("example.txt", "r")# 读取文件中的一行数据 line file.readline() while line:# 移除行尾的换行符print(line.strip())# 读取文件中的下一行数据line file.readline()# 关闭文件 file…...
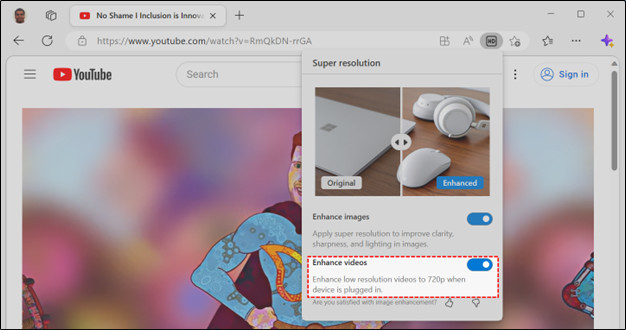
如何在微软Edge浏览器上一键观看高清视频?
编者按:视频是当下最流行的媒体形式之一。但由于视频压缩、网络不稳定等原因,我们常常可以看到互联网上的很多视频其画面质量并不理想,尤其是在浏览器端,这极大地影响了观看体验。不过,近期微软 Edge 浏览器推出了一项…...

Telegram BoT的主流项目盘点
目录 DeFi 类 数据分析类 空投埋伏交易 其他 Telegram Bot赛道的发展趋势预测 Telegram BoT赛道发展较快,具体来看可以分为DeFi 类、数据分析类、空投埋伏交易类以及其他。 DeFi 类 Unibot(交易)、Banana Gun、WagieBot(交…...

PTA 甲级 1044 Shopping in Mars
题目链接 思路:前缀和滑动窗口 #include<bits/stdc.h> #define MAXN 100010 using namespace std; int a[MAXN];int main(){int n,m;cin>>n>>m;//n数量 m金额for(int i1;i<n;i){int t;cin>>t;a[i]a[i-1]t;//前缀和}vector<pair<in…...

Linux学习之MyCat实现分库分表
环境准备 先准备一套MySQL主从服务器,可参考MySQL主从配置配置MyCat服务 资源下载 网盘链接: https://pan.baidu.com/s/1cLTMH_e1-6loc_gF9ZNHTg?pwda63n 提取码: a63n MyCat配置 # 1)安装mycat软件 //安装jdk [rootmycat58 upload]# yum -y insta…...

DirectX12(d3d12)初始化
一、前置要求 Windows 10及以上(安装有DirectX12)VisualStudio 2022 二、DirectX12入门 1.引用头文件 #include<Windows.h> #include<d3d12.h> #include<dxgi1_4.h>2.注册窗口类并初始化窗口 这里我们调用Windows API 通过应用程序的句柄来注册一个唯一…...

算法通关村-----回溯模板如何解决排列组合问题
组合总和 问题描述 给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限…...
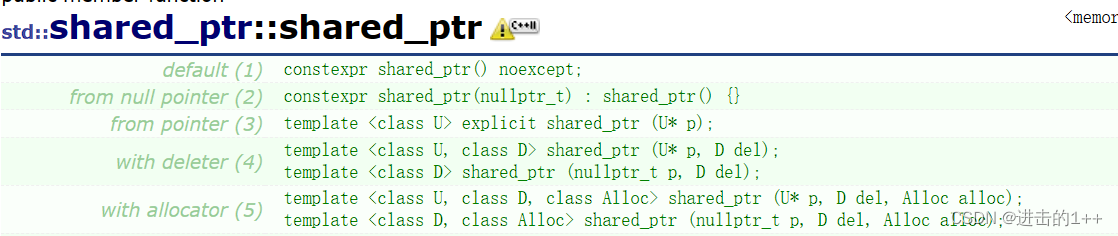
【1++的C++进阶】之智能指针
👍作者主页:进击的1 🤩 专栏链接:【1的C进阶】 文章目录 一,什么是智能指针二,为什么需要智能指针三,智能指针的发展 一,什么是智能指针 要了解智能指针,我们先要了解RA…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...
