Java手写最短路径算法和案例拓展
Java手写最短路径算法和案例拓展
1. 算法手写的必要性
在实际开发中,经常需要处理图的最短路径问题。虽然Java提供了一些图算法库,但手写最短路径算法的必要性体现在以下几个方面:
- 理解算法原理:手写算法可以帮助我们深入理解最短路径算法的原理和思路,提高对算法的理解程度。
- 灵活性和可定制性:手写算法可以根据具体需求进行定制,满足不同场景下的需求。
- 性能优化:手写算法可以根据具体情况进行性能优化,提高算法的效率。
2. 市场调查
在市场调查中,我们发现最短路径算法在物流、导航、网络通信等领域有着广泛的应用。例如,物流公司需要确定最短路径来优化运输成本;导航软件需要找到最短路径来指导用户行驶;网络通信需要确定最短路径来提高数据传输效率。
3. 实现思路原理
为了更好地理解最短路径算法的实现思路,我们使用Mermanid代码表示思维导图,解释实现思路的原理。
上述思维导图描述了最短路径算法的基本思路:从起点开始,逐步选择下一个顶点,并更新距离和路径,直到到达目标顶点,输出最短路径。
4. 实现的详细介绍和详细步骤
步骤1:初始化距离和路径
在开始算法之前,需要初始化距离和路径。距离表示从起点到每个顶点的最短距离,路径表示从起点到每个顶点的最短路径。
// 初始化距离和路径
for (int i = 0; i < vertexCount; i++) {distance[i] = Integer.MAX_VALUE;path[i] = -1;
}
distance[start] = 0;
步骤2:选择起点
选择起点作为当前顶点,并标记为已访问。
int current = start;
visited[current] = true;
步骤3:更新距离和路径
遍历当前顶点的所有邻接顶点,更新距离和路径。
for (int neighbor : getNeighbors(current)) {if (!visited[neighbor]) {int newDistance = distance[current] + getWeight(current, neighbor);if (newDistance < distance[neighbor]) {distance[neighbor] = newDistance;path[neighbor] = current;}}
}
步骤4:选择下一个顶点
从未访问的顶点中选择距离最小的顶点作为下一个顶点。
int minDistance = Integer.MAX_VALUE;
for (int i = 0; i < vertexCount; i++) {if (!visited[i] && distance[i] < minDistance) {minDistance = distance[i];current = i;}
}
visited[current] = true;
步骤5:重复选择下一个顶点
重复步骤3和步骤4,直到所有顶点都被访问。
步骤6:输出最短路径
根据路径数组,输出从起点到目标顶点的最短路径。
List<Integer> shortestPath = new ArrayList<>();
int vertex = target;
while (vertex != -1) {shortestPath.add(vertex);vertex = path[vertex];
}
Collections.reverse(shortestPath);
5. 手写实现总结及必要性
通过手写最短路径算法的实现,我们深入理解了算法的原理和思路。手写实现能够提高我们对算法的理解程度,并且具有灵活性和可定制性,可以根据具体需求进行定制和性能优化。手写最短路径算法在物流、导航、网络通信等领域有着广泛的应用前景。
5.1 手写完整代码
以下是一个使用Dijkstra算法求解最短路径的完整代码示例:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.List;public class DijkstraAlgorithm {private int vertexCount;private int[][] adjacencyMatrix;public DijkstraAlgorithm(int vertexCount) {this.vertexCount = vertexCount;adjacencyMatrix = new int[vertexCount][vertexCount];}public void addEdge(int source, int destination, int weight) {adjacencyMatrix[source][destination] = weight;adjacencyMatrix[destination][source] = weight;}public List<Integer> shortestPath(int start, int target) {int[] distance = new int[vertexCount];int[] path = new int[vertexCount];boolean[] visited = new boolean[vertexCount];// 初始化距离和路径Arrays.fill(distance, Integer.MAX_VALUE);Arrays.fill(path, -1);distance[start] = 0;// 选择起点int current = start;visited[current] = true;// 更新距离和路径for (int neighbor = 0; neighbor < vertexCount; neighbor++) {if (!visited[neighbor] && adjacencyMatrix[current][neighbor] > 0) {int newDistance = distance[current] + adjacencyMatrix[current][neighbor];if (newDistance < distance[neighbor]) {distance[neighbor] = newDistance;path[neighbor] = current;}}}// 选择下一个顶点for (int i = 1; i < vertexCount; i++) {int minDistance = Integer.MAX_VALUE;for (int j = 0; j < vertexCount; j++) {if (!visited[j] && distance[j] < minDistance) {minDistance = distance[j];current = j;}}visited[current] = true;// 更新距离和路径for (int neighbor = 0; neighbor < vertexCount; neighbor++) {if (!visited[neighbor] && adjacencyMatrix[current][neighbor] > 0) {int newDistance = distance[current] + adjacencyMatrix[current][neighbor];if (newDistance < distance[neighbor]) {distance[neighbor] = newDistance;path[neighbor] = current;}}}}// 输出最短路径List<Integer> shortestPath = new ArrayList<>();int vertex = target;while (vertex != -1) {shortestPath.add(vertex);vertex = path[vertex];}Collections.reverse(shortestPath);return shortestPath;}public static void main(String[] args) {DijkstraAlgorithm graph = new DijkstraAlgorithm(6);graph.addEdge(0, 1, 2);graph.addEdge(0, 2, 4);graph.addEdge(1, 2, 1);graph.addEdge(1, 3, 7);graph.addEdge(2, 4, 3);graph.addEdge(3, 4, 1);graph.addEdge(3, 5, 5);graph.addEdge(4, 5, 2);List<Integer> shortestPath = graph.shortestPath(0, 5);System.out.println("Shortest Path: " + shortestPath);}
}
以上代码实现了一个Dijkstra算法的最短路径求解器。在示例中,我们创建了一个有6个顶点的图,并添加了8条边。然后,我们使用Dijkstra算法计算从顶点0到顶点5的最短路径,并打印出结果。输出结果为Shortest Path: [0, 2, 4, 5],表示从顶点0到顶点5的最短路径为0 -> 2 -> 4 -> 5。
6. 拓展案例
下面是一个拓展案例,展示了每个步骤的代码进行文字描述:
// 步骤1:初始化距离和路径
for (int i = 0; i < vertexCount; i++) {distance[i] = Integer.MAX_VALUE;path[i] = -1;
}
distance[start] = 0;// 步骤2:选择起点
int current = start;
visited[current] = true;// 步骤3:更新距离和路径
for (int neighbor : getNeighbors(current)) {if (!visited[neighbor]) {int newDistance = distance[current] + getWeight(current, neighbor);if (newDistance < distance[neighbor]) {distance[neighbor] = newDistance;path[neighbor] = current;}}
}// 步骤4:选择下一个顶点
int minDistance = Integer.MAX_VALUE;
for (int i = 0; i < vertexCount; i++) {if (!visited[i] && distance[i] < minDistance) {minDistance = distance[i];current = i;}
}
visited[current] = true;// 步骤5:重复选择下一个顶点// 步骤6:输出最短路径
List<Integer> shortestPath = new ArrayList<>();
int vertex = target;
while (vertex != -1) {shortestPath.add(vertex);vertex = path[vertex];
}
Collections.reverse(shortestPath);
通过以上拓展案例,我们可以更加清晰地了解每个步骤的代码实现和作用。
相关文章:

Java手写最短路径算法和案例拓展
Java手写最短路径算法和案例拓展 1. 算法手写的必要性 在实际开发中,经常需要处理图的最短路径问题。虽然Java提供了一些图算法库,但手写最短路径算法的必要性体现在以下几个方面: 理解算法原理:手写算法可以帮助我们深入理解最…...

深度学习实战51-基于Stable Diffusion模型的图像生成原理详解与项目实战
大家好,我是微学AI,今天给大家介绍一下深度学习实战51-基于Stable Diffusion模型的图像生成原理详解与项目实战。大家知道现在各个平台发的漂亮小姐姐,漂亮的图片是怎么生成的吗?这些生成的底层原理就是用到了Stable Diffusion模型。Stable Diffusion是一种基于深度学习的图…...
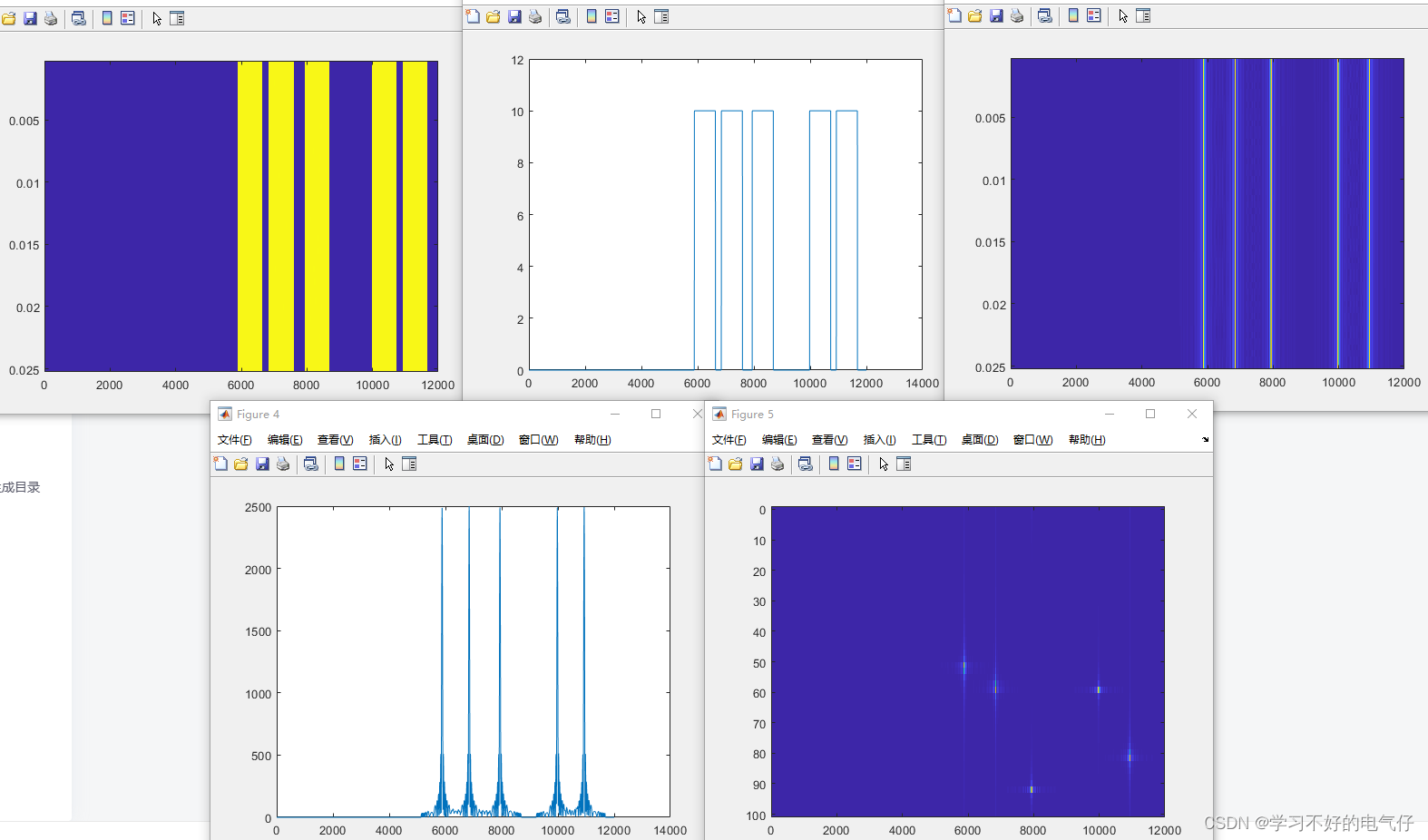
基于matlab实现的多普勒脉冲雷达回波仿真
完整程序: clear all;clc;close all; fc3e9; %载波频率 PRF2000; Br5e6; %带宽 fs10*Br; %采样频率 Tp5e-6; %脉宽 KrBr/Tp; %频率变化率 c3e8; %光速 lamda…...

Linux服务器中安装Anaconda+Tensorflow+Keras
Anaconda安装 从https://repo.anaconda.com/archive/查看你需要下载的Anaconda版本,例如2020.11的x86_64(uname -a 查看linux框架)版下载Anaconda到linux服务器, wget https://repo.anaconda.com/archive/Anaconda3-2020.11-Li…...

ubuntu+.net6+docker 应用部署教程
先期工作 1、本地首先安装 Docker Desktop 2、本地装linux in windows 3、生成镜像 后期工作 1、云服务器部署 生成镜像方法 1、生成Dockerfile配置文件 开发工具visual studio 2022 如果项目已经存在,可以选中项目,右键点击->选择添加Docker…...

Spring常见面试题总结
什么是Spring Spring是一个轻量级Java开发框架,目的是为了解决企业级应用开发的业务逻辑层和其他各层的耦合问题,以提高开发效率。它是一个分层的JavaSE/JavaEE full-stack(一站式)轻量级开源框架,为开发Java应用程序…...
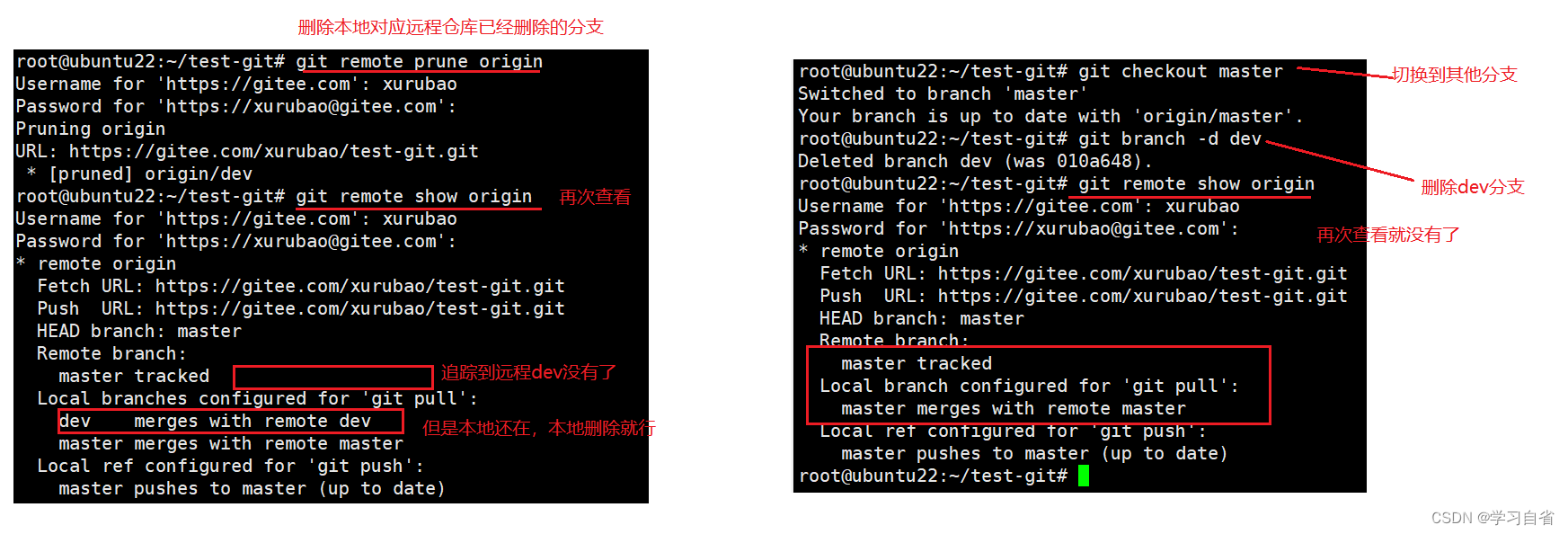
Git全套命令使用
日升时奋斗,日落时自省 目录 1、Git安装 1.1、创建git本地仓库 1.2、配置Git 1.3、认识Git内部区分 2、Git应用操作 2.1、添加文件 2.2、查看日志 2.3、查看修改信息 2.4、查看添加信息 3、版本回退 4、撤销修改 4.1、工作区撤销 4.2、已经add…...
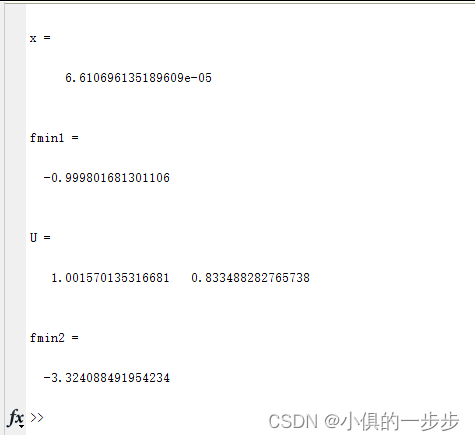
【陕西理工大学-数学软件实训】数学实验报告(8)(数值微积分与方程数值求解)
目录 一、实验目的 二、实验要求 三、实验内容与结果 四、实验心得 一、实验目的 1. 掌握求数值导数和数值积分的方法。 2. 掌握代数方程数值求解的方法。 3. 掌握常微分方程数值求解的方法。 二、实验要求 1. 根据实验内容,编写相应的MATLAB程序,…...

Vue3为什么推荐使用ref而不是reactive
为什么推荐使用ref而不是reactive reactive本身具有很大局限性导致使用过程需要额外注意,如果忽视这些问题将对开发造成不小的麻烦;ref更像是vue2时代option api的data的替代,可以存放任何数据类型,而reactive声明的数据类型只能是对象; 先抛出结论,再详细说原因:非必要不用rea…...

JavaScript函数this指向
一、this的指向规则 1.this到底指向什么呢? 我们先来看一个让人困惑的问题: 定义一个函数,我们采用三种不同的方式对它进行调用,它产生了三种不同的结果 // 定义函数 function foo(name) {console.log("foo函数:", …...
Java的序列化
写在前面 本文看下序列化和反序列化相关的内容。 源码 。 1:为什么,什么是序列化和反序列化 Java对象是在jvm的堆中的,而堆其实就是一块内存,如果jvm重启数据将会丢失,当我们希望jvm重启也不要丢失某些对象ÿ…...
)
计算机二级python简单应用题刷题笔记(一)
计算机二级python简单应用题刷题笔记(一) 1、词频统计:键盘输入一组我国高校所对应的学校类型,以空格分隔,共一行。2、找最大值、最小值、平均分:键盘输入小明学习的课程名称及考分等信息,信息间…...

Spring注解家族介绍: @RequestMapping
前言: 今天我们来介绍RequestMapping这个注解,这个注解的内容相对来讲比较少,篇幅会比较短。 目录 前言: RequestMapping 应用场景: 总结: RequestMapping RequestMapping 是一个用于映射 HTTP 请求…...

系统架构设计师(第二版)学习笔记----信息安全系统及信息安全技术
【原文链接】系统架构设计师(第二版)学习笔记----信息加解密技术 文章目录 一、信息安全系统的组成框架1.1 信息安全系统组成框架1.2 信息安全系统技术内容1.3 常用的基础安全设备1.4 网络安全技术内容1.5 操作系统安全内容1.6 操作系统安全机制1.7 数据…...

交换机的工作原理(含实例,华为ensp操作)
目录 1.交换机学习和转发 案例 1.设置静态地址表项 2.配置黑洞mac地址表项 1.交换机学习和转发 交换机工作在数据链路层。当交换机从某个端口收到一个帧时,它并不是向所有的接口转发此帧,而是根据此帧的目的MAC地址&a…...
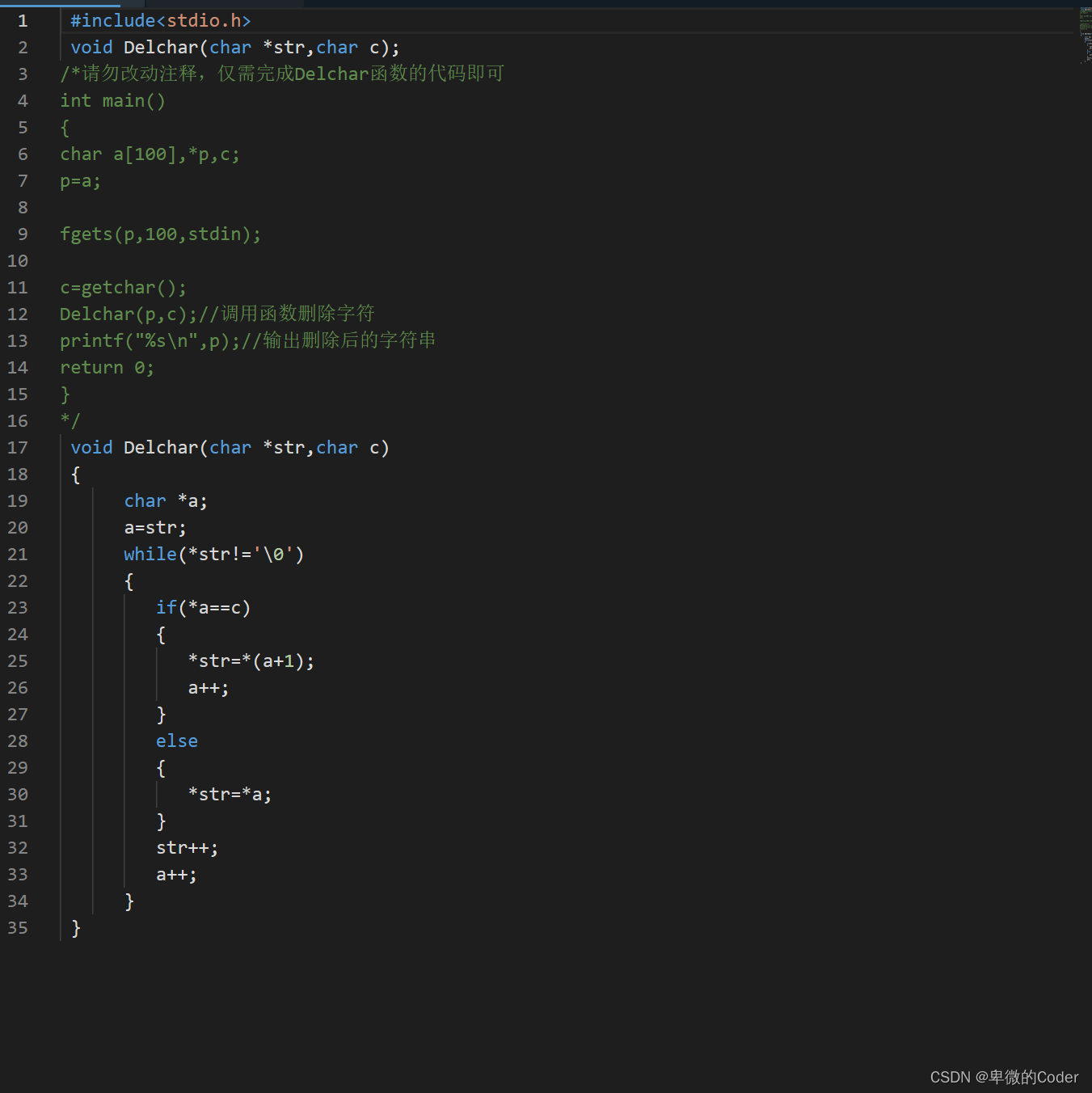
从字符串中删除指定字符
任务描述 编写一个函数实现功能:从字符串中删除指定的字符。同一字母的大、小写按不同字符处理。例如:程序执行时输入字符串:turbo c and Borland c,从键盘输入字符n,则输出后变为:turbo c ad Borlad c。如…...
)
Xcode14.3.1 真机调试iOS17的方法(无iOS17 DeviceSupport)
由于iOS17需要使用Xcode15 才能调试,而当前Xcode15都是beta,正式版还未出,那么要真机调试iOS17的方式一般有两种: 方法一: 一种是下载新的Xcode15 beta版 (但Xcode包一般比较大,好几个G&#…...

JWT基础
概念 JSON Web Token本质上就是一串字符串,一串包含了很多信息的字符串令牌拥有三个部分头部-包含加密算法和令牌类型{"alg":"算法名称","type":"JWT"}负载-包含数据和信息-七个官方默认-也可以自己定义内容{issÿ…...

关于远程工作的面试可能存在的陷阱
附上看到的完整帖子地址:面试 POPER 的后端开发工程师的离奇经历 分享一下我遇到过的,我至少面试过10个远程工作,其中有3个的面试是直接让我完成一个需求的,前两次都耐心做了,第3次看到相同要求时我都懒得回复了&…...
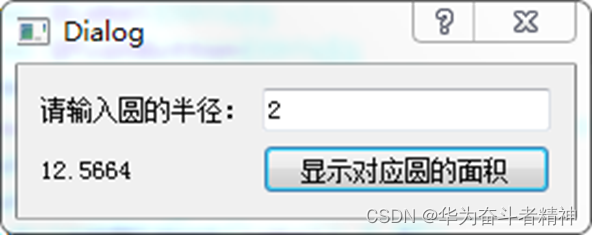
Qt5开发及实例V2.0-第一章Qt概述
Qt5开发及实例V2.0-第一章-Qt概述 第一章-Qt概述1.1 什么是Qt1.2 Qt 5的安装1.2.1 下载安装Qt 51.2.2 运行Qt 5 Creator1.2.3 Qt 5开发环境 1.3 Qt 5开发步骤及实例1.3.1 设计器Qt 5 Designer实现1.3.2 代码实现简单实例 L1.2 Qt 5安装:概念解析L1.3 Qt 5开发步骤及…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
