JS中的数值精度问题(二)
一、精度范围,精度最多只能到53个二进制位
JavaScript 能够准确表示的整数范围在-2^53到2^53之间(不含两个端点),超过这个范围,无法精确表示这个值。
国际标准IEEE 754规定,有效数字第一位默认总是1,不保存在64位浮点数之中。也就是说,有效数字总是1.xxxx的形式,其中xxxx的部分(称为尾数或者有效数字,负责数字的精度)保存在64位浮点数(共52位),最长可能为52位。因此(算上第一位不显示的位),JavaScript提供的有效数字为53个二进制位。
当 e - 1023 = 52,即e = 1075,小数f最大(52位全为1)时,能表示出最大安全正整数,为
1.111...111 * 2^52
52个1
转为十进制值为 2^53−1 = 9007199254740991,则能表示的最小安全负整数为-9007199254740991
整数区间: -(2^53-1) ~ (2^53-1)
Number.MAX_SAFE_INTEGER === Math.pow(2, 53) - 1
// true
Number.MAX_SAFE_INTEGER === 9007199254740991 // Math.pow(2, 53) // 9007199254740992
// true
Number.MIN_SAFE_INTEGER === -Number.MAX_SAFE_INTEGER
// true
Number.MIN_SAFE_INTEGER === -9007199254740991
二、数值范围: [−1.7976931348623157 * 10^308, −5 * 10^−324] ∪ [5* 10^−324, 1.7976931348623157 * 10^308]
最小安全负整数: -(2^53-1) = -9007199254740991
最大安全正整数: 2^53-1 = 9007199254740991
最大数值 Number.MAX_VALUE 属性值接近于 1.79E+308。大于 MAX_VALUE 的值代表 "Infinity";
最小的正值 Number.MIN_VALUE 属性值约为 5e-324,是 JavaScript 里最接近 0 的正值,而不是最小的负值,小于 MIN_VALUE 的值将会转换为0;
64位浮点数的指数部分的长度是11个二进制位,意味着64位浮点数的指数部分的值最大为2047(2的11次方减1),分出一半表示负数,则JavaScript能够表示的数值范围为2^-1023 到 2^1024,超出这个范围的整数无法表示。
在规格化中,当指数e最大(前10位为1,11位为0,即2046)且小数f最大(52位全为1)时,能表示出最大正值,为
1.111...111 * 2^1023
52个1
转化成十进制为 1.7976931348623157 * 10^308,则能表示的最小负值为-1.7976931348623157e+308
Number.MAX_VALUE 属性表示在 JavaScript 里所能表示的最大数值。
如果一个数大于等于2的1024,那么就会发生正同溢出,即JavaScript无法表示这么大的数,这时就会返回Infinity
1.79E308
在非规格化中,当指数e最小(前10位为0,11位为1,即1)且小数f最小(前51位全为0,52位为1)时,能表示出最小正值,为
0.000...01 * 2^-1022 0.000000⋯000001
第52位为1 1073个0
转为十进制值为5e-324,则最大负值为-5e-324
Number.MIN_VALUE 属性表示在 JavaScript 中所能表示的最小的正值
绝对值最接近0的最小正值:如果一个数小于等于2的-1075次方(指数部分最小值-1023,再加上小数部分的52位),那么就会发生为“负向溢出”,即 JavaScript 无法表示这么小的数,这时会直接返回0。
5E-324 === (5 * 10^-324) Math.pow(2, -1075)
IEEE754标准用以下形式来表示一个浮点数:
V = (-1)^s * M * 2^E
符号:(sign)s决定数是负数(s=1)还是正数(s=0)
有效数:(significand)M是一个二进制小数
指数:(exponent)E是2的幂(可能是负数),它的作用是对浮点数加权
64位浮点数: s=1 E=2*11=2048-1=2047
0.1 十进制表示
0.0001100110011001100110011001100110011001100110011001101 二进制表示
[−1.7976931348623157 * 10^308, −5 * 10^−324] ∪ [5* 10^−324, 1.7976931348623157 * 10^308]
超过1.7976931348623157E+308为Infinity,小于-1.7976931348623157E+308为-Infinity,在(-5E-324,5E-324)之间的数显示为0
参考资料:
IEEE-754 64位双精度浮点数存储详解_ieee754双精度浮点数-CSDN博客
ES6 入门教程
浅析浮点数精度问题 - 知乎
相关文章:
)
JS中的数值精度问题(二)
一、精度范围,精度最多只能到53个二进制位 JavaScript 能够准确表示的整数范围在-2^53到2^53之间(不含两个端点),超过这个范围,无法精确表示这个值。 国际标准IEEE 754规定,有效数字第一位默认总是…...

WPF——Control与Template理解
文章目录 一、前言二、控件三、模板3.1 DataTemplate3.2 ControlTemplate3.3 ContentPresenter 四、结语 一、前言 最近又翻看了下刘铁猛的《深入浅出WPF》,发现对模板章节中的部分内容有了更深的体会,所以写篇文扯扯。 文章标题是Control与Template&a…...
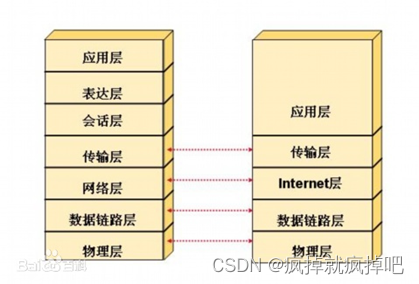
华为HCIA学习(一)
文章目录 一.根据考试题总结知识点(一题一点)二.上午学习三.下午学习四.今天只做了70题,需要的可以找我 一.根据考试题总结知识点(一题一点) 二.上午学习 ① VRP系统是VRP是华为公司从低端到高端的全系列路由器、交换…...
使用jmeter+ant+jenkins+git搭建自动化测试平台
最近正在学习自动化测试,于是随手搭建了一下jmeterantjenkinsgit平台。 接下来,我会按照jdk,jmeter,ant,jenkins,git这个顺序一步一步的搭建起来。 一、jdk。这个就不多说了。我用的是1.8版本的,配环境变…...

C# Winform中在DataGridView中添加Button按钮,操作Button按钮
.Net的DataGridView控件中,提供了一种列的类型,叫 DataGridViewButtonColumn ,这种列类型是展示为一个 按钮,可以给button赋予相应的text,并且,此button可以用来做处理事件的判断依据。 DataGridViewButto…...
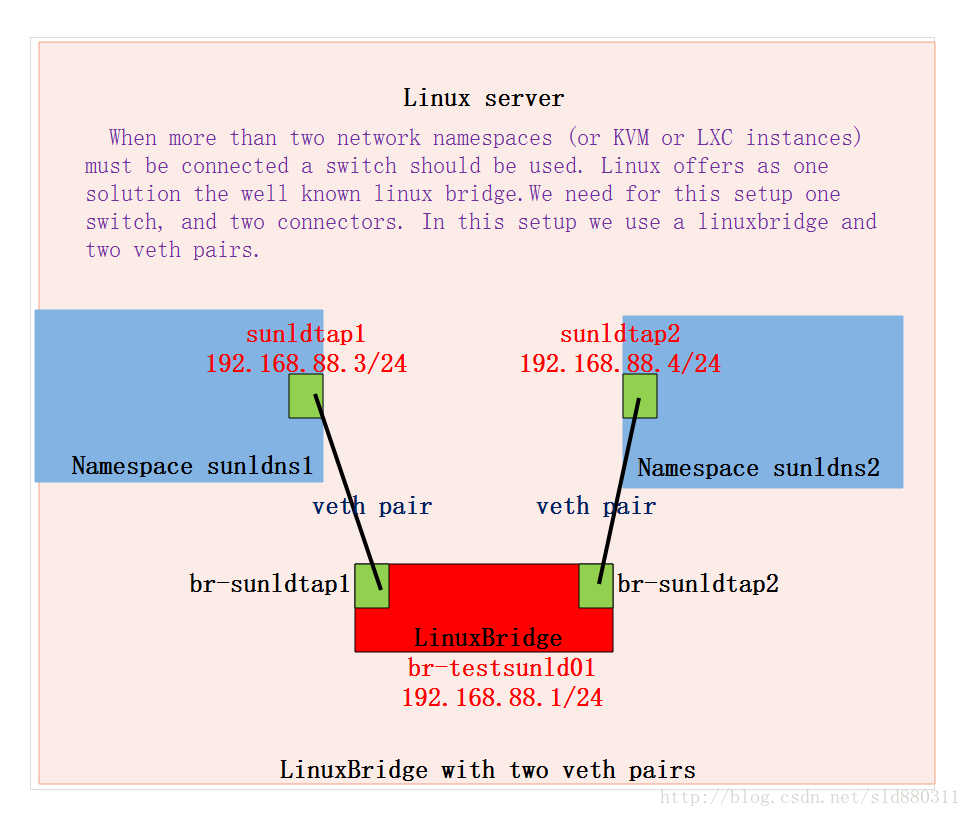
Docker 网络学习
docker的网络模式 当你开始大规模使用Docker时,你会发现需要了解很多关于网络的知识。Docker作为目前最火的轻量级容器技术,有很多令人称道的功能,如Docker的镜像管理。然而,Docker同样有着很多不完善的地方,网络方面…...
django创建web服务器
安装 pip install django 创建项目 django-admin startproject report django-admin startapp data //project下可创建多个app 执行使用 python manage.py migrate //orm代码到数据库 python manage.py runserver 0.0.0.0:80 权限管理 python manage.py createsuperuser 创建…...
极光笔记 | 推送服务数据中心选择:合规性与传输效率的双重考量
随着全球化进程的深入,跨境数据传输与存储问题已经变得愈发重要。推送服务的数据中心节点选择不仅关乎数据访问速度和用户体验,同时也直接牵扯到数据合规性和安全保障。EngageLab Push深知这一点,为了满足更多国际客户和全球用户触达需求&…...

Python灰帽编程——初识Python上
1. Python 简介 常用安全工具语言示例perljoomscan whatwebrubymetasploit-frameworkpythonsqlmap pocsuite3gogoby 1.1 Python 起源 1.1.1 语言的作者 贵铎范罗萨姆(Guido van Rossum)荷兰人于1989 年圣诞节始创了python。 大神就是大神࿰…...

OLED透明屏交互技术:开创未来科技的新篇章
OLED透明屏交互技术作为一项前沿的科技创新,正在以其高透明度、触摸和手势交互等特点,引领着未来科技的发展。 不仅在智能手机、可穿戴设备和汽车行业有着广泛应用,还在广告和展示领域展现出巨大的潜力。 那么,尼伽在这篇文章中将…...

揭秘Spring Boot内嵌Tomcat原理
tomcat 介绍 tomcat 是 web容器(servlet 容器),不管请求是访问静态资源HTML、JSP还是java接口,对tomcat而言,都是通过servlet访问: 访问静态资源,tomcat 会交由一个叫做DefaultServlet的类来处…...
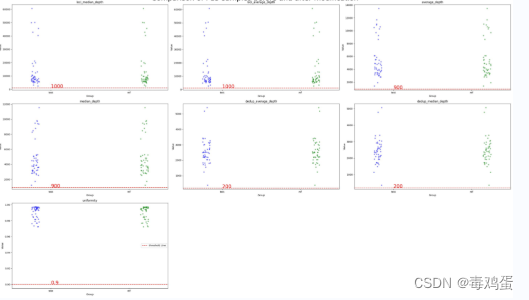
分类散点图 stripplot() 加辅助线axhline() 多图合一
分类散点图 stripplot 加辅助线axhline 多图合一 效果图代码 画图没有什么可说的,直接上图 效果图 代码 # 绘制图, 查看是否数值在阈值上 plt.figure(figsize(30, 18)) n 0 for header, value_list in info_dict.items():ref_value_list ref_info_dic…...
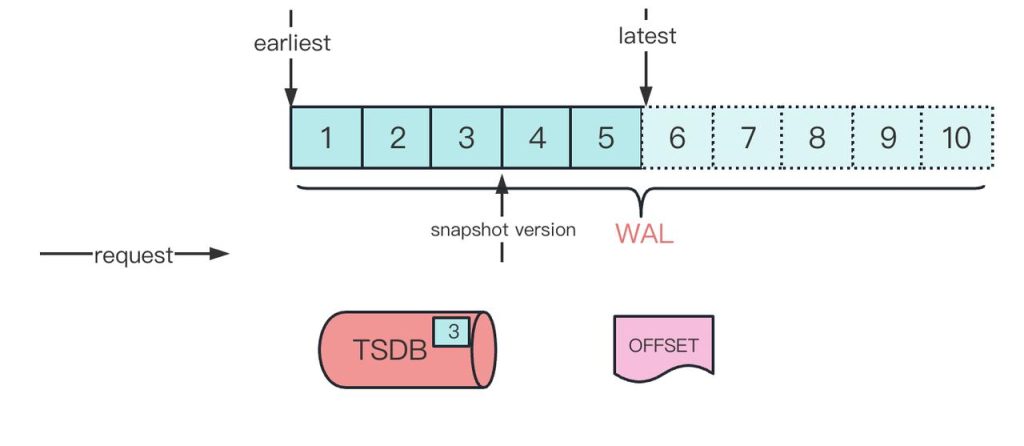
一文告诉你为什么时序场景下 TDengine 数据订阅比 Kafka 好
在 TDengine 3.0 中,我们对流式计算、数据订阅功能都进行了再升级,帮助用户极大简化了数据架构的复杂程度,降低整体运维成本。TDengine 提供的类似消息队列产品的数据订阅、消费接口,本质上是为了帮助应用实时获取写入 TDengine 的…...
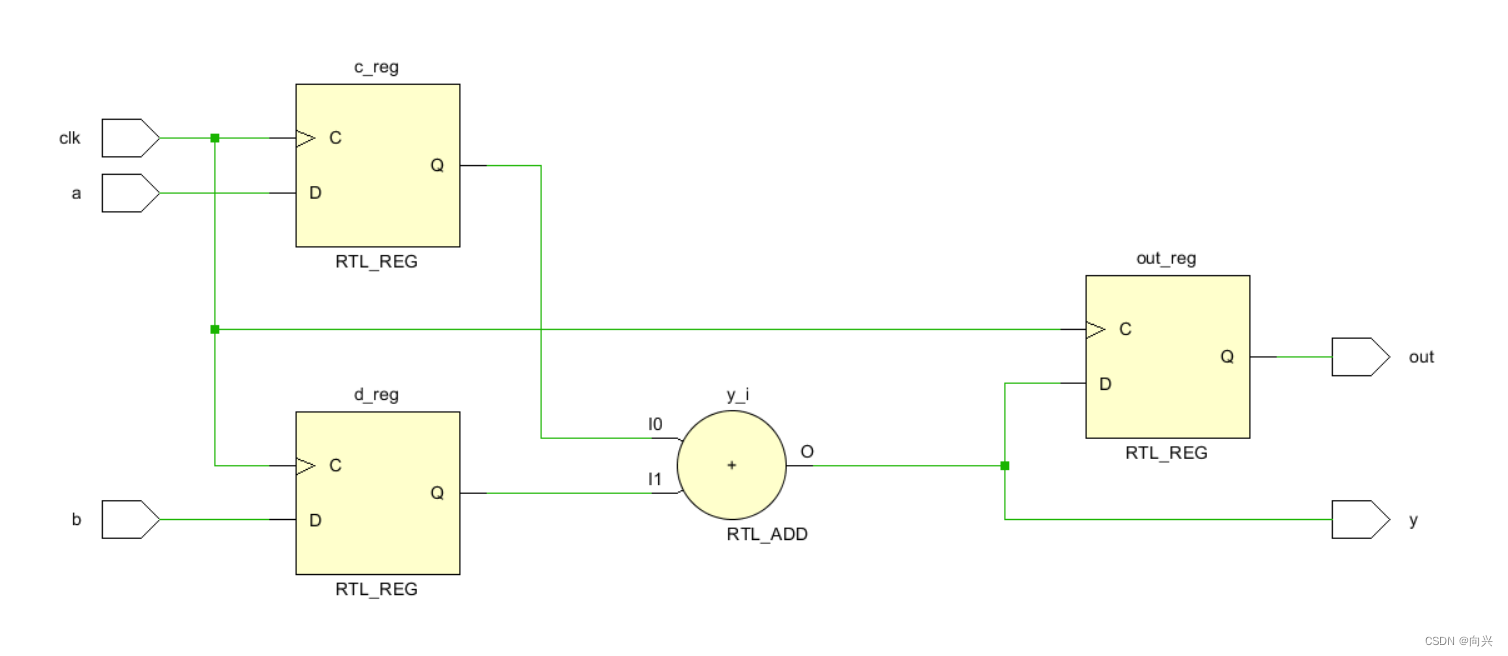
reg与wire的用法,证明reg可以在右边,wire型在左边,来作组合逻辑处理。
reg与wire的用法,证明reg可以在右边,wire型在左边,来作组合逻辑处理。 1,RTL2,生成的原理图 1,RTL 参考文献: 1,verilog 中 wire 和reg 的使用 2,解决一个assign问题&…...
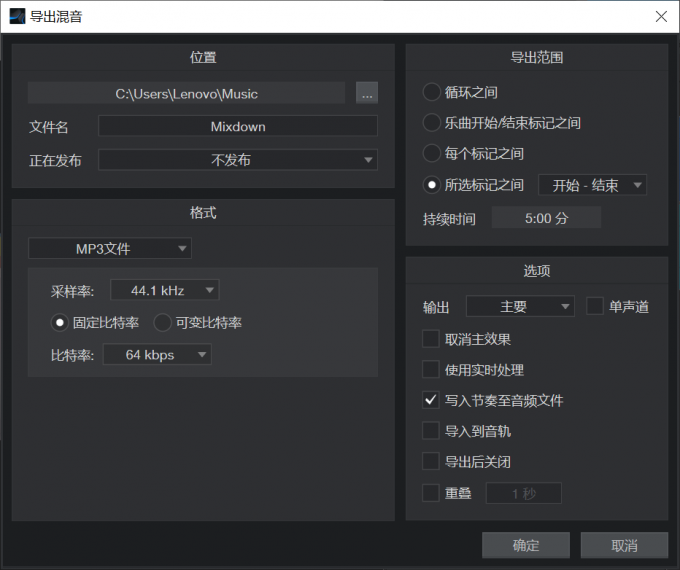
Studio One6.2简体中文免费最新版本宿主软件
对于一些有创作需求的朋友来说,为自己写的歌制作伴奏是很平常的。今天要和大家分享的就是自己写的歌怎么做伴奏,自己做伴奏的软件有哪些。Studio One是宿主软件界的一个后起之秀,推出的时间不久,但是受到了大量音乐制作人的推崇。…...
算法刷题 week2
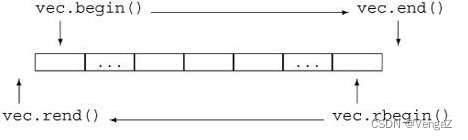
目录 week21. 二维数组中的查找题目题解(单调性扫描) O(nm) 2.替换空格题目题解(线性扫描) O(n)(双指针扫描) O(n) 3.从尾到头打印链表题目题解(遍历链表) O(n) week2 1. 二维数组中的查找 题目 题解 (单调性扫描) O(nm) 核心在于发现每个子矩阵右上角的数的性质࿱…...

子网的划分
强化计算机网络发现王道没有这一块的内容,导致做题稀里糊涂。于是个人调研补充。 子网划分是将一个大型IP网络划分成更小的子网,以实现更有效的网络管理和资源分配。 原因: 提高网络性能:子网划分可以减少广播域的大小ÿ…...

Docker安装与卸载
Docker安装与卸载 安装 yum install -y yum-utils \device-mapper-persistent-data \lvm2 --skip-broken更新本地镜像源 打开终端或 SSH 连接到 Rocky Linux 的服务器。 进入 /etc/yum.repos.d/ 目录,该目录包含 Rocky Linux 的 yum 配置文件。 cd /etc/yum.repo…...
【Davinci开发】:开发过程问题记录及总结
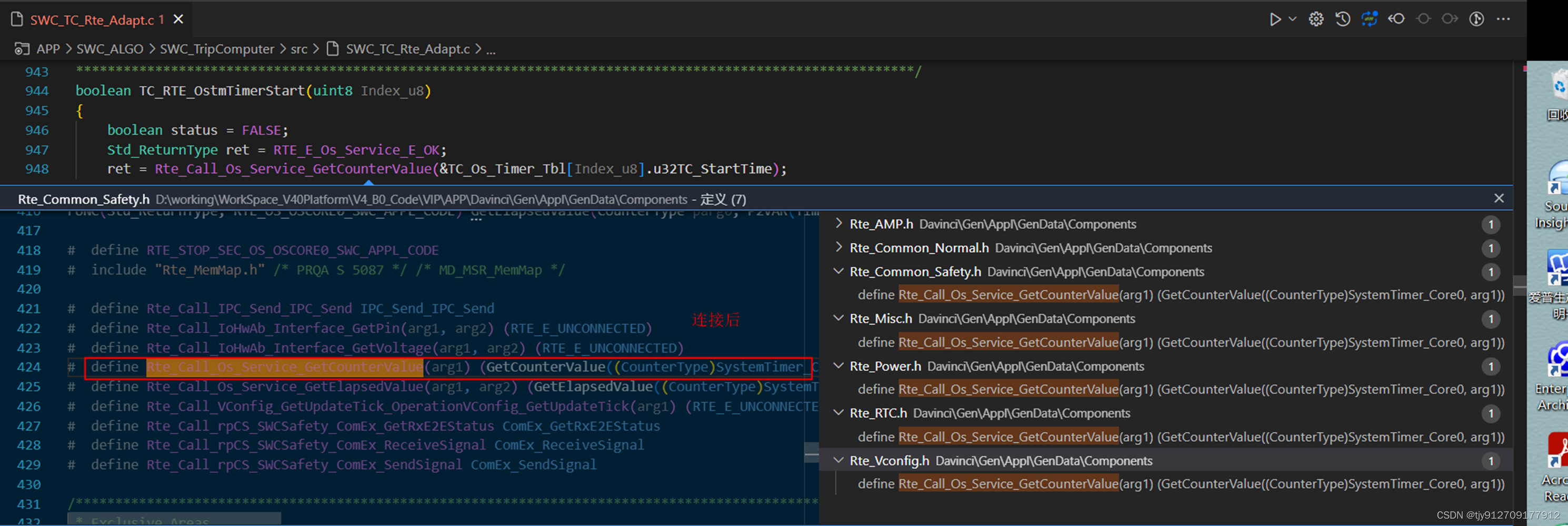
开发过程问题总结 1、SWC访问系统OS Timer返回值异常a、代码发现,RTE接口为未连接状态b、连接后,仍然有问题,单步调试,发现没有访问权限当新平台基于之前平台的代码而延续开发时(应用代码相同,但是芯片已经更换),记录开发过程中遇所到的问题,单步调试,逐一排查。 1、…...
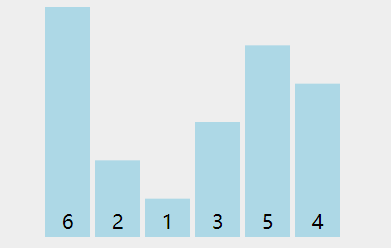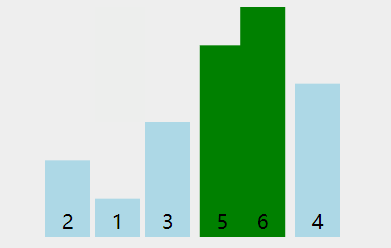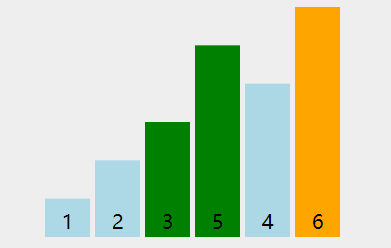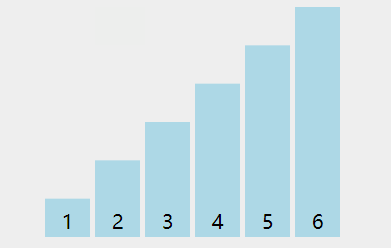
数据结构——排序算法——冒泡排序
冒泡排序1 void swap(vector<int> arr, int i, int j) {int temp arr[i];arr[i] arr[j];arr[j] temp;}void bubbleSort1(vector<int> arr) {for (int i 0; i < arr.size() - 1; i){for (int j 0; j < arr.size() - 1 - i; j){if (arr[j] > arr[j 1…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...

python打卡第47天
昨天代码中注意力热图的部分顺移至今天 知识点回顾: 热力图 作业:对比不同卷积层热图可视化的结果 def visualize_attention_map(model, test_loader, device, class_names, num_samples3):"""可视化模型的注意力热力图,展示模…...
