当前位置： 首页 > news >正文

解决nomachine扫描不出ip问题

news 2026/2/8 14:53:48

IP扫描工具Advanced IP Scanner
快速的扫描局域网中存在ip地址以及pc机的活跃状态，还能列出局域网计算机的相关信息。并且ip扫描工具(Advanced IP Scanner)还能够单击访问更多有用的功能- 远程关机和唤醒
软件下载地址

相关文章：

解决nomachine扫描不出ip问题

IP扫描工具Advanced IP Scanner 快速的扫描局域网中存在ip地址以及pc机的活跃状态，还能列出局域网计算机的相关信息。并且ip扫描工具(Advanced IP Scanner)还能够单击访问更多有用的功能- 远程关机和唤醒 软件下载地址...

编程日记 2023/9/19 21:26:56

Web 3.0 发展到什么水平了？

最初，有互联网：电线和服务器的物理基础设施，让计算机和它们前面的人相互交谈。美国政府的阿帕网在1969年发出了第一条消息，但我们今天所知道的网络直到1991年才出现，当时HTML和URL使用户可以在静态页面之间导航。将此视…...

编程日记 2023/9/19 21:25:54

大模型：如何利用旧的tokenizer训练出一个新的来？

背景： 我们在用chatGPT或者SD的时候，发现如果使用英语写提示词得到的结果比我们使用中文得到的结果要好很多，为什么呢？这其中就有一个叫做tokenizer的东西在作怪。 训练一个合适的tokenizer是训练大模型的基础，我们既…...

编程日记 2023/9/19 21:21:51

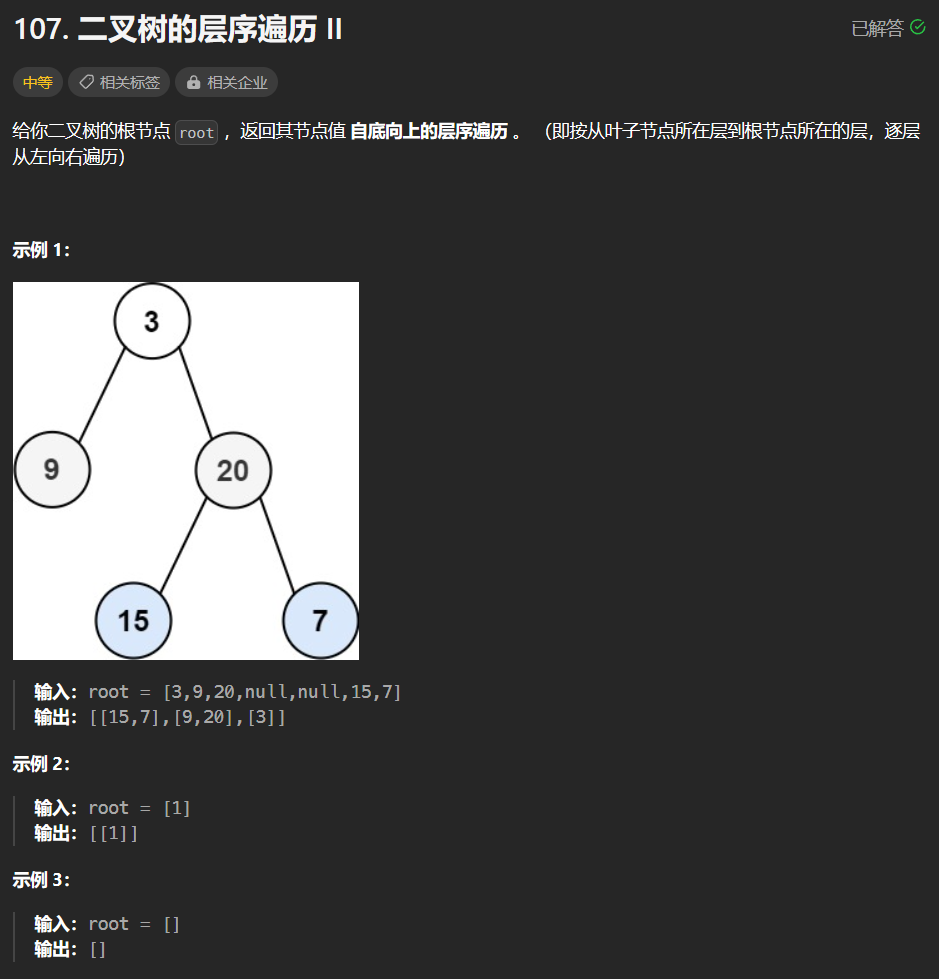
【LeetCode-中等题】107. 二叉树的层序遍历 II

文章目录 题目方法一：队列层序迭代 题目 方法一：队列层序迭代 解题详情：【LeetCode-中等题】102. 二叉树的层序遍历 res.add(0,zres); //效果是将 zres 列表作为 res 的第一个子列表，并将其它原本在第一位置及之后的子列表向后移…...

编程日记 2023/9/19 21:19:48

斯坦福联合培养博士|专科生的逆袭之路

从山东医学高等专科学校到首都医科大学附属北京天坛医院神经外科博士，再到斯坦福医学院神经外科联合培养博士，知识人网小编带大家看看何世豪通往成功的逆袭之路。 上面照片中这位戴眼镜的主人公就是何志豪，他从山东医学高等专科学校考入泰山医…...

编程日记 2023/9/19 21:18:47

Verilog中parameter在仿真时的应用

parameter能够定义一个常量 例如 parameter [7:0]A 8d123; 在仿真时我们可以用它来改变模块的参数，而不会影响综合的结果。 考虑下面的模块，输入时钟是clk，频率为24MHz，输出一个1Hz的方波驱动小灯让其闪烁 module test1(in…...

编程日记 2023/9/19 21:17:46

v-model绑定导致的element UI文本框输入第一次值后被绑定，导致空文本框无法再输入文字

在工作岗位上，上边分配一个任务，创建一个页面，从0-1，全部自己搭建，也没有啥模版，就这么来，那就直接来吧，没办法，那就直接上手，开发过程中，我使用了…...

编程日记 2023/9/19 21:12:41

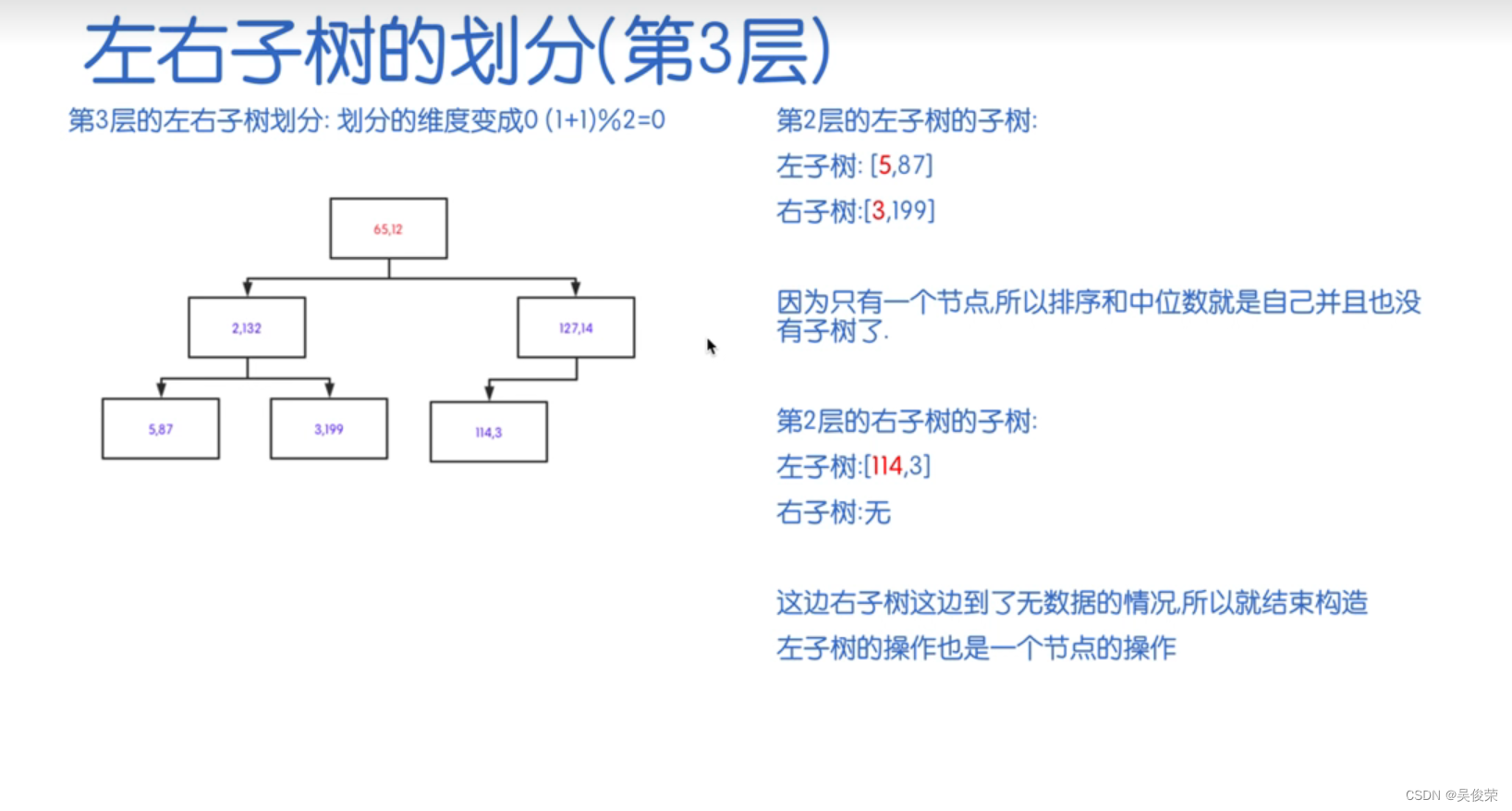
数据结构——KD树

KD树（K-Dimensional Tree）是一种用于多维空间的二叉树数据结构，旨在提供高效的数据检索。KD树在空间搜索和最近邻搜索等问题中特别有用，允许在高维空间中有效地搜索数据点。 重要性质 1.分割K维数据空间的数据结构 2.是一颗二叉树…...

编程日记 2023/9/19 21:10:39

python趣味编程-恐龙克隆游戏

Python 中使用 Turtle 的恐龙克隆游戏免费源代码 使用 Turtle 的恐龙克隆游戏是一个用Python编程语言编码的桌面游戏应用程序。该项目包含在 Chrome 浏览器中克隆实际恐龙游戏的多种功能。该项目可以使正在修读 IT 相关课程的学生受益。这个应用程序非常有趣，可以帮助您学习创…...

编程日记 2023/9/19 21:08:37

【漏洞复现】泛微e-office OfficeServer2.php 存在任意文件读取漏洞复现

文章目录 前言声明一、漏洞描述二、漏洞分析三、漏洞复现四、修复建议前言 泛微e-office OfficeServer2.php 存在任意文件读取漏洞，攻击者可通过构造特定Payload获取敏感数据信息。 声明 请勿利用文章内的相关技术从事非法测试，由于传播、利用此文所提供的信息或者工具而造…...

编程日记 2023/9/19 21:07:37

基于Yolov8的野外烟雾检测（4）：通道优先卷积注意力（CPCA），效果秒杀CBAM和SE等 | 中科院2023最新发表

目录 1.Yolov8介绍 2.野外火灾烟雾数据集介绍 3.CPCA介绍 3.1 CPCA加入到yolov8 4.训练结果分析 5.系列篇 1.Yolov8介绍 Ultralytics YOLOv8是Ultralytics公司开发的YOLO目标检测和图像分割模型的最新版本。YOLOv8是一种尖端的、最先进的（SOTA）模型&a…...

编程日记 2023/9/19 21:04:34

程序员必掌握的核心算法：提升编程技能的关键路径

一：引言 作为程序员，算法是我们编程生涯中的灵魂。算法是解决问题的方法和步骤，它们在计算机科学中扮演着至关重要的角色。无论你是初学者还是经验丰富的专业人士，都需要掌握一些核心算法，因为它们在各种应用场景中频…...

编程日记 2023/9/19 21:01:30

面试算法10：和为k的子数组

题目 输入一个整数数组和一个整数k，请问数组中有多少个数字之和等于k的连续子数组？例如，输入数组[1，1，1]，k的值为2，有2个连续子数组之和等于2。 分析 在从头到尾逐个扫描数组中的数字时求出前…...

编程日记 2023/9/19 21:00:29

王道考研操作系统

王道考研操作系统 计算机系统概述操作系统的概念操作系统的特征操作系统的发展历程操作系统内核中断和异常![在这里插入图片描述](https://img-blog.csdnimg.cn/162452b4c60144e0bd500e180127c447.png)系统调用操作系统结构虚拟机错题 进程与线程进程控制进程通信线程和多线程模…...

编程日记 2023/9/19 20:55:22

HEXO 基本使用

1 新建、编辑并预览文章 1. 新建文章 hexo new [layout] title # 或 hexo n [layout] title创建文章前要先选定模板，在hexo中也叫做布局。hexo支持三种布局（layout）：post(默认)、draft、page。我们先介绍如何使用已有布局…...

编程日记 2023/9/19 20:53:20

Webpack Sourcemap文件泄露漏洞

Webpack Sourcemap文件泄露漏洞 前言一、Webpack和Sourcemap1.1 什么是Webpack1.2 什么是Sourcemap二、漏洞利用2.1 使用reverse-sourcemap工具2.1 直接看前端代码三、漏洞挖掘漏洞修复前言 Webpack主要是用于前端框架进行打包的工具，打包后形成.js.map文件，如果.js.map文件…...

编程日记 2023/9/19 20:52:19

WebGL层次模型——单节点模型

目录 多个简单模型组成的复杂模型 层次结构模型 单关节模型 JointModel程序中模型的层次结构 示例程序（JointMode.js） 代码详解 绘制层次模型（draw（）） 程序效果 多个简单模型组成的复杂模型 绘制…...

编程日记 2023/9/19 20:51:19

【链表】反转链表 II-力扣 92 题

💝💝💝欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学…...

编程日记 2023/9/19 20:49:16

【考研数学】高等数学第六模块 —— 空间解析几何（1，向量基本概念与运算）

文章目录 引言一、空间解析几何的理论1.1 基本概念1.2 向量的运算 写在最后 引言 我自认空间想象能力较差，所以当初学这个很吃力。希望现在再接触，能好点。 一、空间解析几何的理论 1.1 基本概念 1.向量 —— 既有大小，又有方向的量称为向…...

编程日记 2023/9/19 20:48:15

巨人互动|Facebook海外户Facebook客户反馈分数

Facebook客户反馈分数是一项用于衡量用户对Facebook产品和服务满意度的指标。该指标被广泛应用于各种调研和评估活动，帮助Facebook了解用户对其平台和功能的意见和建议，并从中识别出改进的机会。 巨人互动|Facebook海外户&Facebook新闻提要的算法&am…...

编程日记 2023/9/19 20:46:13

Vim 调用外部命令学习笔记

Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

编程新知 2025/11/16 8:24:16

在软件开发中正确使用MySQL日期时间类型的深度解析

在日常软件开发场景中，时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志，到供应链系统的物流节点时间戳，时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库，其日期时间类型的…...

编程新知 2025/10/16 13:22:06

基于大模型的 UI 自动化系统

基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统，利用大模型实现智能 UI 自动化，结合计算机视觉和自然语言处理技术，实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

编程新知 2025/10/22 11:16:20

CTF show Web 红包题第六弹

提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框，很难让人不联想到SQL注入，但提示都说了不是SQL注入，所以就不往这方面想了 ​ 先查看一下网页源码，发现一段JavaScript代码，有一个关键类ctfs…...

编程新知 2026/2/5 4:33:58

高等数学（下）题型笔记（八）空间解析几何与向量代数

目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

编程新知 2026/1/28 9:04:29

SpringTask-03.入门案例

一.入门案例 启动类： package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

编程新知 2026/2/2 0:35:08

Map相关知识

数据结构 二叉树 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子 节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只 有左子节点，有的节点只有…...

编程新知 2026/2/4 16:21:14

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容

目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法，当前调用一个医疗行业的AI识别算法后返回…...

编程新知 2026/1/20 22:45:38

让回归模型不再被异常值“带跑偏“，MSE和Cauchy损失函数在噪声数据环境下的实战对比

在机器学习的回归分析中，损失函数的选择对模型性能具有决定性影响。均方误差（MSE）作为经典的损失函数，在处理干净数据时表现优异，但在面对包含异常值的噪声数据时，其对大误差的二次惩罚机制往往导致模型参数…...

编程新知 2026/1/28 2:18:46

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变（硬件篇）

本项目是基于 STM32F103C8T6 微控制器的 SPWM（正弦脉宽调制）电源模块，能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路，图中 D1 为二极管， 其目的是防止正负极电源反接， …...

编程新知 2026/1/25 3:29:22